Padéapproximant approach to singular properties of quantum gases:the ideal cases

Yuan-Hong Tian(田远鸿),Wen-Du Li(李文都),Yao Shen(沈尧) and Wu-Sheng Dai(戴伍圣),*

1 Department of Physics,Tianjin University,Tianjin 300350,China

2 College of Physics and Materials Science,Tianjin Normal University,Tianjin 300387,China

3 School of Criminal Investigation and Forensic Science,People’s Public Security University of China,Beijing 100038,China

Abstract In this paper,we show how to recover the low-temperature and high-density information of ideal quantum gases from the high-temperature and low-density approximation by the Padé approximant.The virial expansion is a high-temperature and low-density expansion and in practice,often,only the first several virial coefficients can be obtained.For Bose gases,we determine the BEC phase transition from a truncated virial expansion.For Fermi gases,we recover the low-temperature and high-density result from the virial expansion.

Keywords:approximate analytic continuation,virial expansion,Padéapproximant,quantum gas

1.Introduction

Singularity reflects the global behavior of a function.In perturbation theory,we usually use a truncated power series to approximate a function,i.e.use a polynomial to approximate a function.However,polynomials are entire functions and have no singularities.This means that if we use perturbation theory to approximate a physical quantity,the information of singularity will be lost;that is,even in the perturbation theory the approximation can be made accurate enough by calculating more highorder terms,but the information of singularity,i.e.the information of the global behavior of the physical quantity will be lost.

In statistical mechanics,if the thermodynamic quantity of a system contains singularities,the system may have a phase transition.However,the method based on series approximations,such as the cluster expansion method,provides truncated power series approximation,i.e.approximating a thermodynamic quantity with a polynomial.The truncated series approximation,which is indeed a polynomial,cannot judge whether the thermodynamic quantity has a singularity,so it is difficult to study the phase transition by the series approximation.

In ideal quantum gases there are two characteristic lengths.One characteristic length is the thermal wavelength,which is the average de Broglie wavelength of the gas particle.The other characteristic length is the average distance between particles.When the thermal wavelength is less than the particle distance,the overlap of the wave packets of the particles is small;in this case the quantum exchange effect can be ignored and the gas is close to the classical gas.When the thermal wavelength is greater than the average distance between particles,the wave packets of the particles overlap greatly;in this case,the quantum exchange effect of identical particles is obvious,and the gas should be treated as a quantum gas.

In low temperatures and high densities,the thermal wavelength is long and the average particle distance is small,so the wave packets of particles overlaps and the quantum effect is obvious.On the contrary,in high temperatures and low densities,the wavelength is short and the average particle distance is large,so the wave packet overlap is small and the quantum effect is not obvious.In practical,it is relatively easy to obtain the high-temperature and low-density series approximation,but the high-temperature and low-density approximation is usually far away from phase transition region and one cannot directly judge whether there is a phase transition based on this.It is difficult to obtain the low-temperature and high-density property from the high-temperature and low-density approximation.In this paper,using the Padéapproximant,taking ideal Bose gases and ideal Fermi gases as examples,we consider the BEC phase transition and the low-temperature property of the Fermi system from the virial expansion which is a polynomial approximation in high temperatures and low densities.

In order to recover the information of singularity from the polynomial approximation obtained by truncating the power series,we use a rational function instead of the polynomial to approximate a function.The rational function has singularities which are the poles of the rational function.Therefore,when approximating a function by a rational function,the information of the singularity may remain.To approximate a function by a power series,we have mathematical theories like Taylor’s theorem to ensure the validity and operability of the method.For rational function approximation,however,we have no such systematic method.The idea of approximating a function by a rational function already exists in Euler’s‘Introduction to analysis of the infinite’[1].In order to approximate a function by a rational function,we still start from the power series approximation:first approximate the function by a truncated series,i.e.a polynomial,and then use a rational function to approximate the polynomial.This is the idea of the Padéapproximant.

The limitation of the truncated series approximation is that it is valid only for small perturbation parameters,for it is always a perturbation theory.Another aim of this paper is to improve a perturbation series so that the perturbation result applies also to nonperturbative regions based on the Padé approximant.

The idea to extend the range of application of a truncated series comes from the concept of analytic continuation.The domain of definition of a function f(z)may be of any shape,but the convergence region of a power-series expansion of f(z)around a point is only the largest open disc centered at the point in the domain.The convergence region of a powerseries expansion is often smaller than the definition domain of f(z)and the function f(z)is an analytic continuation of its power-series expansion.That is,the range of application of a series is extended by its sum function.Nevertheless,in practice we often only have an approximate truncated series rather than a complete series,let alone the difficulty of performing the sum of the series.Extending the range of application of a truncated series needs an approximate analytic continuation.

In order to approximately analytically continuing a truncated series,we use the Padéapproximant.The Padé approximant approximates a function by a rational function[2–4].Concretely,for an n-term truncated series,there are n expansion coefficients.We choose a rational function with n coefficients to construct a Padéapproximant.The coefficient of the Padéapproximant can be solved by equating the rational function and the truncated power series.It can be shown that the range of application of the Padéapproximant is larger than the convergence region of the corresponding power series.That is,by constructing a Padéapproximant from a truncated series,we approximately extend the range of application of the series.

The equation of state of Bose gases and Fermi gases is described by the Bose–Einstein integral and the Fermi–Dirac integral.In high temperatures and low densities,the Bose–Einstein integral and the Fermi–Dirac integral have the virial expansions which are power expansions.The Bose–Einstein integral and the Fermi–Dirac integral themselves are indeed analytic continuations of their virial expansions.However,if we only have a truncated virial expansion,i.e.we only know the first several virial coefficients,we cannot analytically continue the virial expansion by summing up the series.In the following,we show that by the Padéapproximant,we can approximately analytically continue the truncated virial expansion.

The Padéapproximant is used to cosmology[5]and the equation of state of the dark energy[6].In[7],the extended Padéapproximant is applied to nonlinear problems.The Padé approximant can be used to QCD[8,9],hadron physics[10],and nuclear physics[11].The Padéapproximant applies also to many-body systems,such as the renormalization group technique[12],the Green function of the Hubbard model,and the Haldane model[13].In[14,15],the author extracts resonance pole parameters from the phase-shift scattering data by the Padéapproximant.

In section 2,we give a brief review on how to construct a Padéapproximant from a power series.By using the Padé approximant,in section 3,we determine the BEC phase transition from the high-temperature and low-density expansion,and in section 4,we approximately analytically continue the virial expansion of the Fermi–Dirac integral.Conclusions and outlooks are given in section 5.

2.Constructing the Padéapproximant from a series:a brief review

The perturbation theory approximates an exact solution by a truncated series.The range of application of a perturbation theory is limited to a neighborhood of a certain value of a parameter.The aim of the paper is to extend the range of application of a truncated perturbation series by the Padé approximant.The treatment is indeed an approximate analytic continuation.

In perturbation theories,the approximate result is a truncated power series.The convergence region of a power series

is the largest open disc centered at zero in the domain of definition of f(z).

The Padéapproximant approximates the function f(z)by a rational function[2–4]

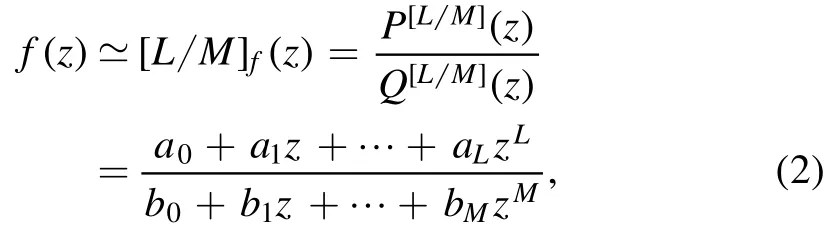
with the numerator an Lth order polynomial and the denominator an Mth order polynomial.The rational function(2)has L+M+1 coefficients to be determined,where b0can be taken to be 1.The parameters aiand biare determined by equating the rational function(2)to the power series(1):

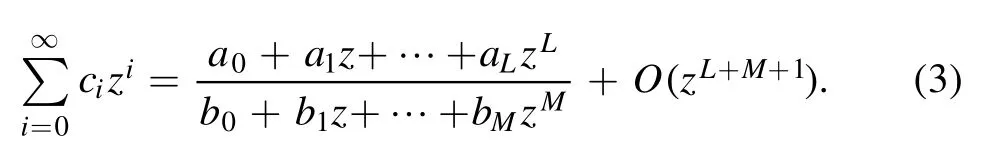
The coefficients then is given by the equation

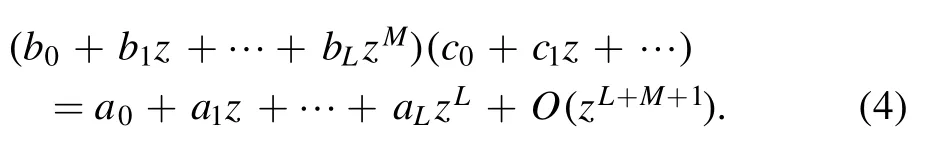
The solution reads[2–4,16]

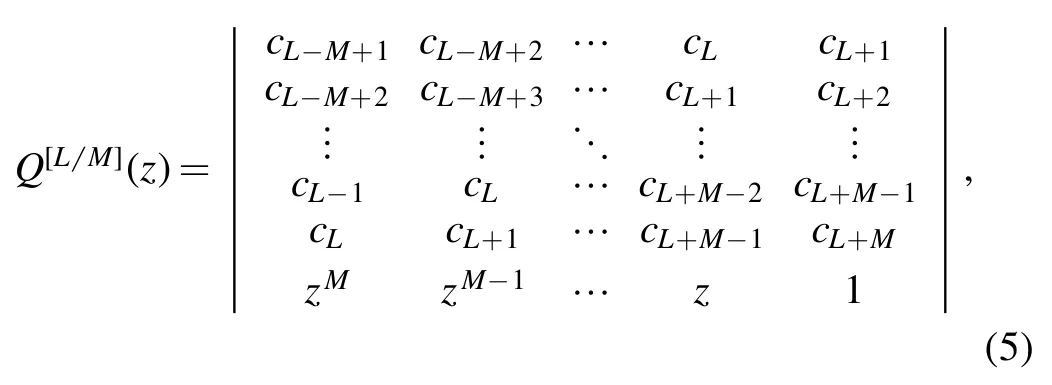
and

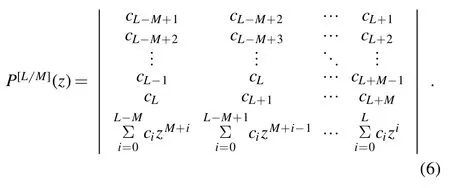
Though the coefficient in the Padéapproximant is obtained from a power series,the domain of definition of the Padéapproximant(2)is different from the convergence region of the power series(1).This allows the Padéapproximant to serve as an approximate analytic continuation of the power series.

It is worthy to note that the accuracy of a Padéapproximant(2)is often higher than that of the truncated power series from whom we construct the Padéapproximant.

3.Determining BEC phase transition from hightemperature and low-density expansion

The equation of state of ideal quantum gases is[17]

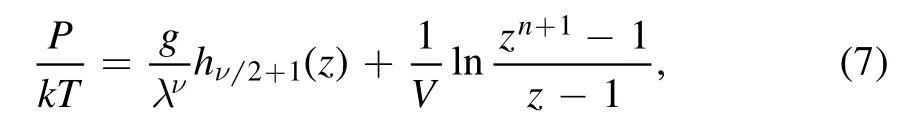
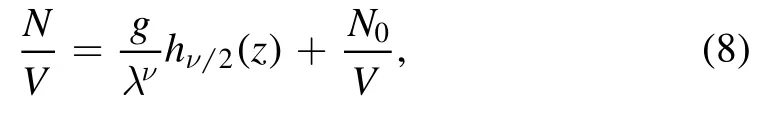
with

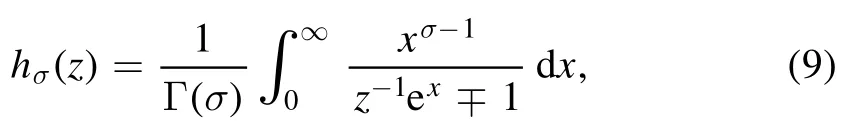
In this section,we use a truncated virial expansion which is a high-temperature and low-density expansion to determine whether there is a BEC phase transition.At first sight,it is difficult to determine the BEC phase transition from a hightemperature and low-density approximation,because BEC is a phase transition occurs only at low temperatures and high densities.In a phase transition there should exist a singularity,but the truncated virial expansion is a polynomial which has no singularity.The equation of state and the thermodynamic quantity of a three-dimensional ideal Bose gas are described by the Bose–Einstein integral.The Bose–Einstein integral

has singularities on the positive real axis of the complex fugacity plane,continuously distributing in the interval from z=1 to z→∞(see figure 1)[18,19].The high-temperature and low-density expansion of the Bose–Einstein integral,i.e.the virial expansion,is a power series.The convergence radius of the virial series is∣z∣=1.In principle,the phase transition can be determined by the convergence radius of the virial expansion,for there must be singularities on the circle of convergence.However,in practice we often only know the first few virial coefficients,i.e.only a truncated virial expansion,a polynomial,can be known.When approximating a power series by a polynomial,we lose the information of singularity.That is,if we only have a truncated virial expansion,we cannot determine whether there is a phase transition.

In order to analyze the phase transition by a truncated virial expansion,we recover the information of singularity from a truncated power series with the help of the Padé approximant.

Suppose we only know the first N terms of the virial expansion of the Bose–Einstein integral:

This approximation is valid for z≪1.To recover the information of singularity,we approximate the polynomial(11)by a rational function,i.e.the Padéapproximant:

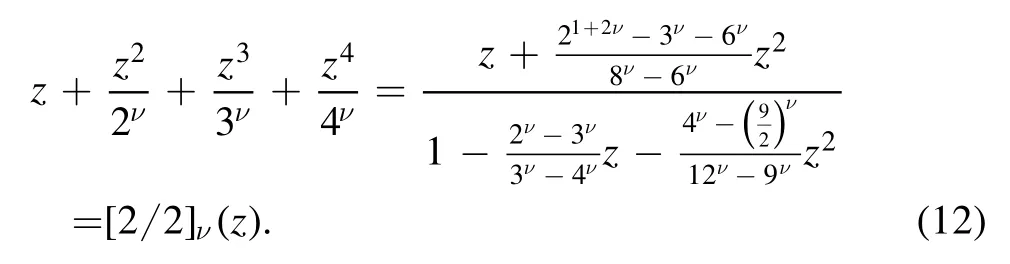
The left-hand side of equation(12)is a polynomial and has no singularity,but the right-hand side of equation(12)is a rational function with the zeroes of the denominator as its singularity.The rational function in equation(12)has two poles:

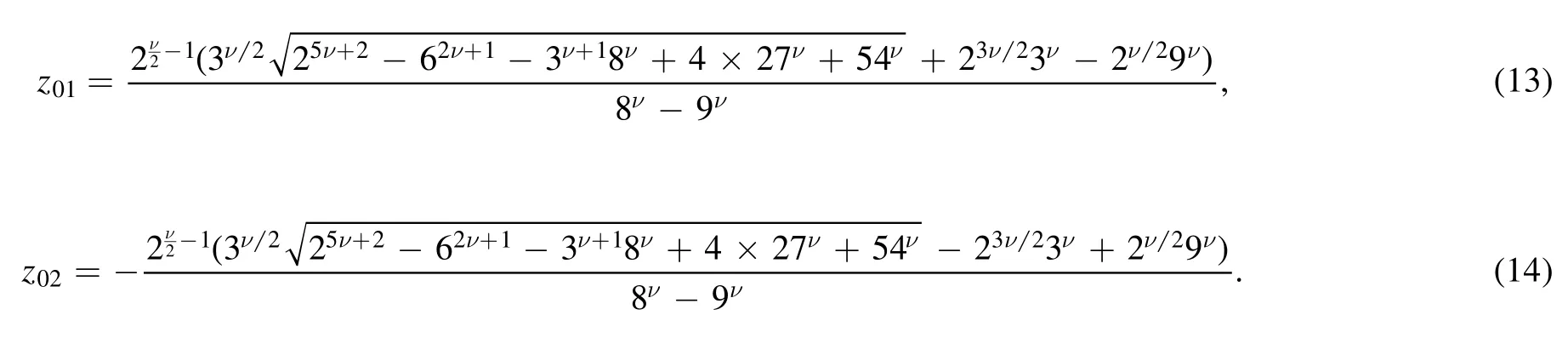
For three-dimensional Bose gases,we have

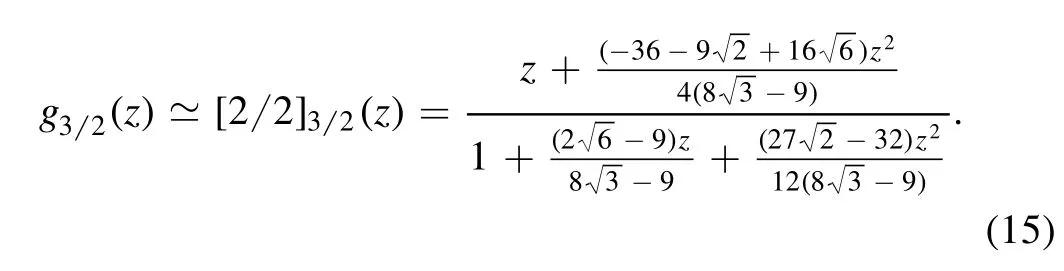
The two poles are z01=1.447 46 and z02=6.510 84.In the exact result,the singularities of the Bose–Einstein integral continuously distribute in the interval[1,∞).The existence of singularities implies that there exists a phase transition which is just the BEC phase transition.

The exact minimum value of the fugacity is z=1;the approximate minimum value given by the Padéapproximant,however,is z≃1.447 46.In order to improve the accuracy of the approximation,instead ofwe consider the Padéapproximant:

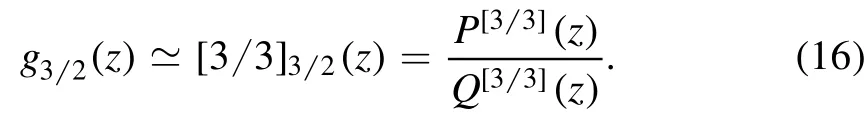
The three poles are z01=1.209 56,z02=2.329 18,and z03=11.7915;the minimum value is z≃1.209 56.

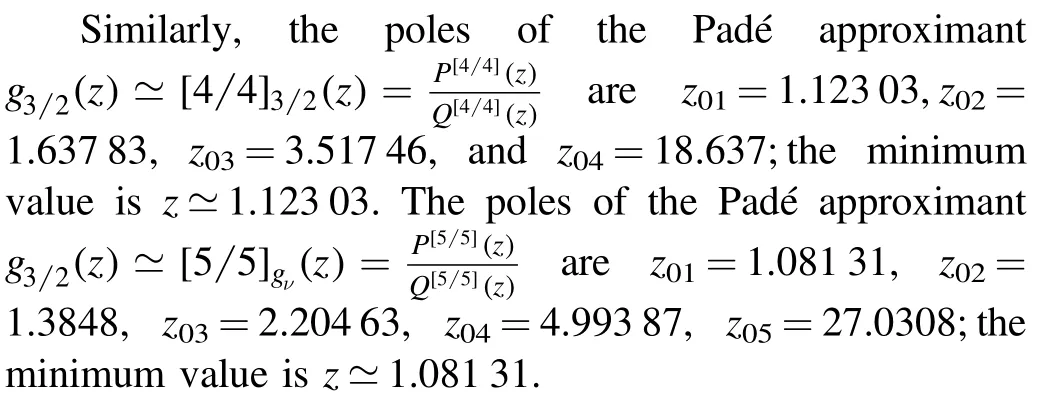
Figure 2 shows the singularities ofg32(z)and its Padé approximants[2 2]32(z)and[3 3]32(z).It can be seen that as the accuracy increases,the minimum value of the fugacity is getting closer and closer to the accurate result 1.

Figure 1.The convergence region of the virial expansion is the largest open disc centered at zero in the domain of definition of the Bose–Einstein integral gν(z).

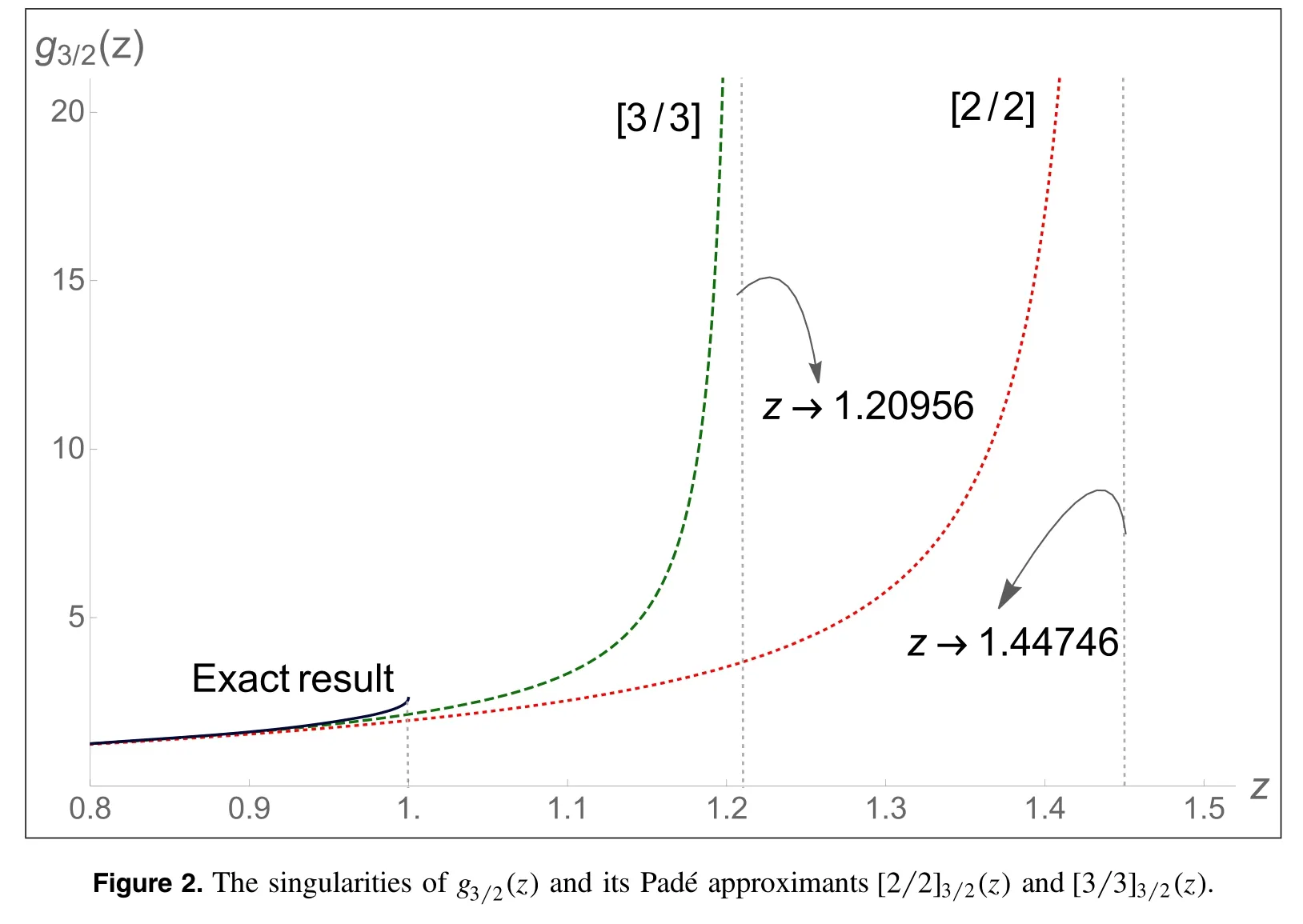
Figure 3.The convergence region of the virial expansion is the largest open disc centered at zero in the domain of definition of the Fermi–Dirac integral fν(z).

In a word,with the help of the Padéapproximant,we can determine the BEC phase transition which occurs only at low temperatures and high densities from the first several terms of a high-temperature and low-density expansion.

4.Approximately analytically continuing high temperatures and low densities to low temperatures and high densities:Fermi–Dirac gases

4.1.The Fermi-Dirac integral and the virial expansion

The Fermi–Dirac integral is

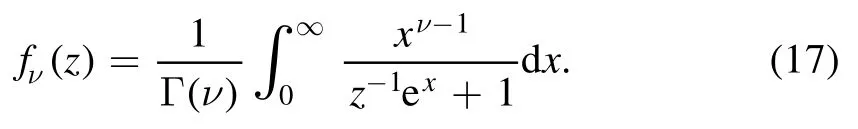
The virial expansion,a high-temperature and low-density expansion,of the Fermi–Dirac integral is a power series around the fugacity z=0[22,23],

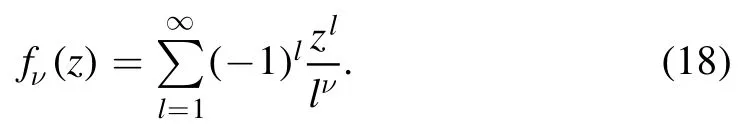
The Fermi–Dirac integral in the complex z-plane has a singularity line from z=-1 to-∞.The Fermi–Dirac integralfν(z )is analytic in the complex z-plane with the exception of the interval(-∞,-1) on the negative real axis[18,19].The convergence region of the virial expansion(18),due to Abel’s theorem,is an open disc of radius∣z∣=1 centered at zero,since the point z=-1 is a singularity of the Fermi–Dirac integral in the complex z-plane,see figure 3.Therefore,the virial expansion is only valid for z＜1,i.e.the high-temperature and low-density case.For low temperatures and high densities,in which the fugacity z>1,however,the virial expansion is invalid.

Though the virial expansion(18)is valid only for z＜1,the Fermi–Dirac integral is real analytic on the whole positive real axis,i.e.the range of the value of the fugacity is 0＜z＜∞.This allows us to seek a low-temperature and high-density approximation by analytically continuing the virial expansion.

4.2.Approximate analytical continuation:the Padé approximant

The virial expansion is a high-temperature and low-density expansion,which is valid only for z＜1.We now extend the viral expansion to low temperatures and high densities,the case of z>1,by the Padéapproximant.

First consider the case that the first 4 virial coefficients of the Fermi–Dirac integral are known,

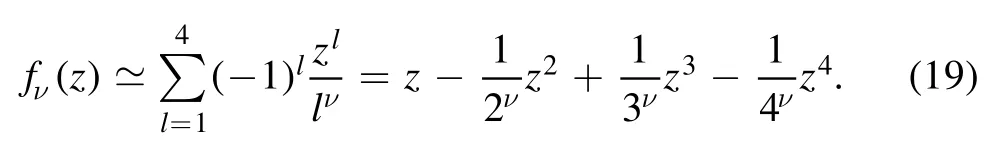
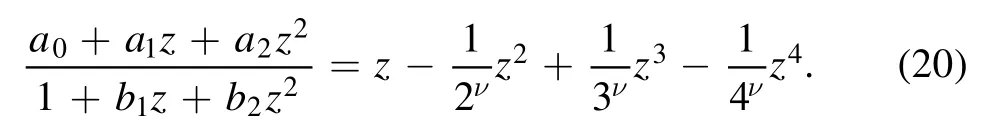
By Eqs.(5)and(6)we have

with

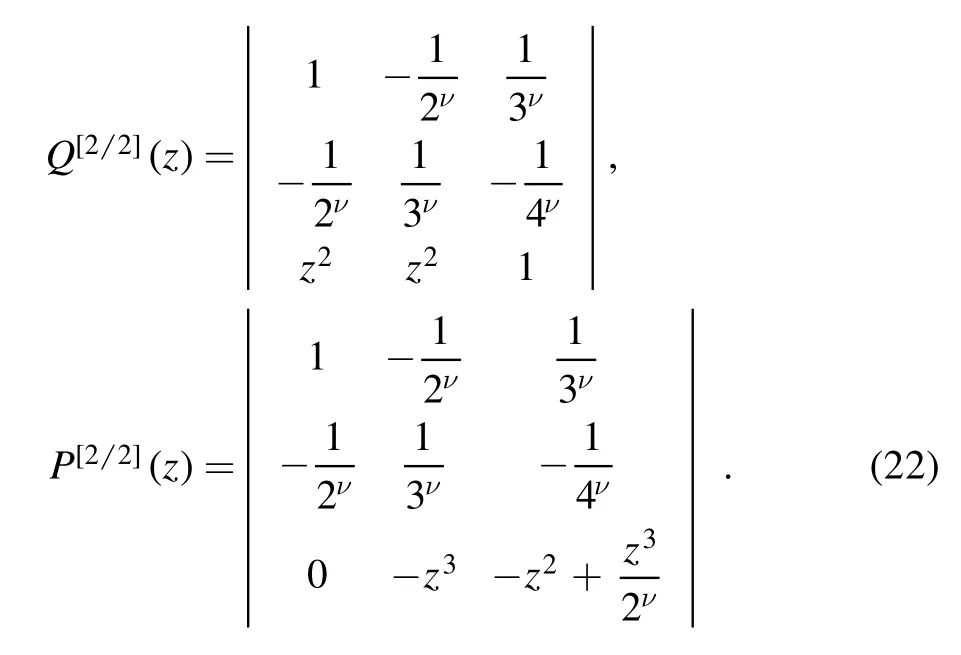
Next consider the case that the first 6 virial coefficients of the Fermi–Dirac integral are known,

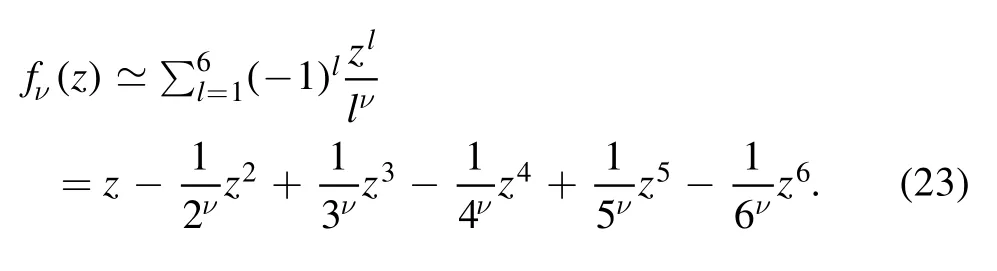
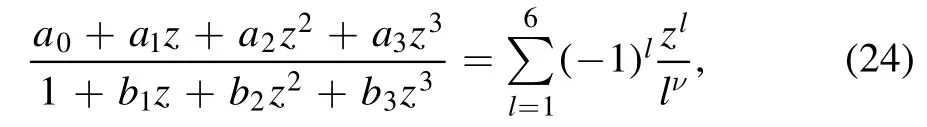
by Eqs.(5)and(6),gives

where

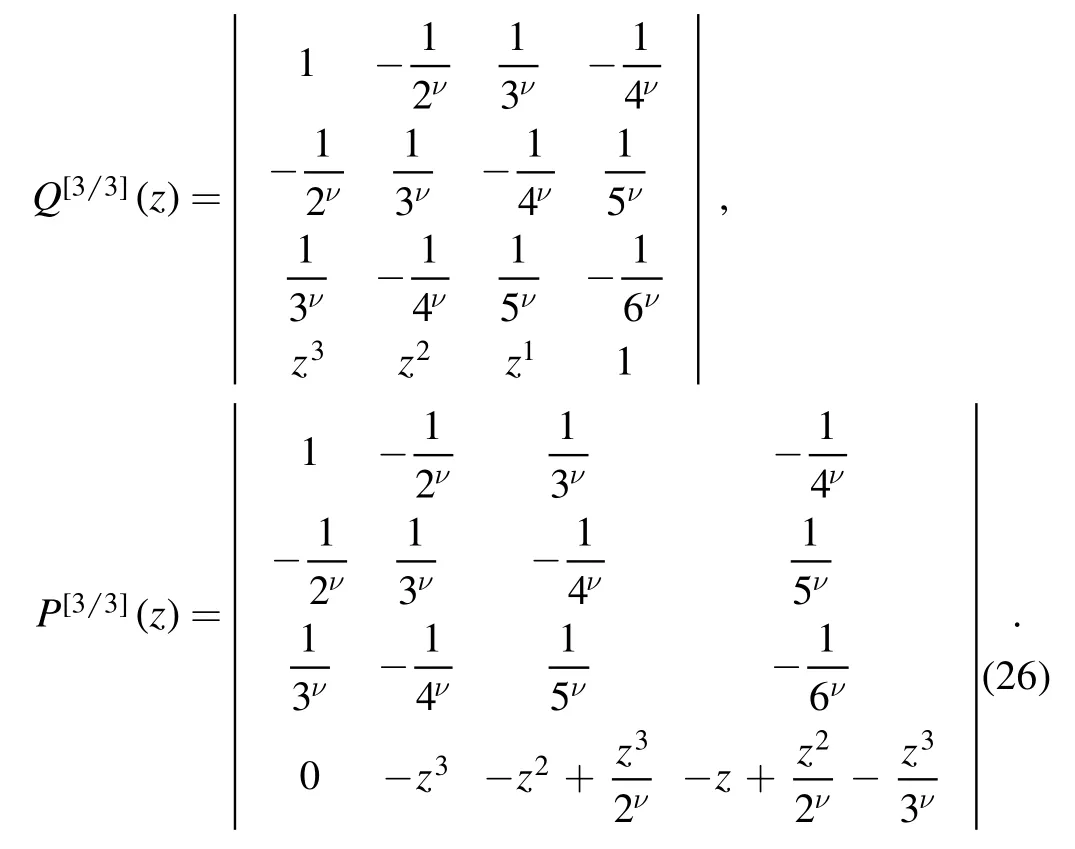
Though the coefficients of the Padéapproximant(25)are all calculated from the virial coefficient,the range of application of the Padéapproximant is larger than the region of convergence of the virial expansion.The virial expansion is a power-series expansion,whose region of convergence is a disc∣z∣＜1,i.e.the virial expansion diverges for∣z∣≥1.Nevertheless,the Padéapproximant(25)is valid even if∣z∣≥1.To show this,we compare the exact Fermi–Dirac integral,the Padéapproximant,and the virial expansion in figure 4.We can see that even for z>1,the Padéapproximant is very close to the exact result,while the virial expansion is invalid when z>1.

4.3.Various choices of the Padéapproximant

The Padéapproximant is an approximation and the choice of constructing the Padéapproximant is not unique.In the above,we consider two constructions of the Padéapproximant,andHere we compare various constructions of the Padéapproximant.

For z>1,the virial expansion fails no matter how many terms of the power series are taken into account,for the convergence region of the virial expansion is a disc of radius∣z∣=1.However,the Padéapproximant,though constructed from a truncated virial expansion,is valid for z>1.

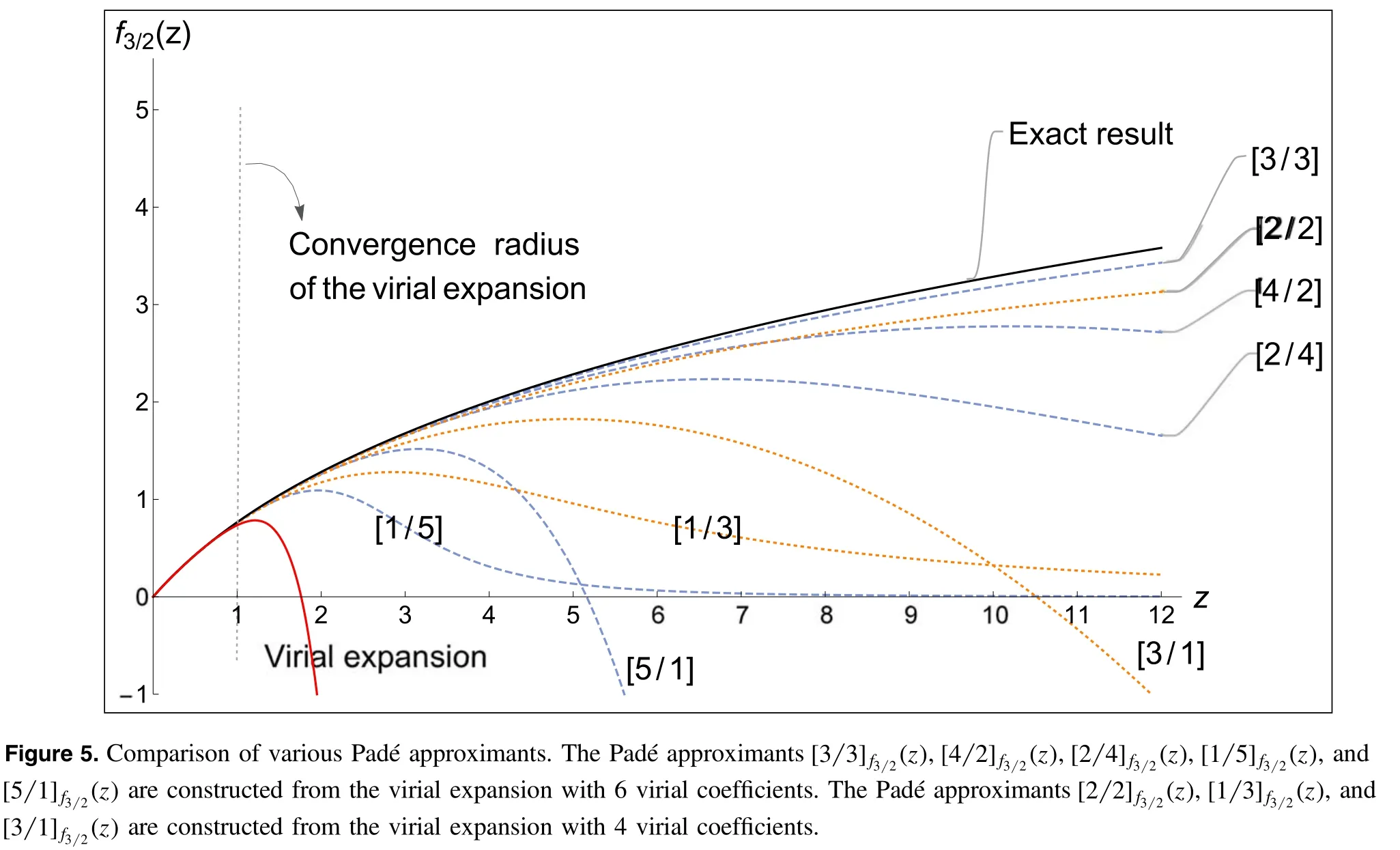
From the virial expansion of 4 virial coefficients,we can construct three Padéapproximants:andFrom the virial expansion of 6 virial coefficients,we can construct five Padéapproximants:andThe comparison of these Padéapproximants are shown in figure 5.It can be seen that the Padéapproximant of the formi.e.the orders of the polynomials in the numerator and in the denominator are the same,is the better one.

5.Conclusions and outlooks

In the present paper,we suggest a method that allows us to infer the low-temperature and high-density result which is obtained by calculation or observation from the high-temperature and low-density result of high temperature.

The virial expansion for quantum gases is a high-temperature and low-density approximation.Starting from a a truncated virial series,we infer the BEC phase transition for a Bose gas and infer the low-temperature and high-density properties for a Fermi gas by the Padéapproximant.

An exact series solution has a natural analytic continuation:the sum function which is obtained by summing up the series[24].Nevertheless in perturbation theory,we often only have an approximate truncated series.The truncated series is an approximation.To extend the range of application of a truncated series needs an approximate analytic continuation.In this paper,we use the Padéapproximant to implement the analytic continuation.Furthermore,we can also perform approximate calculations in a small parameter range first,and then use Padéapproximant to seek results in a larger parameter range.For example,there are some methods developed for few-body systems,but when the number of particles are large,the calculation amount will increase dramatically[25–27].The Padéapproximationant may help us deal with systems with fewer particles first,and then approximately analytically continue to systems with more particles.

The method considered in the present paper in principle applies to any perturbation theory so long as the approximation is represented by a truncated series.Most results of perturbation theories in physics are given by a truncated series,such as the Feynman diagram in quantum field theory,the cluster expansion in statistical mechanics,the perturbation method in classical and quantum mechanics.In these problems,we can use the method discussed in the present paper to extend the perturbation result to nonperturbative region.

Acknowledgments

We are very indebted to Dr G Zeitrauman for his encouragement.This work is supported in part by The Fundamental Research Funds for the Central Universities under Grant No.2020JKF306,Special Funds for theoretical physics Research Program of the NSFC under Grant No.11 947 124,and NSFC under Grant Nos.11 575 125 and 11 675 119.