Chiral effective Lagrangian for excited heavy-light mesons from QCD
Qing-Sen Chen,Hui-Feng Fu,*,Yong-Liang Maand Qing Wang
1 Center for Theoretical Physics,College of Physics,Jilin University,Changchun 130012,China
2 School of Fundamental Physics and Mathematical Sciences,Hangzhou Institute for Advanced Study,UCAS,Hangzhou,310024,China
3 International Center for Theoretical Physics Asia-Pacific(ICTP-AP)(Beijing/Hangzhou),UCAS,Beijing 100190,China
4 Department of Physics,Tsinghua University,Beijing 100084,China
5 Center for High Energy Physics,Tsinghua University,Beijing 100084,China
Abstract We derive the chiral effective Lagrangian for excited heavy-light mesons from QCD under proper approximations.We focus on the chiral partners with and which amounts to(1+,2+)and(1-,2-)states respectively.The low energy constants including the masses of the chiral partners are calculated.The calculated spectrum for the excited mesons are found roughly consistent with experimental data.In addition,our results indicate that quantum numbers of BJ(5970)can be identified with 1-or 2-.
Keywords:chiral effective Lagrangian,heavy-light meson,QCD,chiral partner
1.Introduction

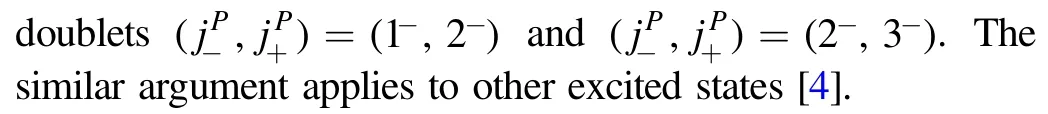
For the light quarks,the chiral symmetry,which is dynamically(and explicitly)broken,is essential.If the chiral symmetry were preserved,the heavy-light mesons with the same jlbut opposite parities would be degenerated.We call them chiral partners.The mass splitting between the chiral partners reflects the chiral symmetry breaking[5,6].
Since heavy-light mesons capture the features of both heavy quark symmetry and chiral symmetry,it is ideal to study heavy-light meson phenomena using the chiral Lagrangian incorporating heavy quark symmetry.Since 2000,a series of researches on deriving the chiral effective Lagrangian from QCD have been carried out in[7–15].The advantage of this method is that it can establish the analytic relationships between the low energy constants(LECs)of the chiral effective theory and QCD.Recently,we used the same methodology to derive the chiral Lagrangian incorporating heavy quark symmetry from QCD to study heavy-light mesons[16,17].In these works,we focused on the chiral partnersandThe low energy constants of the effective Lagrangian are expressed in terms of the light quark self-energy which can be calculated by using Dyson–Schwinger equations or lattice QCD.Numerical results of the low energy constants are globally in agreements with the experiment data.

The remaining part of this paper is organized as follows.In section 2,for convenience,we give the general form of the chiral Lagrangian of the excited heavy-light mesons.In section 3 we derive the excited heavy-light meson Lagrangian from QCD and determine the expression of low energy constants.The numerical results calculated by using the quark self-energy obtained from a typical Dyson–Schwinger equation and from lattice QCD are given in section 4.Section 5 is devoted to discussions.The expressions of the LECs with the contribution from the renormalization factor of quark wave function are given in appendix.
2.Chiral effective Lagrangian for excited heavy-light mesons




where


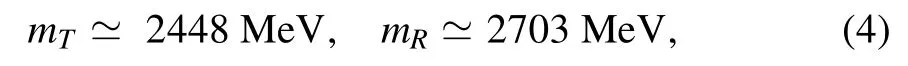
which yields the mass splitting

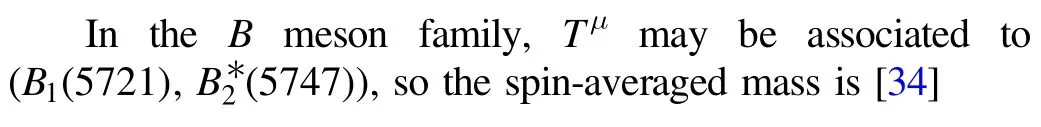

For the(1-,2-)doublet,the situation is subtle since the quantum numbers of the possible candidates in PDG are not well determined.With respect to the mass splitting between chiral partners in the charmed meson sector,the masses of the states in the Rμdoublet should have masses~6000 MeV.This means that it is reasonable to identify the quantum numbers of the state BJ(5970)as 1-or 2-or maybe the 1-and 2-states have nearly degenerate masses.
3.Chiral effective Lagrangian of excited heavy-light mesons from QCD
In this section,we follow our previous work[16]to derive the chiral effective Lagrangian for excited heavy-light mesons withand its low energy constants.
The generating functional of QCD with an external source J(x)is

where q(x),Q(x)and Gμ(x)are the light-quark,heavy-quark and gluon fields,respectively.
By integrating in the chiral field U(x)and the heavy-light meson fields,and integrating out gluon fields and quark fields,we obtain the effective action for the chiral effective theory as[16]

where Π2andare the heavy-light meson field and its conjugate,respectively and,mQis the mass of heavy quark Q.is the self-energy of the light quark propagator.I1=diag(1,1,0)and I4=diag(0,0,1)are matrices in the flavor space.JΩis the chiral rotated external source.
Before going further,we would like to make a few comments on the approximations made during the derivation of equation(8).The details are given in the appendix A of[16].
•When integrating in the heavy-light meson fields,we have taken the heavy quark limit which brings in an uncertainty of order 1/mQ.And,to integrate out the gluon and quark fields,we left infinitely many gluon Green functions in the action.
•Further approximations,i.e.the chiral limit,the large Nclimit and the leading order in dynamical perturbation,are made in order for the derived action could serve practical purposes.The chiral limit causes an uncertainty of order mu,d,and large Nclimit suffers from 1/Nccorrections.Taking the leading order in dynamical perturbation is a similar technique as the rainbow-ladder approximation in the Dyson–Schwinger–Bethe–Salpeter(DSBS)formulism.The errors brought in by this last approximation is hard to be estimated quantitatively,but its justification is supported by the relatively success of the rainbow-ladder approximation in the DSBS formulism.
Since the introduced heavy-light meson field Π2is a bilocal field,we need a suitable localization on Π2fields to get a local effective Lagrangian.Here we follow the approach in[32],and take the following localization conditions

where


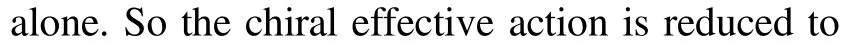

In order to obtain the chiral effective Lagrangian,we need expand the actionwith respect to the fields U,andThe kinetic terms of the excited heavylight meson fields Tμ(a similar equation holds for Rμ)arise from

Taking the derivative expansion up to the first order,we obtain
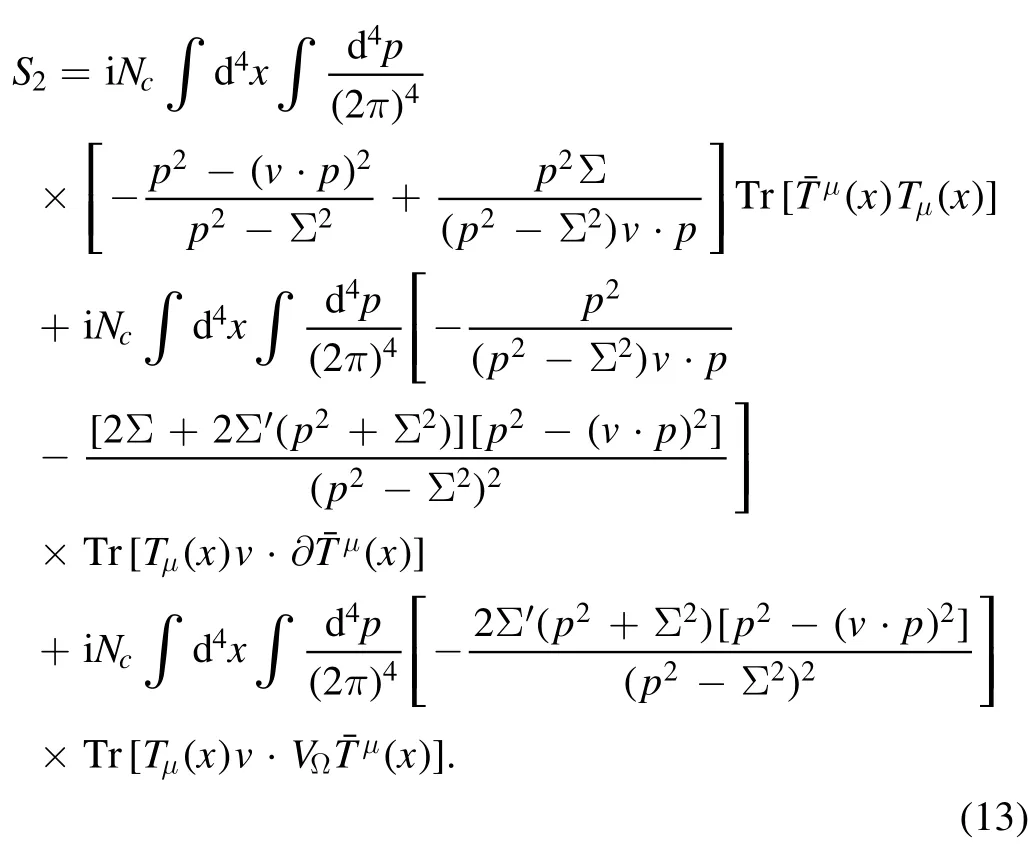
In the calculation,we have used the relationIt is easy to identify the mass term and the kinetic term in equation(13).In addition,an interaction term between the Tμfields and VΩfields also appear in equation(13)because we have takenin the calculation to retain the correct chiral transformation properties in the theory[8].
The interaction between the heavy-light meson field Tμand the light Goldstone boson field S3can also be obtained by expanding the actionwith respect to the external JΩ,andas

Upto the first order of the derivative expansion,one obtains

Summing up equations(13)and(15),we obtain the expressions of the constants mTand gTas

with ZTbeing the wave function renormalization factor

Following the same procedure,one can get the LECs associated to Rμ.The only difference in the calculation is the relationwhich induces the differences between the LECs of Rμand those of Tμ.The LECs associated to Tμread

We also obtain the coupling constant between the chiral partner fields Tμand Rμas

In the above expressions,Σ(-p2)stands for self-energy of light quarks to be calculated from QCD.This is an apparent indicator that we have established a connection between the low energy constants of the chiral effective theory and the Green functions of QCD.
4.Numerical results and discussions
In order to obtained the explicit numerical values of the LECs,we first need to obtain the light quark self-energy Σ(-p2).As in our previous works[16,17],we use two method to determine Σ(-p2)for comparison,namely,the gap equation,i.e.the Dyson–Schwinger equation for quarks,and the fittings from lattice QCD.
For the Dyson–Schwinger equation method,we use the differential form of the gap equation[8]:

where the boundary conditions are

with αsbeing the running coupling constant of QCD.Λ′is an ultraviolet cutoff regularizing the integral,which is taken Λ′→∞eventually.To solve the equation(19),we take a model description for αsgiven in[35]

For convenience,we call it Gribov-Zwanziger(G-Z)Model.The parameters are M2=4.303 GeV2,(M2+m2)=0.526 GeV2and λ4=0.4929 GeV4[35].α0is a model parameter to be determined.Although the UV behavior of G-Z formalism is inconsistent with QCD,it should not have a sizable impact on our results because the LECs are mostly controlled by its low energy behavior.
Solving the gap equation,we obtain Σ(-p2).Then the LECs are calculated according to equations(16)–(18).It is clear that the integrals of the LECs have a physical ultraviolet cutoff Λcwhich should be of the order of the chiral symmetry breaking scale and serves as another parameter in our calculations.Since we are studying excited states,the cutoff Λcshould take a bit larger value than 1 GeV.For the excited states we are considering now,the energy of the light quark in the chromoelectrical fields generated by the heavy quark could be up to~1.45 GeV,so Λctaking a value1.5 GeV would be more appropriate for the present situation.For the G-Z model,we take Λc=1.6 GeV and determine the model parameter a0by requiring the calculated fπbe consistent with the corresponding experimental value.We find that using a0=0.52 we can obtain the well-established quantity fπ.The results are listed in table 1.For comparison,we also list the numerical results obtained with different a0's in the table.To give an intuitive impression,we draw the running coupling constant αscalculated with the G-Z formalism at a0=0.52 in figure 1.The light quark self-energy Σ(-p2)solved by the gap equation(19)is shown in figure 2.

Table 1.The heavy-light meson masses and the coupling constants calculated from the G-Z Model with Λc=1.6 GeV.The empirical values are give for comparison.
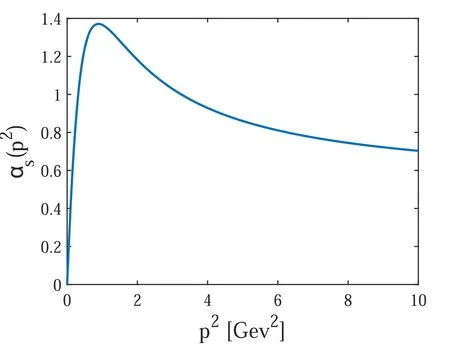
Figure 1.Running coupling constant of the G-Z model with a0=0.52.

Figure 2.The lattice fittings of M(-p2)and Z(-p2)given in[36]and Σ(-p2)from the gap equation with G-Z Model.
Since there are more and more excited states observed experimentally whose masses and quantum numbers have not been confirmed yet,we focus on the masses of the chiral partners in our method in this work and hopefully could help identifying some excited mesons.The mass splittingΔm is a direct indicator of the chiral symmetry breaking.In our calculations,it is completely originated from the non-vanishing of the quark running mass,which can be reflected by the quark condensate or the value of Σ(0).From table 1,one can see thatΔm increases as the quark condensate or Σ(0)increases.At a0=0.52,we findΔm=379 MeV which is a bit larger than the expected value~255 MeV as given in(4).This is not surprising because on one hand the measured masses of the relevant excited mesons are not accurate,and on the other hand our results are suffering from uncertainties due to theignorance of the 1/mQcontributions,1/Nccontributions,etc,as indicated in the previous section.Since mu,dboth are a few MeVs which are much smaller than the chiral scale,so we do not expect large errors from taking the chiral limit.For the 1/Nccontributions,one may expect relative errors of roughly~30%(which is of course a too naive estimation and more precise values can only be obtained by calculating the 1/Nccorrections for LECs).For the 1/mQcontributions,the results for the ground states given in[17]may give a quantitative intuition.It is shown in[17]that 1/mQcorrections toΔm ofheavy-light mesons are about~100MeV for mcand about tens MeVs for mb.



Now,let us turn to the results using the quark self-energy fitted from lattice QCD.We use the lattice fittings for the quark wave function renormalization Z(-p2)and the running quark mass M(-p2)given in[36].The formula of LECs shown in equations(16)–(18)can be directly extended to incorporate the contributions from Z(-p2).The relevant expressions are given in appendix.The functions Z(-p2)and M(-p2)are also plotted in figure 2.The numerical results of LECs calculated by using these lattice fittings are given in table 2.There is no free parameters in the functions of M(-p2)and Z(-p2).Typically,the running quark mass and the wave function renormalization are calculated in the negative p2region.Extrapolation of these functions into the complex p2-plane is known to be technically difficult.Fortunately,the quantities we are calculating now only involve M(-p2),Z(-p2)and Σ(-p2)in the negative p2region.Because,the existence of the cutoff Λcguarantees that the integrations in equations(16)–(18)and those in the appendix should only be performed within the range≤Λc.This would be easier understood by translating the momentum p into the Euclidean momentum via Wick rotation.
From table 2,one can see that the numerical results of LECs are comparable to the results from the G-Z model when Λc=1.6 GeV,which implies that Z(-p2)does not have significant impacts on the excited states.The physical masses areandGeV for excited D mesons,andandfor excited B mesons.The conclusions could be drawn from these results are the same as we have in the G-Z model.

Table 2.LECs calculated from lattice fittings given in[36].The empirical values are give for comparison.



where miis the mass of the decaying meson;mfand Efare the mass and the energy of the heavy-light meson in the final states respectively;Eπand pπare the energy and the magnitude of the momentum of the pion,respectively.
Given the assignments of the D mesons,we find

where(G-Z)denotes results from the G-Z model with a0=0.52;(Lat.)denotes results from the lattice-fittings with Λc=1.6 GeV.For the B mesons,the assignments of R doublet is yet unclear.If BJ(5970)is the 1-state in the R doublet,then we have

If BJ(5970)is the 2-state in the R doublet,then we have

In the future,when the corresponding experimental results are available,our theoretical predictions could help testing the assignments of these excited mesons.
5.Conclusions

As more and more excited states of charmed mesons and bottom mesons are discovered in experiments,it will be an interesting and important research to extend our method to obtain the chiral effective Lagrangian of heavy-light mesons with arbitrary spins.Since this extension is straightforward,we will not go to details here.
We finally want to say that,so far,we did not discuss the chiral partner structure of the heavy-light mesons including a strange quark.One of the reasons is that the quark content of some of these mesons is still under debate.For example,the mesons Ds0(2317)and Ds1(2460)which can be arranged to the G doublet with quantum numbers G=(0+,1+)are regarded as the chiral partners of D and D*,respectively,in the H doublet with quantum numbers H=(0-,1-)[37].The molecular state interpretation of these mesons and their bottom cousins cannot be ruled out[38–40].We leave the discussion of these strange mesons as future works.
Acknowledgments
The work of YLM was supported in part by National Science Foundation of China(NSFC)under Grant No.11 875 147 and No.11475071.H-F Fu was supported by NSFC under Grant No.12047569.QW was supported by the National Science Foundation of China(NSFC)under Grant No.11 475 092.
Appendix.Formula for lecs with Z(−p2)
The quark propagator can be generally written as

where Z(-p2)=1/A(-p2)stands for the quark wave function renormalization and M(-p2)=B(-p2)/A(-p2)is the renormalization group invariant running quark mass.After a series of calculations,we can get the LECs with Z(-p2)as follows:

ORCID iDs
 Communications in Theoretical Physics2021年6期
Communications in Theoretical Physics2021年6期
- Communications in Theoretical Physics的其它文章
- Intermediate symmetric construction oftransformation between anyon and Gentile statistics
- Proton radioactivity within the generalized liquid drop model with various versions of proximity potentials
- Joule–Thomson expansion of higher dimensional nonlinearly AdS black hole with power Maxwell invariant source
- Notch fatigue of Cu50Zr50 metallic glasses under cyclic loading:molecular dynamics simulations
- Eigen microstates and their evolutions in complex systems
- Non-similar mixed convection analysis for magnetic flow of second-grade nanofluid over a vertically stretching sheet
