Analysis of the tetraquark and hexaquark molecular states with the QCD sum rules
Zhi-Gang Wang
Department of Physics,North China Electric Power University,Baoding 071003,China
Abstract In this article,we construct the color-singlet-color-singlet type currents and the color-singlet-colorsinglet-color-singlet type currents to study the scalar D *D D**tetraquark molecular states and the vector D*D*D*DD**hexaquark molecular states with the QCD sum rules in details.In calculations,we choose the pertinent energy scales of the QCD spectral densities with the energy scale formulaand for the tetraquark and hexaquark molecular states respectively in a consistent way.We obtain stable QCD sum rules for the scalartetraquark molecular states and the vector D*DD*¯*hexaquark molecular state,but cannot obtain stable QCD sum rules for the vector D*DD**hexaquark molecular state.The connected(nonfactorizable)Feynman diagrams at the tree level(or the lowest order)and their induced diagrams via substituting the quark lines make positive contributions for the scalar D D**tetraquark molecular state,but make negative or destructive contributions for the vector D*DD**hexaquark molecular state.It is of no use or meaningless to distinguish the factorizable and nonfactorizable properties of the Feynman diagrams in the color space in the operator product expansion so as to interpret them in terms of the hadronic observables,we can only obtain information about the short-distance and long-distance contributions.
Keywords:tetraquark molecular states,hexaquark molecular states,QCD sum rules
1.Introduction
The QCD sum rules approach,which was developed about forty years ago by Shifman,Vainshtein and Zakharov,has become a widely used theoretical tool in studying the hadron properties,such as the masses,decay constants,form-factors,coupling constants,light-cone distribution amplitudes,etc[1–3].We carry out the operator product expansion for the correlation functionsΠ(p2)in the deep Euclidean space,which represent the short-distance quark–antiquark fluctuations and can be treated in perturbative QCD.A certain energy scale μ is necessary to separate the regions of the short distance and long distance,the short-distance quark-gluon interactions at the momenta greater thanμ2are included in the Wilson’s coefficients,while the long-distance quark-gluon interactions or soft quark-gluon effects at the momenta less thanμ2are absorbed into the vacuum condensates,which have universal values and are applicable in all the QCD sum rules.On the other hand,at the positive p2,the correlation functionsΠ(p2)can be expressed in terms of hadronic observables.The correlation functionsΠ(p2)obtained at an arbitrary pointp2<0 relate to the hadron representation through dispersion relation.
Experimentally,a number of charmonium-like and bottomonium-like states,in other words the exotic X,Y and Z states,were observed after the observation of the X(3872)by the Belle collaboration[4].In 2006,R D Matheus et al assigned the X(3872)to be the diquark–antidiquark type tetraquark state with the spin-parity-charge-conjugationJPC=1++,and studied its mass with the QCD sum rules[5].Thereafter the QCD sum rules become a powerful theoretical approach in studying the exotic X,Y,Z and Pcstates and have given many successful descriptions of the hadron properties,such as the masses and decay widths[6].As the exotic X,Y,Z and Pcstates lie near the meson–meson or meson-baryon thresholds,we can assign them to be the tetraquark or pentaquark molecular states naively and intuitively,and interpolate them with the color-singlet-colorsinglet type currents[7–10].
The color-singlet-color-singlet type currents,which consist of four valance quarks,couple potentially to the tetraquark molecular states,however,the quantum field theory does not forbid the non-vanishing couplings between the color-singlet-color-singlet type currents and meson–meson scattering states.For the color-singlet-color-singlet type currents,Lucha,Melikhov and Sazdjian assert that the Feynman diagrams can be divided into factorizable and nonfactorizable diagrams in the color space,the contributions at the orderwithk≤1,which are factorizable in the color space,are exactly canceled out by the meson–meson scattering states at the hadron side,the nonfactorizable diagrams,if having a Landau singularity,begin to make contributions to the tetraquark molecular states,the tetraquark molecular states begin to receive contributions at the order[11,12].The assertion is also applicable for the diquark–antidiquark type currents,as they can be rearranged into the color-singletcolor-singlet type currents through the Fierz re-ordering.
In[13],we provide solid proofs to show that the Landau equation is of no use to study the Feynman diagrams in the QCD sum rules for the tetraquark molecular states and tetraquark states,such as the quarks and gluons are confined objects and thus cannot be put on mass-shell;the operator product expansion is carried out at the regionrather than at the regionp2>Δ2to have Landau singularities;the lowest order Feynman diagrams have Landau singularities at the regionp2>Δ2,if not assuming the factorizable diagrams in the color space only make contributions to the two-meson scattering states,where theΔ2denotes the thresholds.We refute the assertion of Lucha,Melikhov and Sazdjian in details,and use two color-singlet-color-singlet type currents as examples to show that the meson–meson scattering states alone cannot saturate the QCD sum rules,while the tetraquark molecular states alone can saturate the QCD sum rules,the tetraquark molecular states begin to receive contributions at the orderrather than at the order[13].In the light flavor sector,Lee and Kochelev study the two-pion contributions in the QCD sum rules for the scalar mesonf0(600)as the tetraquark state,and observe that the contributions at the orderwithk≤1 in the operator product expansion cannot be canceled out by the two-pion scattering states[14].
In this article,we extend our previous work to study theandtetraquark and hexaquark molecular states with the QCD sum rules,and examine whether or not it is necessary to distinguish the factorizable and nonfactorizable properties of the Feynman diagrams in the color space so as to interpret them in terms of the hadronic observables.Phenomenologically,theandhexaquark molecular states have been studied with the heavy quark spin symmetry[15,16],theandhexaquark molecular states have been studied with the fixed center approximation to the Faddeev equations[17,18].In[19],we study thehexaquark molecular state with the QCD sum rules by considering the contributions of the vacuum condensates up to dimension-16.In the early works[20–22],themolecular states were studied via the QCD sum rules by carrying out the operator product expansion up to the vacuum condensates of dimension-6,the Borel platforms were not very flat.In[23],the*molecular states are studied via the QCD sum rules by carrying out the operator product expansion up to the vacuum condensates of dimension-8 and partly taking into account the perturbative corrections to the perturbative terms,however,too large continuum threshold parameters and too large energy scales of the QCD spectral densities are taken.In this article,we study the molecular states of the D*-mesons in a consistent way.
The article is arranged as follows:we derive the QCD sum rules for the masses and pole residues of the**,D*D*andD*DD**tetraquark and hexaquark molecular states,and examine the properties of the Feynman diagrams in section 2;in section 3,we present the numerical results and discussions;and section 4 is reserved for our conclusion.
2.QCD sum rules for the tetraquark and hexaquark molecular states
Firstly,let us write down the two-point correlation functions Π(p)andΠμν(p)in the QCD sum rules,
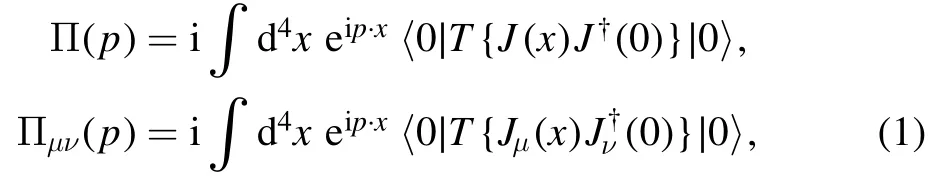
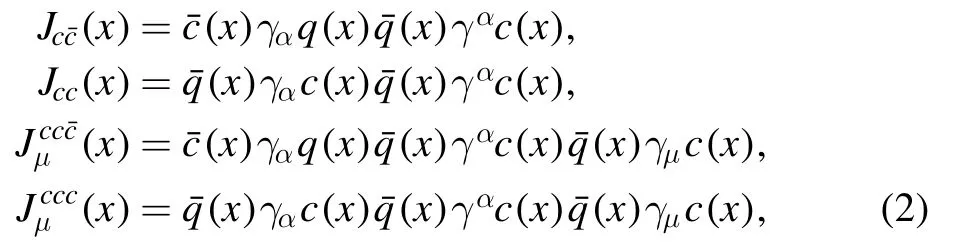

At the hadron side of the correlation functionsΠ(p)and Πμν(p),we isolate the contributions of the lowest hidden-charm and doubly-charmed tetraquark molecular states and the charmed plus hidden-charm and triply-charmed hexaquark molecular states to obtain the hadron representation

where the subscripts T and H denote the scalartetraquark molecular states and the vectorhexaquark molecular states,respectively,and we have used the definitions for the pole residues,
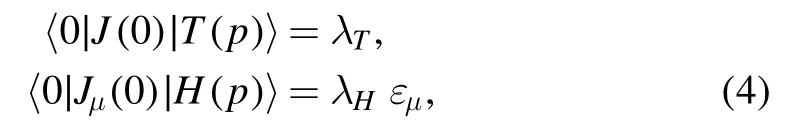
theεμare the polarization vectors of the vector hexaquark molecular states.In[13],we observe that,for the colorsinglet-color-singlet type currents,the meson–meson scattering states alone cannot saturate the QCD sum rules,while the tetraquark molecular states alone can saturate the QCD sum rules,the net effects of the two-meson scattering states amount to modifying the pole residues considerably without influencing the predicted masses.In this article,we only take into account the tetraquark and hexaquark molecular states,as the widths of those molecular states,which absorb the contributions of the two-meson or three-meson scattering states,are unknown.
At the QCD side of the correlation functionsΠ(p)and Πμν(p),we contract the q and c quark fields with the Wick’s theorem,and obtain the results,
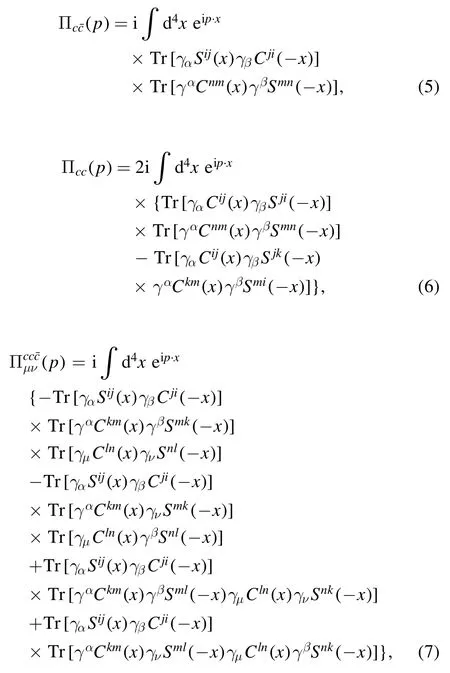

where the Sij(x)and Cij(x)are the full light and heavy quark propagators,respectively,

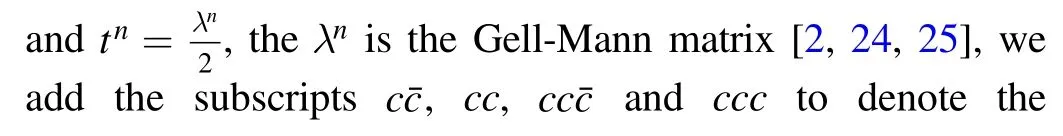

In equations(5)–(8),we assume dominance of the vacuum intermediate state tacitly,and insert the vacuum intermediate state in all the channels and neglect the contributions of all the other states.In the original works,Shifman,Vainshtein and Zakharov took the factorization hypothesis according to two reasons[1].One is the rather large value of the quark condensate〈,the other is the duality between the quark and physical states,which implies that counting both the quark and physical states may well become a double counting since they reproduce each other[1].
In the QCD sum rules for the traditional mesons,we usually introduce a parameter κ to parameterize the deviation from the factorization hypothesis by hand[26],for example,in the case of the four quark condensate,[26,27].In fact,the vacuum saturation works well in the large Nclimit[28].As the〉2is always companied with the finestructure constantand plays a minor important role,the deviation fromκ=1,for example,κ=2~3,cannot make much difference,though the valueκ>1 can lead to better QCD sum rules in some cases.
However,in the QCD sum rules for the tetraquark,pentaquark and hexaquark(molecular)states,the four-quark condensate plays an important role,a large value,for example,κ=2,can destroy the platforms in the QCD sum rules for the currentIn calculations,we observe that the optimal value isκ=1,the vacuum saturation works well in the QCD sum rules for the multiquark states.
Up to now,all the multiquark states are studied with the procedure illustrated in equations(5)–(10)by assuming the vacuum saturation for the higher dimensional vacuum condensates tacitly in performing the operator product expansion,except for in some case the parameter κ is introduced for the sake of fine-tuning[23].The true values of the higher dimensional vacuum condensates,even the four quark condensatesremain unknown or poorly known,where theΓand Γ′stand for the Dirac γ-matrixes,we cannot obtain robust estimations about the effects beyond the vacuum saturation.
In the QCD sum rules for the multiquark states,such as the tetraquark,pentaquark and hexaquark(molecular)states,we often encounter the vacuum condensatesandwe have the choice to introduce the parameter κ to parameterize the deviation from the factorization hypothesis,although the most commonly used valueκ=1 works well.If the true valueκ>1 or≫1,the QCD sum rules for the tetraquark,pentaquark and hexaquark(molecular)states have considerably larger systematic uncertainties and are less reliable than those of traditional mesons and baryons[29].In this respect,we make predictions for the multiquark masses with the QCD sum rules based on the vacuum saturation(i.e.κ=1),then confront them to the experimental data in the future to test the theoretical calculations.We can also choose the valueκ>1 and obtain predictions to be compared with the experimental data in the future.Many works are still needed to obtain the pertinent value of the κ.
We usually neglect the tadpole-like contributions from the contractions of the light quarks in the same currents in the QCD sum rules for the multiquark states.For the currentsandif we contract the light quarks in the same currents,we can obtain the following tadpole-like contributions,
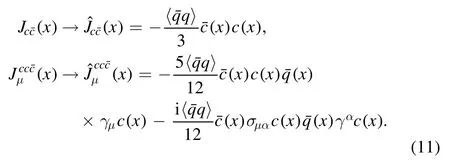
Now let us compute the integrals both in the coordinate space and momentum space in equations(5)–(8)to obtain the correlation functionsΠT(p2)andΠH(p2)at the quark-gluon level,and then obtain the QCD spectral densities through dispersion relation,
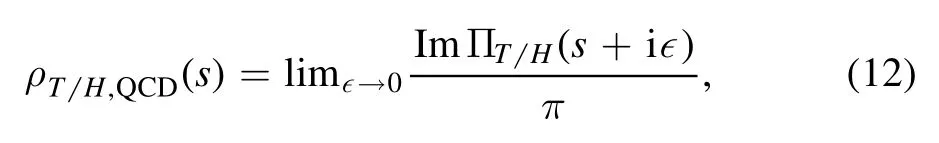
the QCD spectral densitiesρT,QCD(s)are given explicitly in the appendix,while the analytical expressions of the QCD spectral densitiesρH,QCD(s)are too cumbersome,the interested readers can contract me via E-mail to obtain them.
All the contributions in the operator product expansion can be shown explicitly using the Feynman diagrams.In the Feynman diagrams drawn in figures 1–5,we show the lowest order contributions.If we substitute the light and heavy quark lines with the full light and heavy quark propagators in equations(9)–(10),respectively,we can obtain all the Feynman diagrams.From the figures,we can see that there are only factorizable contributions in the color space for the currentsandwhile there are both factorizable and nonfactorizable contributions in the color space for the currents Jcc(x)andThere are also nonfactorizable sub-clusters in the Feynman diagrams for the currentsee the second and the third diagrams in figure 3.Thereafter,we will use the nomenclatures‘factorizable contributions’and‘nonfactorizable contributions’to denote the contributions come from the factorizable and nonfactorizable Feynman diagrams in the color space,respectively.
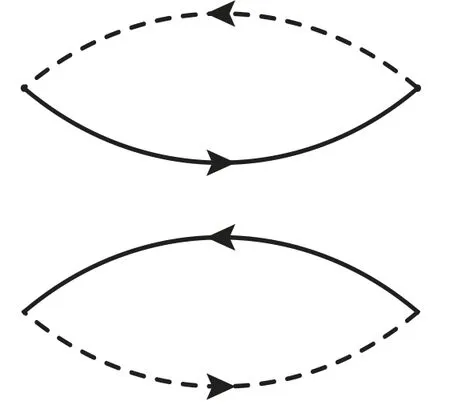
Figure 1.The Feynman diagram for the lowest order contribution for the current Jc c¯(x),where the solid lines and dashed lines represent the light quarks and heavy quarks,respectively.
From the factorizable diagrams,see figures 1 and 3–4,we can obtain both the factorizable and nonfactorizable diagrams,while from the nonfactorizable diagrams,see figures 2 and 5,we can obtain only the nonfactorizable diagrams.Lucha,Melikhov and Sazdjian assert that those nonfactorizable Feynman diagrams shown in figures 2 and 5 can be deformed into the box diagrams[12].It is unfeasible,those nonfactorizable Feynman diagrams can only be deformed into the box diagrams in the color space,not in the momentum space.
According to the assertion of Lucha,Melikhov and Sazdjian[11,12],the factorizable(disconnected)diagrams in the color space only make contributions to the meson–meson scattering states.From the lowest Feynman diagrams shown in figures 1–5,we can draw the conclusion tentatively that we can obtain more good QCD sum rules from the currents Jcc(x)andthan from the currentsandas there are connected(nonfactorizable)diagrams besides disconnected(factorizable)diagrams.
In fact,it is useless to distinguish the factorizable and nonfactorizable properties of the Feynman diagrams in the operator product expansion,where the short-distance contributions above a certain energy scale μ are included in the Wilson’s coefficients,the long-distance contributions below the special energy scale μ are included in the vacuum condensates.In general,we can choose any energy scales at which the perturbative QCD calculations are feasible.Besides the uncertainties originate from the energy scales,additional uncertainties come from the fact that it is impossible to separate the soft tails in the quark-loop diagrams using the standard Feynman-diagram technique.We cannot obtain the information asserted by Lucha,Melikhov and Sazdjian from the Feynman diagrams in the operator product expansion[11,12],we can only obtain information about the shortdistance and long-distance contributions.
We can borrow some ideas from the QCD sum rules for the conventional heavy mesons,in which the hadronic spectral densities can be written as,

where the subscript H denotes the D and B mesons,the fHare the decay constants,the hadronic spectral densities above the continuum thresholds s0are approximated by the perturbative contributions as only the perturbative contributions are left.In the operator product expansion,we often encounter the Feynman diagrams shown in figures 6–7,the Feynman diagrams shown in figure 6(figure 7)can be(cannot be)factorized into two colored quark lines.Analogously,could we assert that the Feynman diagrams shown in figure 6 can be exactly canceled out by two asymptotic quarks,only the Feynman diagrams shown in figure 7 make contributions to the heavy mesons?In[30],Lucha,Melikhov and Simula take into account all those Feynman diagrams,which is in contrast to the assertion of Lucha,Melikhov and Sazdjian in[11,12].
In the QCD sum rules for the tetraquark(molecular)states,pentaquark(molecular)states and hexaquark states(or dibaryon states),we take into account the vacuum condensates,which are vacuum expectations of the quark-gluon operators of the orderO(withk≤1 in a consistent way[8,13,24,31–35].

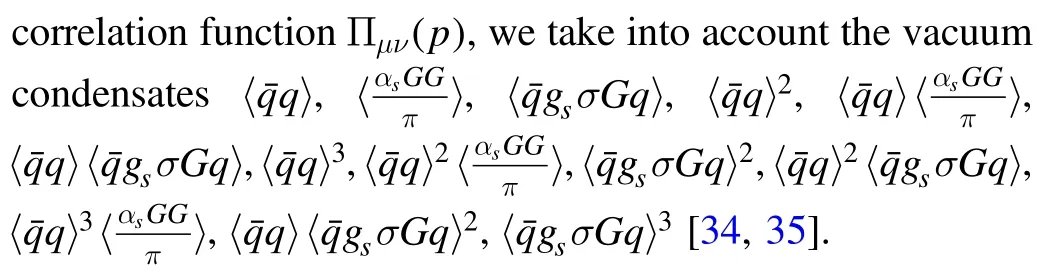
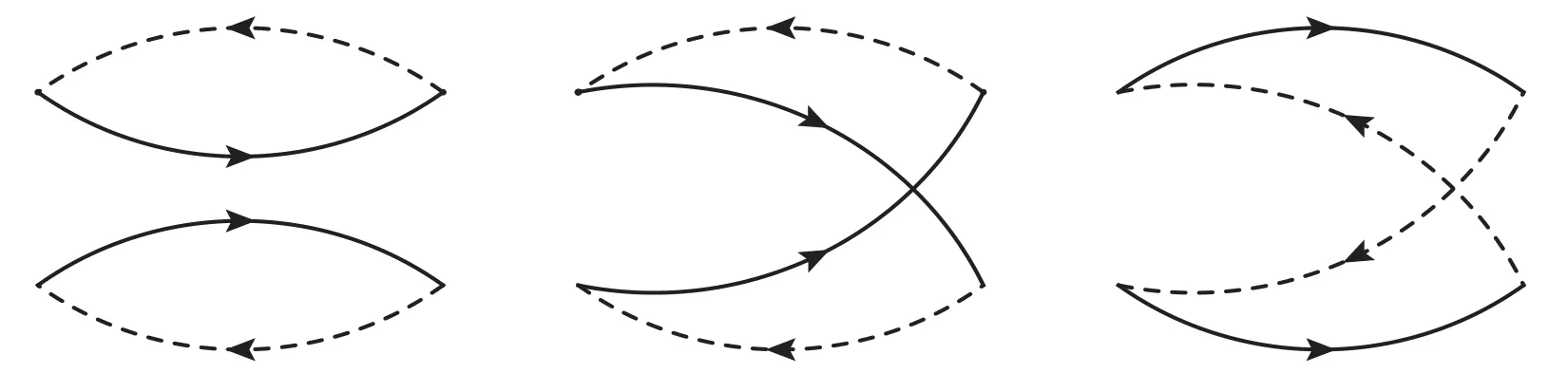
Figure 2.The Feynman diagrams for the lowest order contributions for the current Jcc(x),where the solid lines and dashed lines represent the light quarks and heavy quarks,respectively.
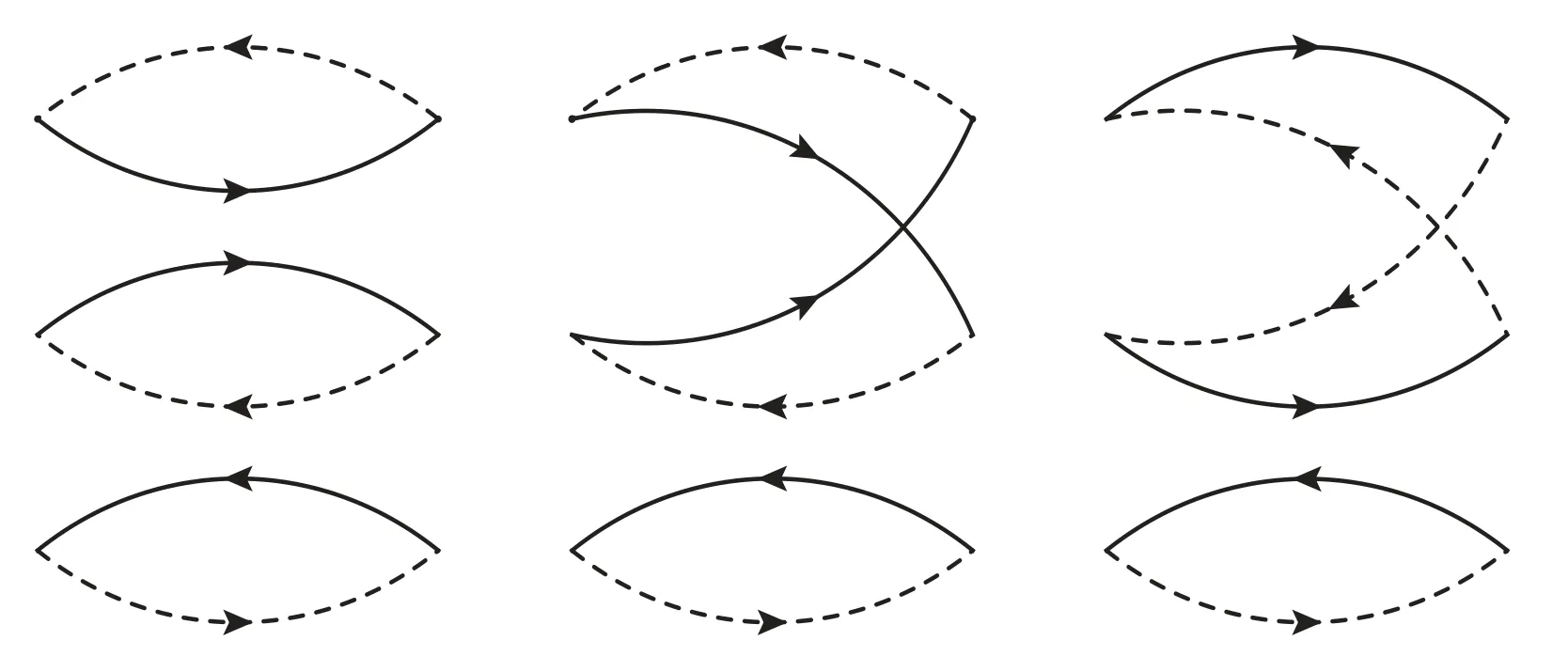
Figure 3.The Feynman diagrams for the lowest order contributions for the current where the solid lines and dashed lines represent the light quarks and heavy quarks,respectively.
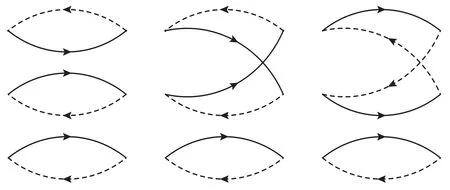
Figure 4.The factorizable Feynman diagrams in the color space for the lowest order contributions for the current ,where the solid lines and dashed lines represent the light quarks and heavy quarks,respectively.
Once the analytical expressions of the QCD spectral densities are obtained,we match the hadron side with the QCD side of the correlation functionsΠT(p2)andΠH(p2)below the continuum threshold s0and perform the Borel transform in regard toP2=-p2to obtain the QCD sum rules:
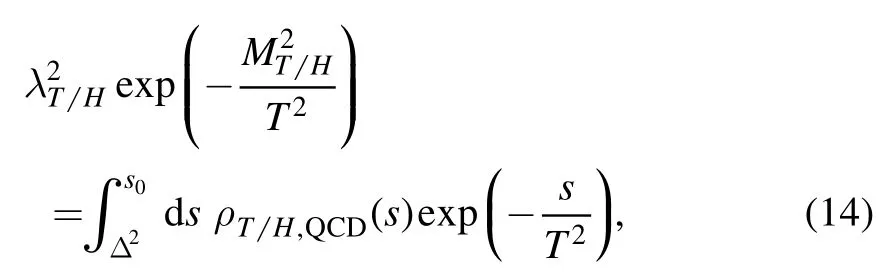
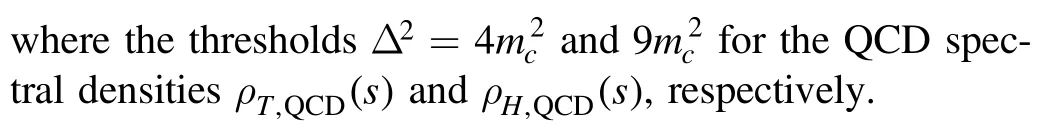
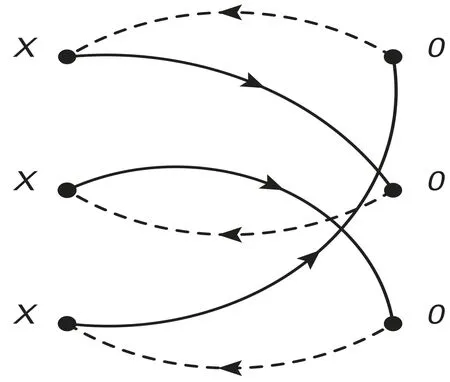
Figure 5.The nonfactorizable Feynman diagrams in the color space for the lowest order contributions for the current Jccc(x),where the solid lines and dashed lines represent the light quarks and heavy quarks,respectively,the other diagrams obtained by interchanging of the three vertexes at the point 0 or x are implied.
We differentiate equation(14)in regard tothen eliminate the pole residuesand obtain the QCD sum rules for the masses of the scalartetraquark molecular states and the vectorhexaquark molecular states,
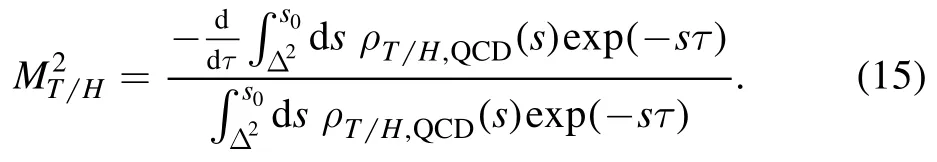
3.Numerical results and discussions

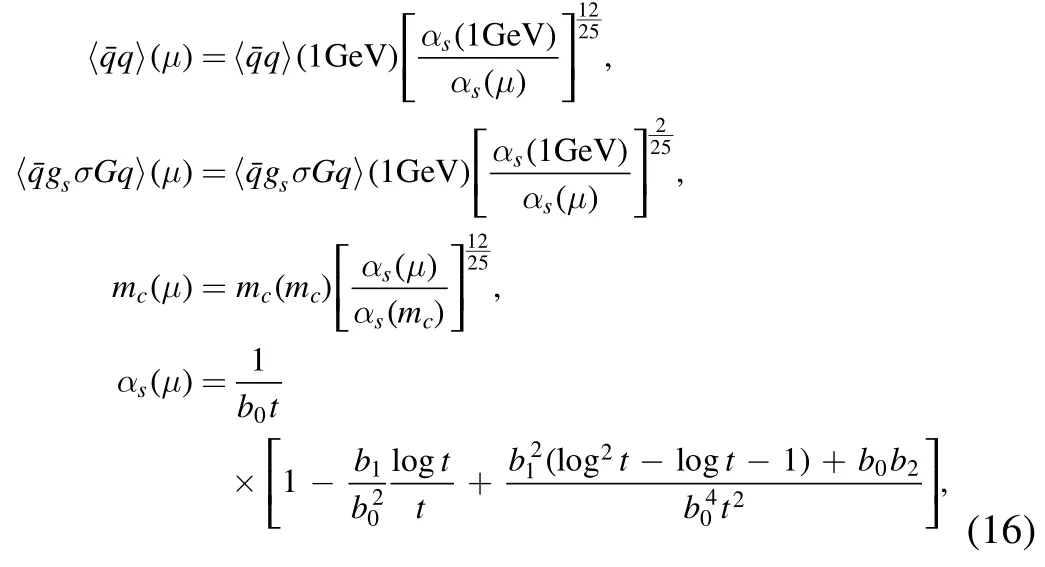
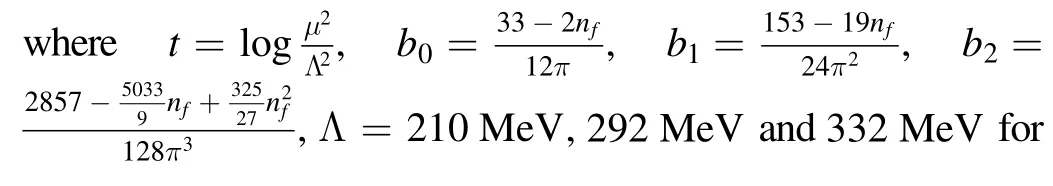

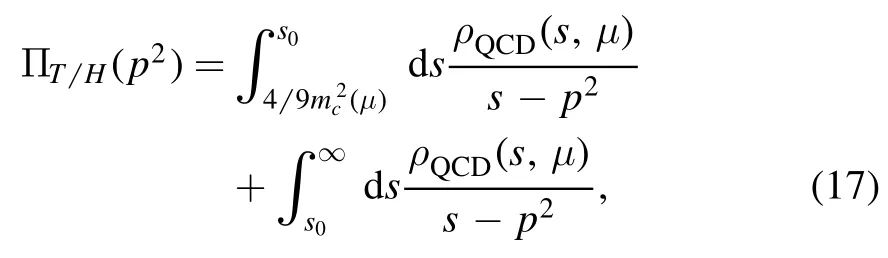
through dispersion relation at the QCD side,and they are scale independent or independent on the energy scale we choose to carry out the operator product expansion
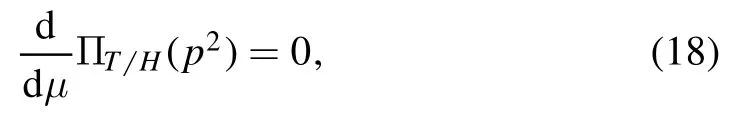
which does not mean
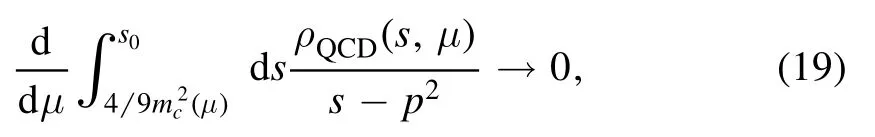
due to the two features inherited from the QCD sum rules:
•Perturbative corrections are neglected,even in the QCD sum rules for the traditional mesons,we cannot take into account the perturbative corrections up to arbitrary orders;the higher dimensional vacuum condensates are factorized into lower dimensional ones based on the vacuum saturation,therefore the energy scale dependence of the higher dimensional vacuum condensates is modified.
•Truncations s0set in,the correlation between the thresholdand continuum threshold s0is unknown.
After performing the Borel transform,we obtain the integrals
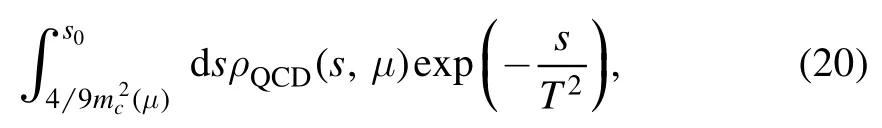
which are sensitive to the c-quark massmc(μ)or the energy scale μ.Variations of the energy scale μ can lead to changes of integral rangesof the variable ds besides the QCD spectral densitiesρQCD(s,μ),therefore changes of the Borel windows and predicted masses and pole residues.
Although we cannot obtain the QCD sum rules independent on the energy scales of the QCD spectral densities,we have an energy scale formula to determine the pertinent energy scales consistently.In this article,we study the color-singlet-color-singlet type tetraquark molecular states and color-singlet-color-singlet-color-singlet type hexaquark molecular states,which have two charm quarks and three charm quarks,respectively.Such two-c-quark and three-cquark systems are characterized by the effective charmed quark mass or constituent quark massMcand the virtualityWe set the energy scales of the QCD spectral densities to beμ~V,and obtain the energy scale formula
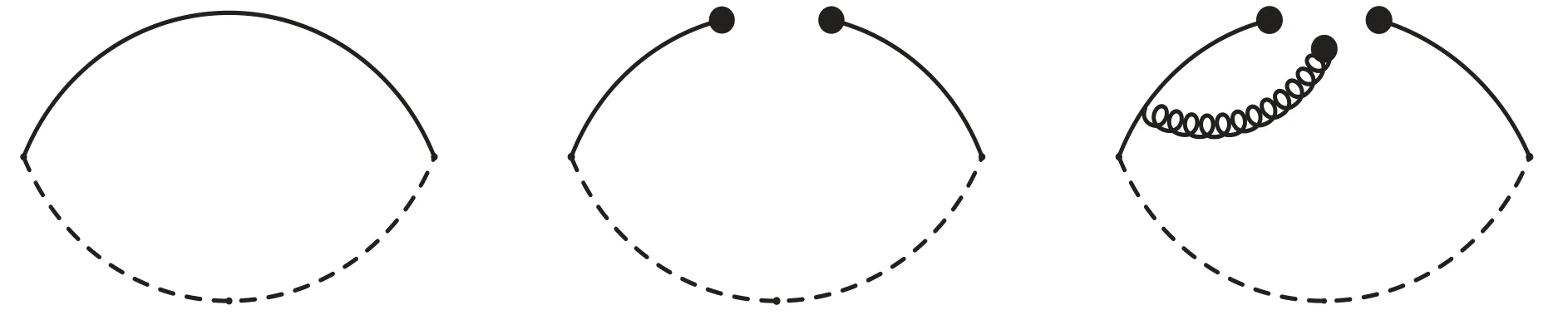
Figure 6.The typical Feynman diagrams which can be factorized into two colored quark lines for the conventional heavy mesons,where the solid line and dashed line denote the light quark and heavy quark,respectively.
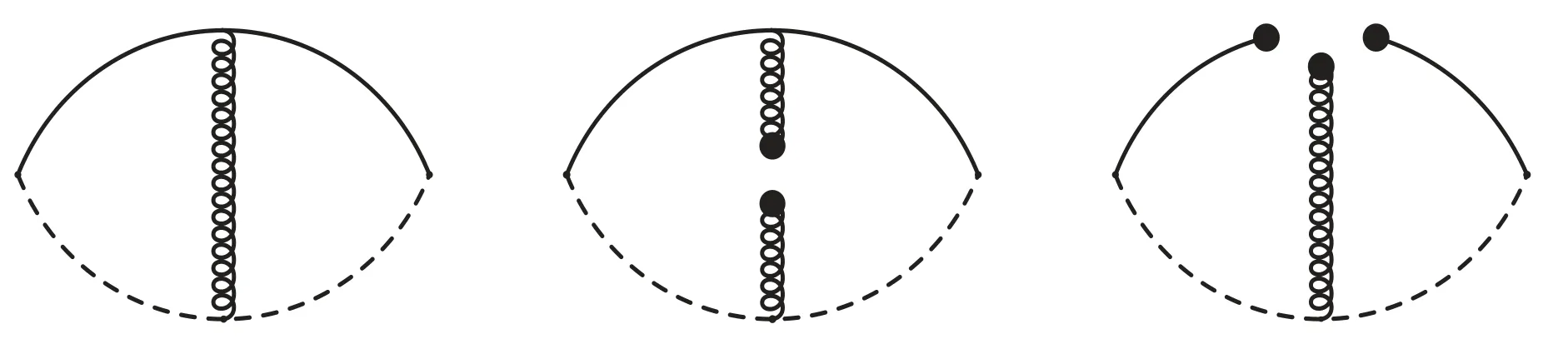
Figure 7.The typical Feynman diagrams which cannot be factorized into two colored quark lines for the conventional heavy mesons,where the solid line and dashed line denote the light quark and heavy quark,respectively.


We can rewrite the energy scale formula in the following form,
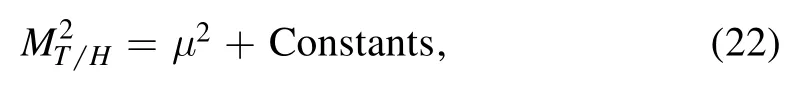
where the Constants have the valuesorAs we cannot obtain energy scale independent QCD sum rules,we conjecture that the predicted multiquark masses and the pertinent energy scales of the QCD spectral densities have a Regge-trajectory-like relation,see equation(22),where the Constants are free parameters and fitted by the QCD sum rules.Direct calculations have proven that the Constants have universal values and work well for all the tetraquark and hexaquark molecular states.At the beginning,we do not know the values of the mulitquark masses,we choose the energy scaleμ=1.0 GeV tentatively,then optimize the continuum threshold parameters and Borel parameters to obtain the predictionsif they do not satisfy the relationthen we set the energy scaleμ=1.1 GeV,1.2 GeV,1.3 GeV,…tentatively,and repeat the same routine until reach the satisfactory results.
Such a routine can be referred to as trial and error,we search for the best continuum threshold parameters s0and Borel parameters T2via trial and error to satisfy the two basic criteria of the QCD sum rules,the one criterion is pole dominance at the hadron side,the other criterion is convergence of the operator product expansion at the QCD side.Firstly,let us define the pole contributionsPC
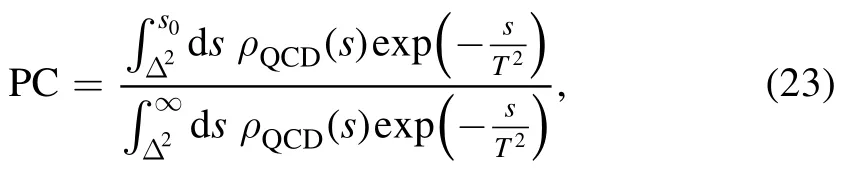
and define the contributions of the vacuum condensates of dimension n,
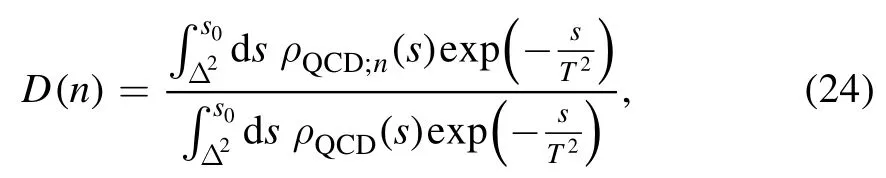
where theρQCD;n(s)are the QCD spectral densities containing the vacuum condensates of dimension n.For the hexaquark(molecular)states,the largest powerρH,QCD(s)∝s7,while for the tetraquark(molecular)states,the largest powerρT,QCD(s)∝s4,it is very difficult to satisfy the two basic criteria of the QCD sum rules simultaneously,we have to resort to some methods to improve the convergent behaviors of the operator product expansion and enhance the pole contributions,the energy scale formula does the work.


Table 1.The Borel parameters,continuum threshold parameters,energy scales of the QCD spectral densities and pole contributions for the D **,D D**,D*D**and D*DD**tetraquark and hexaquark molecular states.
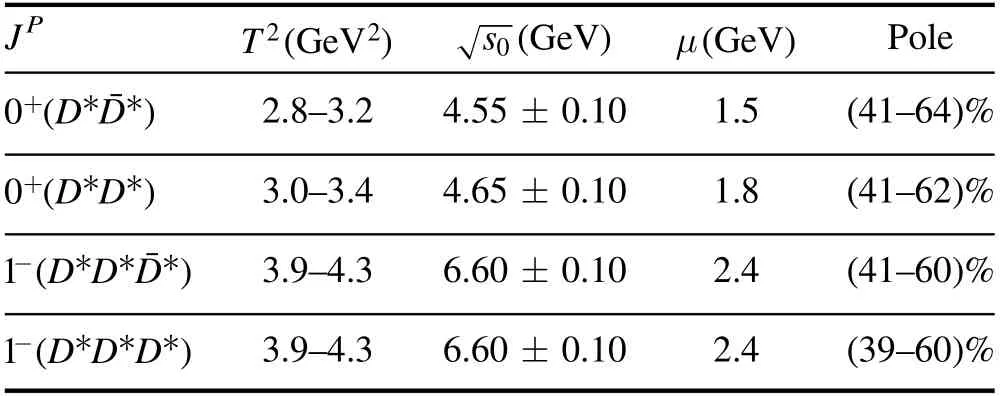
Table 1.The Borel parameters,continuum threshold parameters,energy scales of the QCD spectral densities and pole contributions for the D **,D D**,D*D**and D*DD**tetraquark and hexaquark molecular states.
JPT 2GeV2()s GeV 0()μ(GeV)Pole+D D 0**(¯)2.8–3.24.55±0.101.5(41–64)%+D D 0(**)3.0–3.44.65±0.101.8(41–62)%-D D D 1***(¯)3.9–4.36.60±0.102.4(41–60)%-D D D 1***()3.9–4.36.60±0.102.4(39–60)%
After trial and error,we obtain the best continuum threshold parameters,Borel parameters,energy scales of the QCD spectral densities,and thereafter the pole contributions,which are shown explicitly in table 1.From the table,we can see that the pole contributions are about(40%–60)%,the pole dominance criterion is well satisfied.
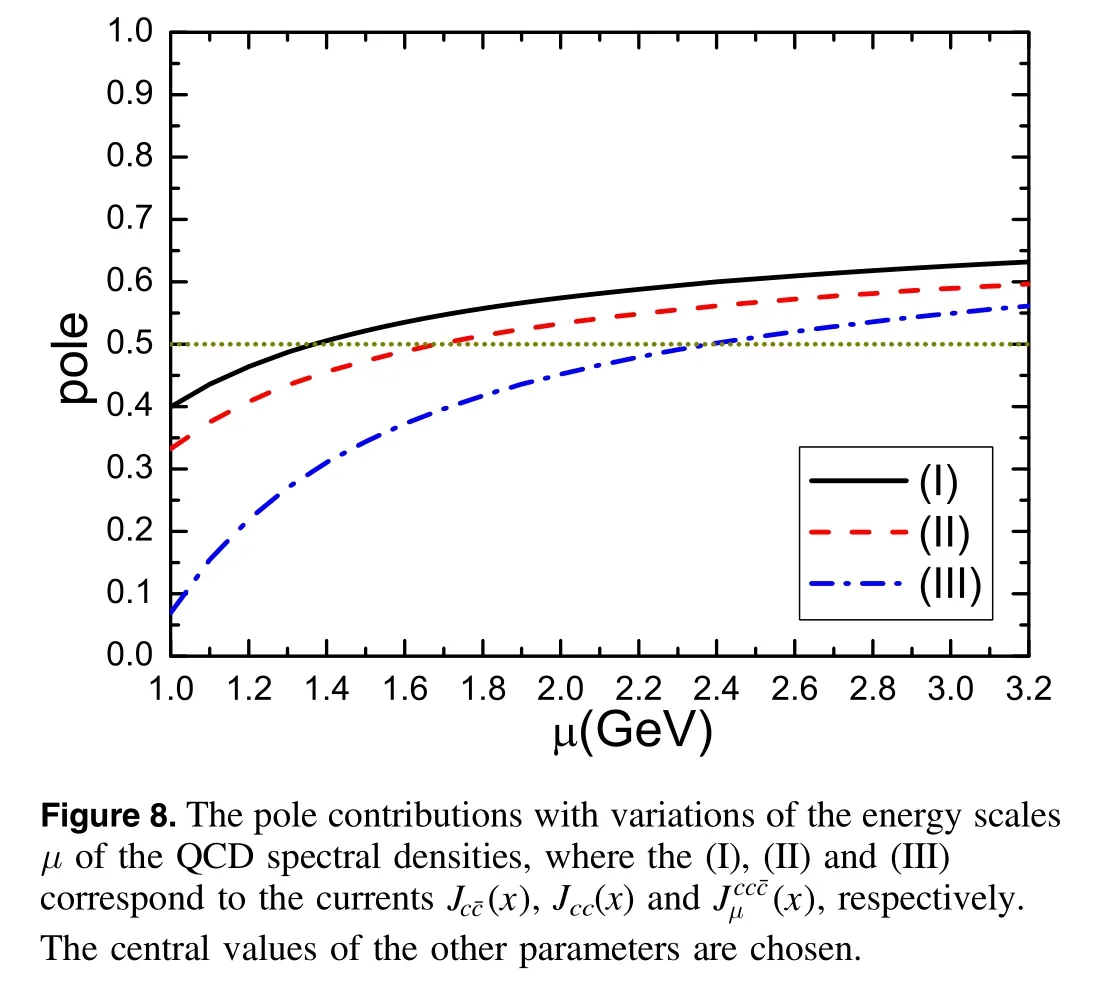
In figure 8,we plot the pole contributions with variations of the energy scales μ of the QCD spectral densities for the currentsandwith the central values of other input parameters shown in table 1.From the figure,we can see that the pole contributions increase monotonically and quickly with the increase of the energy scales of the QCD spectral densities before reaching 50%,then they increase monotonically but slowly.The pole contributions exceed 50%at the energy scalesμ=1.5 GeV,1.8 GeV and2.4 GeV for the currentsandrespectively.The energy scale formula shown in equation(21)plays a very important role in enhancing the pole contributions.
In figure 9,we plot the absolute values of the contributions of the vacuum condensates for the central values of the input parameters shown in table 1 under the condition that the total contributions are normalized to be 1.From the figure,we can see that although the perturbative terms cannot make the dominant contributions,the operator product expansions have very good convergent behaviors.The largest contributions come from the vacuum condensateswhich serve as a milestone,the contributions of the vacuum condensates D(n)decrease quickly with the increase of the dimension n except for some vibrations due to the tiny contributions D(4),D(7)and large contributions D(6).The contributions of the vacuum condensateswhich are of dimension 4 and 7 respectively,play a minor important role.For the currentsand∣D(6)∣>∣D(5)∣.
In figure 10,we plot the predicted masses of theD D*¯*,D D**andD**tetraquark and hexaquark molecular states with variations of the energy scales μ of the QCD spectral densities,where we have taken the central values of the input parameters.On the other hand,we can rewrite the energy scale formulas as
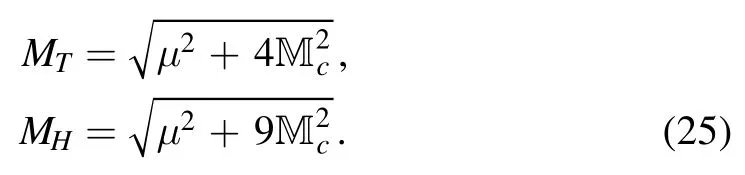
If we setMc=mc=1.84 GeV,we can obtain the dash-dotted linesandin figure 10,which intersect with the lines of the masses of the**,D D**andD**tetraquark or hexaquark molecular states at the energy scales aboutμ=1.5 GeV,1.8 GeV and2.4 GeV,respectively.In this way,we choose the energy scales of the QCD spectral densities in a consistent way.
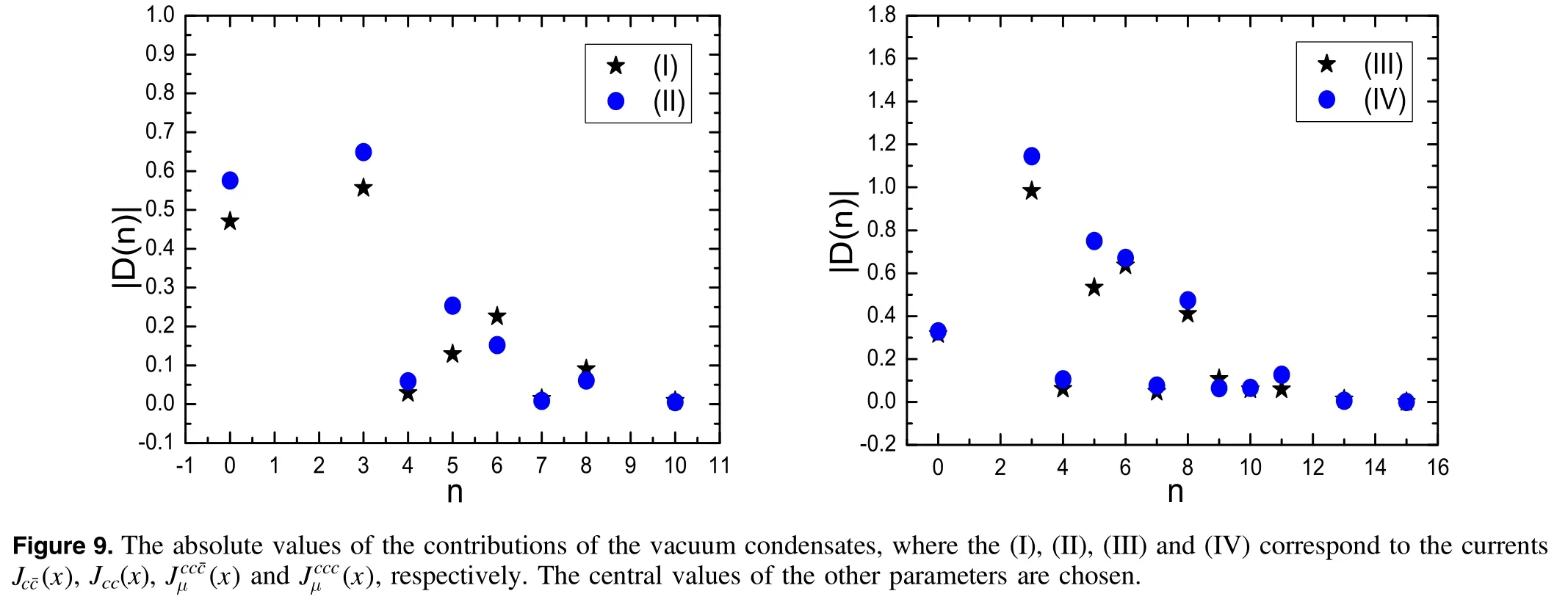
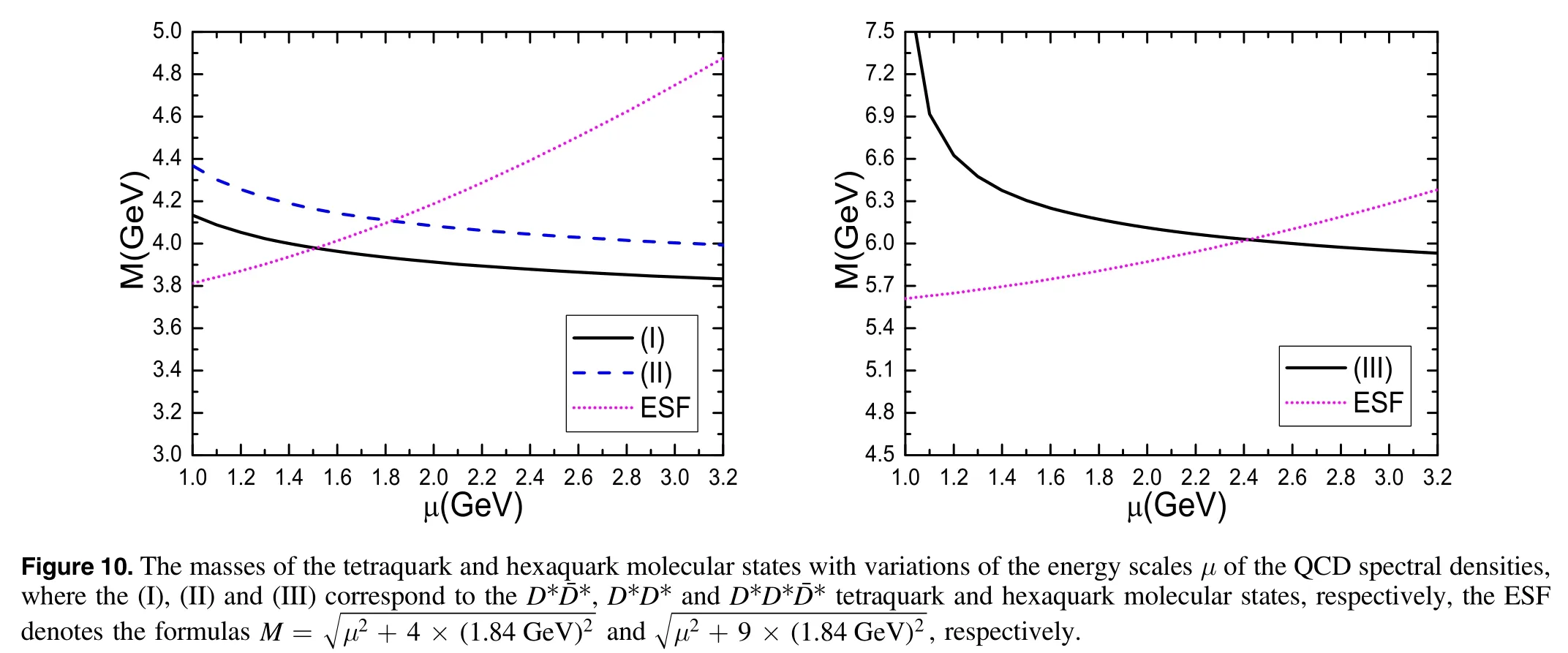
Table 2.The masses and pole residues for the D *,D D**and D*D*tetraquark and hexaquark molecular states.

Table 2.The masses and pole residues for the D *,D D**and D*D*tetraquark and hexaquark molecular states.
JP MT H λT H+D D 0(*¯*)3.98±0.09 GeV±×-4.05 0.7010 2GeV5()+D D 0(**)4.11±0.09 GeV±×-8.36 1.3210 2GeV5()-D D D 1***(¯)6.03±0.11 GeV±×-3.14 0.5510 3GeV8()
In this article,we choose the value of the effective cquark massMc=1.84 ±0.01 GeV [13],which leads to a uncertaintyδμ=±0.1 GeV for the QCD spectral densities.Now we take into account all uncertainties of the input parameters,and obtain the values of the masses and pole residues of the*,D D**andD**tetraquark and hexaquark molecular states,which are shown explicitly in table 2 and figure 11.
From figure 11,we can see that there appear flat platforms in the Borel windows for the*D D**andD**molecular states,it is reliable to extract the tetraquark and hexaquark molecular state masses.We can search for the scalar*,D D**tetraquark states and the vectorD**hexaquark molecular state at the LHCb,Belle II,CEPC,FCC,ILC in the future.
We can take into account the contributions of the intermediate two-meson and three-meson scattering states to the correlation functionsΠT(p2)andΠH(p2)according to the arguments presented in[13,24,43],as the currentsandalso couple potentially to the*D D**,D**andD*DD**scattering states respectively according to the standard definition,
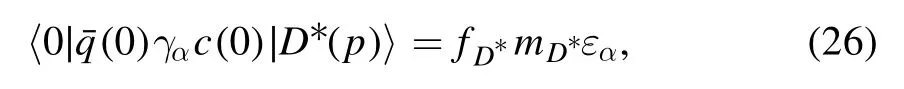
where theεαis the polarization vector of the D*meson.The renormalized self-energies due to the intermediate mesonloops contribute a finite imaginary part to modify the dispersion relation,
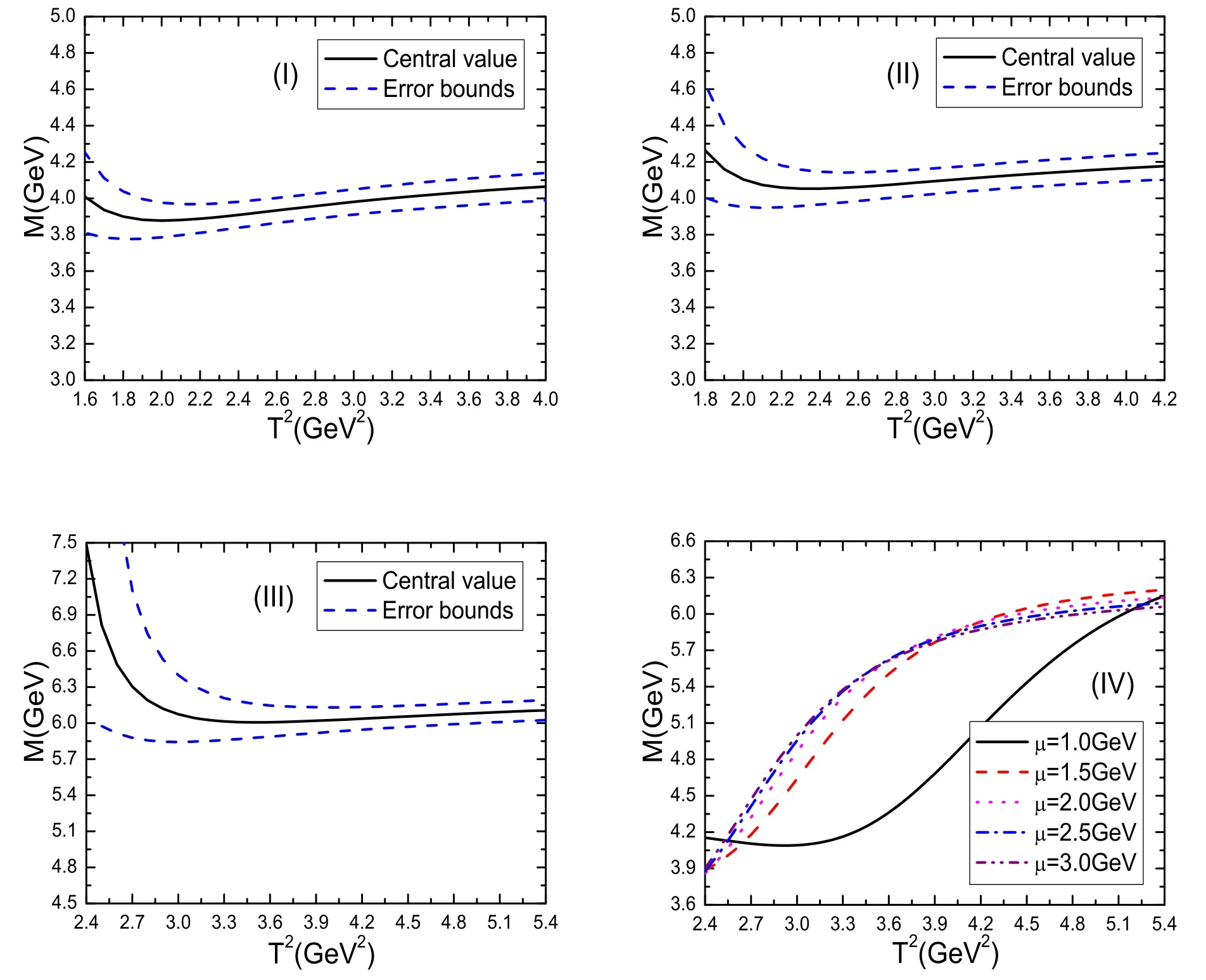
Figure 11.The masses of the tetraquark and hexaquark molecular states with variations of the Borel parameters T2,where the(I),(II),(III)and(IV)correspond to the D *,D D**,D*D*and D*DD**tetraquark and hexaquark molecular states,respectively.
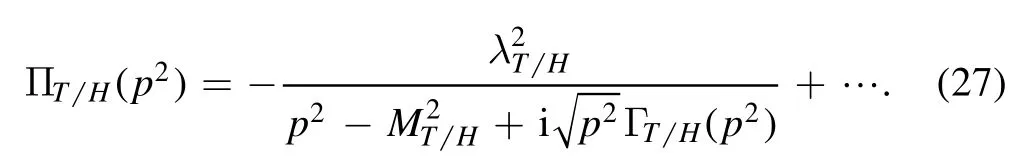
We take into account the finite width effects by the following simple replacement of the hadronic spectral densities,
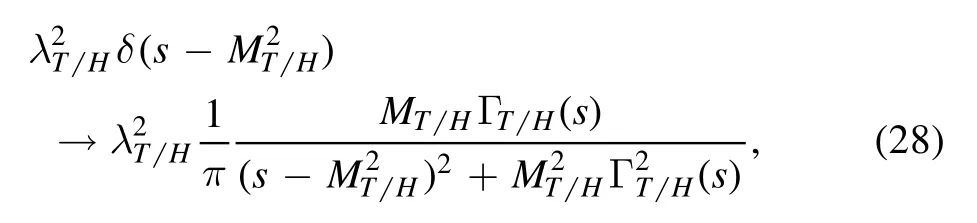
then the hadron sides of the QCD sum rules in equations(14)–(15)undergo the following changes

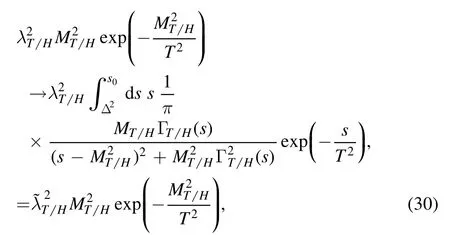
where theΔ2are the two-meson or three-meson thresholds.The net effects of the intermediate meson-loops can be absorbed into the pole residuessafely without affecting the predicted tetraquark and hexaquark molecule masses.Even for theZc(4200),the width is as large asthe finite width effects can be safely absorbed into the pole residues[43],so the zero width approximation in the hadronic spectral density works very well.
In figure 11,we also plot the predicted masses of theD*DD**hexaquark molecular state with variations of the Borel parameters T2at the energy scales of the QCD spectral densitiesμ=1.0 GeV,1.5 GeV,2.0 GeV,2.5 GeV and 3.0 GeV.From the figure,we can see that there appear no platforms for theD*DD**hexaquark molecular state.The QCD sum rules do not support the existence of theD*DD**hexaquark molecular state with theJP=1-.
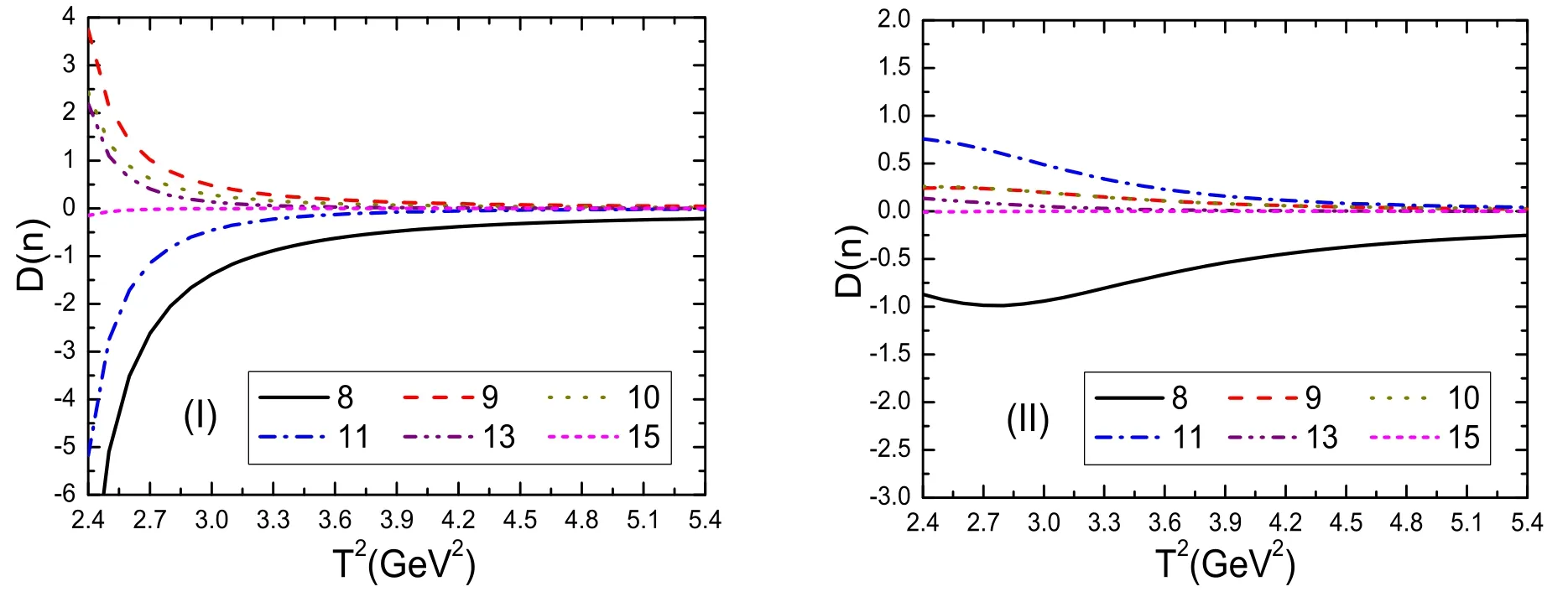
Figure 12.The contributions of the higher dimensional vacuum condensates with variations of the Borel parameters T2 for the central values of other parameters,where the(I)and(II)correspond to the currents and,respectively.
From figures 1–2,we can see that compared to the currentthere are connected(nonfactorizable)Feynman diagrams in the correlation functionΠ(p)for the current Jcc(x)besides the disconnected(factorizable)Feynman diagrams.The connected diagrams and other diagrams obtained by substituting the quark lines with other terms in the full light and heavy propagators lead to more stable QCD sum rules for the predicted mass of theD D**tetraquark molecular state,see figure 11.From figures 3–5,we can see that compared to the currentthere are connected Feynman diagrams in the correlation functionΠμν(p)for the current Jccc(x)besides the disconnected Feynman diagrams.The contributions from the connected diagrams and other diagrams obtained by substituting the quark lines with other terms in the full light and heavy propagators are so large as to make the QCD sum rules for the mass of theD*DD**hexaquark molecular state unstable,see figure 11.
In summary,the connected Feynman diagrams at the tree level shown in figure 2 and their induced diagrams via substituting the quark lines make positive contributions,the connected Feynman diagrams at the tree level shown in figure 5 and their induced diagrams via substituting the quark lines make negative or destructive contributions,which are in contrast to the assertion of Lucha,Melikhov and Sazdjian that the factorizable(disconnected)diagrams in the color space only make contributions to the meson–meson scattering states,the tetraquark molecular states begin to receive contributions from the nonfactorizable(connected)diagrams at the orderO[11,12].In fact,it is of no use to distinguish the factorizable and nonfactorizable properties of the Feynman diagrams in the color space.
In figure 12,we plot the contributions of the vacuum condensates D(n)withn≥8 for theandwith the central values of the input parameters shown in table 1.From the figure,we can see that,for the currentthe contributions of the higher dimensional vacuum condensates are huge for the small Borel parameters T2,and decrease monotonously and quickly with the increase of the Borel parameters T2at the regionT2≤3.6 GeV2,then they decrease monotonously and slowly with the increase of the Borel parameters T2.The higher dimensional vacuum condensates play a minor important role in the Borel windows,but they play a very important role in determining the Borel windows or in warranting the appearances of the Borel platforms While for the current(x),the contributions of the higher dimensional vacuum condensates are not greatly amplified for the small Borel parameters T2,and decrease monotonously and slowly with the increase of the Borel parameters T2,which cannot stabilize the QCD sum rules to obtain reliable predictions,the QCD sum rules at the hadron side may be dominated by the three-meson scattering states.
4.Conclusion
In this article,we construct the color-singlet-color-singlet type currents and the color-singlet-color-singlet-color-singlet type currents to interpolate the scalar*,D D**tetraquark molecular states and the vectorD**,D*DD**hexaquark molecular states,respectively,and study their masses and pole residues with the QCD sum rules in details by carrying out the operator product expansion up to the vacuum condensates of dimension 10 and dimension 15,respectively.In calculations,we choose the pertinent energy scales of the QCD spectral densities with the energy scale formulaandfor the tetraquark molecular states and hexaquark molecular states respectively in a consistent way,which can enhance the pole contributions remarkably and also improve the convergent behaviors of the operator product expansion remarkably.We obtain stable QCD sum rules for the masses and pole residues of the scalar*,D D**tetraquark molecular states and the vectorD**hexaquark molecular state,but cannot obtain stable QCD sum rules for the vectorD*DD**hexaquark molecular state.We can search for the*,D D**andD**tetraquark and hexaquark molecular states at the LHCb,Belle II,CEPC,FCC,ILC in the future.In calculations,we observe that the connected Feynman diagrams at the tree level and their induced diagrams via substituting the quark lines make positive contributions in the QCD sum rules for theD D**tetraquark molecular state,but make negative or destructive contributions in the QCD sum rules for theD*DD**hexaquark molecular state,where the tree level denotes the lowest order contributions shown in figures 1–5.Lucha,Melikhov and Sazdjian assert that those nonfactorizable Feynman diagrams shown in figure 2 and figure 5 can be deformed into the box diagrams.It is unfeasible,those nonfactorizable Feynman diagrams can only be deformed into the box diagrams in the color space,not in the momentum space.It is of no use or meaningless to distinguish the factorizable and nonfactorizable properties of the Feynman diagrams in the color space in the operator product expansion so as to interpret them in terms of the hadronic observables,we can only obtain information about the short-distance and longdistance contributions.
Acknowledgments
This work is supported by National Natural Science Foundation,Grant Number 11 775 079.
Appendix




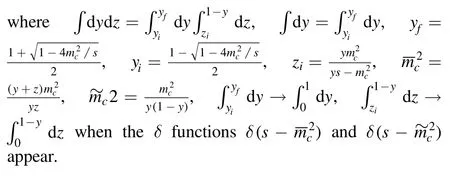
 Communications in Theoretical Physics2021年6期
Communications in Theoretical Physics2021年6期
- Communications in Theoretical Physics的其它文章
- Intermediate symmetric construction oftransformation between anyon and Gentile statistics
- Proton radioactivity within the generalized liquid drop model with various versions of proximity potentials
- Joule–Thomson expansion of higher dimensional nonlinearly AdS black hole with power Maxwell invariant source
- Notch fatigue of Cu50Zr50 metallic glasses under cyclic loading:molecular dynamics simulations
- Eigen microstates and their evolutions in complex systems
- Non-similar mixed convection analysis for magnetic flow of second-grade nanofluid over a vertically stretching sheet
