锂离子电池健康状态评估方法研究进展

李肖辉，陈北海，古领先，王 京，魏小锋

(许继集团有限公司许昌许继电科储能技术有限公司，河南许昌 461000)

电化学储能是电力系统中非常重要的一环，其广阔的应用场景，如新能源配套、调峰调频、峰谷套利、黑启动、其他辅助服务等，使其以爆发式的速度增长。仅在2018 年，中国累计装机容量1.07 GW，同比增加175.2%；全球累计装机容量达6.6 GW，同比增长126.3%。但全球电化学储能占比仅为2.47%，发展空间非常广阔。电化学储能所使用的电池包括液流电池、锂离子电池、铅蓄电池、金属空气电池等。目前在总装机容量上铅蓄电池占主导地位，但在2018 年新增电化学储能装机容量，锂离子电池占比达到76%，处于绝对领先位置。2019 年仅在电源侧我国装机容量为855 MW。预计到2021 年，我国电化学储能装机规模达到近11 GW；到2024 年，达到近30 GW；到2035 年年底，我国电化学储能装机容量达到近200 GW[1-4]。

锂离子电池相比于铅酸蓄电池在耐用性、成本价格、充放电性能及环保方面均具有一定的优越性。这其中磷酸铁锂电池以综合性能优异(如循环寿命长、安全性能高等)成为电化学储能的主流电池。相比于三元电池能量密度的劣势，储能在空间上并不像电动汽车那么迫切追求高能量密度。最近几年磷酸铁锂电池在储能电站实际应用中，一般的放电深度为80%，高的达到90%，并且不全是简单的削峰填谷、满功率充放的运行方式，而是更多的MW 级别调频，一天之内变换充放方向数千次[5-7]。

电池的健康状态(SOH)对电站的正常运行寿命、电站经济性、安全性及精准预测剩余容量(state of charge，SOC)具有决定性作用及指导性意义[8]。影响电池SOH的主要因素可以分为内部因素和外部因素两种：外部因素主要涉及充放电电流大小、电池工作温度、工作截止电压、电池成组一致性等指标；内部因素主要包括电池所用原材料、制备工艺、电池内部老化等[9-10]。本文对近阶段SOH预估方法研究进展进行了综述，以此来更好地服务于储能电站的建设发展。

1 SOH 影响因素

影响锂离子电池SOH的因素有很多，大体上可以分为外部因素和内部因素两种，受影响因素的主要外在结果表现为锂离子电池电化学性能下降，如平台期缩短造成容量衰减、电化学极化变大、静态电压回升能力下降等。同时会造成电池系统的整体能量迅速衰减，电池系统DOD变小、在BMS 保护阈值下告警增多等性能及安全上的隐患[11]。

1.1 工作环境的影响

锂离子电池对工作环境的要求很高，如磷酸铁锂电池在低温环境中容量会大打折扣，若长期处于高温环境中，则又加速电池老化，对电池循环寿命造成影响。文献[12]的实验结果表明，高温是导致电池容量衰退、健康度下降的主要因素；文献[13]在25 和40 ℃条件下，对循环后的电池电极材料进行SEM、XRD 和FTIR 分析，结果表明容量衰退主要归因于负极SEI 膜持续消耗Li+以及正极处发生不可逆的副反应所致；文献[14]中对电池进行不同截止电压和不同温度的浮充实验，结果发现温度每增加15 ℃或者浮充截止电压每增加0.1 V 时，电池寿命大约减少一半。

1.2 放电深度(depth of discharge，DOD)的影响

锂离子电池在充放电平台区间工作的话，可以适当延长电池使用寿命，并且可以增强使用过程中的安全性能[15]。无论应用在电动汽车还是大规模储能当中，安全均是第一位的。在大规模储能系统中，DOD大致有10%～90%、15%～90%、15%～85%等几个区间，主要根据业主要求以及电池厂家来决定。若DOD过大，可能会造成某节单体电芯过充过放的风险，长时间处于这一种状态下，会严重影响电池系统的使用寿命。另外，由于电池系统的木桶效应，当其中某一节电池出现问题时，整个电池系统的电量势必会受到影响[16]。若DOD过小，则会影响到电池系统整体出力，不能够满足业主要求，造成业主收益损失。

1.3 使用工况的影响

在一定的使用环境、放电深度及电池管理系统(battery management system，BMS)保护阈值设定下，电池以何种工况运行是一个值得考虑的问题[17]。电池在设计生产时，通常有一个标称容量，但是在涉及到循环寿命时，就会出现一系列问题，需要按国家标准以一定倍率、一定方式进行循环寿命测试。在实际应用中，电池系统运行方式是否一直沿用一种模式，还是几种模式交替使用，都是必须要考虑的因素。是短时间内快速浅充浅放对电池的损耗大，还是满功率的满充满放对电池系统损耗大，对电池的健康状态及系统的使用寿命都能产生很大的影响。

为了使电池能够处在良好的工作状态，对电池健康状态SOH的估计是必不可少的。文献[18]对电池进行循环寿命实验，建立了基于恒流充电阶段电压曲线的SOH估计模型，然后利用此曲线对SOH进行估计。文献[19]提出了一种基于电池衰减模式量化电极在电池中衰减行为的方法，通过建立状态诊断模型，然后模拟电池充放电曲线，分析电池在老化过程中的状态变化，对电池当前所处的健康状态作出判断，此种估计方法更为简单。文献[20]建立了基于主成分回归的容量估计模型估算电池SOH值，该方法既可以判断出电池当前所处的健康状态，又能够识别电池的老化模式，为今后电池寿命管理系统(BMS)的研究提供依据，有较大的参考价值。

锂离子电池健康状态预测方法大体上可以分为实验估计法、自适应滤波法和数据驱动法三大类[21]。实验估计法包括容量测量法、电阻测量法、差分分析法等[22]；自适应滤波法包括卡尔曼滤波法、粒子滤波法、最小二乘法等[23]；数据驱动法包括人工神经网络算法、支持向量机法、智能优化算法等[24]。本文提取了国内外的三篇研究成果进行仔细分析研究，希望能为同行们的研究及行业发展起到一定的推动作用。

2 线性预测误差方法(L-PEM)

预测误差方法(prediction error methods,PEM)是一系列广泛的参数估计方法，可应用于相当任意的模型参数化[25-26]。例如，给定x(t−1),x(t−2),…,x(t−M)，我们预测x(t)的值。一般情况下，该预测值表示为给定的M个过去样本的函数：

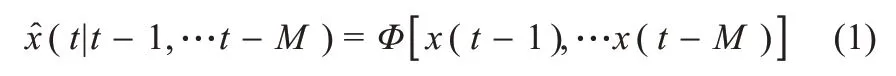
在式(1)中，式左侧表示输出的一步预测，并且Φ是过去观察到数据的任意函数。如果我们假设Φ是线性函数，那么可以说预测是线性PEM。可以表示为：

如果我们假设最后一个数据集是M个先前数据集的线性组合，那么我们的目标是找到作为矢量系数的qk。这些系数qk可以通过预测输出和测量输出x(i)之间的最小距离来找到。

在式(3)中，所有的求和内容为合适的距离度量值。式(3)给出最大似然估计的结果，而最小化参数的实际计算很复杂，需要对具有多个局部最小值的函数进行复杂的搜索。PEM 系列具有可应用于多种模型结构的优势[27]。该方法在用于建立电池健康状态预测的线性模型外，还可根据其模型预测剩余使用寿命(remaining useful life,RUL)。

图1 为使用该方法与实际测量的容量数据结果对比图。从图中可以看出，使用该模型的预测曲线与实际曲线基本吻合，对电池健康状态预估的准确性，具有一定的参考价值。

图1 使用PEM的容量估计

3 粒子群结合BP 神经网络法

3.1 粒子群算法流程

粒子群算法也叫做鸟群觅食法，简写为PSO(particle swarm optimization)，该算法属于进化算法，以随机的解为起点，通过不断迭代寻找最优目标解[28]。粒子群算法流程如下：

(1)随机初始化一个粒子群(数量为p)，其中第i个粒子在n维空间中的位置可以表示为Xi={xi1,xi2,…xi n}，其速度为Vi={vi1,vi2,…vi n}；

(2)在每次迭代过程中，粒子通过两个极值来更新自己的速度和位置：一个是单个粒子从初始状态到当前迭代次数搜索产生的最优解，称为个体极值Li={li1,li2,…li n}；另一个是种群目前的最优解，称为全局最优解Gi={gi1,gi2,…gi n}[29]。定义适应度函数如式(4)所示：

式中：R为观测噪声方差；yk为当前时刻观测量；ypred为预测观测量。粒子群算法通过计算适应度值将所有的粒子向全局最优粒子移动，从而得到全局最优解。

粒子群优化算法(PSO)参数单一，结构简单，根据速度和位置即可获得全局最优解。BP 神经网络是基于信号前向传播和误差反向传播过程的算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小[30]。图2 为PSO 算法与BP 神经网络相结合的算法流程图。首先从给定的输入、输出参数确定其结构，根据计算公式得出其适应度值，最后由不断更新的粒子速度和位置寻找出全局最优解。

图2 粒子群优化神经网络算法流程图

3.2 结果分析

在MATLAB 上分别对BP 神经网络算法和PSO-BP 算法进行建模，在实际测试中以特定的工况对某厂家正常电池进行测试。模型仿真分析分别为预测与实测结果对比、绝对误差及相对误差对比，分别由图3、4、5 表示。

从图3 可以看出，PSO-BP 和BP 的预测值与测试值都非常接近，均可以对电池SOH有较好的预估。进一步看来，PSO-BP 神经网络的预测模型输出数据曲线与参考值有更好的逼近效果。

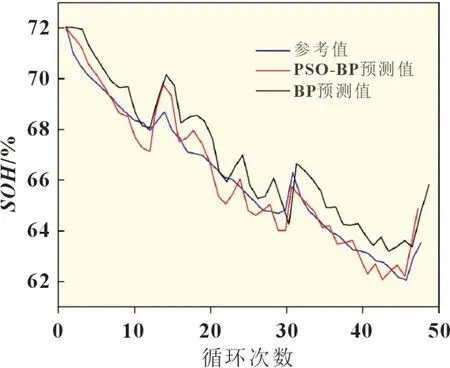
图3 两种算法的SOH预测结果对比图

从图4 可以得出，BP 与PSO-BP 网络模型的预测误差分别保持在2.5%与1.6%之内，其中BP 网络模型误差变化主要集中在[0,2%]，PSO-BP 网络模型误差变化相对较小，主要集中在[－1%，1%]。

图4 两种算法的绝对误差结果对比图

根据图5 可以得出，BP 网络模型的相对误差均小于3.5%，PSO-BP 网络模型的相对误差均小于2.4%。BP 网络模型的相对误差变化幅度主要集中在[0,2.5%]，PSO-BP 的误差变化范围相对较稳定，主要集中在[－1.5%,1.5%]。

图5 两种算法的相对误差结果对比图

表1 为两种不同的网络模型算法误差对比表，其中BP 网络模型的绝对误差和相对误差，相比于PSO-BP 网络模型的数值均偏大。由此可以得出，通过改良后的PSO-BP 网络模型对电池SOH预估的精准度更高，在储能商业化应用方面研究的价值更大。

表1 两种网络模型算法输出结果误差对比

4 动态贝叶斯网络法

4.1 估计方法

贝叶斯网络(bayesian networks，BN)是一种描述数据变量之间依赖关系的一种图形模式，是一种用来进行推理的模型。动态贝叶斯网络(dynamic bayesian networks,DBN)相比于BN 加了一个时间维度，使人们可以对动态系统建模。DBN 用途广泛，例如用于语音识别、数字取证、蛋白质测序、生物信息学等[31]。

电池的SOH与SOC两种状态都与内阻相关，不同SOH的SOC-OCV曲线也不一样。DBN 设计结构如图6 所示。

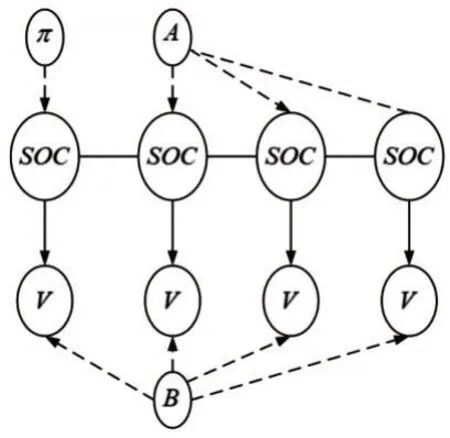
图6 DBN结构示意图

图6 中，SOC是DBN 模型的隐藏节点，不能直接观察到。电池的端电压作为DBN 的观测节点。p=(pi)表示初始状态概率的矢量，定义系统在初始时刻处于每个状态的概率[32]。A=(aij)是状态转移矩阵，它在时间t时对上一个状态转移矩阵给出的状态转移概率进行细化，即B=(bij)是混淆矩阵，包含隐藏状态SOC的观测电压的概率，即bij=P(Vt=Vi|SOCt=Sj)。SOC区间考虑的是恒流充电的范围，SOC从0 到100%分成N个相同的部分[33]。如表2 所示，取n=30。

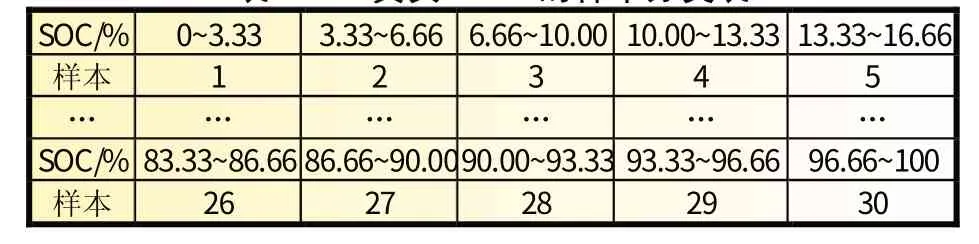
表2 真实SOC 的样本分类表

该模式下的电压也按同样方式分为M类，其中第j类的电压范围在Vmin+(Vmax－Vmin)×(j－1)/M和Vmin+(Vmax+Vmin)×j/M，Vmin和Vmax分别是充电过程中的最小、最大电压。在开始阶段，SOC可能是任意状态，故SOC的初始状态值认为是均匀分布的。可以得到：

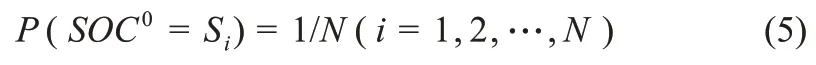
根据pi的定义有：pi=P(SOC0=Si)。矩阵A=(aij)和B=(bij)的大小分别为N×N和M×N，根据贝叶斯公式计算得到：

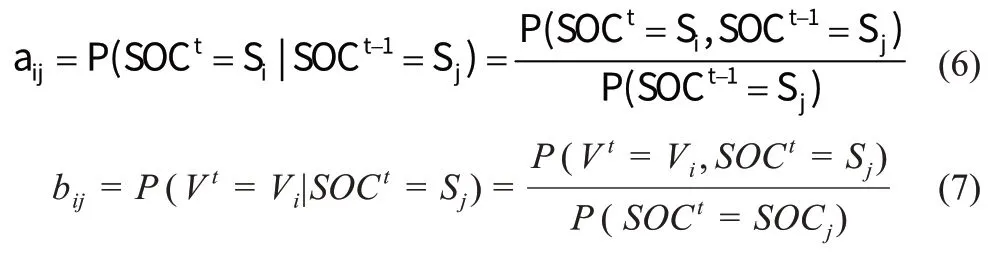
将得到的电池充电数据按老化状态分为K类。K值由Qcmax/Qn确定：如果Qcmax/Qn<80%，k=K，否则Qcmax/Qn≥80%，k=其中Qcmax为当前最大容量，Qn为电池标称容量。电池老化状态的分类如表3 所示。

表3 电池老化状态的5个分类

根据电池老化状态，定义了原精确SOH的模糊表示，然后再分别构建和训练K个不同的DBN 模型，以获得电池的预估SOH。

4.2 结果验证

在实验中，使用了21 个锂电池。对每个电池执行100 次生命周期测试，在充电过程中以10 s/次记录数据。为了获得不同老化条件下的数据，在电池的一些寿命周期实验之间，随机对电池进行老化加速过程，其中电池在55 ℃的高温下放电。然而，所有的充电过程都在25 ℃的恒定室温下进行。在21 个电池中，6 个用于模型验证。将其他15 组电池获得的1 500 组数据混合后分成两部分：随机抽取1 400 组进行模型训练，其余100 组进行模型验证。首先根据表3 将训练数据分为5 类，分别得到282、331、352、333 和102 组数据，然后用每一类数据训练5 个不同的DBN 模型。为了操作简便，从5 类中随机抽取一个数据进行作图，5 个DBN 的电压分布如图7所示。

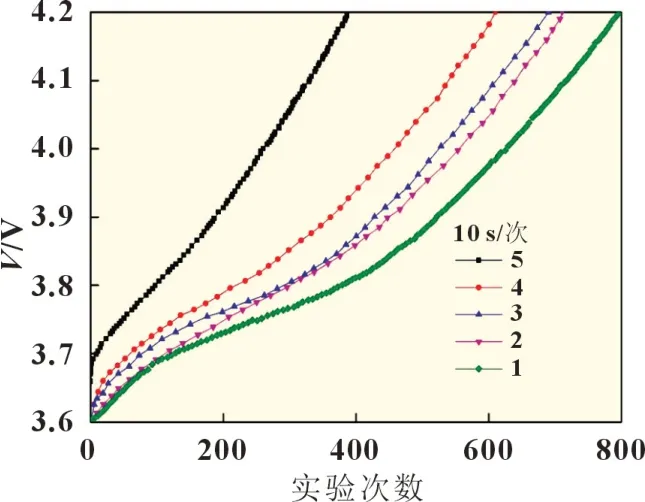
图7 使用5个DBN模型训练的电压分布

从所测试的电池全寿命周期数据结果来看，该测试得到的最大容量为5.086 Ah。根据SOH=Qcmax/Qn×100%可得被测电池的实际SOH为84.8%。

图8 为5 个不同的DBN 模型电压分布的归一化概率。从图中可以看出，相应的具有最大老化状态概率是第4 类。由表3 可知，其SOH对应为80%～85%。可以得到结论，该周期预测的模糊SOH与实际SOH一致。以归一化的概率作为权重，还可以得到预测的SOH，预测SOH为5 类加权预测的总和。对于该项研究，可以得到预测SOH：

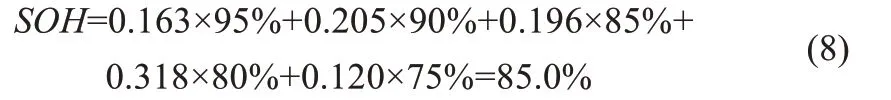
图8 根据5个DBN模型训练得到的归一化概率

可知，预测SOH与实际SOH非常接近，也足以证实该方法的精确率非常高。

5 结论

无论是电动汽车还是大规模储能应用场景，锂离子电池健康状态的参数都是非常重要的。最近在政策、技术的双重驱动下，我国储能站发展迅速，在电网侧、发电侧、用户侧及新能源配套等应用场景，建站数目越来越多，容量越来越大，但仍然缺少相关的标准。各电池厂家电芯容量不一、成组方式相异，BMS 厂家在运行方式、指标算法等方面也各不相同，造成储能站成本下降缓慢，投运后问题多，维护费用高等问题。

SOH是非常重要的一个参数，与电池内阻、电池老化状态、SOC等密切相关，是电池系统安全运行的指向。截至目前，不断爆出电动汽车自燃及储能站发生火灾。毫无疑问安全是人们追求的第一基本要素，因而如何更精准地预测锂电池SOH是至关重要的，具有较高的研究价值。

本文根据实际应用中发现的问题，综述了SOH的影响因素；根据最近关于研究SOH预测方法的最新成果，综述了三类典型方法。其中，线性预测误差方法应用广泛、预测结果较准，但是计算过程复杂；粒子群结合BP 神经网络法利用梯度降维方法，结构简单，参数单一，预测结果精准。但两种方法在单独使用时容易出现局部最优解问题，误差较大。动态贝叶斯网络法是基于SOC-OCV曲线建立的模型，计算形式以矩阵方式，数据量庞大，但是预测结果非常准确。总而言之，该文对锂电池健康状态运行、预估健康状态理论体系与实际发展研究具有一定的推动作用。尽管锂电池健康状态评估算法方面在实际应用上还稍有欠缺，相信在各类储能同行的共同努力下，在预估电池健康状态、寿命周期、降低成本等方面将取得长足进步，在保障储能站长期稳定运行上迎来更高峰顶。