基于天牛须搜索算法的电池模型参数辨识

曲云霄，林升垚，徐晋勇，莫 愁

(1.桂林电子科技大学机电工程学院，广西桂林 541004；2.桂林福达股份有限公司，广西桂林 541199)

为保证电池储能系统安全可靠地运行，需要电池管理系统(BMS)对锂离子电池的荷电状态(state of charge,SOC)、健康状态(state of health,SOH)、欧姆内阻等状态和参数做出估计和预测，而实现这些功能的前提是建立能够准确反应锂离子电池特性的电池模型。

锂离子电池的特性是非线性的，我们在外部只能监测端电压和负载电流，内部的SOC、SOH、内阻等参数都是无法直接测量的[1]。同时，负载工况和工作环境对其工作状态也有较大影响，如温度、放电倍率、放电深度等。因此，在对锂离子电池进行状态评估前，需先建立能够准确反应电池动态工作特性的模型。常用的锂离子电池模型主要有电化学模型和等效电路模型。

电化学模型精度高，然而涉及参数过多，计算量大而且复杂，无法应用于实时系统。

等效电路模型即以电容、电阻、电感等基本电气元件进行组合表达电池外特性的电池模型。将电池内部的复杂机理等效为较简单的电路模型，计算效率高，且易于理解。对比电化学模型，等效电路模型的参数大大减少，求解容易，因此该种类的模型目前被广泛应用于动力电池的实时管理。常用等效电路模型Rint 模型、PNGV 模型、RC 模型和Randles模型等。其中RC 模型较前两种模型电路通用性、可扩展性强，是目前用于锂离子电池状态评估的首选[2-4]。

RC 模型用理想电阻和电容并联组成组成RC 回路来模拟锂离子电池的极化特性，能够很好的模拟锂离子电池的外特性，但需要准确地标定模拟电路中理想电阻和理想电容的参数，然而此参数难以直接测量获得，需要进行估算辨识。理论上RC 模型的精度随着模型阶数的提高而提高，但研究发现，将模型阶数提高到二阶以上后模型精度的提高有限，且大大增加了计算量，因此本文选用二阶RC 等效电路模型进行电池建模。

最小二乘法是一种常用的模型参数辨识方法，可用于模型参数离线辨识，其递推形式可用于在线辨识。递推最小二乘法具有原理简单易于掌握，计算量小的优点，但锂离子电池模型的参数有时变特性，在电池持续运行的情况下，存在测量数据倍增同时伴随大量测量噪声的问题，此时以往常用的最小二乘法容易出现数据饱和，导致辨识出的模型偏差增大。林茂琼、陈增强提出递推阻尼最小二乘法，解决了数据饱和问题，但该算法用于模型参数辨识依然会导致较大的累计误差。陈坤息等提出采用偏差补偿最小二乘法用于模型参数辨识，对偏差进行修正补偿，提高了模型参数辨识精度。学界在对基于最小二乘法的模型参数辨识方法进行不断改进的同时，Scosati B、Chen kang 等引入粒子群优化(FSO)算法等智能算法开发出多种智能模型参数辨识方法，这类算法明显提高了模型参数在线辨识的精度，但该类算法往往存在容易陷入局部最优，以及计算量过大以致难以实现的问题。本文基于一种可以自动寻优的智能优化算法——天牛须算法，首次提出了基于天牛须搜索算法的电池模型参数辨识方法[5]。

1 变步长天牛须搜索算法

天牛须搜索算法(beetle antennae search-BAS)是一种智能优化算法，该算法的基本思想来自于生物界的一种叫做天牛的昆虫，该昆虫头前长有两只长长的触角，在觅食的过程中，天牛靠两个触角来感知食物的气味，当左边的触角接收到的气味信息比右边更浓时，天牛就向左边运动，反之就向右边运动。仿照天牛的觅食行为，可以开发出高效率的智能寻优算法[6-8]。该算法的具体原理如下：

首先对天牛的触须觅食功能抽象化，进行简化的建模：(1)将天牛的头部简化为一圆柱体，其口器侧圆形底面中部为质心，左右两须在两侧且距离质心距离相等；(2)天牛的每次移动的步长step与两须间距d0的比值为常数c，即step=d0×c；(3)天牛在移动到下一个位置后，随机改变头的朝向亦即随机改变触须的朝向。

在n维空间坐标系中，设质心坐标为X，左须坐标为XL，右须坐标为XR，左右两须间距为d0，天牛的头部朝向是随机的，从天牛的右须指向左须的向量也是随机的，设这个随机向量为dir=rands(n,1)，以此我们可以将左右触须的坐标用质心坐标进行标识：将左右两触须的坐标代入待寻优的函数f(x)，分别求值得到f(XL)，f(XR)。对两点的值进行比较，如果左须点对应的函数值更优，则天牛向左须方向移动一个步长step，反之则向右须方向移动一个步长。以寻找函数最小值为例：

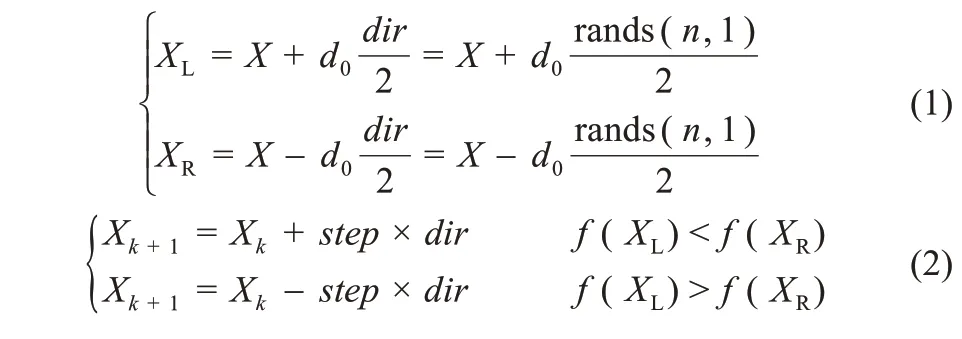
BAS 算法可以自动寻优，迭代次数无限时，其最终的收敛精度取决于步长。步长大则收敛快精度低，步长小则收敛慢精度高。针对提出的电池模型参数辨识工作，本文对该算法进行优化：先用大天牛(取d0较大值)进行工作，执行一定的步数后，减小d0的值，即减小两须间距，减小天牛头部大小，用小天牛继续求解，继续减小误差范围，如误差范围不能满足要求，则继续减小天牛大小，直到误差满足要求为止。经改进后的算法中的关键初始设置参数有：初始位置X0，初始步长step，单步长最大步数kmax，步长缩小率η。初始位置的选取应尽量靠近最终结果，应按经验或已有数据进行取值。由于步长与触须距离相关，为简化算法，本文将c选为1，即步长与触须距离相同，初始步长的选取应尽量大，本文选取的是与自变量的最大长度相同。单步长最大步数的取值应在满足取值精度的前提下尽量小，以减少计算量[9]。步长缩小率的取值在(0.1)区间内，缩小率η越大，收敛速度越慢，但若η过小，可能会导致不能收敛到真值。根据实践应用经验，取值范围在(0.8,0.95)为宜。

具体步骤如下：(1)设置初始位置X0，初始步长d0；(2)生成指向随机的n维单位向量，根据生成的向量生成左右须XL，XR；(3)计算左右两须的函数值，选择最优的作为此次迭代的新位置Xi；(4)判断Xi处的函数值F(Xi)是否满足要求，如满足要求，到步骤(6)，如不满足，回到步骤(1)再次迭代；(5)检查步数i是否达到最大步数，如达到最大步数，缩小步长；(6)输出最优结果Xi的值。

2 磷酸铁锂电池建模

将理想电容电阻元件进行并联组成RC 回路，再将RC 回路与理想电源、欧姆内阻进行串联即可得到RC 等效电路模型，RC 回路的数量即为RC 等效电路模型的阶数。理论上模型阶数越大，模型精度越高，但大量的研究证明，将模型的阶数提高到三阶以及三阶以上时，随着阶数的提高，模型精度提高极小，且所需计算量剧增。因此，在平衡了计算量与模型精度后，本文采用了二阶RC 等效电路模型为例进行分析，其原理如图1 所示。图中：Uoc为电池开路电压，UL为锂电池负载端电压，R0为欧姆电阻，RC1、RC2和CC1、CC2分别表示极化电阻和极化电容。

图1 二阶RC等效电路模型原理图

搭建等效电路模型后，要完成电池模型的搭建，还需要知道OCV与SOC的函数关系式。OCV与SOC是呈正相关的。通常，我们认为：当OCV为放电截止电压时即为电池电量耗尽，此时SOC为0；当OCV为电池最大电压时即为电池满电，此时SOC为1。该关系由实验测得，经电池充放电实验后得到的数据组成因锂离子电池的OCV-SOC曲线在10%～90%时存在“平台区”，过渡平缓，而在10%以下和90%以上斜率较大。为描述OCV-SOC曲线中电压在0 和1 附近处的剧烈变化情况，本文采取一种可变参数的双指数模型。

根据二阶RC 等效电路模型和双指数OCV-SOC曲线进行电池建模的步骤如下：

设OCV为Uoc，根据图1 所示的电路模型，其数学模型可以表示为：

根据基尔霍夫定律：

设SOC为Z，电池0%容量时的电压为U0，电池的库仑效率为η，电池的总容量为Q，有：

式中：α1、α2、β1、β2、γ为可变参数，α1、α2、β1、β2分别模拟了电压在SOC为0 和100%附近的剧烈上升下降，γ用来模拟“平台区”的线性特性。该OCV-SOC曲线只有5 个可变参数值，需要的计算量较小。该方法的建模数据是等温数据，最终得到的曲线是等温情况下的曲线，要得到不同温度下的OCV-SOC曲线，要在不同温度下进行测试标定可变参数值，对于两组温度之间的情况，可以对可变参数进行插值估计。

将式(3)、(4)、(5)整理后，得到式(6)：

采用双线性变化法将模型映射到Z平面，再进行逆Z变换：

设Δt为采样间隔，u=I，C=-[1,1,0]，D=-RC0，y=UL。

根据离散化公式：

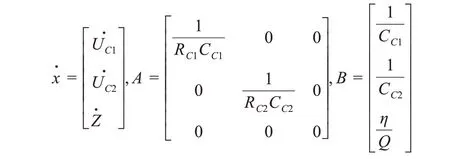
得到离散化的等效电路模型状态方程：

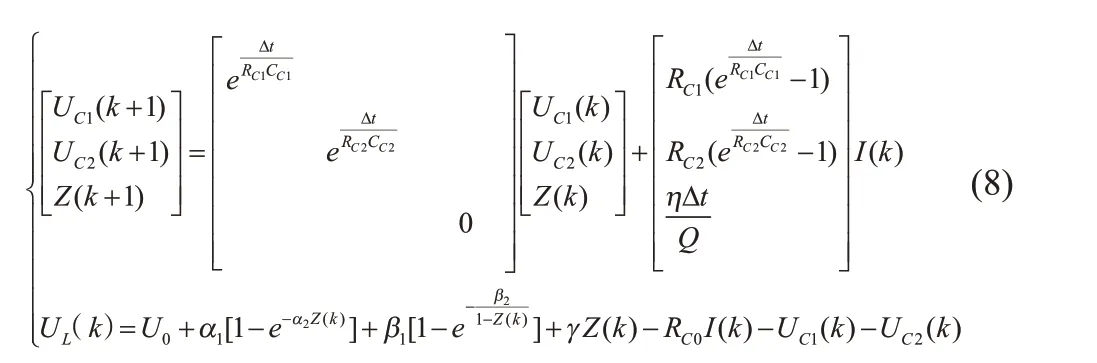
3 模型参数辨识

本文基于变步长天牛须搜索算法的系统辨识获取二阶RC 等效电路模型中参数，将电池视为动态系统，分别对OCVSOC曲线以及RC 参数进行辨识。

OCV-SOC曲线中需要辨识的五个参数为α1，α2，β1，β2，γ，设BAS 算法中的天牛质心坐标为X(α1，α2，β1，β2，γ)，由于实验测量得到的OCV-SOC数据是离散的，设数据的序数为i，SOC为0 时i=1。对应的SOC值为Zi，开路电压值为Ui。本文采用均方差作为适应度函数。

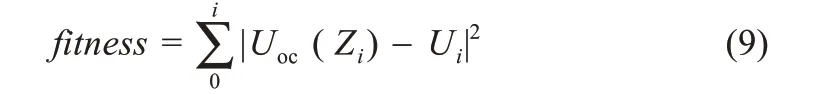
式中：Uoc为电压测量值；Ui为拟合值，辨识结果为：α1=-0.573，α2=19.20，β1=-0.102 2，β2=1.014 6，γ=3.355。

对拟合出的曲线与测量值对比进行误差分析，可以得出：最大绝对误差为0.265 V，最大相对误差为0.97%，绝大多数测量点位的拟合相对误差小于0.4%。

从图2 分析可以看出，BAS 算法辨识的双指数OCV-SOC拟合曲线整体精度较高、拟合效果较好，仅在SOC接近0 或1时由于OCV值变化剧烈导致误差较大，但仍然可以保证最大绝对误差不超过0.03 V，最大相对误差不超过0.97%。之后再对RC0，RC1CC1，RC2CC2进行拟合辨识，得到辨识结果如表1所示。

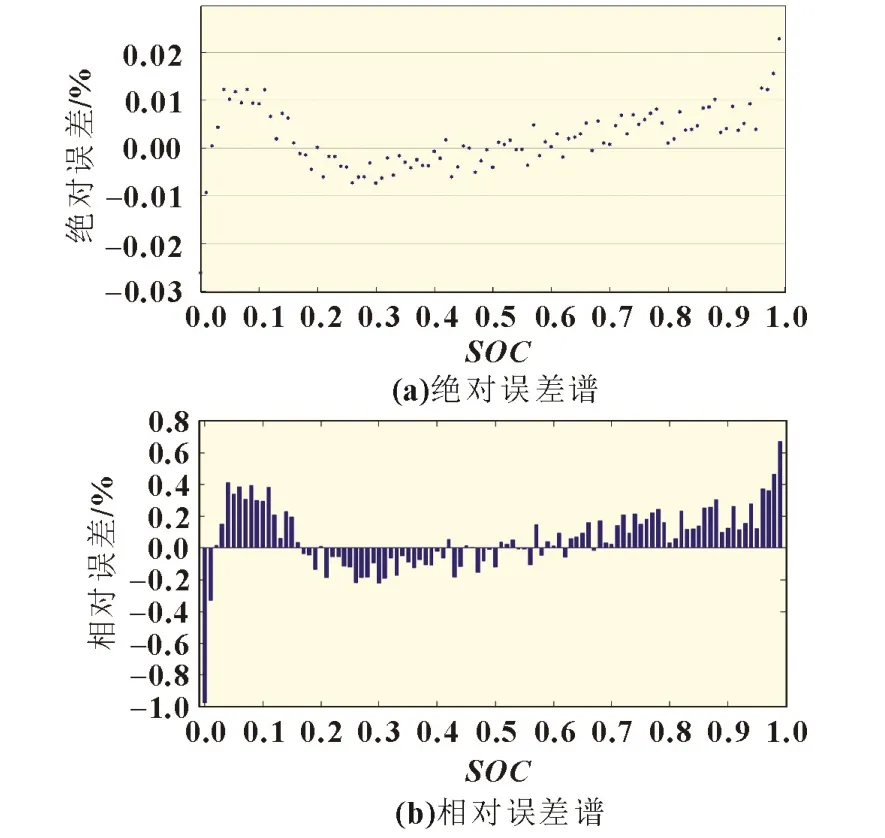
图2 OCV-SOC曲线辨识结果

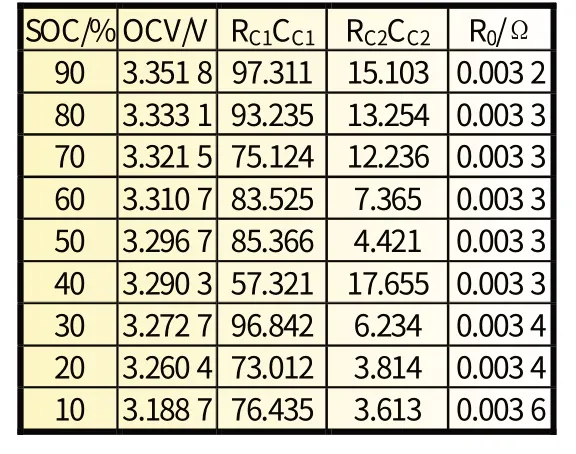
表1 模型参数辨识结果

4 仿真实验验证

为验证双指数拟合的OCV-SOC曲线的建模性能以及BAS 算法辨识的模型参数的有效性，在MATLAB/Simulink 中搭建模型进行仿真验证。将BAS 算法辨识出的模型RC 参数以及OCV-SOC曲线代入Simulink 模型中，SOC计算方法采用理想状态下的安时积分法。搭建的仿真模型如图3～6 所示。

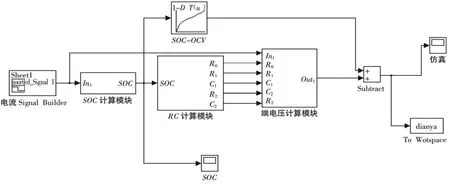
图3 Simulink电池仿真模型

图4 SOC计算模块

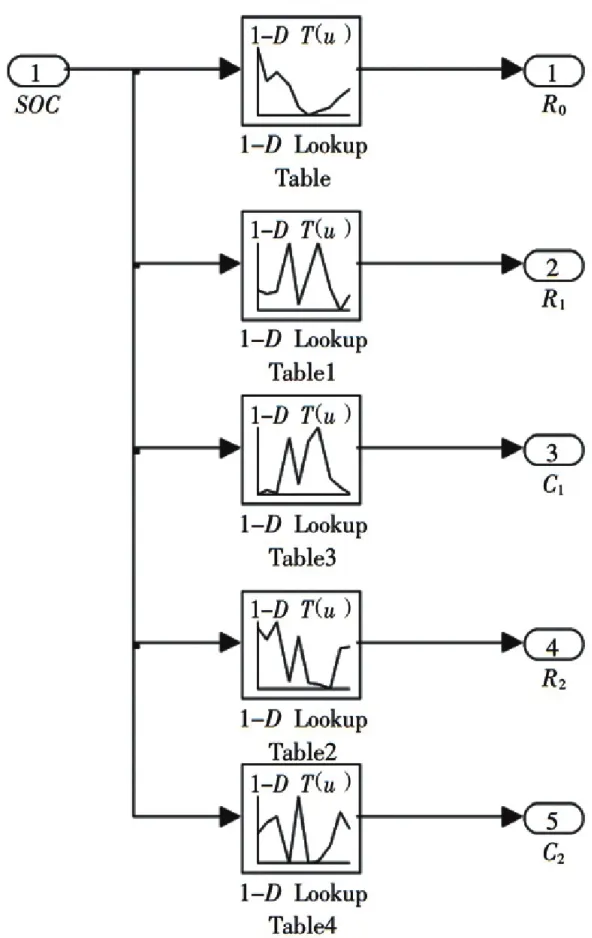
图5 RC计算模块

图6 端电压计算模块

对模型进行脉冲放电测试，放电倍率为2C，设定初始SOC为0.9，进行放电50 s，然后静置50 s 进行仿真验证，截取其中两段如图7 所示。

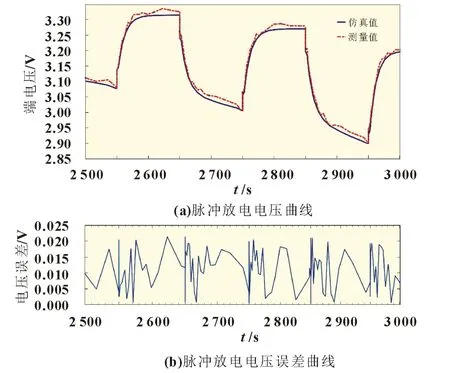
图7 脉冲放电仿真结果

从图7 分析可以看出，BAS 算法所辨识出的模型，在脉冲放电的情况下，电池模型的输出电压与测量电压值很接近，最大电压误差不超过0.023 V。

模型进行恒流放电测试，放电倍率为1C，设定初始SOC为0.9，将测试电流输入模型中得到的仿真结果如图8 所示。

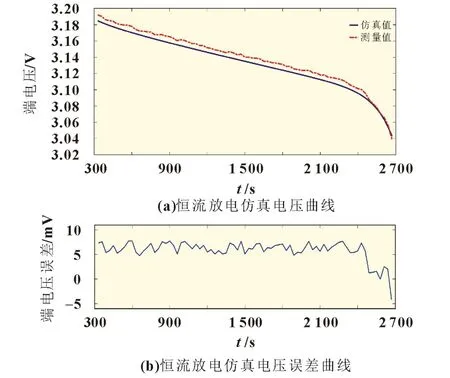
图8 恒流放电仿真结果

从图8 可以看出，BAS 算法所辨识出的模型，在恒流放电的情况下，在放电的中段，误差很小且稳定，在0.005～0.01 V之间波动，在放电末端由于电压快速下降，误差出现波动，但仍在比较低的范围内。

对本文搭建电池模型，使用BCRLS(带偏差补偿的最小二乘法)和RLS(最小二乘法)进行重新辨识，进行脉冲放电仿真实验，与本文提出的基于BAS 算法的模型参数辨识方法结果进行比较，由于在低电量时误差较大，因此本文取SOC值在20%～80%之间时的仿真结果进行采样比较。结果如图9所示。

图9 三种算法辨识误差比较

从图9 分析可以看出，由于原理基本与RLS 算法相同，BCRLS 算法与RLS 算法有误差波动现象，且波动趋势基本一致。BCRLS 算法引入了偏差修正，其总体误差较RLS 算法较小。BAS 算法的辨识误差远远低于BCRLS 和RLS，且在电池SOC值中段放电时没有与以上两种算法类似的有规律的波动。

5 结语

本文基于二阶RC 等效电路模型和双指数拟合函数，建立了参数可辨识的锂离子电池模型，针对此模型提出了基于BAS 算法的模型参数辨识方法，并对辨识的模型进行了仿真测试，仿真结果表明：

(1)本文提出的基于BAS 算法的模型参数辨识方法相比传统的最小二乘法及其改进算法有更高的辨识精度。

(2)电池充放电的初始阶段和放电末端由于电压波动大，双指数函数的拟合误差较大，导致辨识的模型误差在首尾两端较大。

(3)模型在SOC值0.2～0.8 的中段充放电范围内，最大动态误差不超过0.025 V，最大静态误差0.01 V，具有较高的精度，说明本文的模型以及辨识方法能够准确模拟磷酸铁锂电池中段的“平台区”特性。