基于iSIGHT 的深海载人平台总装台架重量优化

刘一夫，渠继东，邢 福

(1.中国船舶科学研究中心，江苏 无锡 214082；2.深海载人装备国家重点实验室，江苏 无锡 214082)

0 引 言

深海载人平台的总装台架作为框架结构的基础，承担平台总装过程中的结构载荷、设备载荷、人员载荷以及施工吊装等带来的其他载荷[1]。由于总装台架尺寸较大，重量较重，对其进行重量优化可以节约加工运输成本。本文以某深海载人平台总装台架为例，对其进行结构屈服强度校核。以重量为目标通过iSIGHT优化设计平台建立单目标优化模型，采用单目标优化中的自适应模拟退火算法（ASA）并以屈服强度作为约束，最终得出优化方案。

1 总装台架屈服强度计算

总装台架由上下两部分组成。上层为3 组尺寸相同的带有肋板的支撑结构，下层为由方管连接而成的“日”字型结构。上下2 层通过焊接固定。模型采用板单元建立，单元尺寸0.2 m×0.2 m，如图1 所示。

图1 有限元模型Fig.1 Finite element model

模型材料选用Q235-A 钢，屈服强度 σs=235 MPa，弹性模量E=2.06×105MPa，泊松比 μ=0.3，密度ρ=7.8×103kg/m3。参照深海载人平台设计结果，模型总质量约为106 t。根据《潜水系统与潜水器入级与建造规范》中的规定，考虑动载情况下的安全系数取2.0。因此模型所受载荷为2 080.8 kN。根据实际承载情况台架受力区域分为6 块，每一块受力区域尺寸相同，为4.4 m×0.8 m，受力节点数为120 个。由此可得模型总受力节点数为720 个，每一个受力节点施加2 890 N 的节点集中力。台架模型载荷施加情况如图2 所示。台架在实际总装过程中，需要对四角进行固定，防止其平移或转动。参照实际情况，对台架模型四角进行约束，位移与转角均为0。台架模型约束情况如图3 所示。

图2 模型载荷施加Fig.2 Model load application

图3 模型约束定义Fig.3 Model constraint definition

台架模型按照分组设置板厚，共分为4 组。底部由方管组成的框架为一组，板厚10 mm，上层支撑结构的面板和腹板为一组，板厚20 mm，上层支撑结构肋板为一组，板厚10 mm，上层支撑结构和下层框架重叠部分为一组，板厚是二者的和，为30 mm。台架模型板厚分组设置情况如图4 所示。

图4 模型板厚设置Fig.4 Model plate thickness setting

根据《潜水系统与潜水器入级与建造规范》中附录B 的规定，结构相对与安全系数的许用应力值 [σ]可以表示为：

其中：ReH为材料的屈服强度，N/mm2。总装台架处于放置状态，因此安全系数取1.15，结构相对于安全系数的许用应力值为204 N/mm2。经过有限元计算，该工况下台架模型最大屈服应力为137.14 MPa，结构重量为61.2 t。计算应力云图如图5 所示。

图5 计算结果应力云图Fig.5 Stress nephogram of calculated results

根据云图可知，最大应力发生在底部框架方管连接处，为137.14 MPa，其余部位应力值较小，相对于许用值而言仍有较大的强度裕度。考虑到此时结构重量较大，势必增加加工运输上的难度，同时也增加了建造预算，因此需要对台架结构进行满足屈服强度前提下的重量优化。

2 重量优化

基于iSIGHT 优化平台，对目标台架结构进行以重量为目标的单目标优化。单目标优化算法大体上分为3 类：梯度优化法（Gradient Techniques）、直接搜索法（DirectMethodsTechniques）、全局搜索法（Exploratory Techniques）。梯度法能在设计点周围进行快速的搜索，直接搜索法也能在设计点周围进行快速的搜索，并且搜索阶段采用大步长，具备比梯度优化法更大的搜索空间。然而以上2 种方法容易受设计点初始位置影响，陷入局部最小解，无法对全局进行搜索。全局搜索法在全局整个空间内搜索最优解，不依赖于设计点初始位置，避免了陷入局部最优解的情况[2]。

2.1 优化算法选择

优化算法的选择对最终优化结果具有决定性的影响[3]。根据刘峰的研究结果[4]，对单目标优化算法的比较结果，全局搜索法中的自适应模拟退火算法（ASA）优化效果最好。因此本文采用全局搜索法中的自适应模拟退火算法（ASA）进行单目标优化。自适应模拟退火算法（ASA）是20 世纪90 年代初期，Lester Ingber 根据传统模拟退火算法和模拟淬火过程提出的一种算法，该算法非常适用于算法简单的高度非线性优化问题，能够辨识不同位置的局部最优结果，具备以最小成本得到最优解的能力[5-8]。该方法通过模拟退火的过程，将优化问题与统计力学中的热平衡问题进行类比，对初始点开始进行的每一步都进行计算比较，计算得到的函数值只要下降即被接受，反复计算最终得到最优点[9]。此外，函数值的上升也有可能被接收，这样可以避免陷入局部最优解，这正是该算法相比梯度优化法的优势所在。函数值上升的点是否被接受，要依据温度函数Metropolis 判据[10]。在温度函数不断降低过程中，考虑概率突跳特性在解空间中搜索目标函数的全局最优解，即能在局部最优解跳出并最终趋向全局最优解。

2.2 iSIGHT 优化框架建立

iSIGHT 优化平台可以通过MSC.Patran 模块或者Simcode 组件进行集成优化[11]。Simcode 组件具有不受MSC.Patran 版本限制，操作更加清晰的特点，因此这里采用Simcode 组件进行集成优化。Simcode 组件的输入为已经录制好的.ses 文件作为模板，命令为自行编制的.bat 批处理文件。通过解析.ses 文件中的板厚属性，将总装平台4 组板厚分别定义为设计变量，分别为底部框架板厚t1，面板腹板板厚t2，肋板板厚t3，重叠部位板厚t4。考虑到实际加工建造过程中，重叠部位板厚可以独立于底部框架板厚和面板腹板板厚，因此在优化时将其作为一个独立的设计变量。.bat 批处理文件在MSC.Patran 中运行已经录制好的.ses 文件，实现对修改板厚—屈服强度计算—结果输出的全过程。输出结果为.rpt 文件和.f06 文件。通过解析输出的.rpt 文件和.f06 文件中总装台架的重量和最大应力，并分别作为目标函数和约束值，最终完成优化框架的搭建。优化模型设置如下：

变量增量为0.1 mm。

需要注意的是，在搭建优化框架时，要检查输入输出文件的路径。例如.ses 文件中，对.op2 文件的输出与读取、.rpt 文件的输出等，为了更灵活搭建优化框架，应尽量避免绝对路径的出现，以免造成优化结果不变的情况。

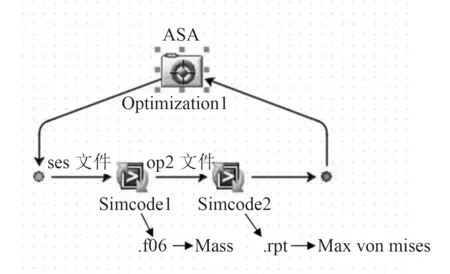
图6 优化框架示意Fig.6 Schematic diagram of optimization framework

3 优化结果及分析

经过200 次迭代优化完毕，最优解点为第179 次迭代结果。根据计算过程监控可知优化过程中设计变量、目标函数Mass,Max von Mises 的变化过程以及设计可行性（Design feasibility）。相关参数随迭代变化过程如图8 所示。

图7 底部框架板厚t1 随迭代次数变化Fig.7 Variation of t1 with number of iterations

图8 面板腹板板厚t2 随迭代次数变化Fig.8 Variation of t2 with number of iterations

由计算可知优化结果为底部框架板厚t1=8.1 mm,面板腹板板厚t2=10.5 mm,肋板板厚t3=5.3 mm,重叠部位板厚t4=5.5 mm，对应总装台架重量为36.713 89 t，最大应力为197.661 346 MPa，小于许用值满足设计要求。与原有方案相比，优化方案减重40.01%。

图9 肋板板厚t3 随迭代次数变化Fig.9 Variation of t3 with number of iterations

图10 重叠部分板厚t4 随迭代次数变化Fig.10 Variation of t4 with number of iterations

图11 重量及最大应力随迭代次数变化Fig.11 Variation of weight and maximum stress with number of iterations

图12 设计可行性随迭代次数变化Fig.12 Variation of design feasibility with number of iterations

表1 优化方案与初始方案板厚比较结果Tab.1 Plate thickness comparison between the optimized scheme and the initial scheme

提取优化方案与初始方案中，4 组板厚对应的板单元最大应力，对应结果如表2 所示。

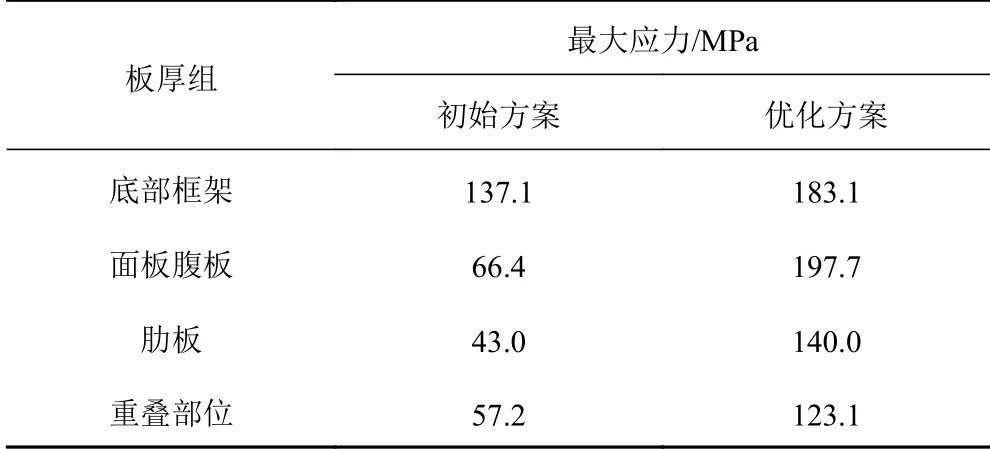
表2 优化方案与初始方案应力结果比较Tab.2 Comparison of stress results between the optimization scheme and the initial scheme

以优化方案中底部框架结构为例，其应力云图如图13 所示。可知，最大应力仍然发生在方管连接位置，为183.1 MPa，接近许用值。方管中段部分应力范围在100 MPa 以内，距离许用值仍有一段距离。因此如果将方管分为若干段，并赋予不同板厚，可以将重量进一步优化。同理，肋板、面板腹板、重叠部位板厚也可以细化成若干组。也就是说，本例中优化模型中的设计变量适当增加，可以得到重量更小的优化方案，这有待于下一步研究工作进行。

图13 优化方案底部框架应力云图Fig.13 Stress nephogram of bottom frame in optimization scheme

根据优化方案最大应力可知，优化方案是满足屈服强度前提下重量最优的方案。然而在许多其他结构设计中，结构的稳定性等同样应当作为约束条件。例如深海载人平台的框架、耐压壳体等结构，在优化时需要定义多个约束条件才能保证优化方案的可行性，此时可以采用NSGA-Ⅱ 优化算法对模型进行多目标优化，优化思路和具体过程与上述重量优化相似。因此在深海载人平台其他结构设计中，要根据结构的具体情况具体分析，最终形成可靠的优化方案。

4 结 语

本文基于iSIGHT 优化软件对某深海载人平台总装台架进行结构屈服强度校核和重量优化，得出如下结论：

1）该总装平台在设计载荷下满足结构屈服强度要求，存在较大的强度裕度；

2）采用自适应模拟退火算法（ASA）对目标台架进行重量优化，得到优化方案较初始方案减重40.1%，达到重量优化的目的。

针对总装台架的重量优化方法对深海载人平台结构设计具有一定参考价值。对于其他结构的优化设计思路与方法大同小异，需要注意的是要根据实际情况确定约束种类与个数，从而选择优化算法进行单目标/多目标优化，最终形成可靠的优化方案。