基于网格化应力场的边坡滑移面搜索模型及应用
李 忠, 张 曦, 汪红星
(1. 上海工程技术大学 城市轨道交通学院, 上海 201620; 2. 兰州理工大学 土木工程学院, 甘肃 兰州 730050)
随着人口不断增多,国内外科技不断发展,人们对交通运输、旅游、住宅等方面的需求持续增加,使得自然边坡、人工边坡被大量使用.边坡在地震、降水的作用下或人为施工过程中极易发生崩塌、滑坡、泥石流等自然灾害.因此,边坡灾害防治问题越来越受到人们的关注,边坡稳定性分析变得尤为重要.正是因为大量学者持续地重视,边坡稳定性研究工作得到了不断地发展.
边坡稳定性分析通常以极限平衡法和有限元法为主.极限平衡法是将边坡稳定问题当作刚体平衡问题来研究,即将组成滑坡体的岩土体视为在复杂状态下的刚体.许多学者假定了岩土块之间接触面上作用力的方向,分布情况及作用位置等,进而衍生出了多种不同类型的极限平衡法[1].如Fellenius提出的瑞典条分法、Bishop法.之后,Janbu等[2]基于Bishop安全系数的定义又对条块受力模式及滑面形状进行过不同假设,提出了其他极限平衡方法.近年来,周豪等[3]提出了基于滑面正应力修正的极限平衡法.王旭等[4]考虑土体多种条件参数的随机性与变异性,在极限平衡法分析边坡稳定性时加入了可靠度理论.除此以外,陈祖煜等[5]提出了一种将二维Spencer法扩展到三维的边坡稳定性分析方法,该法在保证了滑坡体三个方向满足静力平衡的同时,还增加了一个整体力矩平衡条件,不再将行界面的条间力假定为水平,也不再将条底的剪力方向假定为平行于主滑平面方向.符贵军等[6]发现现有的Sarma在进行边坡分析时未考虑水平地震作用力的角度,进而提出一种考虑水平地震加速度方位角的改进Sarma法.邓东平等[7]通过对一般情况下的条柱进行受力分析,从而建立了一种能同时满足3个力和3个力矩平衡方程的准严格三维极限平衡计算公式.但由于这些方法都有着众多的假定,尤其是假设了滑移面的形状,极大限制了极限平衡法的应用范围.近年来随着计算机的发展,国内外在进行边坡稳定性分析时逐渐开始使用限元法与计算机相结合的方法,能更好地对滑移面进行确定,进而对边坡稳定性有了更加准确地分析.一些学者已经做出了一些研究,如在用有限元分析建立应力场的基础上,采用蚂蚁算法搜索出更接近实际情况的滑移面从而对边坡稳定性进行分析[8],但这种算法有着收敛慢、容易陷入局部最优的缺点.除此以外,在已知应力场的情况下,使用多种群遗传算法构建适应度函数搜索最危险滑移面,达到边坡稳定性分析的目的[9];在二维的基础上又提出了相应的基于MPGA的三维边坡稳定性分析方法[10];在边坡稳定性分析中应用一种简单的遗传算法搜索临界非圆弧破坏面,并用Mangnestern-Malk方法求解安全系数,分析了自然斜坡上既有建筑物和建筑物对地震和附加荷载的影响[11].但遗传算法有着编程过程较为复杂、交叉率和变异率等参数通常需要靠经验选择的缺点.
基于以上分析,使用有限元建立应力场,再结合计算机编程语言对应力场进行分析,建立一种基于网格化应力场的边坡滑移面搜索模型能有效避免其他算法存在的不足.该方法不再局限于极限平衡法的种种假设限制,尤其是滑移面的假设,能适用于任意应力状态(极限状态或非极限状态)下边坡稳定性分析,更加接近边坡的真实受力情况.
1 边坡稳定性分析模型
1.1 建立模型
将数值应力场与MATLAB编程相结合,在MATLAB软件中利用坐标在平面内将边坡重新划分一种单元大小均等的新网格,从而建立一种边坡稳定性分析通用模型.通过编程对数值应力场进行分析,得到边坡最小安全系数,从而达到边坡稳定性分析的目的.这种模型的关键在于,利用新网格通过搜索条件为安全系数的计算提供滑移面.应力场与程序两者相辅相成,紧密结合,最终得到最危险滑移面及其所对应的最小安全系数,并进行边坡稳定性分析.
1.2 模型实现关键步骤
1) 根据土层参数使用MIDAS-GTS有限元分析软件建立边坡二维模型,导出模型相关的节点及单元坐标等信息.采用非线性静力分析计算边坡,计算后通过对结果进行后处理可以得到边坡的数值应力场情况.
2) 将保存的模型节点单元及计算得到的数值应力场相关数据信息以数值矩阵形式导入MATLAB.在MATLAB中使用编程语言重新建立二维直角坐标系,通过坐标信息将模型重新划分为新的网格式模型.
3) 建立原单元与新划分网格模型单元的应力对应关系,将新的网格单元以每一竖条分为一组.利用土体单元评判准则在每一竖条里找到最危险的单元(最可能达到屈服条件的单元)进行标记,最终找到并绘制所有最危险单元组成的边坡最危险滑移面,也就是最小安全系数所在的滑移面.
4) 根据最危险滑移面上所有单元的应力情况,采用矢量和法计算边坡最危险滑移面所对应的安全系数,从而达到对二维边坡进行最危险滑移面搜索及计算安全系数进行稳定性评价的目的,从而对边坡进行稳定性分析.
1.3 模型实现关键问题
1.3.1新网格的划分
根据有限元计算模型的尺寸大小重新建立二维直角坐标系,将边坡宽度和高度所围成的矩形范围划分为大小相等的新单元网格,如图1所示.在x-y坐标内,沿x方向将模型划分为a个网格,使得模型被划分为a个竖条,再将每一竖条沿y方向划分为b个网格,从而形成新的网格模型.为了使得计算结果相对准确,新划分的网格单元尺寸应略大于有限元计算时的网格,尽量保证每一个新单元内存在一个完整的原有限元单元.
1.3.2单元内离散点应力计算
1) 确定新单元与原有限元单元的应力关系
如图2所示,取原有限元模型单元四个角点坐标的最大最小值,即单元的大小范围,如图2中矩形ABCD所示,得到搜索矩阵
A=[xmin,xmax,ymin,ymax]
找到新网格式模型单元如图2中虚线框所示中心点i的坐标同时满足以下条件的所有单元:
xmin 再根据SABCD=SA+SB+SC+SD找到满足条件的唯一对应的单元. 2) 计算滑面上点i的主应力 在四边形ABCD内任意点i的主应力可由四个角点的应力通过形函数按比例等参差值的方法计算得到,可由下式表达: (1) 上式中形函数Ln如下: (2) 1.3.3土体单元判别准则及构建判别函数 边坡发生破坏时会在坡体内形成一条相对软弱的带,称之为滑移面.坡体沿滑移面土体发生剪切破坏,从而使边坡发生失稳.滑移面是由无数发生破坏的土体单元组成的,所以可通过搜索出最有可能发生破坏的土体单元,从而进一步确定边坡的最危险滑移面.通常采用摩尔-库伦准则评判土体单元破坏问题[12],即土体沿某一平面的剪切应力与黏聚力的差值和正应力的比值达到土体内摩擦角的正切值时,表示土体单元在这个平面处于临界破坏状态,具体情况见下式: (3) 在式(3)的基础上构建判别函数f如下式所示: (4) 以该式作为靶单元的搜索标准,计算每一竖条所有单元的f值,则有:当f<1时土体单元未发生破坏;当f≥1时土体单元发生破坏.考虑到同一竖条中可能存在多个单元发生破坏,此时取f值最大的单元为该竖条最易发生破坏的单元(最可能发生屈服单元)进行标记,进而找到所有竖条的最危险单元所组成的边坡最危险滑移面. 1.3.4安全系数的计算 在平面问题中,平面内任意一点的应力状态,可用3个主应力σ1、σ2、σ3来表示[12].故而边坡滑移面上任一点的正应力和切应力可用下式计算: (5) 式中:σi、τi为滑面上i点处的正应力和切应力;φ表示土体内摩擦角. 矢量和法指边坡在外部荷载的作用下,潜在滑移面上的极限抗滑力的总和与滑动力的总和之比[13].矢量和法由葛修润院士提出,现在被越来越多的学者应用于二维以及三维边坡的稳定性分析中,其中二维的矢量和法安全系数计算模型如图3所示,安全系数由式(6)可得[14]: 图3 矢量和法安全系数计算模型Fig.3 Vector sum method safety factor model τfi=c+σitanφ (6) 式中:τfi为i点的抗剪强度,其抗剪强度符合摩尔-库伦定律,可由式(7)表示[15]: (7) 式中:Δli表示滑面上i微段的长度;αi表示i微段与水平方向的夹角;n表示滑面的微段总数;θ表示投影方向与水平方向的夹角,可由式(8)表示: (8) 由于单元划分较密,所以滑移面上两点之间连线可以近似的看作一条直线.计算安全系数时,如图2所示,可以分别求得滑移面上i点与相邻两点i+1和i-1的中点ii和ii-1的坐标,在ii和ii-1所连成的直线上求得i点的应力积分,根据式(6~8)可以求得边坡的安全系数. 以澳大利亚计算机协会(ACADS)所提供的考试题目为例[16].该边坡为一个均质边坡,坡比为1∶2.该算例通常被国内外学者们用来检验二维边坡计算模型的可行性.算例边坡的尺寸、边界条件等具体情况如图4所示.土层参数:黏聚力c=3.0 kPa,内摩擦角φ=19.6°,弹性模量E=10 MPa,容重γ=20 kN/m3,泊松比μ=0.3. 利用MADIS-GTS建立的有限元计算模型如图4所示,宽度方向为40 m,高度方向为20 m.该二维模型荷载只考虑自重,其边界约束条件为,上边界自由无约束条件,左右边界进行水平约束,下边界进行水平及竖向约束.采用非线性静力分析,计算得到边坡的应力场情况.该模型共划分3 400个单元,3 526个节点. 图4 边坡有限元计算模型 (m) 将该算例用极限平衡法计算得到最危险滑移面及最小安全系数,再将其结果与本文基于应力场的网格式计算模型对该算例进行稳定性分析所得的结果进行对比.对滑移面与安全系数分别进行比较.滑移面形状及位置具体情况如图5所示,两种方法所得边坡安全系数对比结果见表1. 图5 滑移面示意图Fig.5 Schematic diagram of slip surface 表1 安全系数对比结果 图中分别绘出极限平衡法及本文方法所计算的结果以及边坡的坡线,从图5所示滑移面可知,基于应力场的滑移面搜索模型所搜索到的滑移面和极限平衡法相比,前者得到的滑移面曲线始终在极限平衡法所得的滑移面曲线附近波动,表明了基于应力场的网格式边坡滑移面搜索模型进行滑移面搜索及边坡稳定性分析的可行性. 从表1可以看出基于应力场的滑移面搜索方法计算出的安全系数和极限平衡法给出的答案相差不大.其中极限平衡法所计算的结果较小,这是由于极限平衡法的种种假设限制导致其结果较为保守,进一步说明了基于应力场的网格式滑移面搜索模型进行滑移面搜索的合理性. 1) 网格化应力场边坡滑移面搜索模型无需对滑移面的形状与位置等进行假定,通过单元土体应力分析的方式,在平面内搜索出潜在破坏土体单元,构建二维滑移面,为二维边坡潜在最危险滑移面的自动搜索创造条件.该方法的优点在于能适用于任意应力状态(极限状态或非极限状态)下边坡稳定性分析,使得该方法能应用于主动加固条件下边坡稳定状态评价. 2) 通过对ACADS经典算例的计算和分析,将两种方法计算结果进行对比分析,验证了该种方法可以适用于边坡稳定性分析,滑移面形式为不规则曲线,更符合边坡的真实受力状态. 3) 如何将基于应力场的二维边坡滑移面搜索及边坡稳定性分析方法应用于复杂应力状态下的边坡,及将该方法扩展到三维边坡的稳定性分析,后续还需进一步深入的研究.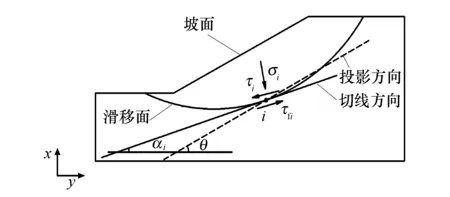
2 典型算例分析
2.1 算例介绍

2.2 结果对比分析


3 结论
——结构相互作用的影响分析

