一种基于OFDM-chirp的雷达通信一体化波形设计与处理方法

赵玉振 陈龙永 张福博 李焱磊 吴一戎

(中国科学院空天信息创新研究院 北京 100190)

(微波成像技术国家级重点实验室 北京 100190)

(中国科学院大学 北京 100049)

1 引言

雷达通信一体化是当下非常热门的研究领域，在抗震救灾、车辆组网、地形测绘等领域都非常有意义[1–4]。一种用于救灾的雷达通信一体化系统示意图如图1所示，飞机平台搭载可以用于探测成像的合成孔径雷达(Synthetic Aperture Radar,SAR)，在探索地形的同时与地面救援车辆保持通信，及时传输探测结果。如果雷达与通信系统各自分立，没有进行一体化设计实现良好的兼容性，不仅会增加飞行平台的载荷重量，还可能发生两种功能互相干扰的情形，导致系统的整体性能下降[5]。

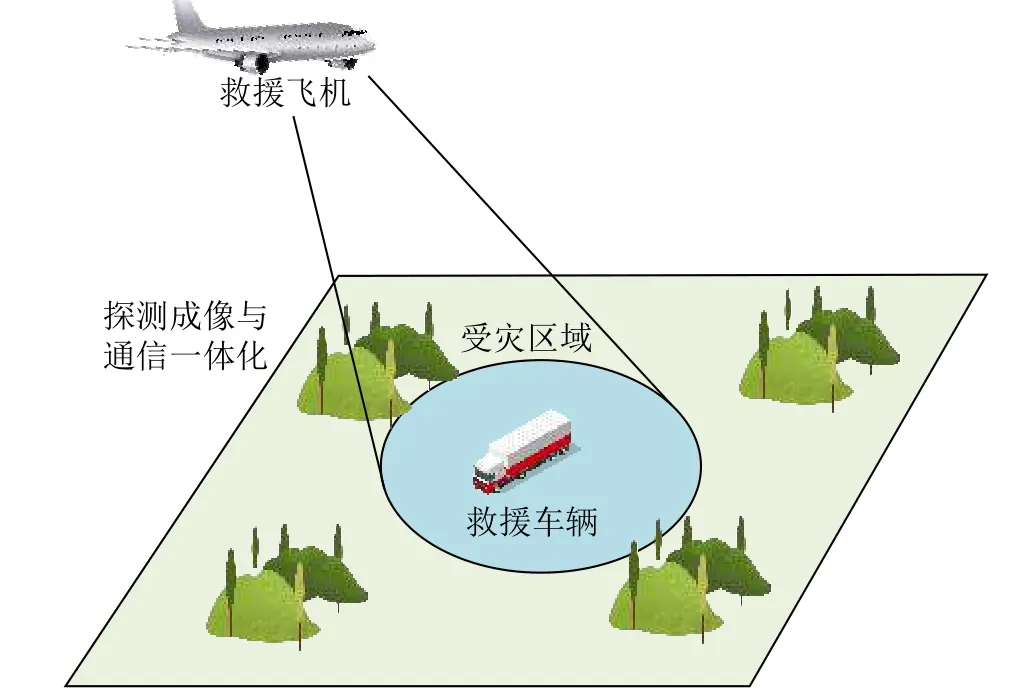
图1 雷达通信一体化系统用于救灾Fig.1 Application of joint radar and communication system in disaster relief

雷达系统与通信系统类似，都具有发射机、接收机等硬件终端，这也是雷达与通信可以实现一体化设计的基础[6]。雷达与通信系统的工作原理如图2所示，两类系统都存在信号发射部分和信号接收部分，并且都是经过无线传输。其区别在于雷达主要是获取目标或者说“信道”的信息，而通信主要是获取信源的信息。目的不同导致雷达与通信系统各自发展的时候，所应用的原理和指标都各不相同，不同功能的领域呈现烟囱式的发展结构。这也为雷达通信一体化设计带来了一些原始壁垒。正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)信号作为4G/5G无线通信的波形，因其具备频谱效率较高、可有效对抗多径效应、子载波调制方式灵活、易于实现等优点和宽带可合成的特性，广泛应用于一体化波形设计中[7–16]。然而，传统的OFDM一体化信号设计中存在一些难以避免的缺点，比如使用循环前缀(Cyclic Prefix,CP)抗多径干扰会降低能量利用率，并产生虚假目标，多载波模式对子载波间正交性要求较高，多普勒频偏对信号正交性影响较大等[17]。本文在此基础上，采用空白保护间隔替代循环前缀，来抑制符号间干扰(Inter-Symbol Interference,ISI)和载波间干扰(Inter-Carrier Interference,ICI)，并利用雷达信号来辅助信道估计，实现信道均衡和补偿多普勒频偏的效果，达到一体化信号协同工作的目的，实现频谱利用率和性能的提升。

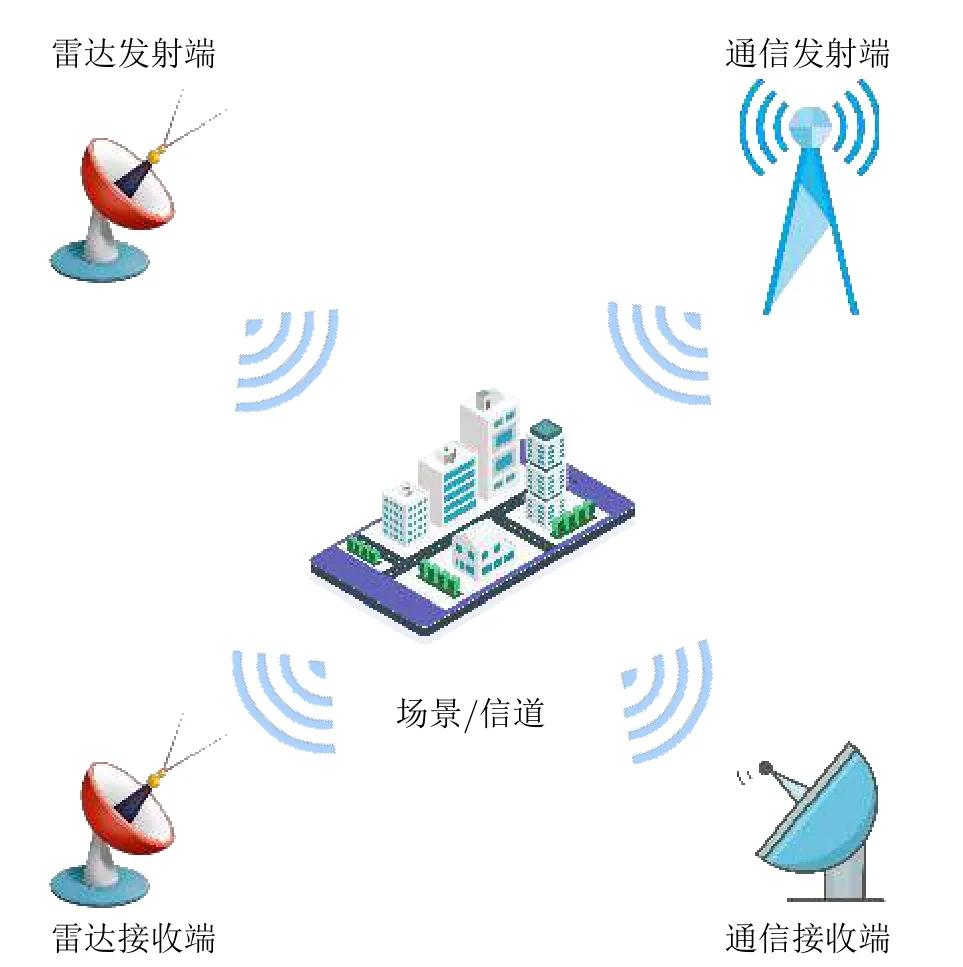
图2 雷达通信系统简图Fig.2 Radar and communication system diagram

本文主要内容安排如下：第2节首先介绍OFDM-chirp信号的发展历程，阐述目前所采用的OFDM-chirp信号用于一体化波形设计存在的一些问题，并提出本文一体化信号的设计方法；第3节详细介绍本文所提出的一体化波形处理方法；第4节为仿真实验，对本文所提方法的有效性进行验证；第5节对全文的工作进行总结。

2 OFDM-chirp信号简介

OFDM-chirp信号，也称为OFDM-LFM信号[18]，最早提出是应用于多发多收合成孔径雷达(Multi-Input Multi-Output Synthetic Aperture Radar，MIMO SAR)中，用于生成两路或者多路正交的信号。其基本原理是将chirp信号分别调制到不同的子载波组上，由于OFDM信号子载波之间是正交的，不同的子载波组上的信号自然也是满足正交性的，这样就可以在发射端和接收端进行分离，从而实现在方位向上形成多个等效相位中心来进行高分辨率宽测绘带的成像。最早提出的基于OFDMchirp的多路正交信号存在一个非常微小的频偏，这在现实实现中存在一定的难度[19]，文献[20]提出了一种改进的OFDM-chirp信号，该信号消除了这一微小频偏，降低了信号产生的难度。改进后的OFDM-chirp信号的生成矩阵为

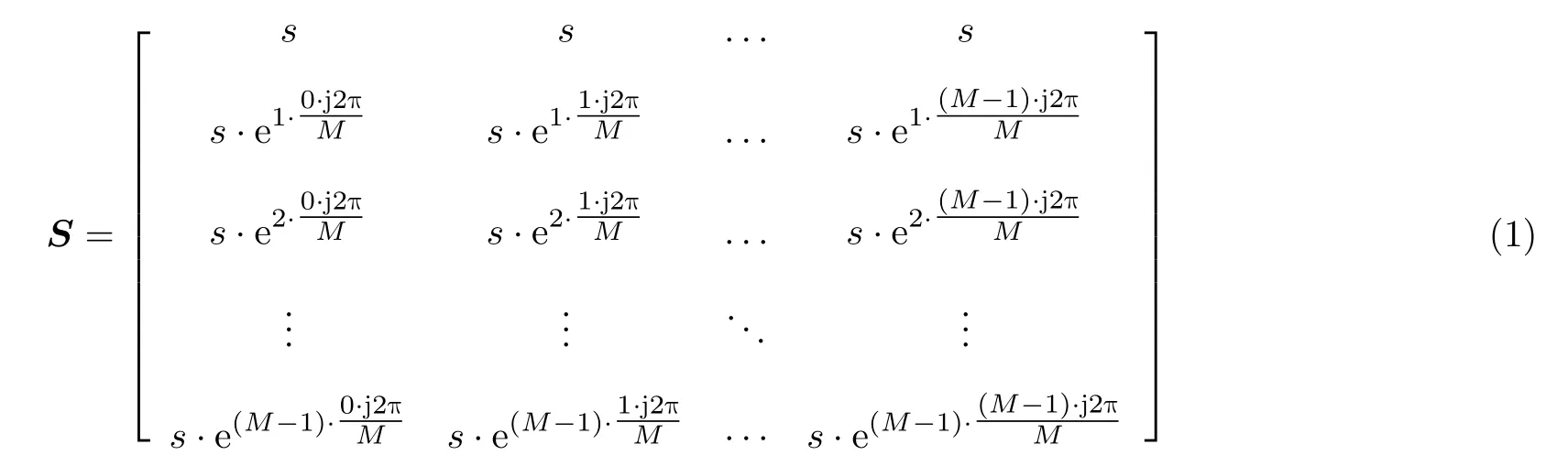
其中，s1为需要调制的通信信号，可以采用二进制移相键控(Binary Phase Shift Keying,BPSK)、正交相移键控(Quadrature Phase Shift Keying,QPSK)等方式调制通信信息。s2为需要调制的雷达信号，一般是线性调频信号。可以表示为

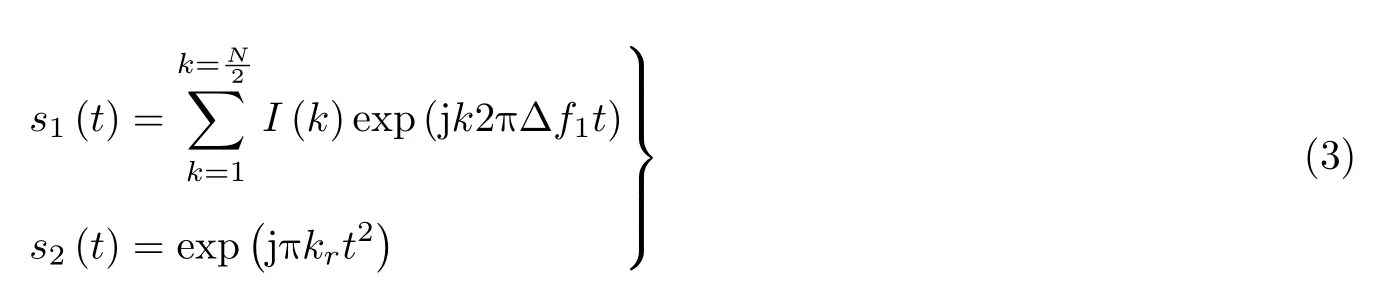
其中，N为总子载波个数，I(k)为调制的通信信息，Δf1为子载波间隔，信号的脉宽为T/2，并且Δf1=2/T。由此可以根据信号生成矩阵得出通信信号和雷达信号的表达式为

其中，rect(·)为矩形窗函数，当0≤x ≤1时，rect(x)=1。T为一体化信号一个符号的时宽。将式(4)变换至频域，可以得到两路正交信号的频域表达式为

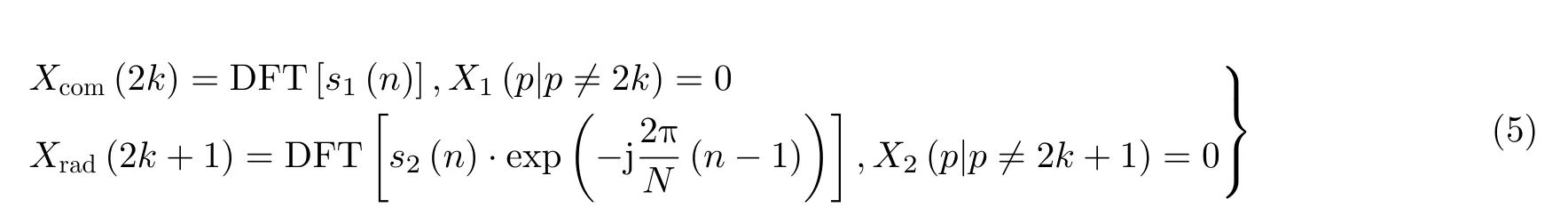
其中，s1(n)为s1(t)的采样序列，s2(n)为s2(t)的采样序列，子载波间隔Δf为Fs/N,Fs为DFT所采用的采样率，p=0,1,2,···,N −1,k=0,1,···,(N/2−1)。

将两路信号相加就可以得到一体化信号的一个符号，图3展示了一体化信号的频域和时域形式。

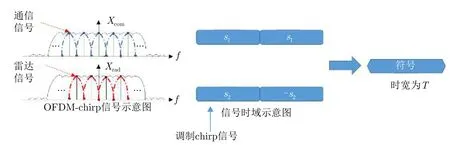
图3 一体化信号符号设计Fig.3 Symbol design of integrated signal

本文所考虑的模型为图1所示模型，机载平台为一体化平台，在保持对场景探测成像的同时可以实现将通信数据传输给地面。对于采用正交波形体制设计的一体化信号而言，功能的权衡体现在能量的分配上。如果总发射功率不变，则其中一种信号能量的增加必然会导致另一种功能信号能量的损失。在一体化波形设计中，通信信号能量主要影响误码率，雷达探测信号能量主要影响探测距离、雷达图像信噪比等，在设计时如果优先保障通信功能则可以将能量资源更倾向于通信信号，如果更注重探测质量，则应分配给雷达探测功能更多的能量。

在文献[3]中，初步介绍了OFDM-chirp信号实现雷达通信一体化的可行性。但是由于通信信号需要加入循环前缀和参考序列等用于抵抗多径干扰以及多普勒频偏，这些额外的开销会降低能量利用率和频谱效率。如果通信信号使用循环前缀而雷达信号不使用循环前缀，这种情况下，此循环前缀会影响子载波之间的正交性。如果奇偶频点分别调制雷达、通信信号以后对整个符号采取循环前缀的设计，则该循环前缀在一个符号时间的积分长度内可以保护子载波之间的正交性。同时带来的问题是，循环前缀对于通信信号而言是为了避免多径效应的影响，该循环前缀的长度由场景最大多径时延决定。对于探测系统而言，为了信号的正交性能，积分区间需要取一个符号的长度，则场景的测绘带宽将受到循环前缀的限制。对于探测信号而言，该循环前缀长度要大于场景最远目标的回波和最近目标的回波到达接收机的时延。对于这种情况，需要循环长度比较长，是对资源的一种浪费。所以本文在此基础上，提出了一种OFDM-chirp一体化信号的设计和处理方法，该方法没有采用传统的添加循环前缀的方法，而是采用了插入空白保护间隔的设计方法，降低了载波间干扰和符号间干扰的同时，实现了能量利用率的提升。并且本文提出了一种利用雷达信号辅助信道估计和多普勒估计的方法，节约了传统通信系统中导频信号和训练序列的开销，仿真分析证明了本文所提方法的有效性。

3 基于OFDM-chirp的一体化信号设计和处理方法

3.1 基于空白保护间隔的OFDM-chirp一体化信号设计方法

当多载波通信系统传输时存在多径效应，会产生ICI和ISI等现象[21]。使用循环前缀可以使接收窗的时间内仅存在一个符号的信号，来消除ISI带来的影响。并且可以利用FFT的循环卷积特性，使接收信号在完整积分区间内各个子载波都是整数个周期，不同的到达时间只让信号发生了相位的变化，从而在进行信道均衡后可以将ICI的影响降到最低。

通过分析，循环前缀主要有两个作用：一个是维持子载波间的正交性，保证积分区间内子载波个数为整数；二是提供保护间隔，将可能存在的其他符号的信号去除。采用空白保护间隔可以满足第二个作用，在接收信号时对信号进行符号分割，保证每个接收窗内仅存在当前符号，则可以实现消除ISI的目的，如图4所示，在加入CP和保护间隔后，ISI均可以得到抑制。对于ICI，可以通过选取合适的时间窗长度，使其大于每个符号的持续时间，而又不至于发生混叠，这样对于整个积分区间，不同子载波的周期数仍然是整数，如图5所示，所以可以抗载波间干扰。假设接收时的采样率为Fq，采样点数为Nm，则经过FFT以后，需要满足 Δf为Fq/Nm的整数倍，才可以准确地将对应子载波的权值解调出来。如果不满足此条件，需要将积分区间补零，直至满足此条件。

图4 抗ISI原理图Fig.4 Schematic diagram of ISI resistance

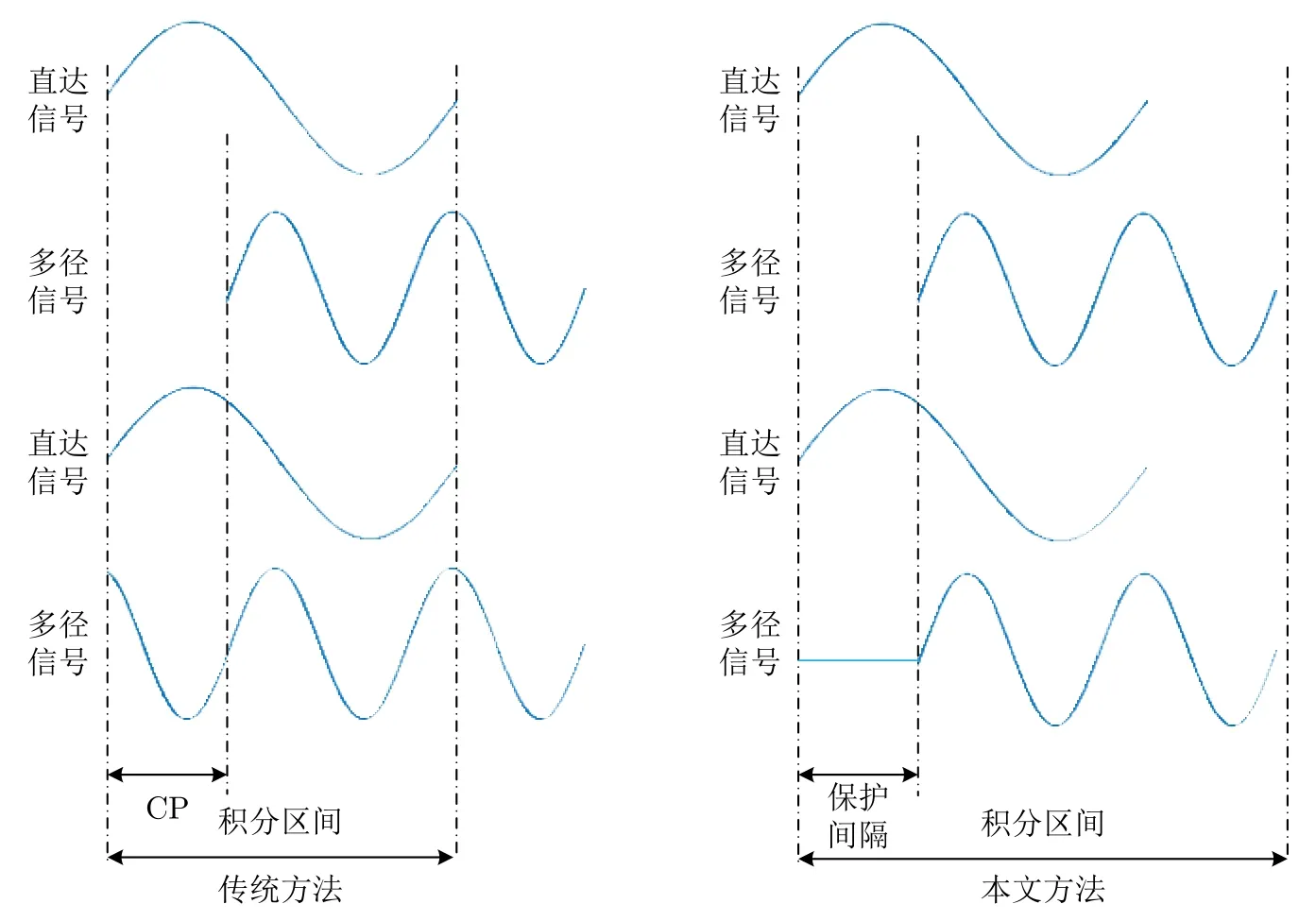
图5 抗ICI原理图Fig.5 Schematic diagram of ICI resistance

3.2 一体化信号处理方法

本文提出的基于OFDM-chirp信号的一体化波形设计和处理方法如图6所示，首先将通信信息经过分组和编码以后与雷达信号一起调制到不同的符号上，经过无线传输和探测场景以后到达接收端。在接收端，首先对接收到的信号进行符号分割和信号补零。利用一体化信号中调制的chirp信号进行多普勒估计，并对频偏进行补偿。在补偿多普勒之后，雷达与通信信号就可以实现正交解调和分离。利用解调出的雷达信号可以进行后续的探测成像处理，并辅助通信信号实现信道估计，从而恢复出原始通信信息。

图6 基于OFDM-chirp信号的雷达通信一体化波形设计与处理流程图Fig.6 Joint radar and communication waveform design and processing flow chart based on OFDM chirp signal

3.2.1 一体化信号探测存在距离模糊现象及补偿方法

由于OFDM-chirp信号解调的时候需要进行频域的抽取，所以采用其进行探测成像时会有固有的距离模糊问题，下面将具体分析其距离模糊成因。

雷达探测和成像等功能需要获取目标的位置信息，距离向的位置信息是利用脉冲压缩以后的峰值位置来确定的。对于一个信号而言，如果在时域仅仅发生了移位或者是循环移位，对应的，其频域信号的幅值不变，而相位会发生变化。而脉冲压缩的频域处理正是利用了这一原理，获取了目标在频域的相位移动特性，并通过傅里叶逆变换到时域，从而得到信号在时域上的平移距离。

在OFDM-chirp信号解调时，需要对频域信号进行抽取。抽取将会导致部分信息的缺失，如果载波上的相位移动超过一个周期，就会发生距离模糊现象。如图7所示，信号在时域发生了平移，相应的，经过傅里叶变换后某一载波的相位也发生了改变。如果相位的改变正好是 2π的整数倍，那么他们在频域抽取以后就无法区别。所以我们需要将探测范围限定在最大不模糊距离以内。在实际系统中，可以结合数字波束成形(Digital Beam Forming,DBF)等技术，来达到这一限制。

图7 距离模糊成因Fig.7 Causes of distance ambiguity

3.2.2 多普勒频移的估计与补偿

OFDM通信系统是多载波系统，多普勒频移对多载波系统的性能影响比较严重。当频偏很小的时候，通信系统的星座图将发生偏移，而随着多普勒频偏的增大，通信系统星座图将发生非常严重的恶化。不仅如此，多普勒频偏还会影响子载波之间的正交性，造成能量的泄漏，这将严重影响雷达探测成像的性能和通信误码率。在OFDM通信系统里，有专门的训练序列用于频率同步的粗估计和精估计，这些额外的开销也将会造成频谱资源的浪费。对于OFDM系统而言，保证子载波间正交性的条件是

T表示信号周期，m和n分别表示不同的子载波序号。对于不同的子载波，在完整的信号周期内两者积分结果为0。当由于物体运动产生多普勒或者发射端和接收端的本振频率存在偏差时，会产生频偏。频偏会使得原本正交的各个子载波之间产生干扰，从而导致信号解调出现错误。

本文设计的发射信号可以表示为

其中，fc为载波频率，sl(t)为基带信号。

不考虑噪声的情况下，在接收端通过去载频和低通滤波器以后的接收信号为

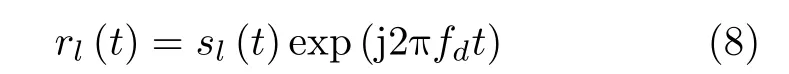
其中，fd为多普勒频偏。

对于一体化信号而言，fd会产生两类影响，一类是破坏子载波的正交性，导致雷达信号与通信信号产生相互干扰，另一类是雷达信号和通信信号各自的子载波间产生干扰，从而影响性能。对于第1类影响，频率的偏移导致各自信号的能量泄漏到另一组子载波上，其能量泄漏与原能量的比值可以用归一化多普勒频偏表示。

定义ε为归一化子载波偏移为频偏与子载波间隔的比值

定义泄漏到另一子载波组的能量与原信号能量之比为

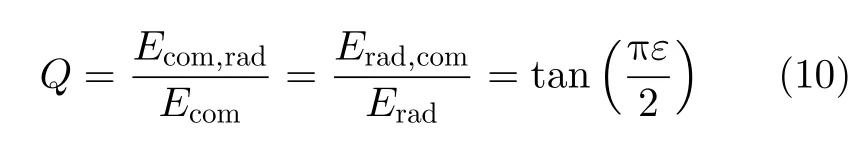
其中，Ecom,rad表示泄漏到雷达子载波中的通信信号的能量，Ecom表示原通信信号的能量，Erad,com表示泄漏到通信子载波中的雷达信号的能量，Erad表示原始雷达信号的能量。这部分能量的泄漏可以近似看作加性噪声，会造成雷达信号的脉冲压缩性能的下降，积分旁瓣比(Integrate the Side Lobe Ratio,ISLR)的恶化，并会造成误码率的上升。

第2类影响是两种功能的信号之间的子载波间存在相互干扰的结果。对于探测信号，该部分影响主要表现为影响脉压结果和峰值的位置，对于通信信号，该部分干扰会使通信星座图发生偏转并最终发生混叠，严重影响通信性能。

首先分析频偏对探测信号的影响，不考虑子载波组间泄漏能量的情况下，解调以后的雷达信号频域形式可以表示为

频域匹配滤波器为

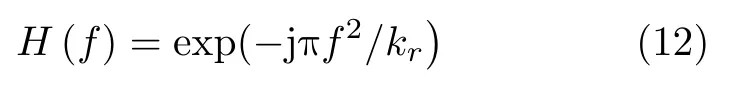
匹配滤波以后

变换至时域以后

可以看出，频偏会影响脉压结果，并影响脉压峰值的位置。

下面对通信信号进行分析，不考虑泄漏能量的情况下，假设发射端调制的通信信号经过采样后为

其中，N为采样点数，Xcom如式(5)所示。

经过多普勒偏移以后的信号为

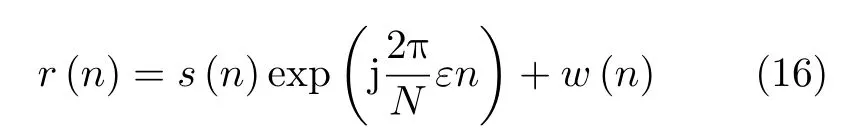
其中，w(n)为噪声序列。

对接收信号做FFT可得

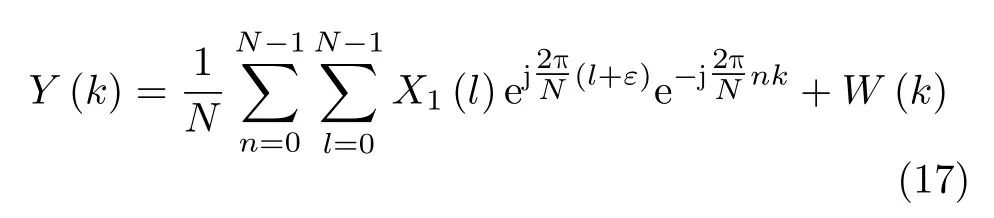
可以得到

其中

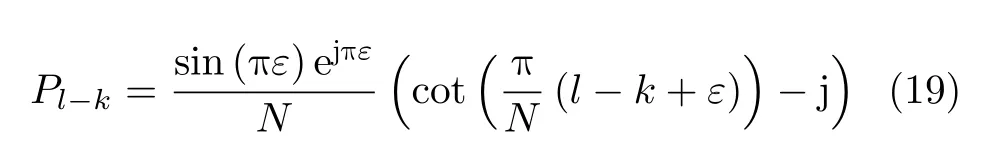
从式(19)可以看出，随着ε的增大，也就是多普勒频移的增大，得到的信号序列与原序列的差距也就越大。对应的星座图的变化如图8所示。星座图从一开始的小幅偏转和弥散，到逐渐混叠，多普勒对通信误码率的影响变得越来越不可忽视。所以需要对多普勒频偏进行补偿。

图8 星座图随着多普勒频移增大的变化特性Fig.8 Variation characteristics of communication constellation with Doppler shift increasing

OFDM系统中，一般采用训练序列来进行时间的同步和频偏的估计。在一体化系统中，如果添加同步序列，也会降低频谱利用率并破坏奇偶载波之间的正交性。所以本文提出可以利用已知的雷达信号进行频偏的估计。在不存在多普勒频偏时，如果直接对雷达信号所在频点进行抽取，并与频域参考信号进行匹配滤波，其功率输出最大。在存在多普勒频偏时，采用前文所述方法进行解调并频域抽取时，由于子载波频率发生偏移，解调时引入了干扰噪声，这对于匹配滤波的功率输出是没有贡献的。所以，找到雷达信号匹配滤波输出最大时的多普勒频率偏移即为多普勒频偏的估计值。

得到多普勒频偏的估计值以后，就可以对信号进行频偏补偿。对已知频偏的信号有两种方法，一种是时域的方法，将信号乘上一个多普勒补偿因子，从而得到补偿以后的信号，如式(20)所示。

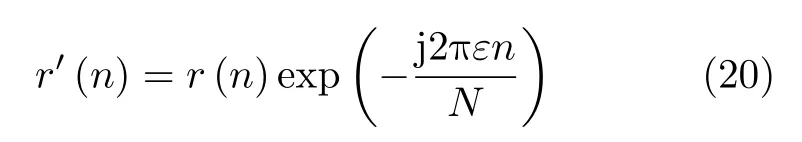
第2种方法是频域方法

如图9所示，在正交解调前，先利用已知的先验信息对频谱偏移进行估计并补偿，之后采用正交解调的方法，就可以将雷达信号和通信信号进行分离。

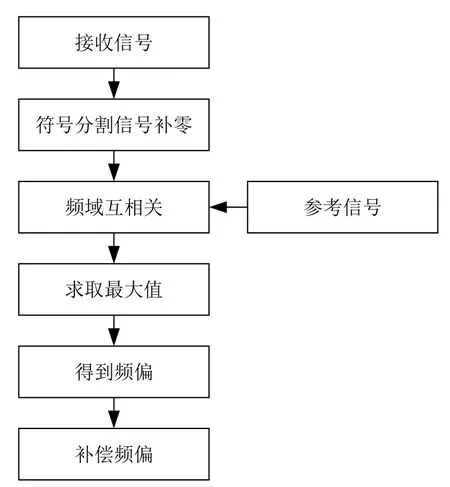
图9 多普勒频移补偿方法流程图Fig.9 Flow chart of Doppler shift compensation method

3.2.3 一体化信号信道估计方法

在接收端补偿多普勒频偏以后，雷达信号与通信信号为两组正交信号，利用其频偏交叉的特性，可以利用雷达信号的先验信息对信道进行估计，并在插值后得到通信信号的信道估计结果，实现信道均衡与同步等操作。用于一体化信号的信道估计方法如图10所示。同时该方法可以很容易地判断哪些子载波上的信号发生了深衰落，从而针对性地使用其他的子载波来进行大数据量的传输。

图10 一体化信号信道估计流程Fig.10 Flow chart of integrated signal channel estimation

3.2.4 一体化信号的峰均功率比的影响

峰均功率比(Peak to Average Power Ratio,PAPR)，也称作峰均比(Peak to Average Ratio,PAR)，其定义如式(23)所示

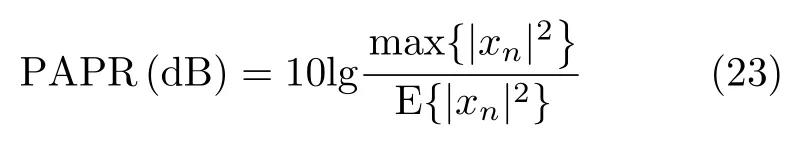
其中，xn为时域信号序列。

由于OFDM采用多载波技术，当各个子载波相位相同时，会出现比较高的峰值功率，从而导致其具有高的峰均功率比。在传统通信领域，通信信号被调制到特定的星座图上，这将导致其多个子载波的相位一定是相同的，从而产生较大的峰值功率。

雷达探测所使用的线性调频信号，通过二次相位调制，保证了其时域恒模的特性，在OFDM子载波上调制二次相位的chirp信号可以有效地降低峰均比。所以使用OFDM-chirp信号进行一体化波形设计时，与OFDM通信信号相比，峰均功率比也会下降。

3.3 使用循环前缀与本文方法信噪比分析

本节主要对使用循环前缀的信号与使用空白保护间隔方法的信噪比进行了对比和分析。

使用循环前缀的信号，假设发射信号每个符号包含的通信信号的能量为Ets，符号持续时间为Tg+Ts，其中Tg为循环前缀长度。接收窗持续时间为Ts，信号传信率为Rb，噪声等效带宽为W，从发射到采样信号经过的信道总衰减为L，其中包含了多径的影响。从而可以得出，对于使用循环前缀的信号，接收信号有用信息的总能量为

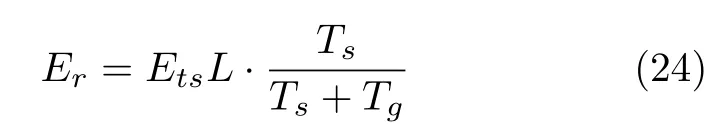
噪声信号的总能量为

其中，Eb表示通信信号的每比特平均功率。

对于使用空白保护间隔的信号，假设其他参数都与使用CP的信号相同，不同的是其符号持续时间为Ts，接收窗持续时间为Ts+Tg。可以得出，接收信号有用信号的总能量为

噪声信号的总能量为

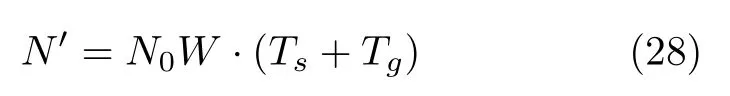
从而可以得出使用空白保护间隔的(Eb/N0)′

从而可以得出结论，使用循环前缀的方法在发射信号的能量利用率上比较低，但是接收时间窗的增加会使使用空白保护间隔的系统噪声能量的增加。如果接收窗持续时间选取与带有CP的信号发射时长一致的时间窗，则在其他条件都相同的条件下，两者的Eb/N0一样。在实际应用中，传统信号还需要训练序列和导频等额外开销，这些开销会进一步降低频谱利用率和能量效率，所以采用本文所提出的信道估计方法可以提升频谱效率和能量利用率。

4 仿真实验

为了验证本文所提的OFDM-chirp雷达通信一体化波形设计和处理方法的有效性，本文设计了仿真实验进行验证。本文仿真参数如表1所示，所采用的通信调制方法为QPSK调制。从图11(c)可以看出，多普勒频偏带来的子载波正交性的破坏造成了积分旁瓣比的抬升。图11(b)可以看出，多普勒同时会带来脉压位置的改变，从而影响了雷达探测性能。图11(c)展示了在不同多普勒频偏的条件下，一体化信号中雷达探测信号积分旁瓣比的变化。图11(d)展示了不同多普勒频偏下通信误码率的结果。可以看到，多普勒频偏会对一体化信号的性能产生严重影响。

表1 仿真参数Tab.1 Simulation parameters

图11 多普勒频偏带来的影响Fig.11 Influence of Doppler-shift

图12给出了多普勒频偏对点目标成像影响的仿真结果。图12(a)展示了使用CP的一体化信号在ε=0.1时的成像结果。图12(b)为使用CP的一体化信号经过多普勒补偿以后的成像结果。图12(c)为本文设计的OFDM-chirp一体化信号在ε=0.1时的成像结果。图12(d)为本文设计的OFDM-chirp一体化信号经过多普勒补偿以后的成像结果。从图12(b)和图12(d)的对比可以看出，本文方法的点目标成像具有较少的模糊能量。图13针对图12(b)和图12(d)的结果给出了距离向切片，其相关指标如表2所示，本文设计信号的探测信号峰值旁瓣比(Peak Side Lobe Ratio,PSLR)为–13.24dB，优于使用CP的一体化信号–10.94dB的PSLR；并且ISLR为–9.67dB，优于传统方法的–6.04dB。

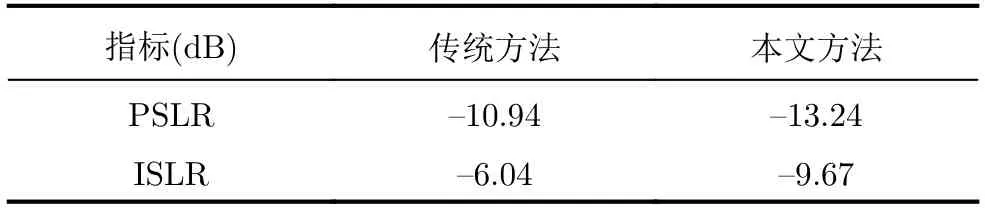
表2 点目标距离向切片指标对比(补偿多普勒后)Tab.2 Index comparison of point target

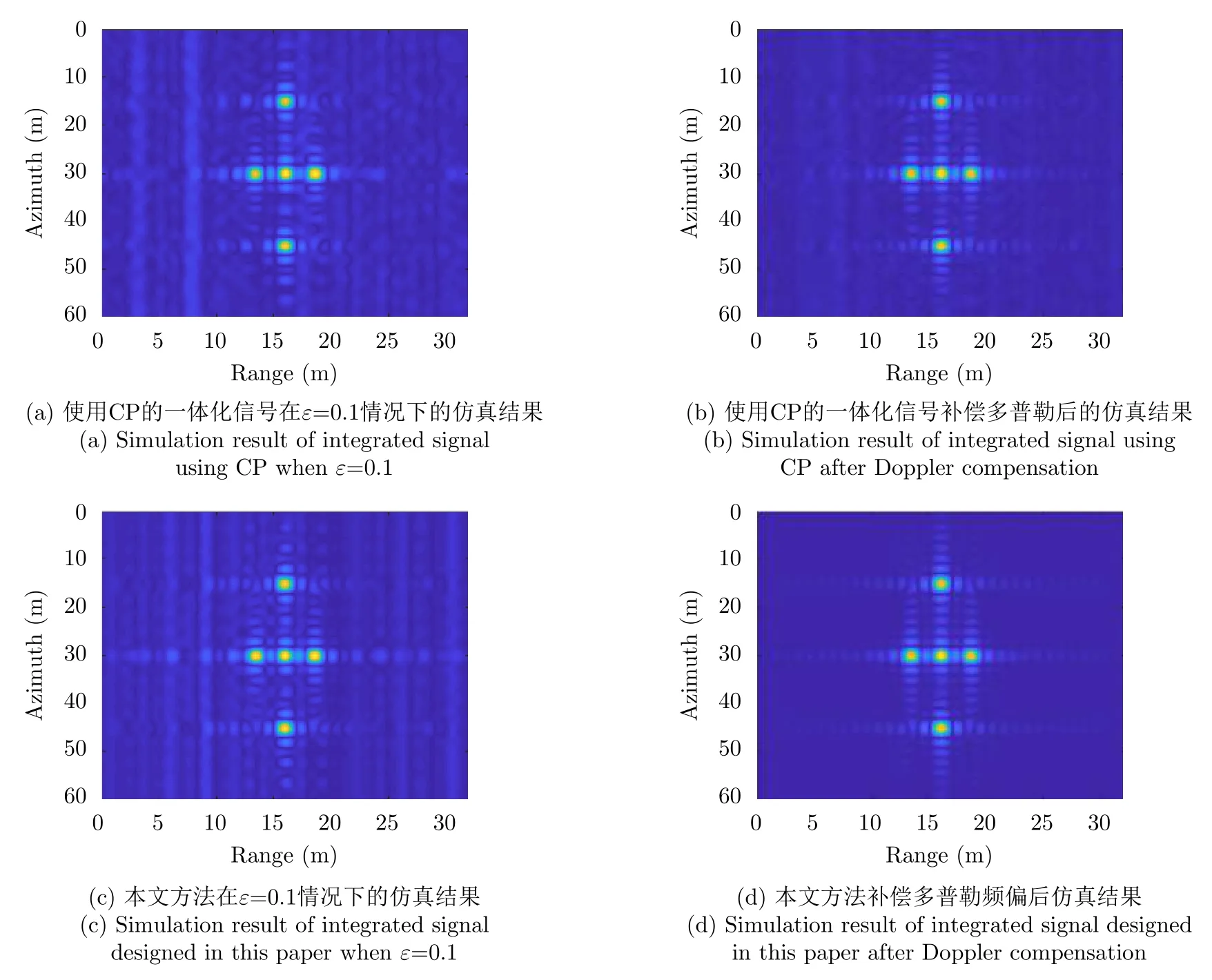
图12 受多普勒影响的点目标成像仿真结果Fig.12 Imaging results of point target affected by frequency offset

图13 点目标距离向切片指标对比Fig.13 Index comparison of point target

图14展示了一体化信号的通信传输仿真结果。图14(a)为传输的原始图像，图14(b)为ε=0.1时接收图像，此时误码率为0.028，图14(c)为经过多普勒补偿和信道估计以后的接收图像，此时误码率为0.00071。可以看出，本文所提出的多普勒补偿方法和信道估计方法可以有效地补偿多普勒频偏和信道失真带来的影响。

图14 通信传输结果Fig.14 Results of communication transmission

图15给出了使用CP和本文方法在无多普勒频偏时，每个符号的信号能量、噪声功率谱密度一样情况下的误码率性能表现，其中蓝色线条表示理论误码率，采用调制方式为QPSK。仿真结果表明，一体化波形的通信传输性能与理论误码率比较吻合。

图15 通信误码率与Eb/N0的关系Fig.15 The relationship of communication error rate andEb/N0

图16给出了在多径情况下本文方法与使用CP方法的性能对比。在此仿真中，调制方式为QPSK，多径信号对应的距离为[0192m384m]，多径信号功率比为[1 1 1]。传统方法的循环前缀Tg=Ts/4，并使用了1/4的子载波调制导频信号。可以看出，在存在多径时直接解调的误码率非常高，在进行信道估计以后，误码率性能得到了提升，并且采用本文提出的方法后，误码率性能要优于使用循环前缀并采用1/4子载波调制导频信号的传统方法。而且本文方法不需要导频信号，与传统方法相比，提升了频谱效率和能量利用率。

图16 多径情况下误码率性能对比Fig.16 BER performance comparison in the presence of multipath

图17给出了QPSK调制下，OFDM-chirp一体化信号与通信信号的峰均功率比的概率密度分布函数。图17(a)、图17(b)、图17(c)分别给出了64个子载波、256个子载波和512个子载波下的PAPR对比情况，其中C表示通信信号，JRC表示一体化信号。从图17可以看出，随着子载波个数的增加，峰均功率比变大的概率更高；与OFDM通信信号相比，采用OFDM-chirp调制以后，一体化信号的峰均比约下降4dB，这对于提高通信性能具有非常重要的意义。在更低的峰均比下，功率放大器的性能可以得到更大的释放，从而在实际应用中可以发射更大功率的信号。

图17 不同载波个数下的一体化信号的峰均功率比Fig.17 Peak to average power ratio of integrated signal with different number of carriers

5 结论

本文针对雷达通信一体化波形设计和处理方法开展了研究，提出了一种新的基于OFDM-chirp信号的一体化波形设计方法，分析了该方法设计的一体化信号在多普勒频偏存在时的性能退化机理，提出了相应的补偿方法和信道估计方法，并利用仿真实验进行了验证。其优点如表3所示。传统方法采用循环前缀的设计来降低ICI和ISI，但是会影响雷达的探测性能。本文提出的方法与传统波形设计方法相比，没有采用循环前缀的设计，而是采用空白保护间隔，避免了虚假目标的同时，提升了能量利用率，仿真表明该方法在不影响通信性能的情况下提升了雷达探测成像的性能。在QPSK的条件下，与OFDM通信信号相比，一体化信号的峰均比约降低4dB。本文提出的一体化波形的处理方法可以有效地对抗多径效应和多普勒频偏，存在多径的信道可以被有效的估计，并且补偿频偏以后误码率大大降低。本文所提方法在点目标成像方面，PSLR由传统方法的–10.94dB降低至–13.24dB，ISLR由–6.04dB降低至–9.67dB。仿真实验验证了以上结论。

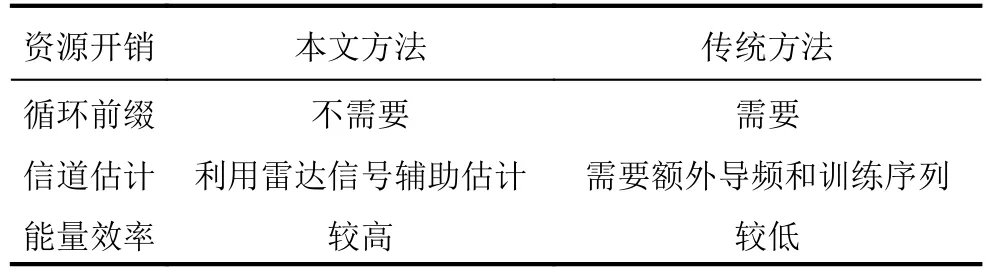
表3 本文方法与传统方法对比Tab.3 The comparison between traditional method and the method proposed in this paper