部分均匀环境下适用于空间对称线阵的修正广义似然比检测方法

闫林杰 郝程鹏* 殷超然 孙苇轩 侯朝焕

①(中国科学院声学研究所 北京 100190)

②(中国科学院大学 北京 100049)

1 引言

近年来，高斯干扰背景下的多通道点目标自适应检测技术在机载雷达领域受到越来越多的关注。早在1973年，Brennan等人[1]就开始了多通道信号检测的研究，随后王永良等人[2]也开展了相关研究工作，并首次在机载雷达领域提出空时自适应处理理论。该技术通过在空-时域进行联合滤波，有效地补偿了平台的运动效应，具有出色的杂波抑制性能。在此基础上，以杂波抑制和目标检测为主要目的的空时自适应检测(Space-Time Adaptive Detection,STAD)技术[3]得到快速发展，许多经典的检测方法被不断提出，主要包括广义似然比检测(Generalized Likelihood Ratio Test,GLRT)[4,5]、自适应匹配滤波检测(Adaptive Matched Filter,AMF)[6]、Rao[7,8]检测和Wald[8,9]检测等。特别地，这些方法均可以自适应地调整检测阈值以维持虚警概率(Probability of false alarm,Pfa)不随外界均匀干扰环境变化，具有恒虚警(Constant False Alarm Rate,CFAR)特性[10]。然而受信号能量起伏、杂波散射等因素的影响，实际应用中均匀辅助数据数量十分有限，由此部分均匀环境(Partially Homogeneous Environment,PHE)下的CFAR检测方法提出，如自适应相干估计器(Adaptive Coherence Estimator,ACE)[11]等。这里部分均匀指待检测数据与辅助数据的干扰协方差矩阵结构相同仅差一个未知的能量比例因子。

以上STAD方法需要对高维度的协方差矩阵进行估计和求逆，对辅助数据的需求量大且计算复杂度高。为解决这一问题，许多改进方法被提出。文献[12,13]指出当雷达系统使用空间对称分布的线阵时，得到的干扰协方差矩阵具有先验的斜对称结构，即矩阵的元素关于主对角线共轭对称，关于副对角线对称。该先验知识意味着只需使用原来一半的参数就可以表征未知的干扰协方差矩阵，大大降低了对辅助数据数量的依赖。基于该特性，一系列斜对称检测方法提出。例如，文献[14]基于GLRT准则设计了部分均匀环境下的斜对称G L R T(Persymmetric GLRT,P-GLRT)方法，文献[15]基于两步GLRT准则提出了斜对称ACE(Persymmetric ACE,P-ACE)方法，这些方法均提高了经典STAD在辅助数据数量受限时的检测性能。针对辅助数据数量不足时的检测问题，基于降秩技术[16]、信号子空间变换技术[17]、Krylov子空间技术[18]以及利用杂波谱的对称特性、贝叶斯模型等其他先验知识[19–26]的STAD方法也可以作为降低辅助数据数量的有效手段。

此外，现有的STAD技术大都基于理想的目标采样模型，即采样点恰好落在目标回波匹配滤波输出的峰值处，不存在任何能量泄漏。然而，当一个点目标跨坐于两个连续的距离单元时，采样时刻很难完全对准峰值位置。为弥补能量泄漏损失，中国科学院声学研究所郝程鹏课题组与意大利教授Orlando等人[27,28]基于目标能量泄漏采样模型提出了一系列修正方法，主要包括均匀环境下的修正GLRT(Modified GLRT,M-GLRT)、修正AMF(Modified AMF,M-AMF)以及部分均匀环境下的定位GLRT(GLRT with Localization Capabilities for PHE,GLRT-LC-PHE)、修正ACE(Modified ACE,M-ACE)等检测方法，这些检测方法除了提高目标检测能力外，还兼具对待检测单元内目标距离的估计能力。文献[29–31]在这些方法的基础上联合使用干扰协方差矩阵的斜对称特性，提出了部分均匀环境下的斜对称修正AMF(Persymmetric Modified AMF for PHE,PM-AMF-PHE)和改进的PM-AMF-PHE(Modified PM-AMF-PHE,MPM-AMF-PHE)等检测方法，进一步提高了小样本辅助数据下的检测性能。

本文在MPM-AMF-PHE[31]方法的工作基础上，在部分均匀高斯干扰背景下提出了一种适用于空间对称线阵的斜对称修正GLRT(PM-GLRT for PHE,PM-GLRT-PHE)检测方法。首先给出了与MPM-AMF-PHE相似的离散接收信号模型，即对目标信号采用目标能量泄漏采样模型，干扰信号采用斜对称先验结构。在检测方法的设计阶段，相比MPM-AMF-PHE方法，PM-GLRT-PHE方法在一步GLRT准则下联合使用待检测数据和辅助数据得到部分均匀环境中能量比例因子γ的数值解法，代替了MPM-AMF-PHE方法中仅使用待检测数据的次优估计结果，进一步提高了参数的估计精度以及对回波数据的利用率，进而获得更优的目标检测性能。最后，将所有未知参数的最大似然估计(Maximum Likelihood Estimate,MLE)结果代替理论值代入GLRT检测统计量中，得到最终的PM-GLRTPHE检测方法。仿真结果显示，PM-GLRTPHE的Pfa相对于背景参数的变化并不敏感，具有CFAR特性，并且相比于其同类型的检测方法在辅助数据数量受限时有着稳健的检测性能优势。

2 问题描述

2.1 接收信号模型

本节对接收回波的离散时间信号模型进行介绍。考虑一个由Na个阵元组成的均匀线列阵，发射的时域脉冲数为Np，每个阵元的发射信号可以简单写为

其中，Re()表示取实部运算，A表示复振幅，p(t)表示矩形脉冲，T为脉冲重复间隔，fc为载波频率。接收信号经过下变频到基带、匹配滤波、采样等一系列预处理后，得到N=NaNp维复矢量。假设Np=1，则单脉冲下第i个距离单元的回波数据可描述为

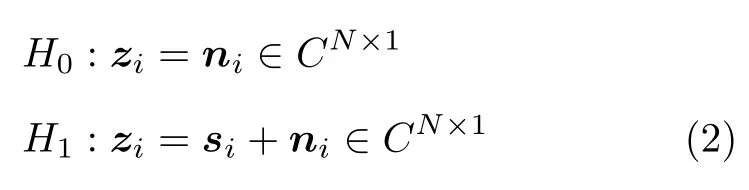
其中，C表示复数域，H0和H1分别表示无目标和有目标的假设，ni表示仅包含白噪声和杂波的复高斯干扰矢量，si表示目标信号矢量。由文献[31]可知，当存在能量泄漏时，目标能量会泄漏到相邻距离单元中，由此得到由邻近距离单元组成的目标能量泄漏采样模型

其中，α表示目标信号的复幅值因子，χp()表示复模糊度函数，Tp为信号脉宽，ε ∈[−Tp/2,Tp/2]为导致目标能量泄漏的剩余时间延迟，f为多普勒频移，表示归一化空域导向矢量，νs表示归一化空间频率，()T表示转置运算，l为待检测单元序号。

2.2 假设检验构建

基于离散时间模型，目标能量泄漏采样模型下的目标检测问题可表述为以下2元假设检验

其中，zi ∈CN×1表示待检测数据矢量。nk,zk ∈CN×1表示从待检测数据相邻的距离单元收集到的K个独立同分布的辅助数据，为保证干扰协方差矩阵的非奇异性，需满足K ≥N。ni为待检测数据中的干扰成分，它与zk之间统计独立，且均服从零均值的多元复高斯分布，即ni～CNN(0,γM)和zk～CNN(0,M)，唯一不同的是两者协方差矩阵相差一个未知的能量比例因子γ(γ >0)。

此外在使用空间对称线阵的主动雷达检测系统中，其干扰协方差矩阵M和导向矢量v均具有斜对称特性。即满足M=JNM∗JN,v=JNv∗，其中()∗表示共轭运算，JN为N维置换矩阵，有

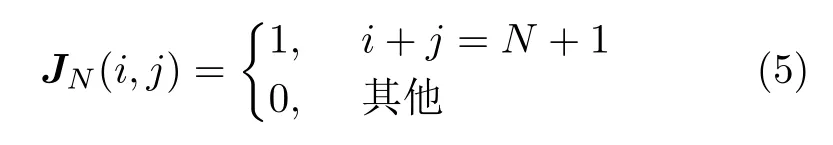
3 检测方法设计

为求解式(6)中的假设检验问题，下面采用GLRT准则设计斜对称泄漏模型1在本文中，将接收回波中目标信号采用目标能量泄漏采样模型、干扰信号采用斜对称先验结构的接收信号模型统称为斜对称泄漏模型。下的自适应检测方法PM-GLRT-PHE。MPM-AMF-PHE方法单独使用待检测数据估计未知参数γ，得到的参数估计精度有限，限制了该方法的检测性能。为进一步提升辅助数据数量受限情况下的目标检测性能，PM-GLRT-PHE将联合待检测数据和辅助数据实现检测统计量的推导和未知参数M,α和γ的MLE，以获得更高的检测性能。为便于推导，令ZK=[z1z2··· zK]∈CN×K表示辅助数据矩阵，Z=[zl−1zl zl+1ZK]∈CN×(3+K)表示联合数据矩阵。GLRT准则下的检测表达式为

其中，η表示一定Pfa下的检测阈值，根据文献[31]可知，fj(Z;jε,jα,γ,M)表示待检测数据和辅助数据在Hj,j=0,1假设下的概率密度函数

其中，t1=−Tp −ε,t2=−ε,t3=Tp −ε为剩余时间延迟。

根据文献[31]，参数Mj在Hj,j=0,1假设下的MLE结果为

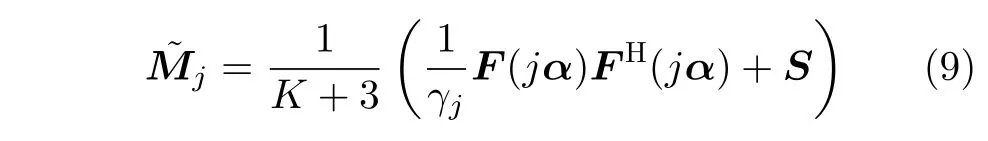
其中，γj,j=0,1表示Hj假设下的能量比例因子。将式(9)代入式(6)，此时的GLRT检测等价为

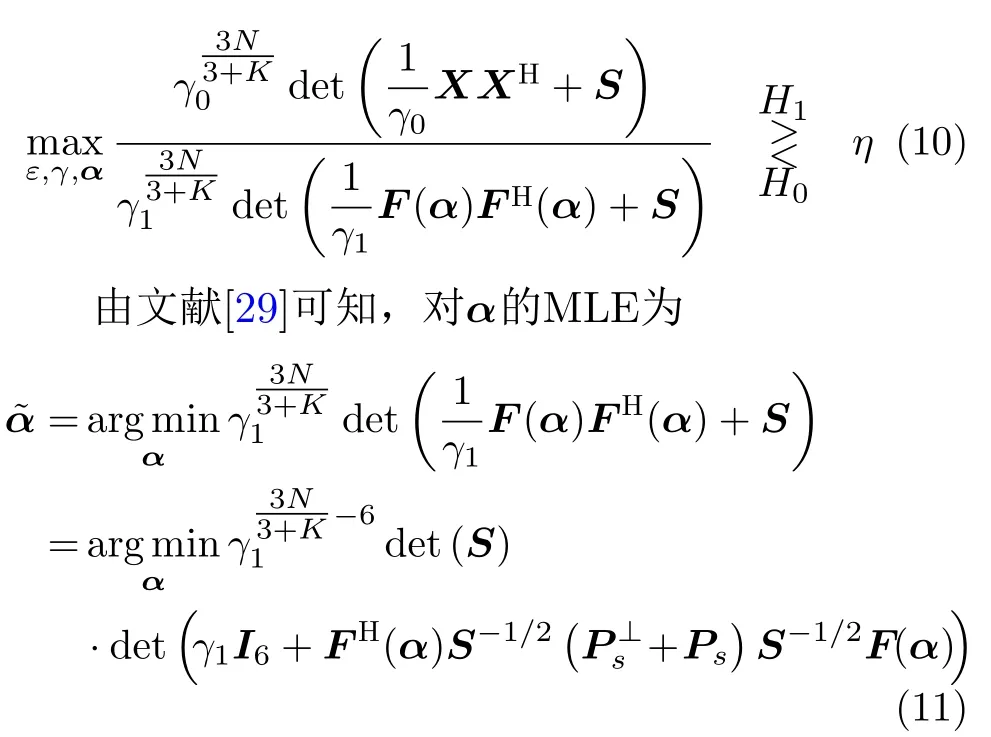
其中，Ps=S−1/2vvHS−1/2/(vHS−1v)表示由S−1/2v张成的子空间的投影矩阵，表示矩阵Ps的正交补，I6和IN分别表示6维和N维的单位矩阵。为了化简式(11)，将第2个行列式展开后的前两项写作

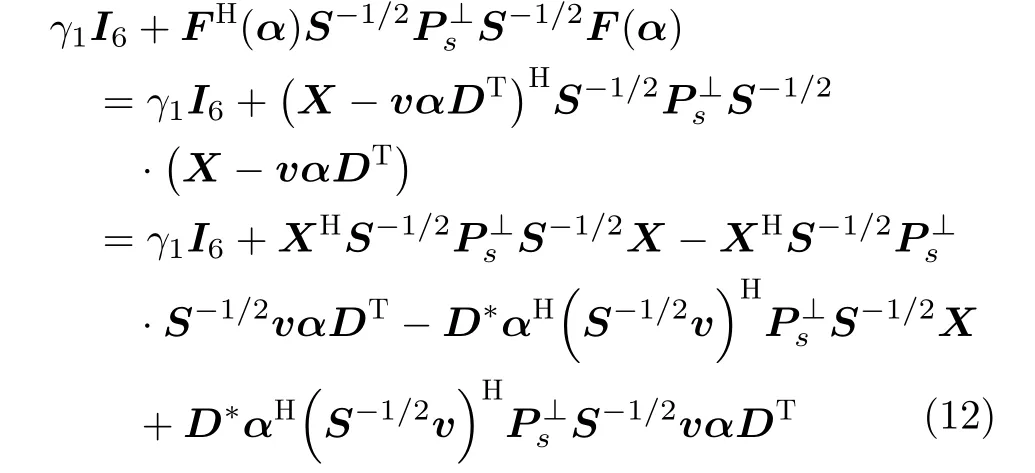
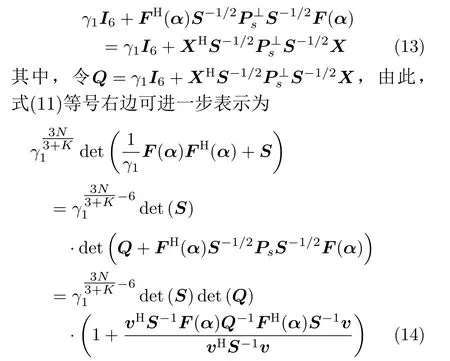
参考文献[29,31]可得α的估计结果为

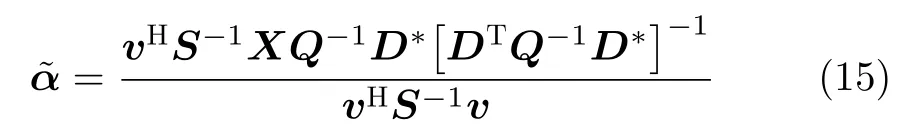
将式(15)代入式(14)，式(14)等价为

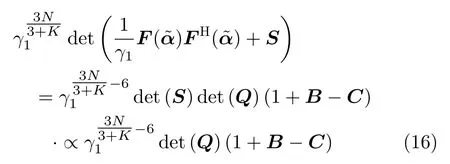
其中，

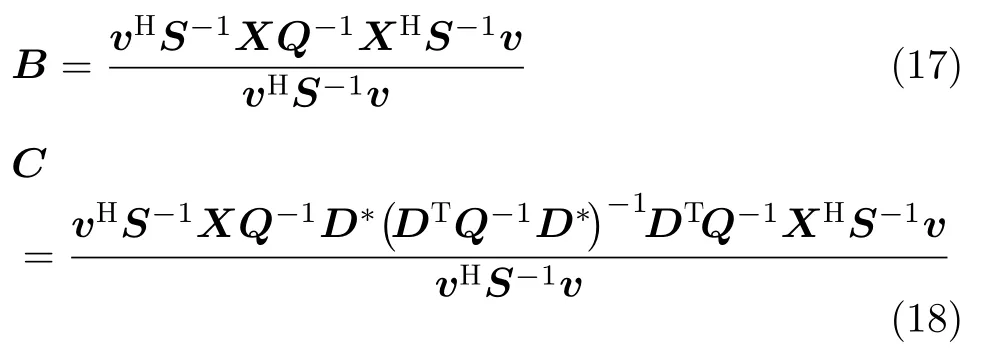
接下来求H1假设下γ的MLE，得到

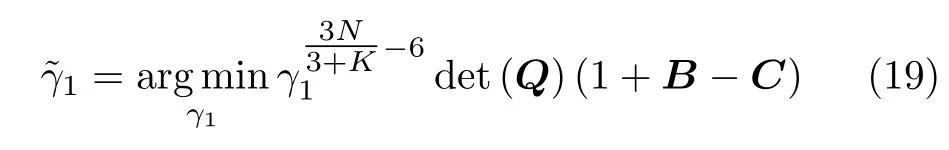
对Q特征分解得Q=U(γ1I6+Λ)UH，其中U ∈C6×6为酉矩阵，Λ为特征值为λ1,λ2,···,λ6的对角阵。将特征分解代入式(19)中

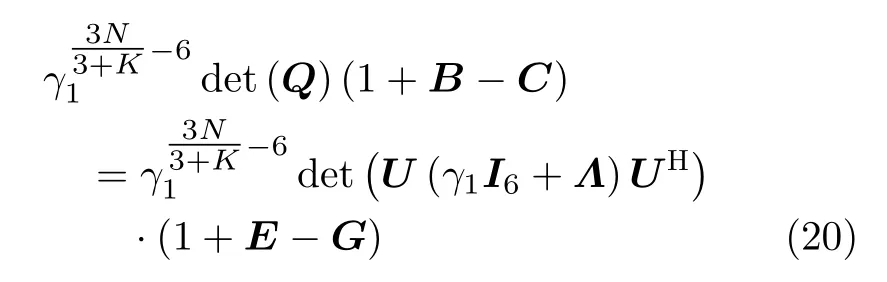
其中，

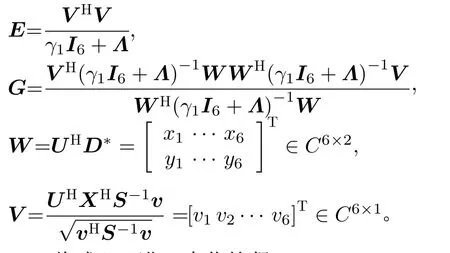
将式(20)进一步化简得

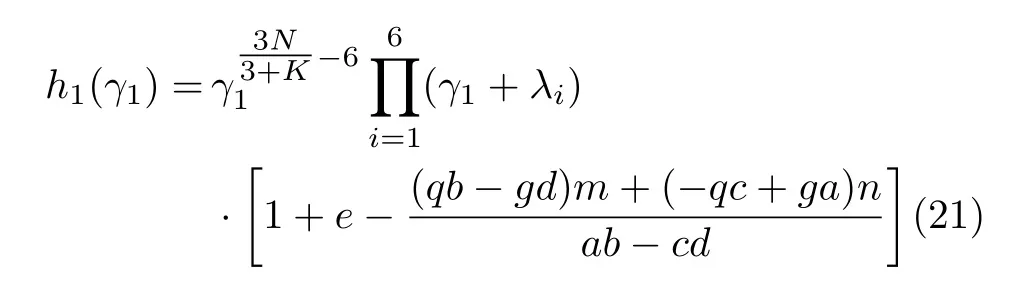
其中，

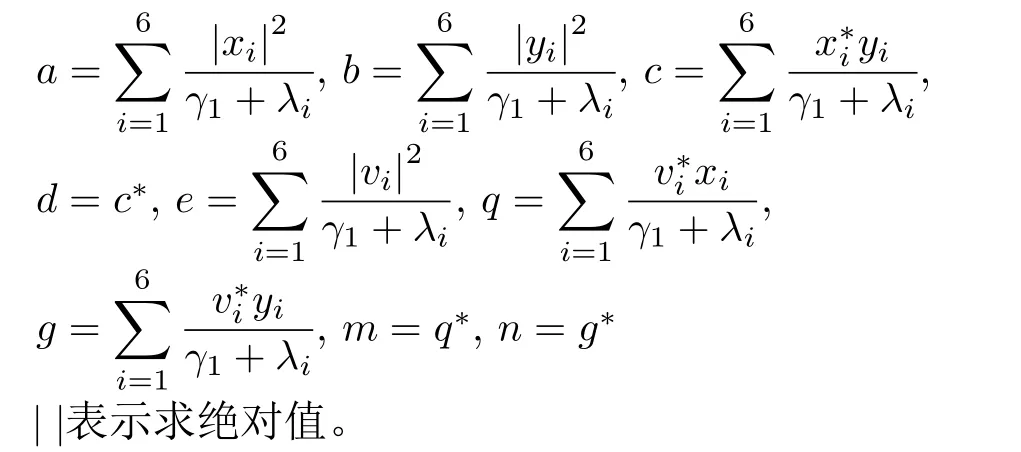
通过对式(21)求关于γ1的1阶导数并置0，可得到估计值。需要说明的是，未给出解析解的形式，因此需要采用数值方法求解，例如可以采用fsolve函数求解此非线性方程。

基于式(10)，在H0假设下对γ0的MLE为

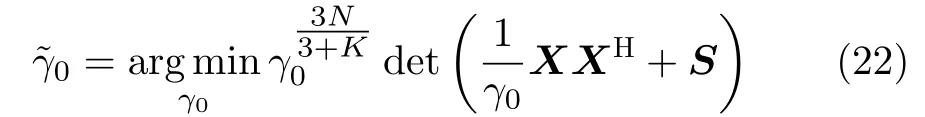
化简得到

对XHS−1X进行特征分解，得XHS−1X=其中U0∈C6×6为酉矩阵，Λ0为特征值为λ0,1,λ0,2,···,λ0,6的对角阵。将其代入式(23)，化简得到

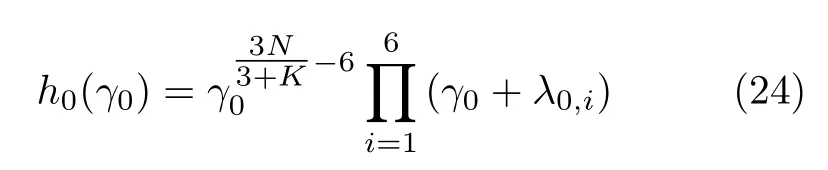
同样对式(24)求关于γ0的1阶导数并置0，通过采用数值方法可以获得估计值

将式(15)、式(21)和式(24)得到的估计结果代替式(10)中的真实值，最终得部分均匀环境下的PM-GLRT-PHE检测方法

需要说明的是，由于文中未能给出对剩余时延ε估计的解析解，进而采用格搜索方法进行估计。格搜索精度定义为∆=Tp/(2Nε)，其中2Nε为均匀分布在[−Tp/2,Tp/2]上的取值。由估计结果可以得到目标距离估计为其中tmin为采样初始时刻，c0=3×108m/s为电磁波传播速度，且估计结果ε˜的精确度最终体现为待检测距离单元内的目标距离估计均方根误差上，即δrms=为仿真次数。

4 性能分析

下面采用蒙特卡罗方法分析P M-G L R TPHE在部分均匀环境下的CFAR特性以及目标检测和距离估计性能。假设系统采用等间距的均匀线列阵，阵元数Na=N=12，信号脉宽Tp=0.2 µs，目标的波达角度为0°，多普勒频移f=0,Nε=5，白噪声能量σ2=1，杂波噪声比(Clutter-to-Noise Ratio,CNR)为30dB。最后，干扰协方差矩阵建模为M=IN+CNRMc，其中Mc(i,j)=ρ|i−j|为基于指数相关复高斯模型的杂波协方差矩阵，ρ=0.9为一步滞后系数，信号杂波噪声比(Signalto-Clutter-plus-Noise Ratio,SCNR)SCNR=|α|2vHM−1v/γ。

4.1 CFAR特性

由于以上推导中未能给出检测方法关于Pfa的解析表达式，为验证PM-GLRT-PHE的CFAR特性，本节给出了Pfa随着背景参数，即能量比例因子γ和干扰协方差矩阵M的变化趋势，通过数值变化的平稳程度来体现Pfa关于这两个参数的鲁棒性。图1给出了PM-GLRT-PHE的Pfa随γ的变化曲线，假设辅助数据数量受限，即K=N+1，预设Pfa=10−3。由图中所示，当γ由2增大至16时，Pfa始终稳定在10−3左右，这说明Pfa独立于γ，即检测方法关于γ是CFAR的。

图1 PM-GLRT-PHE的 Pfa随 γ的变化曲线Fig.1 Pfaagainstγ for the PM-GLRT-PHE

为验证M与Pfa之间的CFAR关系，表1通过固定γ不变，加入不同数量和波达角度的类噪声干扰产生5种不同的仿真情景，以计算不同M值下检测方法PM-GLRT-PHE的阈值η。其中η的仿真次数为100/Pfa,K=N+1,γ=2,Pfa=10−3，干扰噪声比为30dB。从表1可见，在不同仿真场景下PMGLRT-PHE的η值均稳定在2附近。由于η与Pfa呈一一对应关系，因而可以说明检测方法的Pfa不会随着M而改变，即该方法关于M是CFAR的。此外，为进一步证明PM-GLRT-PHE相对于M的CFAR特性，图2给出了Pfa随杂波协方差矩阵Mc中参数ρ的变化曲线，假设K=N+1,γ=2，预设Pfa=10−3。结果表明，当ρ由0.1增大至0.9时，Pfa始终稳定在10−3左右，即所提出方法关于M是CFAR的。

图2 PM-GLRT-PHE的 Pfa随 ρ的变化曲线Fig.2 Pfaagainstρ for the PM-GLRT-PHE

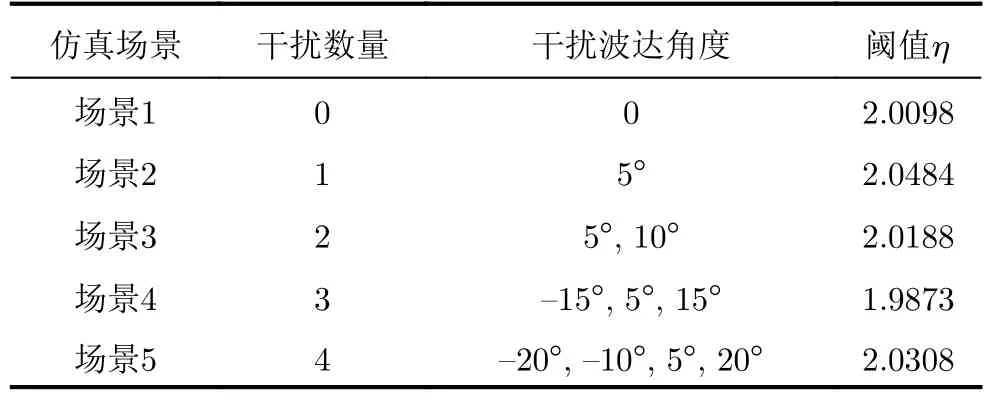
表1 不同场景下PM-GLRT-PHE的阈值Tab.1 Thresholds of PM-GLRT-PHE in different cases

4.2 目标检测和距离估计性能

由于K≥N，首先考虑辅助数据数量受限(K=N+1)的情况，并将已有的斜对称修正检测方法MPM-AMF-PHE,PM-AMF-PHE，以及基于GLRT准则的修正检测方法GLRT-LC-PHE和斜对称检测方法P-GLRT一同仿真。图3中检测概率(detection Probability,Pd)和距离估计的均方根误差δrms的仿真次数均为3×103,γ=2,Pfa=10−4。

图3(a)给出了不同检测方法的Pd随SCNR的变化曲线。结果显示，所有方法的Pd均随SCNR的增大而提高，且PM-GLRT-PHE具有最高的检测概率。例如，在Pd=0.9时，PM-GLRT-PHE优于MPM-AMF-PHE,PM-AMF-PHE,P-GLRT和GLRT-LC-PHE各约1.0dB,1.6dB,4.0dB和10.0dB的性能增益。由此证明PM-GLRT-PHE相比现有的同类型检测方法，有明显的目标检测优势。图3(b)给出了各检测方法的δrms随SCNR的变化曲线。特别地，由于P-GLRT不具备距离估计能力，故未对其距离估计精度进行评估。图中显示，PM-GLRTPHE,MPM-AMF-PHE和PM-AMF-PHE的δrms值大致相同，且三者的距离估计精度均优于GLRTLC-PHE。这是因为PM-GLRT-PHE、MPMAMF-PHE和PM-AMF-PHE检测方法对ε的估计精度相近，且斜对称特性的使用大大提高了辅助数据数量受限情况下对ε的估计准确度。受格搜索精度∆的限制，在高SCNR处，4种检测方法的距离估计误差最终趋于

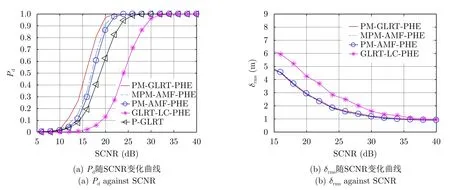
图3 辅助数据数量受限时的目标检测和距离估计性能Fig.3 Detection and range estimation performance with small number of auxiliary samples

为了探索部分均匀环境下的能量比例因子γ对检测性能的影响，图4给出了不同γ下各检测方法的Pd随SCNR的变化曲线，其他参数仍与图3中一致。由图4看出，各检测方法的Pd并不会随着γ取值的不同而产生明显变化，它们均保持与图3(a)中相同的目标检测性能。为了更加直观地展示γ与Pd之间的关系，图5给出了SCNR=18dB时各检测方法Pd随γ的变化曲线。可以看出，随着γ的增大，所有方法的Pd均稳定在图3(a)中SCNR=18dB时对应的值附近，进一步证实了图4中的结论。以上结果说明，各方法的目标检测性能不会随γ的变化而变化，在γ不同的部分均匀环境中，PM-GLRTPHE均能保持稳健的检测性能优势。在参数设置与图5相同的情况下，图6、图7给出了不同γ下各检测方法的δrms变化曲线。由图中看出，各检测方法的δrms同样不会随着γ的变化而变化，若不考虑仿真中随机性的影响，它们的距离估计性能与图3(b)基本一致，例如在SCNR=18dB时，PM-GLRT-PHE,MPM-AMF-PHE和PM-AMF-PHE的δrms均约为3.8m,GLRT-LC-PHE的δrms约为5.1m。

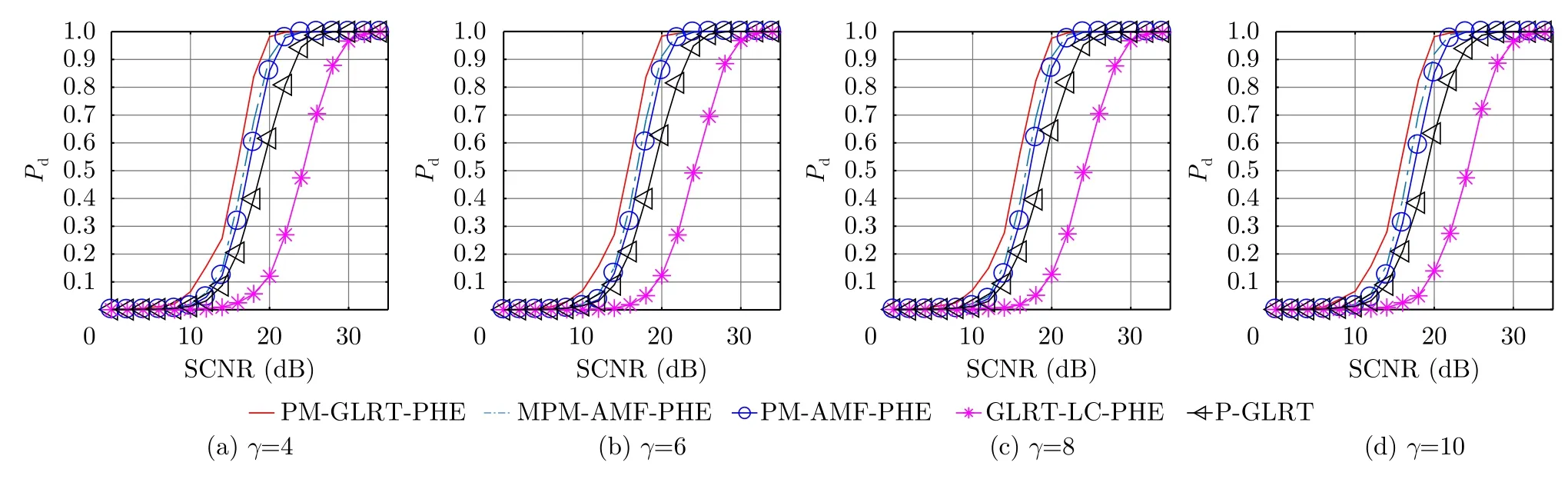
图4 不同 γ下各检测方法的 Pd随SCNR的变化曲线Fig.4 Pdagainst SCNR f or each detection method under differentγ

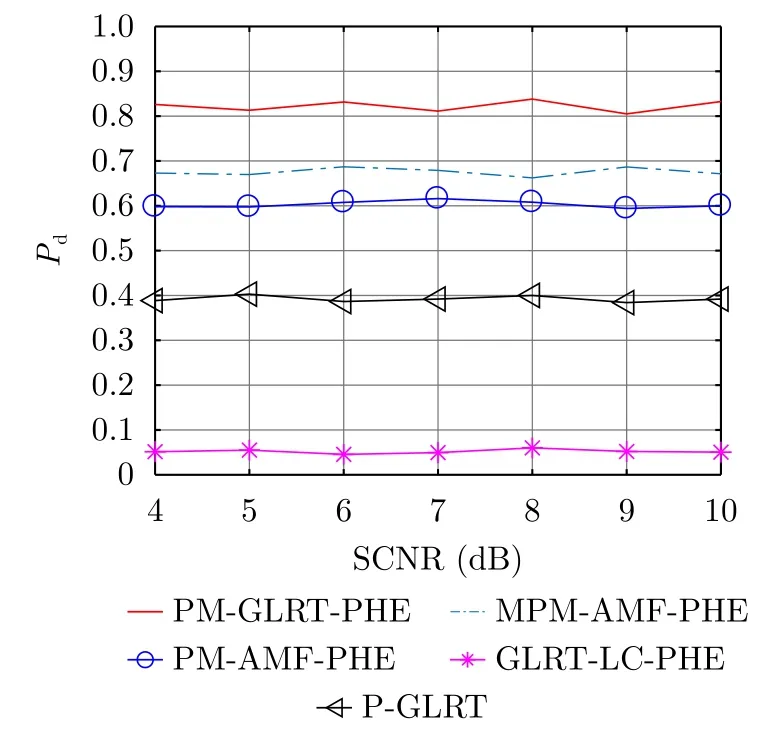
图5 SCNR=18dB时下各检测方法的 Pd随 γ变化曲线Fig.5 Pdagainstγ for each detection method when SC NR=18d B

图6 不同 γ下各检测方法的δrms随SCNR的变化曲线Fig.6 δrmsagainst SCNR for each detection method under differentγ

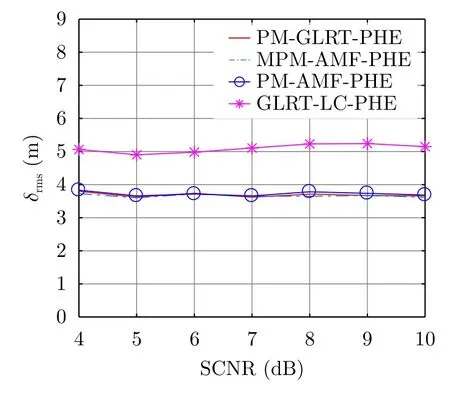
图7 SCNR=18dB时各检测方法的δrms随 γ的变化曲线Fig.7 δrmsagainstγ for each detection method when SCNR=18dB

为说明K的取值对所提出方法的目标检测和距离估计性能的影响，接下来考虑辅助数据数量充足的情况，假设K=2N，其他参数与图3中相同。图8(a)所示，与图3(a)相比，随着K的增大，所有检测方法的Pd均得到提升且性能差距有所减小。在Pd=0.9时，PM-GLRT-PHE相较于MPM-AMF-PHE,PM-AMF-PHE,GLRT-LC-PHE和P-GLRT各存在约0.1dB,0.3dB,2.0dB和3.0dB的性能增益。这表明在辅助数据数量充足时，PM-GLRT-PHE相较于MPM-AMF-PHE与PM-AMF-PHE的性能优势显著减弱，但对于GLRT-LC-PHE和P-GLRT的优势仍然明显。图8(b)给出了相同参数下δrms随SCNR的变化曲线。与图3(b)相比，各检测方法的δrms趋势保持不变，但在相同SCNR下数值均略有降低，这是因为辅助数据数量充足时提高了对ε的估计精度。

图8 辅助数据数量充足时的目标检测和距离估计性能Fig.8 Detection and range estimation performance with sufficient number of auxiliary samples

综上所述，PM-GLRT-PHE作为一种恒虚警检测方法，相比已有的同类型方法有着优良的目标检测和距离估计性能，尤其在辅助数据数量受限的情况下目标检测优势更加明显。此外在不同的部分均匀能量比例因子下，PM-GLRT-PHE均能保持稳健的性能优势，更贴近于实际应用。

5 结束语

本文针对部分均匀干扰环境下的点目标检测问题，提出了一种基于斜对称泄漏模型的GLRT检测方法。考虑到系统采样时存在的目标能量泄漏，采用斜对称泄漏模型对接收信号建模，以弥补泄漏损失的同时减少对辅助数据的需求量，最终联合待检测数据和辅助数据实现所有未知参数的MLE并推导得到PM-GLRT-PHE检测方法。仿真结果表明，所提检测方法不仅具有CFAR特性，而且在辅助数据受限的非理想环境下具有优越的目标检测性能。然而，实际的雷达工作环境复杂多变，杂波往往呈现明显的非平稳性。因此，未来的研究拟将所提出的框架扩展到非高斯混响干扰背景或存在有源干扰的情况。