N2O—C2烃类燃料推进剂燃烧化学反应机理与动力学分析
段志强,郑 东,周 斌
(西南交通大学 机械学院,四川 成都 610031)
0 引言
鉴于肼类推进剂具有优良的燃烧化学特性,被广泛应用于空间化学推进系统,但其也存在显著的缺点:毒性大、腐蚀性强、高致癌性、价格昂贵、操作危险等[1-2]。为满足未来航天技术发展需求,对高性能、低成本、绿色无毒推进系统的研发提出了燃料要求[3]。N2O—C2烃类燃料单元复合推进剂具有性能高、成本低、绿色无毒、适用范围广、宽温幅、推力可深度调节等诸多优势[4-6]。以美国和德国为代表的国外众多研究机构对N2O—C2烃类燃料推进剂体系已开展深入研究[7-8]相比之下国内对与N2O—C2烃类燃料推进剂的研究也正在开展[9-10]。
N2O—C2烃类燃料单元复合推进剂体系其燃料与氧化剂共存,且预混燃烧温度接近3 500 K[11]。不采取防回火措施的情况下,极易发生回火甚至爆炸[12-14]。因此,防回火装置、以及燃烧室结构设计是发动机研制的关键技术问题。其中层流火焰的传播速度对于燃烧室稳定性的设计与评价至关重要[4,15],这就需要对其自点火、火焰传播等基础燃烧特性与化学反应机理进行深入研究,为发动机数值模拟提供准确的燃烧模型。现有文献[16-18]大多以C0—C3反应机理(包含NOx反应机理)作为N2O—C2烃类燃料燃烧反应动力学模型,用于着火延迟时间、火焰传播速度的预测和动力学分析。相对其他推进剂对于N2O—C2烃类体系燃烧反应机理研究较少,Powell等以N2O热解机理和N2O—H2机理为基础,耦合小碳氢反应机理,提出了包含86组分、588个反应的一氧化二氮与小分子烃类的N2O—C1-3化学反应机理,并优化了相关C1—C3的烃类反应的动力学参数[19-20]。
综上所述,N2O—C2烃类燃料燃烧反应机理是预测高能推进剂低温燃烧特性以及发动机数值模拟不可或缺的燃烧模型,然而目前专门针对N2O—C2烃类体系燃烧反应机理研究相对有限。因此,本文首先通过整合N2O和小碳氢燃料反应机理,构建多种烃类燃料一氧化二氮与乙烯、乙炔、乙烷的化学反应动力学模型。然后采用相关文献中的对应实验数据对这些反应机理进行了充分验证,并比较了不同机理预测结果的合理性。进而从反应动力学的角度,深入分析了对不同机理预测结果的差异性。
1 N2O—C2烃类化学反应机理
1.1 机理的发展
正如引言中所述,现有研究大多以包含NOx子机理的碳氢燃料化学反应机理,作为N2O—C2烃类燃料的燃烧反应动力学模型,其机理预测值与实验结果存在不同程度的偏差。这种偏差是否由碳氢燃料或是NOx子机理引起,尚需进一步研究。因此,本文机理发展思路是:以验证充分、应用广泛的小碳氢燃料反应机理为基础,耦合N2O子机理(源于不同NOx机理),以此构建N2O—C2烃类的化学反应动力模型。
鉴于已有的小碳氢燃料的反应机理,国内外已经进行了大量的实验研究并论证了其机理的可行性。其中,GRI 3.0机理[21]、Aramcomech 2.0机理[22]及USC—II机理[23]是目前小碳氢燃料燃烧研究中应用最为广泛的化学反应机理。而且,大量的验证结果表明这些机理在预测C2燃料的着火延迟时间、火焰传播速度、火焰结构等基础燃烧特性较为准确。因此,本文选取GRI 3.0、USC—II以及Aramcomech 2.0机理,作为C2烃类燃料的反应动力学模型。
现有的部分NOx子机理中含有N2O组分以及相关的基元反应,可初步作为N2O子机理。其中,GRI 3.0机理[21]包含N2O相关基元反应,且一定程度上可以预测H2—N2O的层流火焰传播速度。Konnov提出的详细动力学模型[24]中也包含了较为丰富的N2O基元反应,并验证了N2O—Ar体系着火延迟时间和H2—N2O体系层流火焰传播速度。此外,Mével等[25]发展的H2—N2O着火动力学模型,并较为准确预测了H2—N2O—Ar体系的着火延迟时间。因此,本文提取GRI 3.0机理[21]、Konnov机理[24]及Mével机理[25]中的NOx子机理部分,作为N2O子机理。
整合上述C2烃类燃料反应机理和N2O子机理,可获得多种N2O—C2烃类燃料化学反应动力学模型。如表1所示,本文选取了两类具有代表性的动力学模型:一是相同N2O子机理(源于GRI 3.0),不同C2机理,如GRI 3.0、USC-GRI和Aram-GRI;二是相同C2机理(源于USC—II)、不同N2O子机理,如USC-GRI、USC-Konnov和USC-Mével。针对反应机理的实验验证以及不同机理预测结果的对比分析将在下一节论述。

表1 N2O—C2烃类燃料化学反应动力学模型
1.2 机理的验证
依据现有文献的反应机理与对应的实验数据,本文将从N2O—C2烃类燃料体系的层流火焰传播速度和着火延迟时间等两个方面对上述反应机理的准确性进行验证。化学反应动力学的数值计算在CHEMKIN程序上完成,其实验条件与文献[16]中的给定条件保持一致。
1.2.1 着火延迟时间
Mével等采用激波管台架,测量了初始压力0.32 MPa、初始温度1 399~1 862 K,0.549%C2H2/3.447%N2O/96.004%Ar和0.4%C2H6/3.598%N2O/96.002% Ar(摩尔分数)体系的着火延迟时间[16]。图1分别给出了相同N2O子机理、不同C2机理以及不同N2O子机理、相同C2机理的反应动力学模型预测的着火延迟时间,并与对比了R.Mével的实验结果数据[16]。
由图1可见,采用GRI 3.0的N2O子机理的反应动力学模型(如GRI 3.0、USC-GRI和Aram-GRI)预测结果均偏高,而采用Konnov[24]和Mével[25]的N2O子机理的反应动力学模型(如USC-Konnov和USC-Mével)预测结果与实验结果基本吻合。
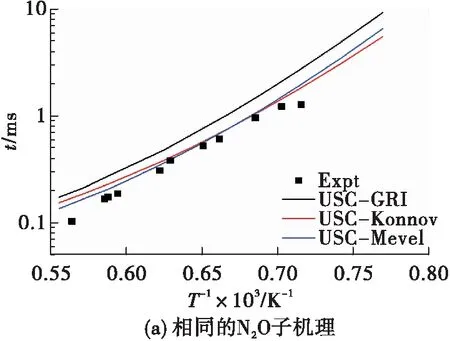
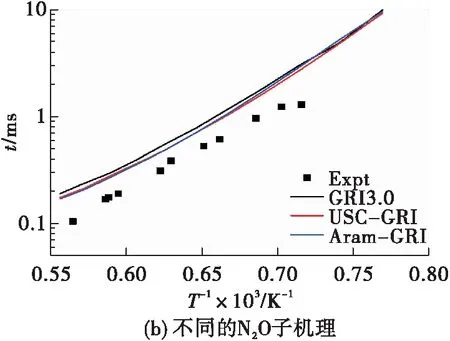
图1 N2O—C2H2—Ar着火延迟时间实验值与预测值Fig.1 Predicted and experimental results for N2O—C2H2—Ar ignition delay time
综合对比图1,不难发现,相同N2O子机理的反应动力学模型预测的着火延迟时间基本一致,而不同N2O子机理的反应动力学模型预测的着火延迟时间存在较大偏差。这说明了C2机理对N2O—C2H2—Ar的着火延迟时间影响较小,而N2O子机理却对其有显著影响。与之类似的结论也体现于N2O—C2H6—Ar燃烧体系(见图2)[11]。

图2 N2O—C2H6—Ar着火延迟时间实验值与预测值Fig.2 Predicted and experimental results for C2H6 ignition delay time
图3给出了初始压力0.4 MPa、初始温度1 150~1 700 K、化学计量比1.0,上述两类N2O—C2反应动力学模型所预测的N2O—C2H4—N2体系着火延迟时间与Deng等的激波管实验结果的对比[18]。由图4可见,总体而言两类N2O—C2反应动力学模型均能较好预测N2O—C2H4—Ar着火延迟时间,其中USC-Konnov模型预测的准确度最高。综合对比图3中(a)和(b)同样可见,C2机理对N2O—C2H4—Ar的着火延迟时间影响较小,而N2O子机理却对其有较大影响[17]。与之相似的结论也体现于N2O—C2H4—Ar(化学计量比2.0)富燃工况(见图4)[18]。

图3 N2O—C2H4—N2(φ=1.0)着火延迟时间实验值与预测值[12]Fig.3 Predicted and experimental results for C2H4— N2O—N2 (φ=1.0) ignition delay time
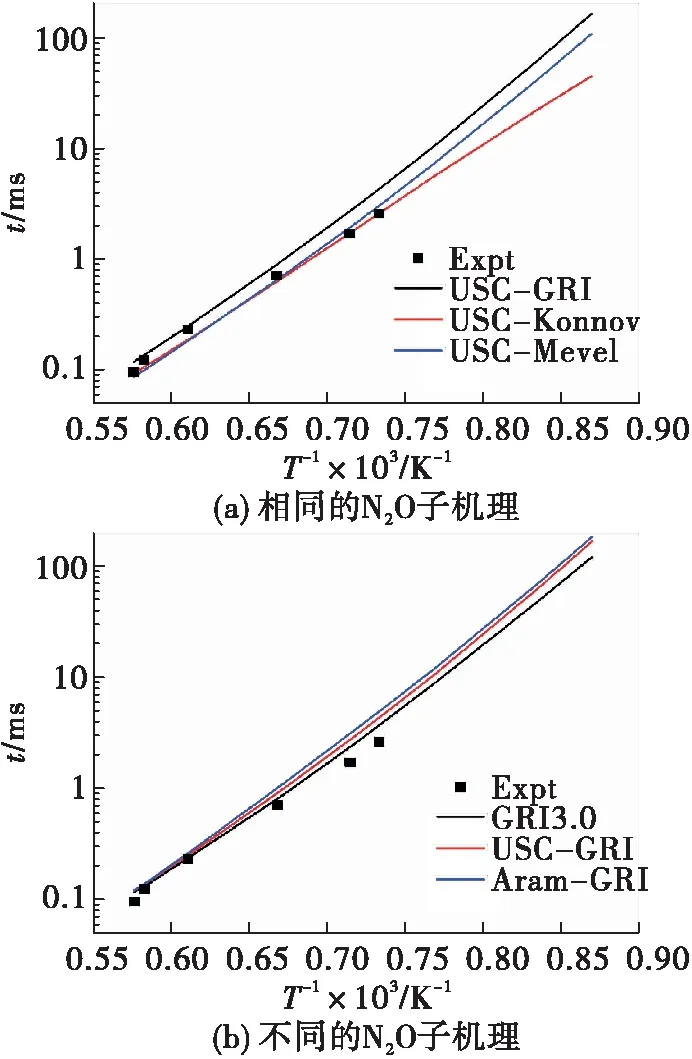
图4 N2O—C2H4—N2(φ=2.0)着火延迟时间实验值与预测值Fig.4 Predicted and experimental results for C2H4— N2O—N2 (φ=2.0) ignition delay time
1.2.2 层流火焰传播速度
Powell等在层流火焰传播速度测量中用平面火焰热流法,在初始温度298 K、化学计量比0.56~1.6、压力0.08 MPa,进行测量N2O—C2H2—N2体系的绝热层流火焰的传播速度[20]。图5分别给出了两类N2O—C2反应动力学模型预测的层流火焰传播速度,通过实验结果[20]比较如下。由图5可见,GRI3.0和USC-GRI模型预测值偏低,USC-Konnov模型预测值与实验测量值最为接近。对比图5不难发现,C2机理仅在富燃工况下对N2O—C2H2—N2层流火焰的传播速度有一定影响,而N2O子机理在整个化学计量比范围内对其均有较大影响。

图5 N2O—C2H2—N2层流火焰传播速度预测值与实验值Fig.5 Predicted and experimental results for N2O—C2H2—N2 laminar flame velocity
Naumann等采用与平面火焰热流法不同的本生灯火焰方法,在初始温度473 K、化学计量比0.6~2.0,压力0.1 MPa和0.3 MPa,测量N2O—C2H4—N2体系的层流火焰传播速度[17]。图6中为两类N2O—C2反应动力学模型预测的层流火焰传播速度与实验结果的对比,可见两类N2O—C2反应动力学模型的预测值均远低于实验值。对比图6同样可以发现,对于N2O—C2H4—N2层流火焰传播速度而言,C2机理仅在富燃工况下有一定影响,而N2O子机理在整个化学计量比范围内均有较大影响。

图6 N2O—C2H4—N2层流火焰传播速度预测值与实验值Fig.6 Predicted and experimental results for N2O—C2H4—N2 laminar flame velocity
综上验证与对比分析表明:对N2O—C2烃类燃料的着火延迟时间而言,C2机理影响较小,而N2O子机理却有显著影响。对其层流火焰传播速度而言,C2机理仅在富燃工况下有一定影响,而N2O子机理在整个化学计量比范围内均有较大影响。为此,本文将在下一节中从反应动力学的角度进行深入系统的分析研究,通过CHEMKIN1进行灵敏性分析和给出一个合理的解释。
2 动力学分析
针对N2O—C2H4—N2体系,分别进行着火时刻的温度灵敏度分析和火焰传播速度灵敏度分析,并取灵敏度系数绝对值最大(即对着火、燃烧过程影响较大)的前10个基元反应。灵敏度分析计算通过上述化学反应动力学软件进行分析,并选择GRI 3.0、USC-GRI和USC-Konnov反应动力学模型。
2.1 温度灵敏度分析
图7~图9分别给出了初始温度1 000 K和1 500 K、压力0.4 MPa、化学计量比1.0条件下,由GRI 3.0、USC-GRI和USC-Konnov反应动力学模型计算的N2O—C2H4—N2体系温度灵敏度分析结果。

图7 GRI 3.0温度灵敏度分析系数Fig.7 Sensitivity coefficients of temperature using GRI 3.0 model

图8 USC-GRI温度灵敏度分析系数Fig.8 Sensitivity coefficients of temperature using USC-GRI model
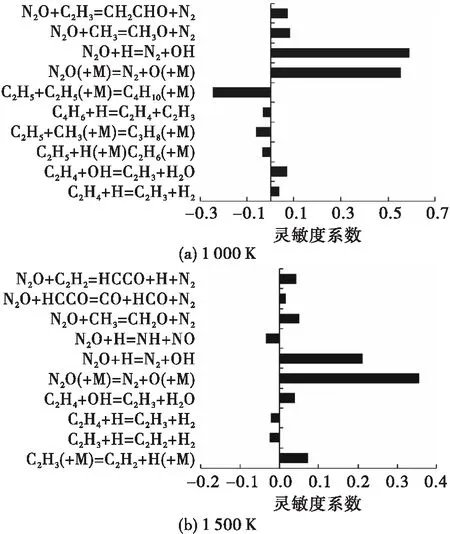
图9 USC-Konnov温度灵敏度分析系数Fig.9 Sensitivity coefficients of temperature using USC-Konnov model
由图7~图9可以看出下面两个基元反应对化这反应动力学模型影响最大。
N2O+M=N2+O+M
(1)
N2O+H=N2+OH
(2)
基元反应式(1)和式(2)的温度灵敏度系数最高,对N2O—C2烃类燃料的着火过程起决定性的作用。其中式(1)为N2O初始裂解反应,生成N2和重要的O自由基,决定了燃烧系统的氧化进程。式(2)为N2O与H自由基反应,是重要的放热反应,对着火过程系统温升起关键性作用。而反应中OH自由基浓度是着火时刻的重要判据,上述反应的作用是促进生成高活性OH自由基和促进N2的链传递反应。
对比图7和图8可见,对于相同N2O子机理、不同C2机理GRI 3.0和USC-GRI反应动力学模型而言,其温度灵敏度分析结果基本一致。除了N2O相关反应式(1)和式(2)外,其他均是碳氢相关反应,且温度灵敏度系数相对较低。因此,GRI 3.0和USC-GRI预测的着火延迟时间基本一致。
对比图8和图9可见,对于相同C2机理、不同N2O子机理的USC-GRI和USC-Konnov反应动力学模型而言,其温度灵敏度分析结果却有较大差异。对于USC-Konnov模型除了反应式(1)和式(2)外,还有一些N2O氧化碳氢组分(如CH3、C2H2、C2H3等)的反应也具有一定的温度灵敏度系数。因此,USC-GRI和USC-Konnov预测的着火延迟时间差距较大。
上述动力学分析表明:对N2O—C2烃类燃料的着火延迟时间而言,C2机理影响较小,而N2O子机理却有显著影响,其中基元反应(1)和(2)对N2O—C2烃类燃料的着火过程起决定性的作用。
2.2 火焰传播速度灵敏度分析
图10~图12分别给出了初始温度473 K、压力0.1 MPa、化学计量比0.6和2.0条件下,由GRI 3.0、USC-GRI和USC-Konnov反应动力学模型计算的N2O—C2H4—N2体系火焰传播速度灵敏度分析结果。由图10(a)、图11(a)和图12(a)可见,贫燃料工况时灵敏度分析的反应几乎全部体现在N2O子机理。其中,基元反应式(1)的灵敏度系数最高,对层流火焰传播速度起主导作用。
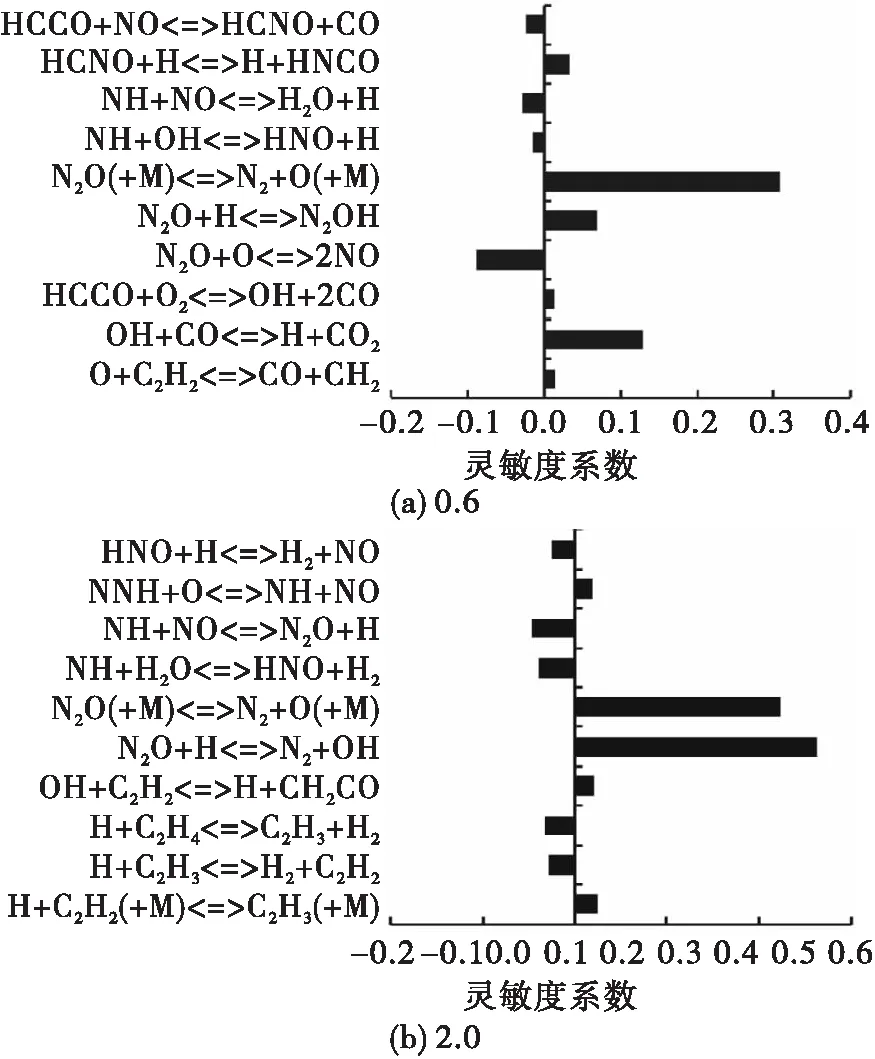
图10 GRI 3.0层流火焰传播速度灵敏度分析系数Fig.10 Sensitivity coefficients of laminar flame velocity using GRI 3.0 model
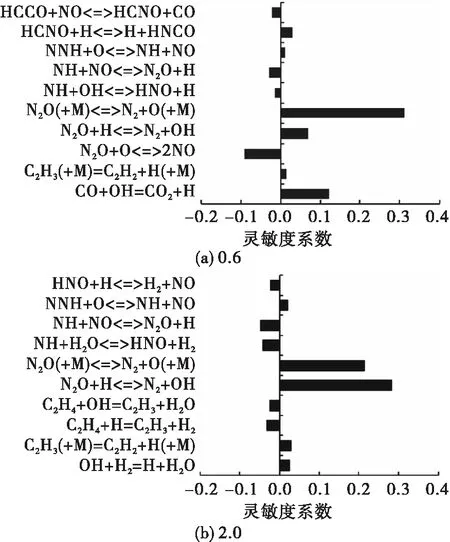
图11 USC-GRI层流火焰传播速度灵敏度分析系数Fig.11 Sensitivity coefficients of laminar flame velocity using USC-GRI model

图12 USC-Konnov层流火焰传播速度灵敏度分析系数Fig.12 Sensitivity coefficients of laminar flame velocity using USC-Konnov model
N2O+O=NO+NO
(3)
CO+OH=CO2+H
(4)
反应式(2)~式(4)也具有较高的灵敏度系数。其中,反应式(3)为负影响,这是由于反应式(3)消耗氧化剂N2O,同时还消耗了重要的O自由基,并生成稳定组分NO。反应式(4)为正影响,不仅生成能促进火焰传播的H自由基,而且CO被氧化为CO2时放出大量热量[26]。
而由图10(b)、图11(b)和图12(b)可见,富燃料工况时基元反应式(2)的灵敏度系数最高,式(1)和式(2)共同对层流火焰传播速度起主导作用。且除N2O子机理相关基元反应外,C2机理部分反应也有一定的灵敏度系数,并对火焰传播速度产生一定的影响。主要表现为C2组分脱氢反应(自由基攫氢、裂解脱氢),其中消耗H自由基的反应灵敏度系数为负值,生成H自由基的反应灵敏度系数为正。
上述动力学分析表明:对N2O—C2烃类燃料的火焰传播速度而言,C2机理仅在富燃工况下有一定影响,而N2O子机理在整个化学计量比范围内均有较大影响。贫燃料工况时基元反应(1)的灵敏度系数最高,而富燃料工况时式(2)的灵敏度系数最高。
3 结论
本文以验证充分、应用广泛的小碳氢燃料反应机理为基础,耦合N2O子机理(源于不同NOx机理),进而构建了多种N2O—C2烃类燃料燃烧化学反应动力学模型。其中,USC-Konnov模型能更为准确地预测N2O—C2体系着火延迟时间以及N2O—C2H2体系层流火焰传播速度,为进一步发展NOFBX燃烧反应机理奠定基础。
预测结果的对比分析表明:对N2O—C2烃类燃料的着火延迟时间而言,C2机理影响较小,而N2O子机理却有显著影响。对其层流火焰传播速度而言,C2机理仅在富燃工况下有一定影响,而N2O子机理在整个化学计量比范围内均有较大影响。
通过灵敏度分析确定了对N2O—C2烃类燃料着火延迟时间、火焰传播速度影响较大基元反应,并解释上述结论。其中,基元反应N2O+M=N2+O+M和N2O+H=N2+OH对N2O—C2烃类燃料体系的着火、燃烧过程起着决定性作用。

