基于UKF与EKF算法的配电网状态估计
张叶贵,徐登国,李大巧
(六盘水师范学院,贵州六盘水,553000)
0 引言
在我国的电力建设初期,由于资金较为匮乏,其电力系统的建设较为偏重对电力系统运行更为重要的输点网中,对配电网的重视程度还不够[1]。加之配电网节点数众多,若对配电网中每个节点都安装量测装置会造成资源的极大浪费[2],因此,对未配置量测装置的节点只能通过状态估计算法进行预测[3]。精确的系统状态估计模型是提升状态估计精度的基础,状态方程的建立是依据历史状态变量数据变化规律建立的,它反应的是系统状态量随时间变化的规律。因此,如何建立最为接近系统真实的动态状态模型是状态估计的关键。系统的动态状态模型误差越小,预测出的系统状态量就越接近于真值。
由于卡尔曼滤波在实际应用中受到限制,即要求系统为线性系统。实际情况下大多数系统为非线性系统,EKF算法就是为了解决非线性系统状态估计问题而被提出。本文将UKF算法与EKF算法引入到配电网进行状态估计,并考虑到分布式能源接入配电网的情况进行仿真分析,采用潮流计算结果作为真值,在真值的基础上添加量测误差作为量测数据,采用IEEE13节点标准算例对两种算法进行对比分析。
1 EKF与UKF算法
采用1式表示状态估计的状态方程与量测方程

上式中,x为状态方程中的状态向量,z为量测方程,w、v分别表示输入噪声与观测噪声,k表示时间。EKF算法流程参见文献[4],UKF算法流程如下所示:
1)状态量预测

2)量测量预测
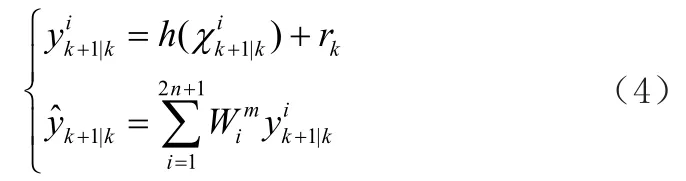
该时刻的量测预测值。
3)滤波修正
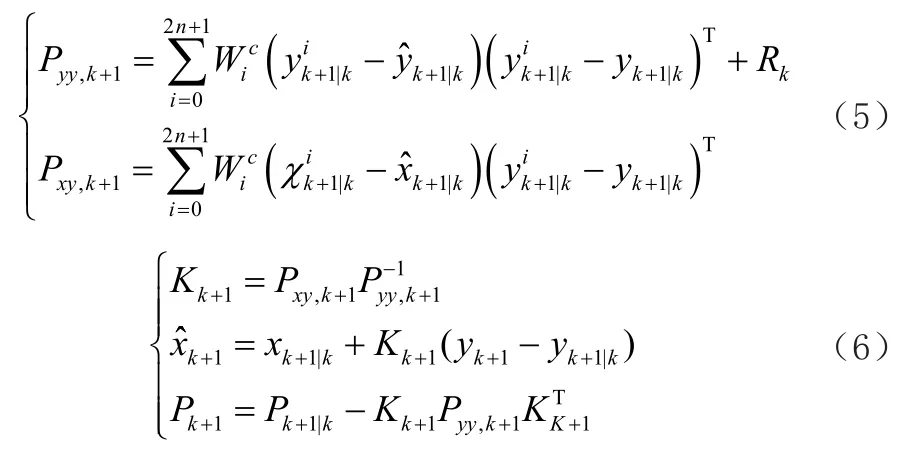
至此完成UKF滤波过程。
2 仿真分析
本文采用IEEE13节点标准算例进行仿真分析,如图1所示。对于仿真过程中的初始噪声方差阵Q0中的主对角元素取值为10-6,非对角线元素取值为零;初始协方差阵P0中的主对角线元素取值为10-6,非对角线元素取值为零。通过潮流计算结果作为真值,量测数据在潮流真值的的基础上添加高斯白噪声所得。由UKF算法的计算步骤可知,在sigma采样与权值计算过程中需要确定三个参数,其参数取值为:a=10-3、、κ=0、b=2;此外对于UKF算法中的状态转移函数f(·)由两参数指数平滑法获取,其中对应的参数取值为:p=0.85,q=0.05。对于IEEE13节点系统进行仿真分析时,对系统采样每五分钟进行一次,一天中共采样288次。以SCADA量测系统误差为例,取功率量测误差、电压相角量测的均值为0,标准差为0.02;电压幅值的量测误差的均值为0,标准差为0.01。
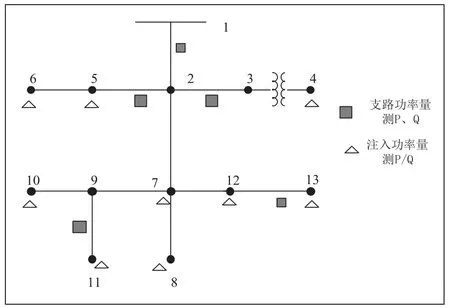
图1 IEEE33节点接线图
为量化两种算法的性能指标,采用电压幅值的平均相对误差无电压相角的平均绝对误差来标准算法的性能指标,其表达式如下:
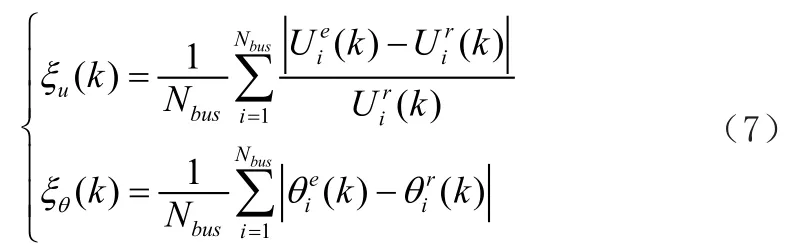
上式中的上标e表示预测值,r表示真值。对系统进行采样分析,采样次数为288次,下图为两种算法的电压幅值与电压相角以及真值的结果对比图。
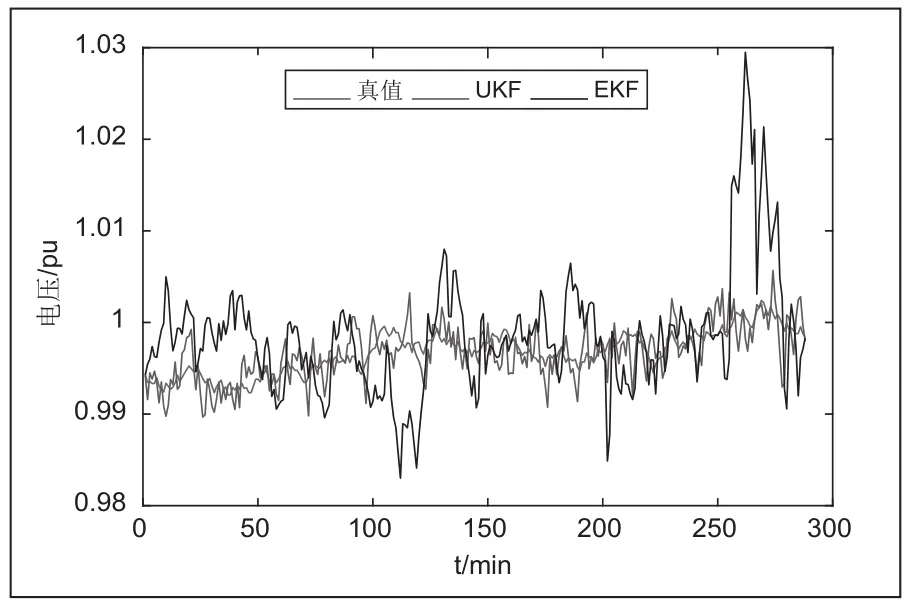
图2 电压幅值滤波结果对比

图3 电压相角值滤波结果对比
下表为两种算法的电压幅值的平均相对误差无电压相角的平均绝对误差滤波结果对比。
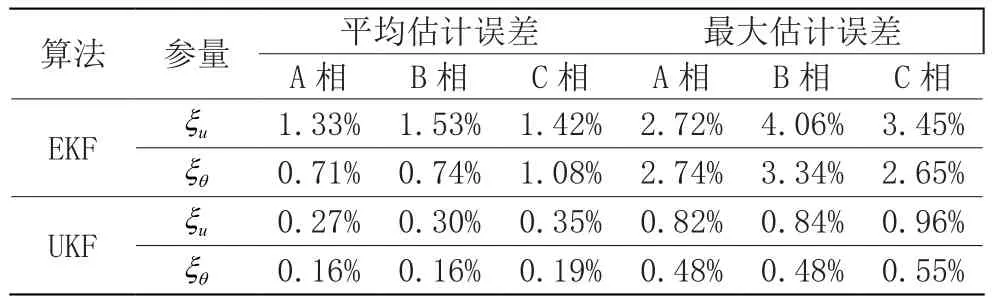
表1 系统正常运行时状态估计指标
由表中数据可知,UKF算法无论是电压性能指标还是相角性能指标都要优于EKF算法,仿真中对系统进行采样次数为288次,EKF是算法时长为42秒,UKF算法的计算时长为38秒。而SCADA系统的采样周期一般为2秒。因此两种算法的皆满足系统要求。
3 结论
本文采用EKF算法与UKF算对配电网进行状态估计,通过仿真分析验证了两种算法皆能满足系统性能指标,通过对两种算法仿真结果进行对比分析,得出了UKF算法性能指标要明显优于EKF算法,UKF算法具有更好的滤波跟踪性能以及更好的鲁棒性。
在配电网向智能化发展的今天,配电网中存在多种量测数据如AMI智能电表量测数据、微型量测单元(μPMU)、SCADA量测多种量测数据融合,配电网量测数据呈指数型增长,如何充分利用配电网中的多种量测数据以提升状态估计精度仍需进一步研究。

