解析法及数值法在求解压力容器缺陷应力强度因子中的应用 ①

□□ 张巨银，王文达，王学平，牟龙龙，赵志琦

(1.甘肃省特种设备检验检测研究院，甘肃 兰州 730050；2.宁夏特种设备检验检测院，宁夏 银川 750000)

引言

GB/T 19624—2019《在用含缺陷压力容器安全评定》[1]于2020年1月1日正式颁布实施。该标准以裂纹张开位移和应力强度因子为主要参量，以弹塑性双判据法为基础，对压力容器缺陷进行安全评定。

应力强度因子为表征裂纹尖端应力场强度的物理量，是含缺陷压力容器安全评定的重要内容，其求解方式主要有解析法和数值法。GB/T 19624—2019中详细地区分了压力容器的缺陷类型，并规定了各种缺陷的安全评估方法，同时也加入了更多缺陷评估中间参量的计算模型和方法。在平面缺陷的评估中，明确地指出了多种情况下的应力强度因子计算模型，评定人员可以根据相应的模型来便捷地计算相应的工程问题。

尽管目前标准中的计算模型可以覆盖部分常见工程结构，但对于一些较为特殊的问题还是无从下手，而利用XFEM技术计算裂纹尖端应力强度因子则具有更好的适应性。XFEM技术可以快速准确地建立含缺陷结构的有限元计算模型。

本文以平板裂纹模型为例，分别采用GB/T 19624—2019中的解析法和XFEM数值法对相同工况下裂纹尖端的应力强度因子进行求解，并对两种方法所得计算结果的差异性进行对比分析。

1 XFEM技术的介绍

扩展有限元法(XFEM)自Belytschko T等[2]首次提出以来，在断裂力学领域的研究中得到了一定程度的普及与发展。ZHUANG Z等[3]基于XFEM计算出的数值结果与实验数据进行比较，证明了XFEM计算的准确性及效率；郭历伦等[4]对制约扩展有限元发展的两个问题及其修正方法进行了讨论；陈华等[5]基于XFEM计算了裂尖应力变化及裂纹扩展期间的能量变化，体现了扩展有限元法的准确性以及其在裂纹扩展领域得天独厚的优势，为工程实际应用提供参考。

扩展有限元法的基本思路是利用不同的单元位移模型来对裂纹路径上单元的位移不连续性进行描述。根据与裂纹扩展路径的位置关系，有限元模型中的单元类型被划分为三种：常规单元、裂纹贯穿单元以及裂纹处单元，如图1所示。

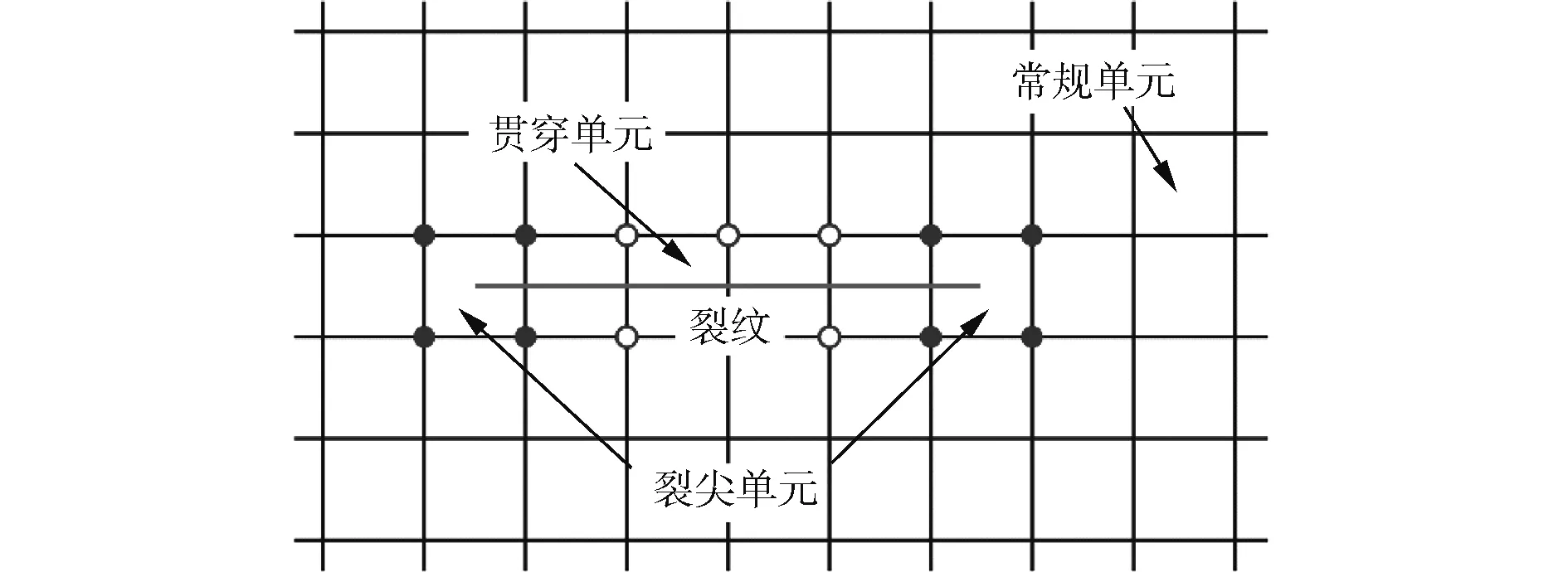
图1 数值模型单元示意图

三种单元的位移模式见式(1)～(3)。

ui(x)=∑Niui

(1)

uj(x)=∑(Niui+NjH(x)uj)

(2)

uk(x)=∑(Niui+NkφSuk)

(3)

式中，i、j、k分别对应常规单元、裂纹贯穿单元以及裂纹处单元，Ni、Nj和Nk分别为三种单元的位移形函数，ui、uj以及uk为相应单元的节点位移。H(x)与φS为Heaviside函数与裂尖增强函数，分别用于描述裂纹面与裂纹尖端的不连续性，具体见式(4)和(5)。

式中，r与θ为以裂纹尖端的原点的极坐标系坐标值。

通常，XFEM中裂纹尖端的应力强度因子会采用相互作用积分法来计算，其求解的相应过程在文献[6-7]中有较为详细的说明，这里就不再赘述。本文的数值计算过程在ALOF软件中进行，它是基于XFEM技术开发的国产有限元软件，可以快速计算复杂三维模型上裂纹的应力强度因子，在一些工程案例中得到了良好的应用。

2 解析解计算模型

GB/T19624—2019《在用含缺陷压力容器安全评定》提供了常见含缺陷结构缺陷尖端部位的应力强度因子K的计算公式，在此主要介绍标准中平板(板宽2W，板长2L，板厚B)表面裂纹和埋藏裂纹的应力强度因子求解的计算模型。

GB/T19624规定在计算应力强度因子时，所取用的应力是缺陷部位的主应力，计算该主应力时采用线弹性计算方法，并假设结构中不存在缺陷。沿板厚方向利用应力线性化规则计算薄膜应力σm与弯曲应力σB，计算方法见式(6)和式(7)。

式中，σ1、σ2可分别取模型厚度方向两个表面的第一主应力。

裂纹尖端的应力强度因子表达式见式(8)。

式中，a为裂纹半长，fm、fb分别为裂纹构形因子。

对于半椭圆表面裂纹，其构形因子计算见式(9)～(12)。

(9)

式中，c为裂纹深度，B为平板厚度，上标A与B分别为裂纹深度处K的裂纹构形因子与裂纹长度方向两端处K的裂纹构形因子。

对于椭圆埋藏裂纹，其构形因子计算见式(13)～(16)。

(14)

(15)

(16)

式中，c为裂纹高度的一半，B为平板厚度，上标A与B分别为裂纹深度处K的裂纹构形因子与裂纹长度方向两端处K的裂纹构形因子。

3 解析解模型与结果

依据GB/T19624的计算模型来计算平板上表面裂纹的应力强度因子。在通用有限元软件中建立如图2所示的正方体平板模型，其中，L=160mm，B=30mm，左端为固定边界，右端施加140MPa的拉力。材料弹性模量取210 000MPa，泊松比取0.3。

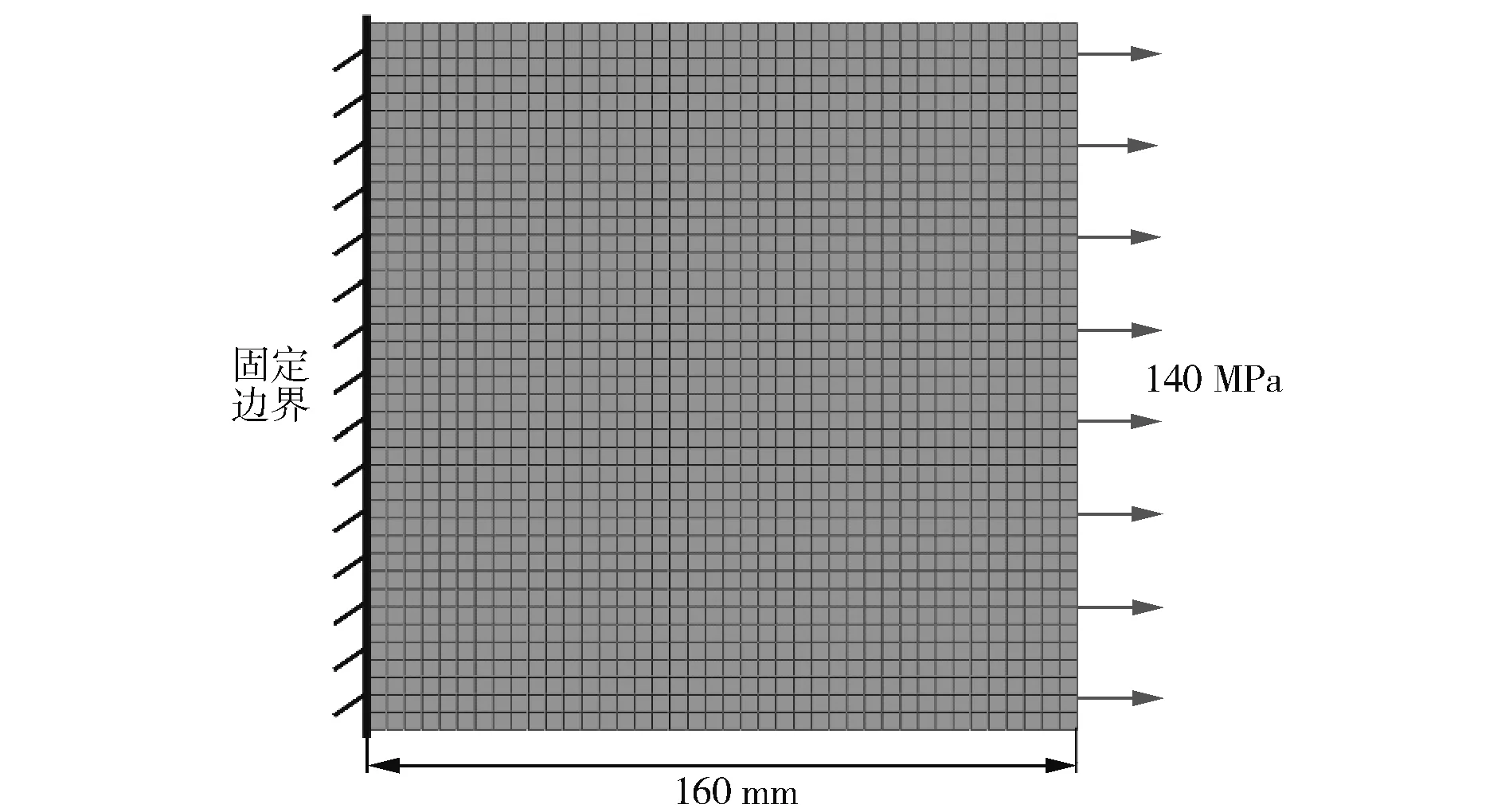
图2 数值模型

在计算完成后，沿板厚方向取上下两个面的第一主应力σ1、σ2，其值均为143MPa，进一步根据应力线性化规则和公式(6)、(7)计算得到σm与σB，分别为143MPa与0。

平板上的裂纹的尺寸见表1。

表1 裂纹尺寸 mm

将以上数据代入标准第二部分的计算公式中即可计算得到裂纹的K1值，计算结果见表2。

表2 解析解计算结果 N/mm3/2

4 数值解模型与结果

采用XFEM技术实现平板裂纹的应力强度因子数值法求解，主要步骤如下：

(1)建立正方形平板数值模型，其尺寸和受力状况均与上文解析法求解部分所建立的模型保持一致。

(2)建立一个半椭圆平面型裂纹，裂纹的短半轴长度为5mm，长半轴长度为8mm。采用三角形网格对其进行离散。

(3)建立一个椭圆埋藏型裂纹，裂纹的短半轴长度为2.5mm，长半轴长度为8mm。采用三角形网格对其进行离散。

(4)分别将平板模型和两种裂纹模型进行耦合，形成含缺陷模型。图3为耦合得到的含半椭圆裂纹缺陷平板的数值模型；图4为表面裂纹和埋藏裂纹分别在平板模型壁厚方向所处状态的局部视图。

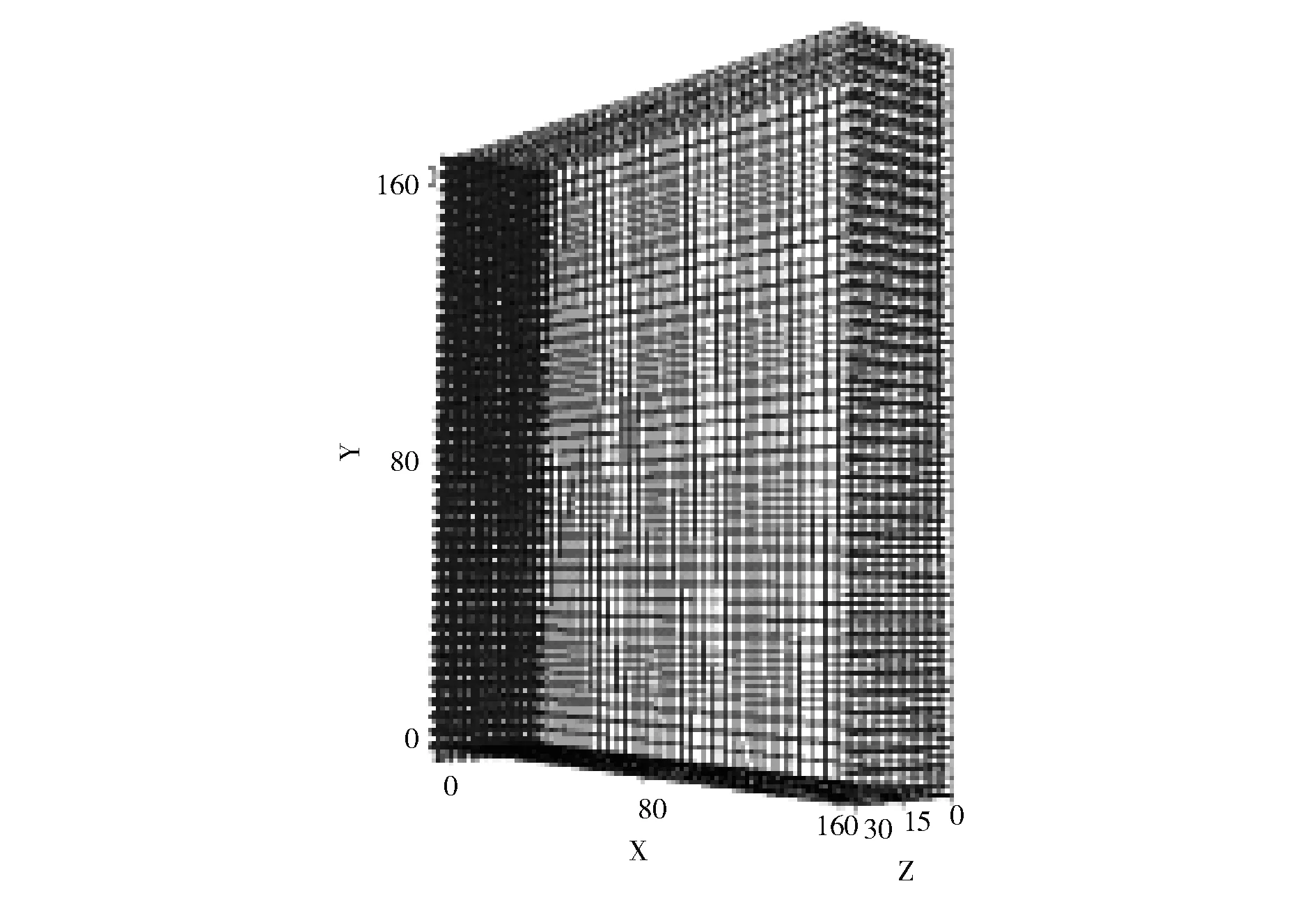
图3 含半椭圆裂纹缺陷的平板模型

图4 裂纹在平板壁厚方向所处位置的示意图

(5)完成计算，直接输出应力强度因子值。表面裂纹最大应力强度因子计算结果为：KI=451.16N/mm3/2。埋藏裂纹最大应力强度因子计算结果为：KI=326.54N/mm3/2。

表3为解析计算结果与XFEM数值计算结果的对比，可以看出两种方法计算结果的最大相对误差在10%左右，数值法结果普遍小于解析法结果。同时，数值法结果更加求准，解析法结果更加保守，更有利于保证含缺陷承压设备的安全使用。当然XFEM数值法在计算含缺陷压力容器的应力强度因子中也具有较好的适用性。

表3 规范计算结果与数值解最大值对比

5 结论

5.1GB/T19624—2019中解析解计算流程明确，算法直接，但其所用公式复杂，并且需要借助有限元软件对模型前期的受力状态进行求解。

5.2XFEM技术对求解应力强度因子有良好适应性，其建模简单，计算结果输出方便，需要使用者掌握一定的有限元基础知识。

5.3 两种方法计算平板表面裂纹模型应力强度因子结果的相对误差在10%左右，可以达到工程计算精度要求，应视具体情况选用合适的方法进行计算。