低轨卫星宽带OFDM通信相位噪声群时延的联合估计 *

张 毅

(中国西南电子技术研究所,成都 610036)

0 引 言

正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术[1]被广泛应用于当前众多的地面通信系统空口标准中。由于其在频谱效率和可靠性等方面的众多优势[2]，如今已成为地面通信系统中举足轻重的标志性传输技术之一。

低轨卫星通信系统具有广覆盖、低延迟、高可靠的特点，是地面通信系统的有益补充与增强。在空天地海一体化网络融合发展的大趋势下，采用OFDM技术作为低轨卫星通信系统的基础传输技术已成为研究热点[3]。同时，为适应当前无线数据流量的爆发式增长，低轨卫星宽带通信系统的工作频段正朝向Ka、Q、V等高频段发展，信号带宽达到数百兆赫。

低轨卫星宽带OFDM通信系统作为在高频段范围内工作的系统，使用的“总”振荡器(包括参考时钟、环路滤波器和其他锁相环组件)的相位噪声电平将显著高于传统通信系统，影响系统容量。同时，宽带信号经过系统传输路径和线性元件时，其各个频率分量的响应不同、系统群时延不再为常数也将导致相位失真。因此，有必要对低轨卫星宽带OFDM通信系统中相位噪声和群时延的估计与补偿方法进行研究，以提升系统性能。

目前，对于相位噪声和群时延单独估计和补偿的方法已被广泛研究[4-11]。对于系统中群时延的影响，文献[8]采用无限脉冲响应(Infinite Impulse Response，IIR)滤波器来补偿系统中非线性群时延相位带来的影响,文献[9]指出通过泰勒级数能够有效地建模群时延的非线性特性,文献[10]基于这种建模方法研究了群时延对于OFDM系统的影响，文献[11]采用傅里叶分解的办法准确地拟合了群时延特性。

上述研究仅仅考虑群时延和相位噪声的独立估计与补偿，然而在实际的低轨卫星宽带OFDM系统中相位噪声和群时延影响同时存在于系统中，共同导致传输信号的相位扭曲，两者产生的相位失真效应相互耦合，单独分离的处理过程不可避免地存在性能损失。因此，本文提出了一种相位噪声群时延联合估计算法。首先对相位噪声群时延因素耦合下接收信号特征进行了理论分析，然后利用群时延泰勒级数展开模型推导了基于导频的群时延频域估计方法，并对完成群时延影响消解后的导频相位估计值进行时域内插得到相位噪声估计值，最后得到所有时频域符号的公共相位误差估计值。

1 OFDM系统模型

1.1 系统模型

在低轨卫星宽带OFDM系统中，信号经过OFDM调制到达接收机的过程中会受到相位噪声、群时延和高斯噪声的影响。其中相位噪声通常由发射机中上变频到载波频率的有源器件和有损器件引入，工作频段越高影响越大；而群时延主要由不同频率分量经过媒质传输路径或系统中的线性器件产生，信号带宽越宽影响越大。在低轨卫星宽带OFDM系统中，这两项因素均不可忽略。

图1所示为考虑相位噪声和群时延后的低轨卫星宽带OFDM系统模型，包括串并变换、循环前缀(Cyclic Prefix，CP)、快速傅里叶变换(Fast Fourier Transform，FFT)、逆快速傅里叶变换(Inverse Fast Fourier Transform，IFFT)、相噪群时延联合估计算法等几个部分。

图1 低轨卫星宽带OFDM系统相噪群时延联合估计模型图

不失一般性，本文假设在相位噪声产生前后系统引入的群时延影响分别表示为τ1(k)和τ2(k)。

假设OFDM系统共有N个子载波，采样后离散的OFDM符号时域表示为y(n)，不同时刻的相位噪声为θ(n)，则经历第一级群时延和相位噪声影响后的OFDM时域基带信号可以表示为

(1)

式中：n=0,1,…,N-1；Xk为第k个子载波上的发送符号；g1(k)=ejφ1(k)为第一部分群时延干扰在第k个频点的频域响应，其相位角的连续函数φ1(ω)与群时延之间关系可以写作

(2)

同理，第二部分群时延的频域响应可以写作g2(k)=ejφ2(k)，最终受到相位噪声和两部分群时延影响后解调得到的OFDM符号为

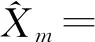
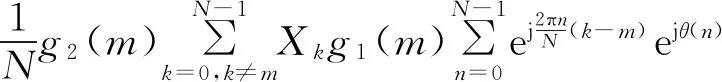
(3)

式中：m=0,1,…,N-1。

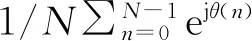
因此在相位噪声和群时延耦合作用下，系统接收OFDM符号受到的影响可以分为ICI和CPE两部分，其中CPE的影响只与系统总群时延效应和平均相位噪声有关。

1.2 群时延模型

群时延导致的相位失真以频率分量之间的时延差值来衡量。传统的建模方法并不能反映出相位的非线性度[9]，为了能够有效建模系统群时延响应，本文采用泰勒级数分离出系统中的线性相位和不同程度的非线性失真相位，以建模系统中群时延的影响。

将系统的相位表示为中心频率ωc附近不同次数的形式：

φ(ω)=a0+a1(ω-ωc)+a2(ω-ωc)2+a3(ω-ωc)3+… 。

(4)

其中：

(5)

根据定义，群时延可以表示为

-a1-2a2(ω-ωc)-3a3(ω-ωc)2+…≜

-b1-b2(ω-ωc)-b3(ω-ωc)2+…。

(6)

式中:b0为线性相位成分，定义为零阶群时延系数；b1包含二次相位成分，定义为一阶群时延系数；依此类推。

2 相噪群时延联合估计算法

根据前述相噪群时延联合影响表达式和群时延泰勒级数展开模型，本节设计了一种相噪群时延联合估计算法。

2.1 导频图样

为达到较好的估计性能，OFDM系统一般基于导频符号的导频子载波进行信号估计，这里参考5G NR的PTRS设计，在时频域分别插入导频子载波，以估计不同子载波和不同时隙处的公共相位误差。在导频设计时，相位跟踪的准确度和导频开销存在一定的取舍。当导频的密度越大时，相位跟踪的准确度越高，能够更好地估计CPE，但是也会导致传输信号的浪费。图2给出了一种导频图样示意，其中前两个符号为物理下行控制信道(Physical Downlink Control Channel，PDCCH)子载波。

图2 导频图样示意

假设单个时隙内时域共有N个OFDM符号，频域共有M个子载波，总的数据矩阵为X∈CM×N。导频在时域的符号间隔为K-1个，在频域的子载波间隔为L-1个，则发送数据可以表示为

X(m,n)=X(aL+l,bK+k)=

(7)

式中：L=M/Na，K=N/Nb,Na和Nb分别代表子载波上的导频个数和时域的导频个数;inf.data表示插入的数据符号。

2.2 二维联合估计算法设计

根据公式(3)中第一部分公共相位误差的表达形式，采用最小二乘(Least Square,LS)估计，可以计算出导频信号的公共相位误差：

(8)

式中：C(a,b)表示第b个导频符号第a个导频子载波的CPE估计值，对应矩阵表示为Cp；Y(a,b)和X(a,b)分别表示第b个导频符号第a个导频子载波位置的接收信号和发送导频信号，对应矩阵表示为Yp和Xp；g(a)为第a个导频子载波的群时延响应；θb(n)为第b个导频时隙的相位噪声。

从式(8)中可以看出,CPE可以分为两部分：第一部分g(a)为总的群时延影响，只与频域子载波参数有关;第二部分为某一OFDM符号时间内所有相位噪声的平均值，只与时间有关，与频率无关。

2.2.1 频域群时延估计

由于同一个OFDM符号不同子载波的相位噪声为一常数，可以视作叠加了一个恒定相位。而且对于不同符号同一子载波的群时延特性是相同的，可以进行时隙内联合处理以平滑噪声。同时，综合考虑估计精度和复杂度，这里选定群时延泰勒展开的级数为4。因此，将公式(4)、(8)简化后可以得到如下群时延相位表达式：

φp=Wpα。

(9)

其中：

(10)

(11)

(12)

进一步可以将群时延估计问题转化为最优化问题：

(13)

该问题在LS准则下能够求得最优解：

(14)

2.2.2 时域相位噪声估计

时域的相位噪声可以通过线性内插的方法进行估计[12]，首先消除CPE中群时延失真的部分，得到不同OFDM导频符号处的相位噪声：

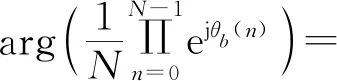
(15)

具体的算法步骤总结如下：

输入参数W、Y、X。

Step1 群时延系数估计：

(1)根据公式(8)计算所有导频子载波的CPE频域响应Cp；

(2)根据公式(10)计算经过时隙内平滑后的平均CPE相位值φp；

本桥梁工程采用双向四车道高速公路标准，设计时速100km/h，桥面宽25.4m，结构物设计荷载为Ⅰ级，设计安全等级为一级，标准跨径30m单幅桥梁为四片，梁间距2.719m，预制梁高1.5m。本桥梁位于直线段上，左右幅均为1.5%横坡，桥梁桩基由钻孔灌注桩变更为人工挖孔灌注桩，承台基础采用圆孔挖孔灌注，持力层主要是中等风化灰岩。

Step2 群时延相位估计：

φ=[φ(0),φ(1),…,φ(M-1)]，

Step3 相位噪声估计：

(1)根据公式(15)计算不同导频处相位噪声ψp(b)；

Step4 相噪群时延联合频域响应估计：

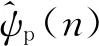
输出参数δ。

3 算法仿真与分析

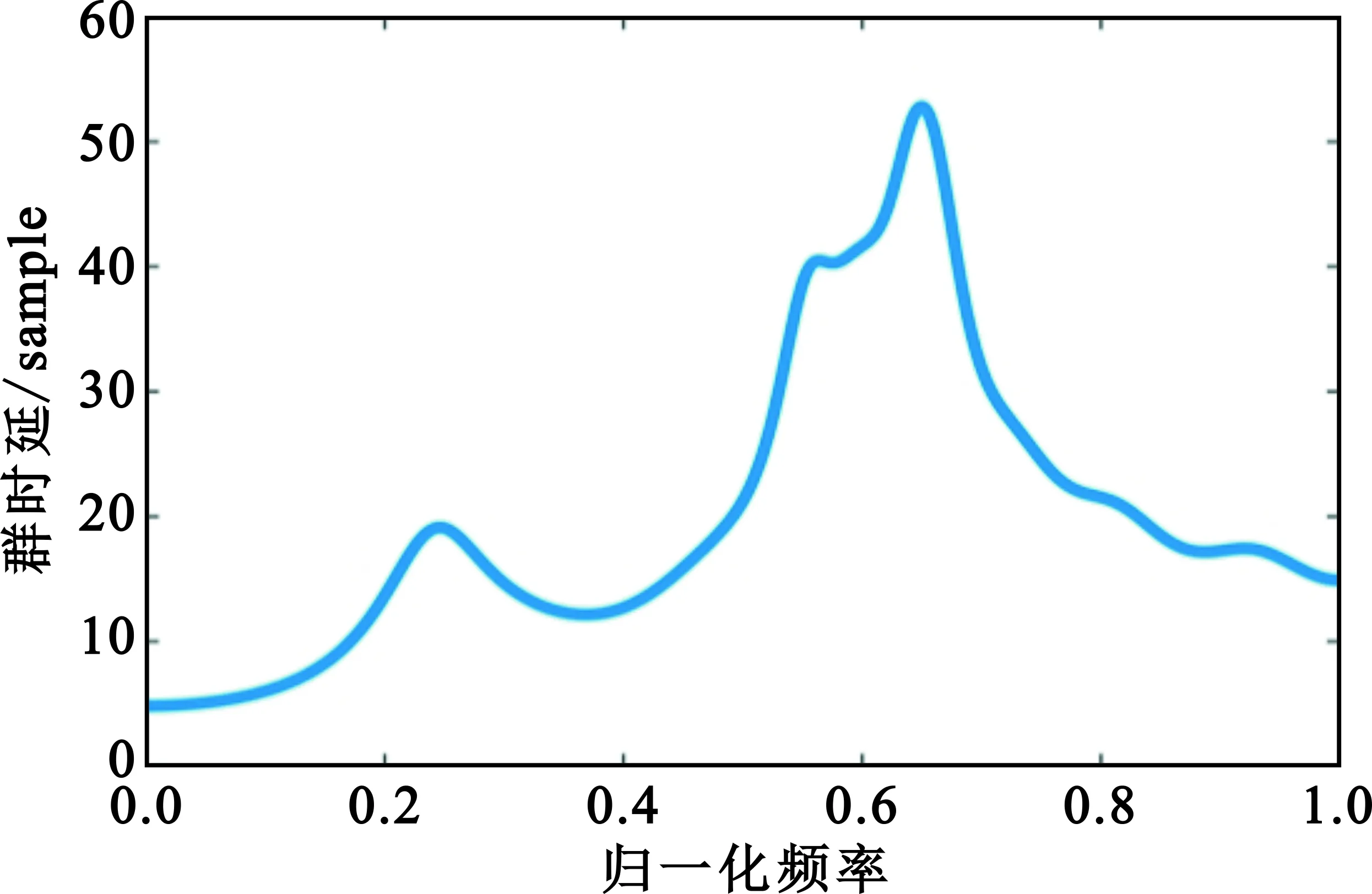
图3 仿真使用的群时延频域响应

其他的仿真参数如表1所示。

表1 仿真参数

图4为本文联合估计算法与其他算法在相位估计均方误差(Mean Square Error,MSE)上的比较结果。其中只估计相位噪声的算法为文献[11]采用的线性内插估计算法，而只估计群时延的算法为文献[8]采用的频域滤波器群时延拟合算法，分离估计相位噪声和群时延的算法首先通过相噪估计算法消除相位噪声，再利用滤波器估计群时延。

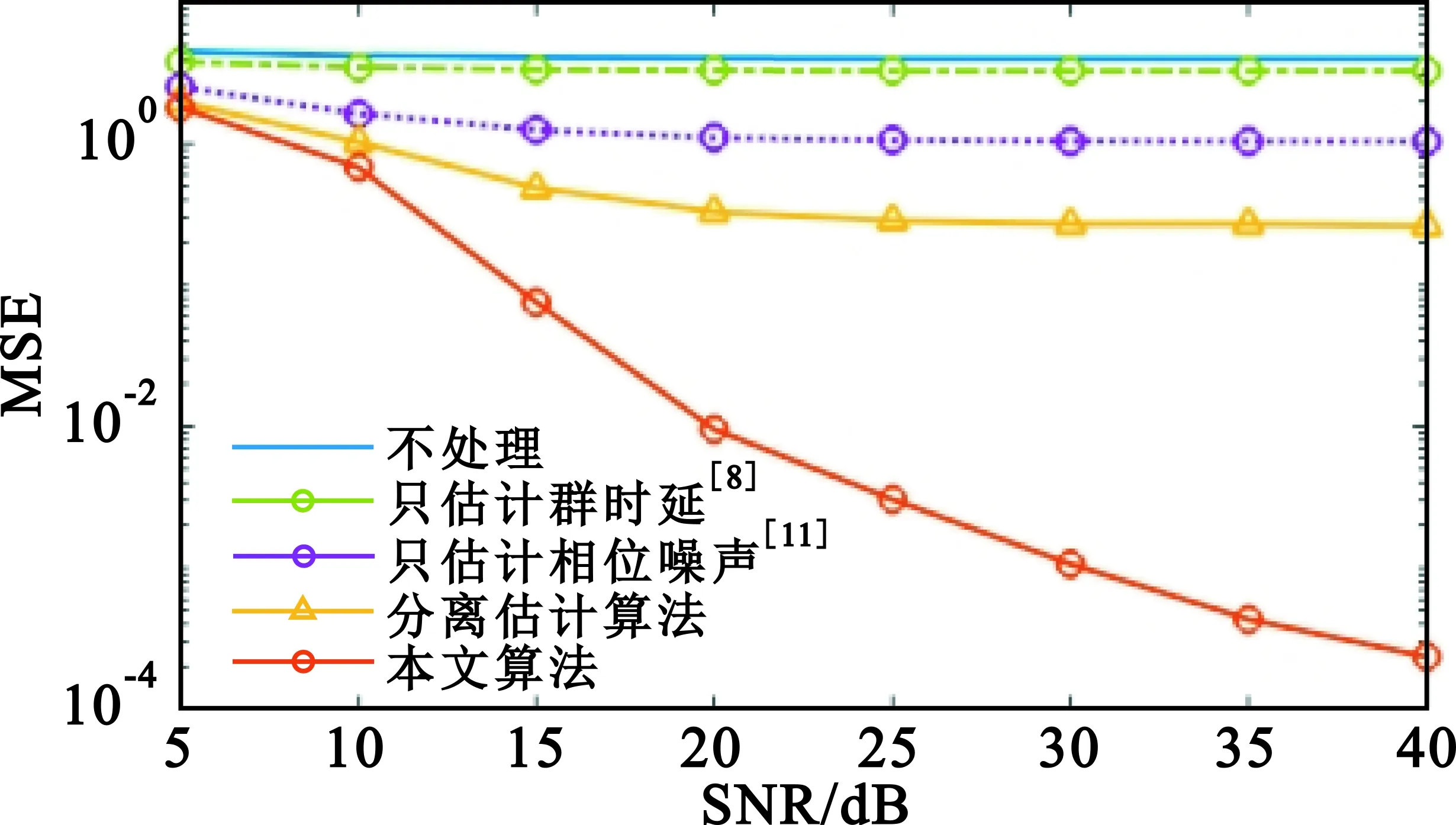
图4 不同算法下相位估计MSE

如图4所示，若不消除系统中的相位噪声和群时延，则相位失真的估计有着严重的误差，提升系统的信噪比(Signal-to-Noise Ratio,SNR)并不能提升相位估计的准确度。仅消除单个因素造成的相位失真，也存在着较大的误差。而对比分离估计相噪群时延的算法，本文算法在抑制相位失真上也有着更好的准确性，在信噪比为15 dB时分离估计算法MSE约为0.5,本文算法MSE约为0.05。其优势随着信噪比的增大逐渐增大，在信噪比为30 dB时本文算法并不会出现其他算法面临的平底效应。同时，本文算法不需要提前测量以获知信号传输过程中的群时延参数，有利于系统的实际应用。

图5所示为不同导频插入密度下，联合估计算法和分离估计算法相位估计MSE的对比结果。

图5 不同导频密度下的相位估计MSE

由图5可见，本文所提算法导频插入密度越高，相噪群时延联合估计算法对于相位失真的估计准确度越高。而分离估计算法随导频插入密度变化较小，几乎重合，这是因为相噪和群时延耦合作用后分离估计的误差较大，提升导频密度也难以提升准确度。本文算法在15 dB信噪比、[L,K]=[32,10]时相较于分离估计算法误差降低了约40%。而随着导频插入密度的增加，联合估计算法的MSE性能优势进一步增大，说明本文算法在低密度导频设置下和高信噪比时，相较于分离估计的算法优势更加明显。

根据第2节的算法步骤可知，本文所提联合估计算法复杂度为O(NaNb+MN)。只估计群时延和只估计相位噪声的算法复杂度分别为O(M+Na)和O(N+Nb)，分离估计算法的复杂度为O(MN+Na+Nb)。对比可知，本文算法以较小的复杂度代价获得了较大的估计性能提升。

4 结束语

本文提出了一种相位噪声群时延联合估计算法，利用非线性群时延的泰勒级数展开模型与相位噪声的连续特性联合估计了相位噪声和群时延导致的相位失真。仿真结果表明，本文算法在不同导频插入间隔下均能够有效估计系统中相位噪声和群时延联合作用带来的相位失真，且明显优于现有分离估计方法。

本文主要考虑了群时延和相噪耦合后造成的公共相位误差估计，而在未来的工作中将进一步考虑相噪和群时延效应带来的载波间干扰估计。