一种面向LTE-V2X的联邦学习信道估计算法 *

景兴红，尹子松，蔡志镕，何世彪，廖 勇

(1.重庆工程学院 电子信息学院，重庆 400056；2.重庆大学 微电子与通信工程学院，重庆 400044)

0 引 言

近年来，随着车联网的快速发展，车载用户对高可靠低时延通信(Ultra-Reliable Low Latency Communication,URLLC)提出了需求。单载波频分多址(Single-Carrier Frequency-Division Multiple Access,SC-FDMA)由于具有峰均功率比较低的优点，已被用作车联网通信协议LTE-V2X的传输方案[1]，而信道估计作为SC-FDMA系统的重要环节，直接决定了通信系统的可靠性。在车联网环境下，车辆处于高速移动状态，导致了严重的多普勒效应，影响信号的正确解调。因此，信道估计在整个通信系统中扮演着关键的角色，为了保障道路交通的安全，需要提高信道估计的准确性。

车联网场景下的无线信道具有快时变的特性[2]，因此可采用基于导频的信道估计方案。传统的信道估计算法包括采用最小二乘(Least Square,LS)或线性最小均方误差(Linear Minimum Mean Square Error,LMMSE)方法估计导频位置的信道状态，再利用线性插值的方法得到数据位置的信道状态，然而这种方法无法追踪高速移动环境下的信道变化。为了跟踪时变的信道，文献[3]引入了增强的均衡方案谱时间平均(Spectral Time Average,STA)，利用来自数据子载波的判决，并同时在时域和频域中进行平均来更新信道估计，提高了车联网下信道的估计性能。文献[4]提出了一种基于长训练导频序列的信道频域响应和构造数据导频(Constructed Data Pilots,CDP)的信道估计方案，该方案利用数据符号构造导频，并利用相邻两个符号内信道间的相关特性，进一步优化信道更新的准确性。文献[5]提出了一种基于迭代检测器和解码器(Iterative Detector and Decoder,IDD)结构的扩展卡尔曼滤波(Extended Kalman Filter,EKF)信道估计方法，利用EKF联合估计信道频率响应和时变时间相关系数，并且采用IDD结构来减少EKF中的估计误差。除了以上的传统方法之外，为了追求更高的估计精度，近年来研究人员开始采用深度学习的方法来估计信道。文献[6]采用全连接网络，利用仿真数据进行离线训练后对时频域选择性衰落信道(双选衰落信道)进行估计。文献[7]将信道响应建模成一个二维图像，采用超分辨率(Super-resolution,SR)算法恢复信道。然后，上述文献中，基于深度学习的方法需要收集大量的信道数据并集中对这些数据进行处理，在传输数据时需要大量的时间和资源，且存在车载用户数据隐私泄漏的问题。

最近，联邦学习已经被提出用以训练模型[8]，相较之前的深度学习网络模型训练方式采用的集中式学习(Centralized Learning)，联邦学习将学习过程分布在多个不同的用户上进行分布式学习(Distributed Learning)。通过这种方式，大量的训练数据无需传输到中心服务器上；另一方面，学习过程中的计算负载从中心服务器转移到每个用户上，极大减少了服务器的负担。

为此，本文提出了一种基于联邦学习的LTE-V2X信道估计方案，主要贡献如下：

(1)采用CNN-LSTM-DNN模型对信道进行估计，该网络首先利用CNN对信道进行特征提取导频处的信道响应，之后采用双向LSTM网络估计出数据处的信道响应，最后使用DNN对信道响应进行降维。

(2)提出一套基于联邦学习的信道估计框架。训练信道估计网络时，需要计算大量参数，利用联邦学习能够将计算负载转移到多个车载用户上，车载用户无需上传大量的信道数据至基站，有效节省资源的同时还保护了数据隐私。相较传统的信道估计算法，本文所提方法的归一化均方误差(Normalized Mean Square Error,NMSE)和误码率(Bit Error Rate,BER)均有较大提升。

1 系统模型

1.1 SC-FDMA系统收发机信号处理

SC-FDMA系统的基带传输模型如图1所示。在发射端，用户数据经过了离散傅里叶变换(Discrete Fourier Transform,DFT)预编码、子载波映射、快速傅里叶逆变换 (Invert Fast Fourier Transform,IFFT)、添加循环前缀(Cyclic Prefix,CP)，与此同时，由ZC(Zadoff-Chu)序列产生的导频经过载波映射、IFFT、添加CP并与用户数据一同发射至空间。接收端的处理过程与发射端相反。由于信号受到信道衰落与噪声的影响，需要对信道进行估计并在快速傅里叶变换(Fast Fourier Transformation,FFT)之后采用频域均衡补偿信道造成的影响，进而完成信号的检测。

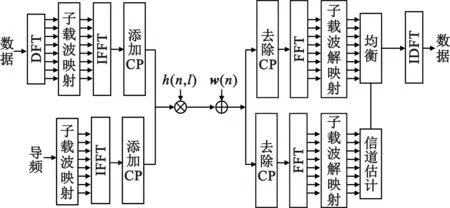
图1 SC-FDMA基带等效传输模型

1.2 SC-FDMA系统传输模型

对于SC-FDMA传输模型，假设系统的子载波数量为N，对于第i个SC-FDMA频域符号Xi∈CN，Xi=[Xi(0),Xi(1),…,Xi(N-1)]T，Xi(n)表示第n个子载波的频域符号。Xi经过IFFT变换之后调制为时域符号xi∈CN：

xi=FHXi。

(1)

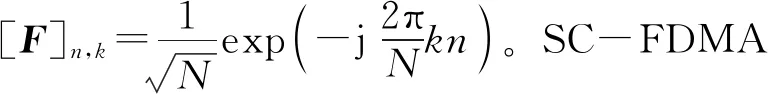
yi=Gixi+wi。

(2)

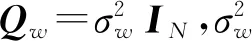
(3)

式中：hk,l表示第l个抽头的第k个采样点信道冲激响应。时域接收符号yi经过FFT可以得到频域的接收符号Yi∈CN×1：

Y=Fy=FGFHX+Fw=HX+W。

(4)

式中：Hi∈CN×N表示第i个SC-FDMA符号的信道频域响应矩阵，并且有

H=FGFH。

(5)

在一个SC-FDM符号持续时间内，每个抽头的系数变化缓慢，该抽头系数不变[9]，此时的G为托普利兹矩阵，故H为对角矩阵[9]：

(6)

根据式(6)，式(4)可以改写为

Y=SH+W。

(7)

式中：S为对角矩阵，其对角线上的元素为X；H为矩阵H对角线上的元素。传统的信道估计方法有LS、LMMSE估计算法。LS算法估计如下：

(8)

(9)

式中：D=Rhh(Rhh+(SSH)-1σ2I)-1，Rhh为信道自相关矩阵，文献[10]给出了详细的计算过程。

2 联邦学习信道估计

2.1 信道估计网络模型训练框架

基于联邦学习的信道估计网络训练过程与传统的集中式训练不同的是，联邦学习不需要将训练数据上传至基站，基站也不需要花费大量的计算资源在更新网络的参数上。采用联邦学习训练信道估计网络的过程如图2所示。

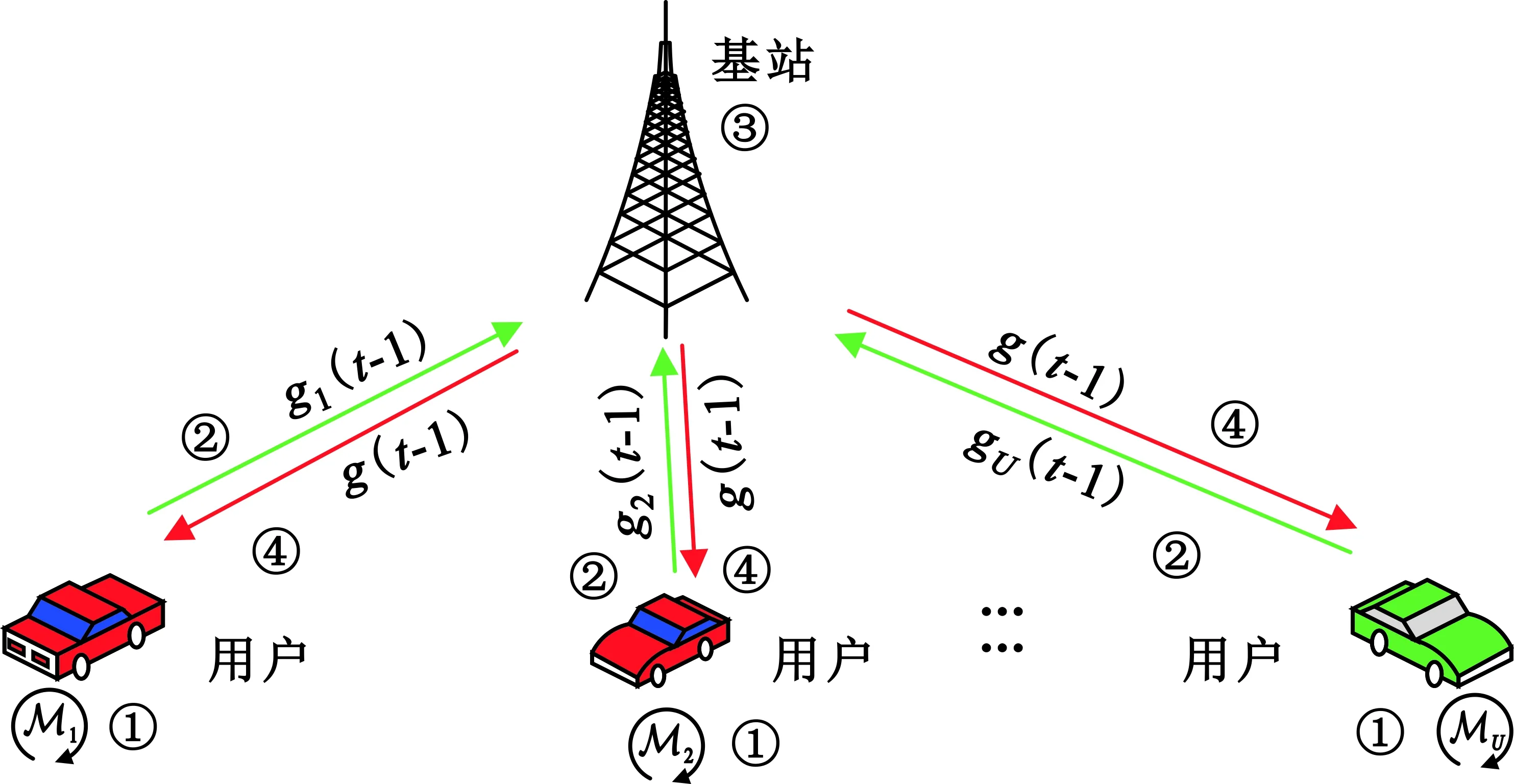
图2 基于联邦学习的信道估计网络训练框架

Step2 参数上传。U个用户上传计算的参数{g1,g2,…,gU}至基站。

Step3 参数聚合。 基站计算U个参数的平均值g。

Step4 参数反馈。基站将更新的参数g广播到U个用户中，每个用户基于参数g更新网络的参数。

在Step 1中，每个用户计算网络的参数，网络模型采用CNN-LSTM-DNN，其原理和细节详见2.2节。

2.2 CNN-LSTM-DNN网络模型

CNN-LSTM-DNN信道估计网络结构主要分为离线训练、在线估计两个部分，如图3所示。

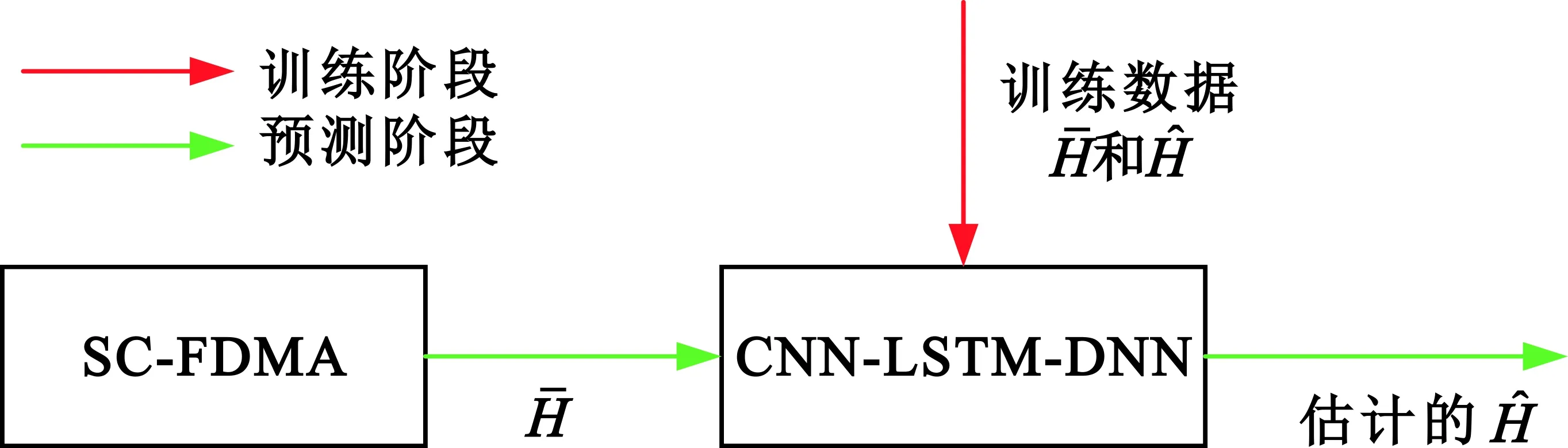
图3 CNN-LSTM-DNN信道估计网络结构

本文所使用的信道估计网络主要分为两个步骤。首先，需要对CNN-LSTM-DNN进行训练，其目的是调整CNN-LSTM-DNN中的参数。需要做的就是收集足够多的信道数据样本，然后使用这些信道数据样本对CNN-LSTM-DNN算法进行训练，通过训练迭代求解该算法最小均方误差下的最优参数，即使其学习到信道的变化特征。对于估计阶段，此时CNN-LSTM-DNN算法中的参数已经训练完成，因此直接将训练好的CNN-LSTM-DNN用于跟踪信道的变化，完成在线信道估计。因此，此时CNN-LSTM-DNN的输入为SC-FDMA无线通信系统中每帧的信道矩阵。CNN-LSTM-DNN主要由CNN、双向LSTM(Bidirectional LSTM,BiLSTM)和DNN组成，其结构图如图4所示。

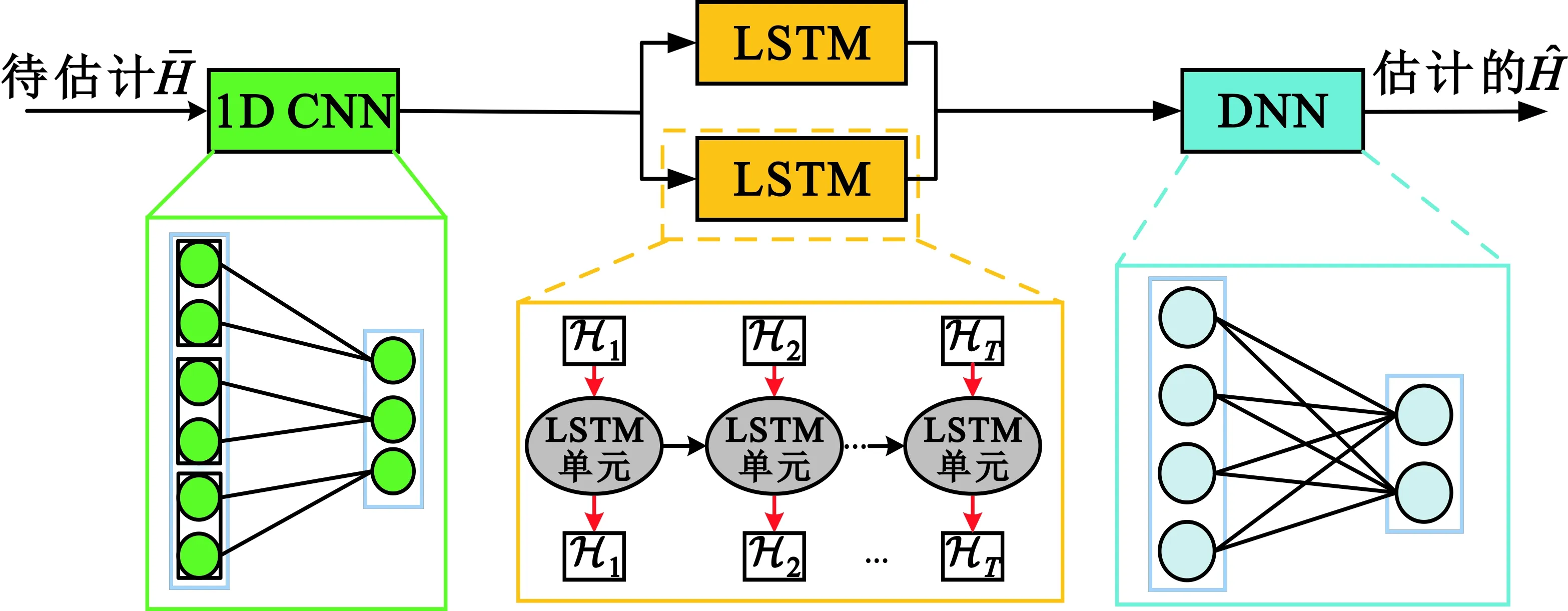
图4 CNN-LSTM-DNN结构

待估计的信道数据通过CNN-LSTM-DNN得到估计的信道数据。下面将详细介绍CNN-LSTM-DNN中的输入数据预处理、CNN特征提取、时域信道估计和数据降维。

2.2.1 输入数据预处理

信道估计的目的就是在接收端估计出信道频域响应矩阵H，而对于基于导频辅助的信道估计方法，其目的是通过导频符号处的信道响应估计出数据符号处的信道响应。对于CNN-LSTM-DNN信道估计算法，其输入为一个子帧大小的信道频域响应矩阵，该矩阵中导频符号位置处的信道响应通过LS方法初始化，而数据符号位置处的信道响应数值被设为0，其输入数据表现形式为

(10)

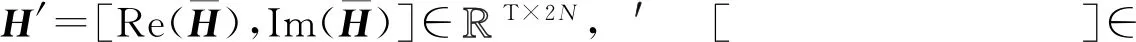
2.2.2 CNN特征提取

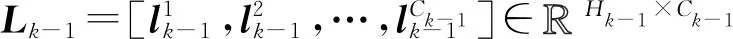
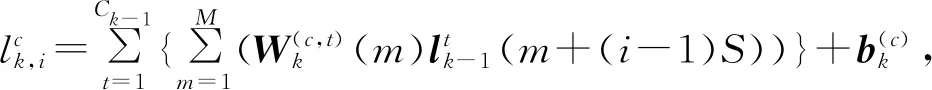
(11)

式中：Wk∈RCk-1×Ck×M和bk∈RCk分别表示第k层的权重张量和偏置矢量，S为卷积滤波器在输入数据上滑动的步长，M表示卷积滤波器的宽度，Ck表示第k层卷积神经网络输出的通道数。因此可以得到第k层一维CNN上第c个通道上的输出矢量为

(12)

故第k层的输出数据为

(13)

同样地，为了使得数据进行非线性变换，每层一维CNN网络后面需接激活函数，因此一维CNN每层的变换公式可以简写为

Lk=f(Wk*Lk-1+bk)。

(14)

对于基于一维CNN的频域特征提取，使用的卷积核宽度M=9，步长S=1，一维CNN的输入和输出通道数为T，于是第t个SC-FDMA符号上第n个子载波上的特征为

(15)

对于每个SC-FDM符号提取特征后的输出可以表示为

(16)

式中：t对应1D CNN中输出的第t个通道数。

2.2.3 LSTM时域状态估计

对于单个LSTM单元，其数学变换式为

it=σ(Uixt+Wilt-1+bi)，

(17)

ft=σ(Ufxt+Wflt-1+bf)，

(18)

ct=ft⊙ct-1+it⊙σ(Ucxt+Wclt-1+bc)，

(19)

ot=σ(Uoxt+Wolt-1+bo)，

(20)

lt=ot⊙tanh(ct)。

(21)

式中：it、ft、ot和ct分别为LSTM网络t时间步的输入门、遗忘门、输出门和记忆单元，lt为t时刻的输出矢量，也为流向下一个时刻的隐藏层矢量，Ui、Wi、Uf、Wf、Uc、Wc、Uo、Wo为LSTM网络的权重矩阵，bi、bf、bc、bo为LSTM网络的偏置;⊙表示元素乘法，σ为sigmoid函数。每个时间步LSTM网络的输出变换式可以简化为

lt=LSTM(lt-1,xt,Θ)。

(22)

式中：LSTM(·)为公式(17)～(21)的组合，Θ表示LSTM网络中的所有参数。故BiLSTM网络t时刻的两个LSTM的输出分别为

(23)

(24)

式中：ΘFW和ΘBW分别为前向LSTM和后向LSTM网络中的所有参数，两个LSTM网络中只有权重没有偏置。于是BiLSTM网络t时刻的输出为

h‴t=[hFW,t;hBW,t]∈R4N×1。

(25)

2.2.4 DNN降维

采用DNN进行降维有两个好处：第一，DNN降维后的输出为输入的加权组合，能够完美地利用输入的所有信息，不会因维度变化而造成信息的丢失；第二，DNN网络能够从前后项估计的数据中选择出最优的数据作为输出，提高最终估计的准确度。于是第t个SC-FDMA符号最终信道估计的结果为

(26)

最后，将最终估计结果的实部和虚部分离出来作为估计的实部和虚部，然后整合成复数的形式得到最终的估计结果。

2.3 模型训练

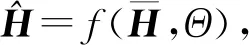
(27)

(28)

常用梯度下降法[11]更新式(28)的参数：

Θt=Θt-1-αΘL(Θt-1)。

(29)

Θt=Θt-1-αt-1ΘLDt(Θt-1)，

(30)

(31)

(32)

(33)

最后将g(t-1)反馈到每个用户，并进行参数更新：

Θt=Θt-1-αt-1ΘLDt(Θt-1)。

(34)

2.4 信道估计

完成网络模型的训练之后，即可估计信道，估计过程如图5所示。

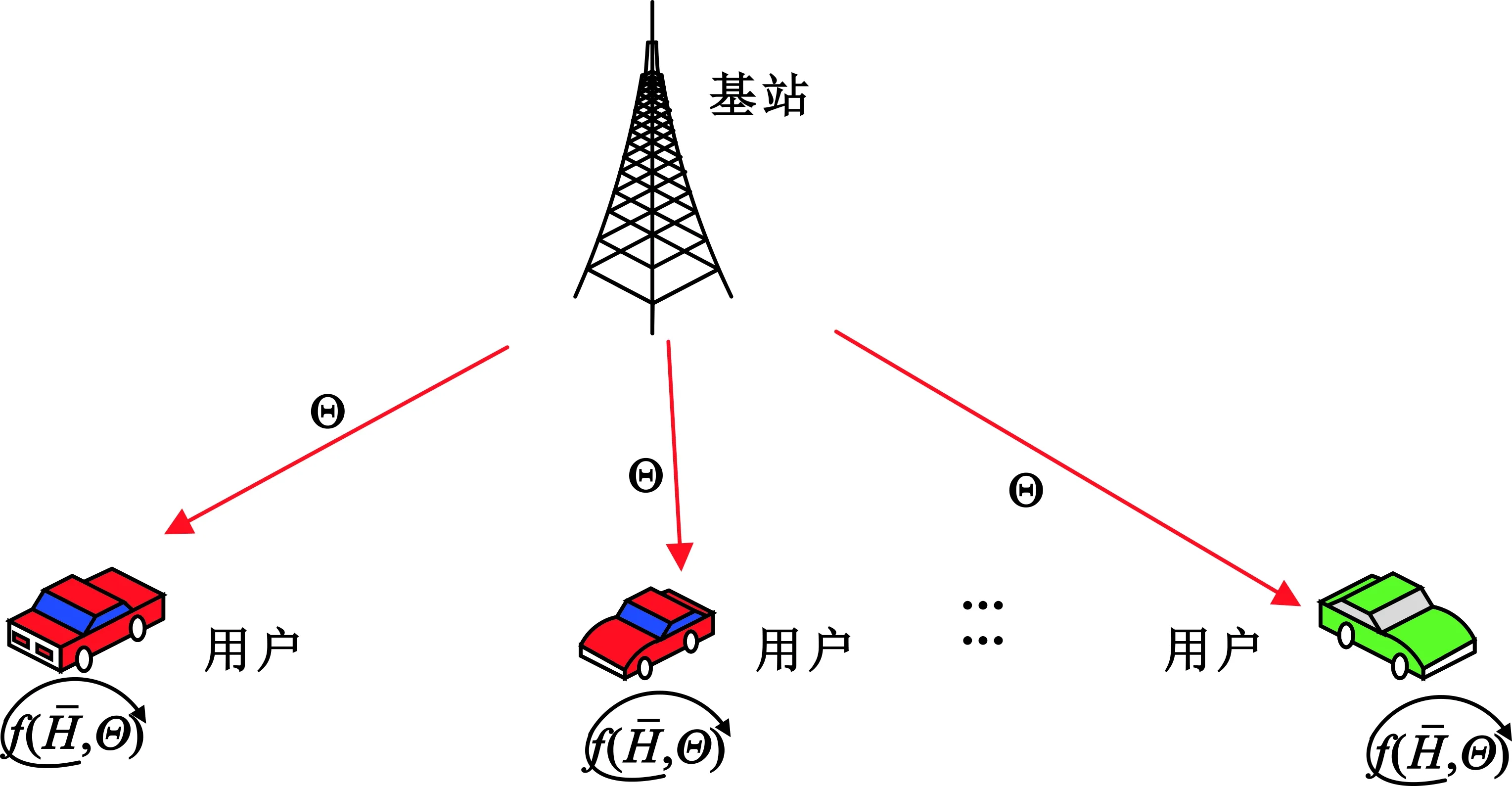
图5 信道估计示意图

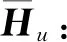
(35)

(36)

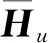
(37)

至此，我们完成了完整的面向车联网场景的基于联邦学习的信道估计设计与推导。

3 仿真与复杂度分析

3.1 仿真分析

本节对所提方法进行仿真分析，对于LTE-V2X物理层的帧结构、导频结构等参数按照3GPP协议设定，具体的仿真参数如表1所示。

表1 仿真参数

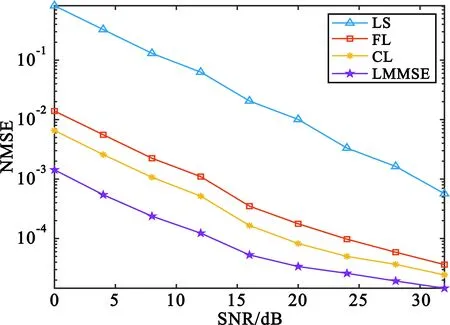
仿真算法除了本文所提的基于联邦学习的算法(FL-based)之外，还包括了集中式训练(CL-based)算法、LS信道估计算法、LMMSE信道估计算法。指标包括归一化均方误差和误码率。图6对比了LS算法、LMMSE算法、集中式训练的算法以及联邦学习算法在车辆运行速度为30 km/h时的NMSE性能以及BER性能。从图中可以看出，四种算法的NMSE皆随着信噪比(Signal-to-Noise Ratio,SNR)的提升而减小,由于充分利用了信道的统计信息以及噪声的信息，且终端在低速运动时数据处的信道响应变化不大，所以LMMSE算法的性能最好。而基于分布式训练的联邦学习算法与集中式训练的算法较为接近，两者的性能均大幅度领先LS算法，略低于LMMSE算法。LMMSE算法BER性能最优异，较LS有5 dB左右的增益；联邦学习算法和集中式学习算法的性能在LMMSE和LS中间。进一步对比两者可以看出，基于联邦学习算法的BER性能仅仅落后集中式学习算法1 dB左右，较LS相比都有3 dB以上的增益。

(a)NMSE vs. SNR

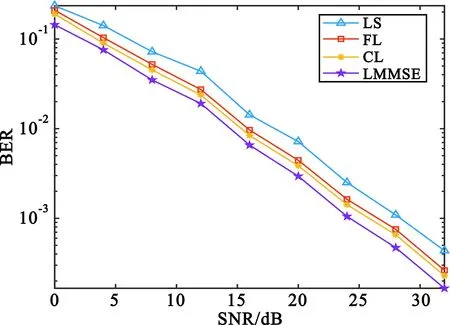
(b)BER vs. SNR图6 车辆运行速度为30 km/h时四种算法的NMSE和BER性能

图7对比了四种算法在车辆运行速度为150 km/h时的NMSE性能以及BER性能。此时，由于终端运行速度快，所以LS算法以及LMMSE算法的NMSE性能在SNR为15 dB以后无法再取得进一步的提升，而LMMSE算法在低SNR的情况下较联邦学习算法以及集中式学习算法有微弱的优势，这是由于低SNR环境下，噪声的影响较大，此时导频位置处的估计精度占主要因素，一旦SNR提高，传统算法无法有效追踪变化的信道，而采用深度学习的方式能够克服这一点。从图7可以看出，随着SNR的提高，联邦学习算法和集中式学习算法均能继续提高估计的精度。在信噪比大于8 dB时，联邦学习算法的NMSE性能超过了LMMSE算法，并且紧随着集中式学习的算法，仅有2～3 dB的落后。观察四种算法的BER性能，仍可以得到类似的结论，即采用深度学习的方式估计信道较传统的方式有大幅度的提升，其中联邦学习算法的性能紧随集中式学习算法，两者仅有1 dB左右的差距。

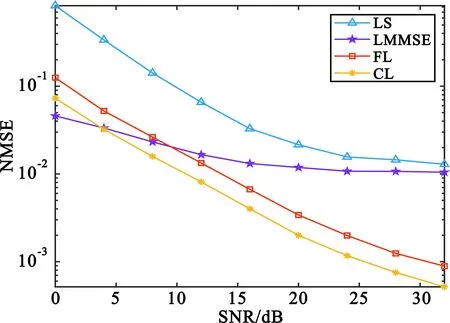
(a)NMSE vs. SNR

3.2 复杂度分析

LMMSE和LS两种传统算法和所提算法的计复杂度的对比如表2所示。

表2 时间复杂度分析

从表2中的结果可以看出，所提算法时间复杂度低于传统的LMMSE算法，高于LS算法。所提算法仅仅是一些矩阵的乘法和加法运算，因此其复杂度低于传统的LMMSE算法;并且，神经网络可以并行运行，因此可以减少算法计算时间。对于在线估计阶段，此时直接将训练好的网络用于信道估计，因此复杂度较低。对于信道条件的改变，可以依靠先前训练过的网络，并根据现有的数据对网络中的模型进行微调，从而大大降低了训练的复杂度。总的来说，所提算法的复杂度在可接受的范围内。

4 结 论

本文从车联网LTE-V2X通信的可靠性出发，设计了一种面向SC-FDMA系统的基于联邦学习的信道估计算法。针对传统信道估计难以追踪高速移动场景下的无线信道的问题，提出了CNN-LSTM-DNN网络有效估计快时变的信道，并采用分布式的学习方式，一方面减轻了道旁基站的负担，另一方面能够保护车载用户的隐私数据，弥补了集中式训练需要传送大量数据且容易暴露用户隐私的缺点。仿真结果表明，本文所提网络与集中式学习的方法相比仅损失了微弱的性能，与传统方法相比有较大的性能提升。