电子测量技术课程中误差分析理论的教学思考

何宁业，宁仁霞，孙剑

（黄山学院信息工程学院，安徽黄山，245041）

0 引言

电子测量技术是电子信息类、测控类本科专业必修课程。我校电子信息工程专业设置的该课程由理论和实验课组成，涵盖的理论内容包括电压测量、时频测量、阻抗测量等方面知识，实验课涉及多种常见仪器仪表的操作使用方法。课程内容很广泛，但因受教学课时限制，传统的电子测量技术理论课程内容中大篇幅是讲授各种仪器及测量技术的原理，没有过多的重视误差理论。殊不知没有合理的误差分析，有再好的测量技术也是枉然。

由于该课程中不可避免地会讲述各种仪器的原理，并涉及到信号与系统、模电等先修课程的基础知识点，甚至有不少复杂原理图和公式，容易导致部分学生打消学习积极性。本文以误差分析的教学内容为例，对该课程的教学改革做分析说明。

1 误差分析理论

1.1 误差的概念

首先带学生回顾测量的概念，再由此引入误差。测量是为了确定被测对象的量值而进行的实验过程。在此过程中，该量本身所具有的真实大小为真值，实际测得的为测量值，两者差值就是所谓的测量误差，如式（1）所示。

需要注意的是，此处的真值，是指与给定的特定量的定义一致的值。它是一个理想的概念。但真值虽客观存在，却难以获得。正因为其难以获得，实际应用中是用所谓的“参考量值”来替代，即：

教学中可借用具体案例来说明以下三种确定参考量值的方法：

①“参考量值”可由理论（或定义）给出；

② 用“约定真值”代替“真值”；

③ 用“不确定度”评定测量结果。

1.2 误差的表示

常见的用来表示测量误差两种方法分别是绝对误差和相对误差。传统课堂教学中重点是放在给学生讲授两种误差的定义和表达式。

绝对误差即被测量的测量值与真值之差，如式（3）所示，x表示测量值，A为真值。

相对误差则有多种表示形式，其中最常用的为测量值相对误差（示值相对误差）xγ，是指用绝对误差Δx与仪器测得指示值之比来表示（百分数），记为式（4）

另外，需特别提醒学生注意满度相对误差γm的概念。它多用于电工仪表的等级划分，具体表达式如式（5），其中xm为仪表量程最大值，S为仪表等级，一般分为7个等级。

1.3 误差的分类

按照误差的性质可将误差分为系统误差、随机误差和粗大误差。

随机误差，顾名思义就是误差按照不可预定方式变化，在等精度测量条件下，误差的绝对值和符号都是不定值。但是我们可以采用概率论与数理统计课程中统计学思想来分析此类误差，研究其期望和方差，利用正态分布的方法来观测此类误差。

系统误差是由固定不变或按确定规律变化的因素所造成，按照规律特征不同，可将系统误差分为恒定系统误差和变值系统误差。讲授这部分内容时可借助提问的方式，引导学生自行学习，边学边思考两类不同系统误差判定和处理方法有何不同，并结合书上实例理解各种方法具体如何实施操作。

粗大误差在一定条件下，测量值显著偏离其实际值所对应的误差。主要表现为读数错误、测量方法错误、仪器有缺陷、电磁干扰及电压跳动等。粗大误差无规律可循，故必须当作坏值予以剔除。剔除是要有一定依据的。在不明原因的情况下，首先要判断可疑数据是否是粗大误差。剔除方法的基本思想是给定一个置信概率，确定相应的置信区间，凡超出置信区间的误差就认为是粗大误差。

2 误差分析的教学思考

2.1 掌握误差的表示

相比以上灌输式教学方法，更重要地是让学生理解绝对误差和相对误差这两种表示方法的区别，以及在不同场景下如何选用合适的误差表示方法。积极引导学生思考为什么有了绝对误差这种表示方法还要用相对误差？具体可借助两只电压表测量精度比较的例题来讲解说明，明确绝对误差主要用于表明测得值偏离实际值的程度，而相对误差则用于表示测量的准确程度，典型应用如电工仪表用满度相对误差来描述仪表精度。在电子测量技术课堂教学中积极鼓励学生发现问题，思考并解决问题。

2.2 理解误差的来源

常见的误差来源有以下五种类型：仪器误差、方法误差、理论误差、影响误差、人身误差。在课堂理论教学中有必要向学生强调找到误差产生的原因是为了更好地从源头上解决误差处理问题，提醒学生在进行电子测量方案设计时，就应该全面考虑可能引起较大误差的因素，从而优化设计或实验方案。

2.3 明确误差的关系

从定量分析角度而言，按照误差的定义式将三种误差之间满足的关系用下式（6）描述。即误差由系统误差ε、随机误差δ求和得到，其中粗大误差不出纰漏的正常情况下不应存在。

从定性的角度，系统误差ε小对应就是测量的正确度较高，随机误差δ小则对应测量的精密度小，若两者误差都很小，则称之为精确度很高，可用如下打靶射击示意图直观描述以上三种情形，图中A为真值。利用图示法更加直观有效，有助于进一步加深学生对系统误差和随机误差这类抽象概念的理解，做到心中有数。

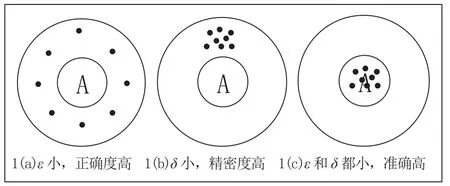
图1 打靶射击示意图

2.4 承认误差存在的客观性

误差只能尽可能减小，很难做到绝对消除。从误差的类型上来看，粗大误差一般都是人为操作不当或者设计方案出现重大纰漏导致的，一般可以通过周密考虑尽量避免。但是系统误差和随机误差却不尽然，特别是随机误差，单从它的名称中就可以了解到此类误差的随机无规律性。因此，对于一个严谨的电子测量方案设计者而言，方案设计时应该是尽可能避免粗大误差，同时减小系统和随机误差。

3 结语

本文从电子测量技术课程的特点和教学现状出发，以误差分析理论的相关内容为例，讲解如何引导学生积极思考，理解误差概念，掌握误差理论，学会分析误差的来源和规律，识别误差的性质，在一定测量条件下，尽力设法减少误差，保证测量误差在容许的范围内。