基于正交实验法的Web测试用例设计
刘志成
(公安部第三研究所,上海,201204)
0 引言
日常的Web测试工作中,首先需要做测试用例设计,如果输出的用例,需要验证的组合太多,甚至是海量组合时,就需要投入较大的人力成本,来一一验证,必然是事倍功半的。因此如果运用正交实验法,科学有效的选择一部分有代表性的组合进行测试验证,就可以达到事半功倍的效果,提高工作效率,降低成本投入。
1 正交实验法应用
1.1 正交实验法介绍
正交实验法是研究多因素多水平的一种设计方案,主要是根据Galois的理论,从所有可能的实验中筛选出具有代表性的部分组合,来完成实验。简而言之,就是应用正交表,挑选部分具有有代表性的组合进行实验,并对其结果进行分析,从而找出最优的组合。它可以在毫无规律的情况下,通过数据均匀分布的特性,完成日常测试工作中的用例设计,可以非常直观地减少测试用例,降低测试人力成本。
日常工作中,具体应用正交实验法的时候,其实就是使用正交表来设计具体的组合,并实施实验和数据分析[1]。正交表具有下两个特性:任两列中,同一横行所组成的数字对出现的次数相等[2];任一列中,不同数字出现的次数相等。
常见的正交表有L4(23),L9(34),L8(27),具体如下:
1.2 确定因子和水平
针对具体项目中的测试需要,采用方差或极差的分析方法,来对相关的测试对象进行分析,找出对测试目标影响最大的因素和水平组合[3]。
正交表其实是通过概率学和组合数学共同计算得出一种表格,一般用Ln(mk)表示,L代表是正交表,n代表正交表的行数,k代表因子个数,m表示每个因子的水平数。
在针对某项具体的实验时,可以把影响实验结果的项称为因素,简称因子。因子其实就是实验过程中的一个变量,实验结果就是这个变量所属函数运行后的结果。在实验整个过程中,每个因子都可能处于不同的状态或取不同的值,把因子所处的状态或取值,称为因子的水平,简称水平[4]。
日常工作中,负责某个业务的测试工作时,首先需要设计测试用例,就需要先确定因子数和水平数,因子之间需要分析关系后才能确定,水平则需要应用等价类分析法来确定。
例如,Web系统中常见的数据多条件查询功能,现针对该功能进行测试用例设计,功能描述如下:
数据查询功能,支持”创建时间”,”创建者”,”类型”,”内容”等条件类型,且多条件之间互为”且1”的关系。
分析:很明显是4个因子,即”创建时间”,”创建者”,”类型”,”内容”;确定水平需要运用等价类分析法,分析后可确定水平数是3,即1-已存在,2-不存在,3-空。
结果:可以认为被测功能的4种类型都对应有3种输入取值,分别是:系统中已存在的值,系统中不存在的值和空值。
1.3 正交表选取
参考2.2小节,被测功能一共有4个因子,每个因子的水平数都为3。选取正交表时要考虑因素(变量)的个数,考虑因素水平的个数,考虑正交表的行数,取行数最少的一个,因此经过分析,可以选定正交表L9(34),详见表4。
1.4 生成测试用例
针对被测功能,采用正交表L9(34)设计测试用例,现在只需要将2.2章节中确定的因子和水平,套用进表1中,完成替换即可,结果见表5。

表1 L4(23)正交表
得到的表2,对应的每一行就可以当做测试用例,但需要补充完善下,因为表1中存在缺陷,就是缺少全为2和全为3的场景,接下来补充进表2中,完成最终用例,详见表6。

表2 L9(34)正交表
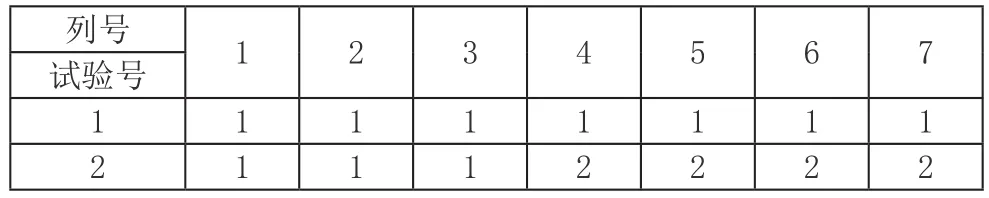
表3 L8(27)正交表

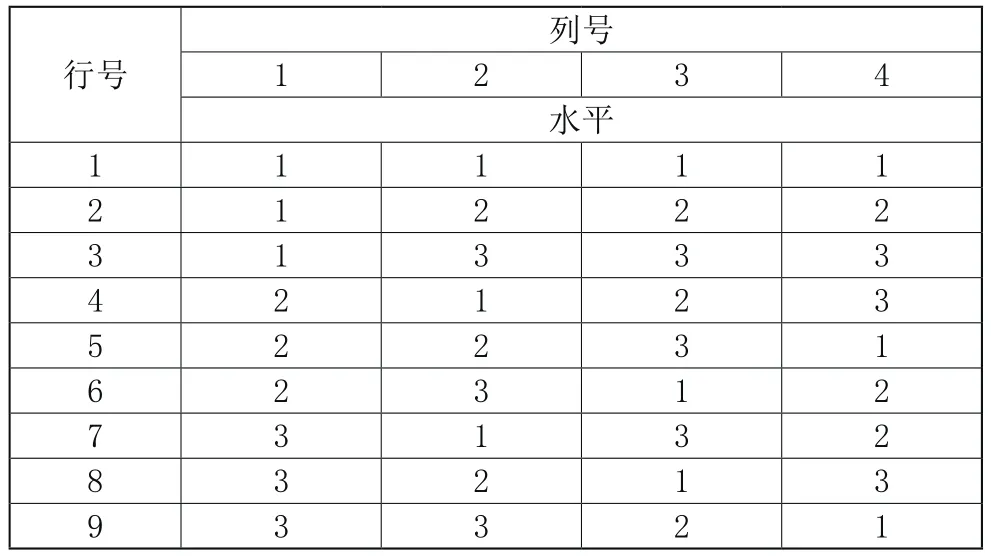
表4 正交表L9(34)

表5 结果
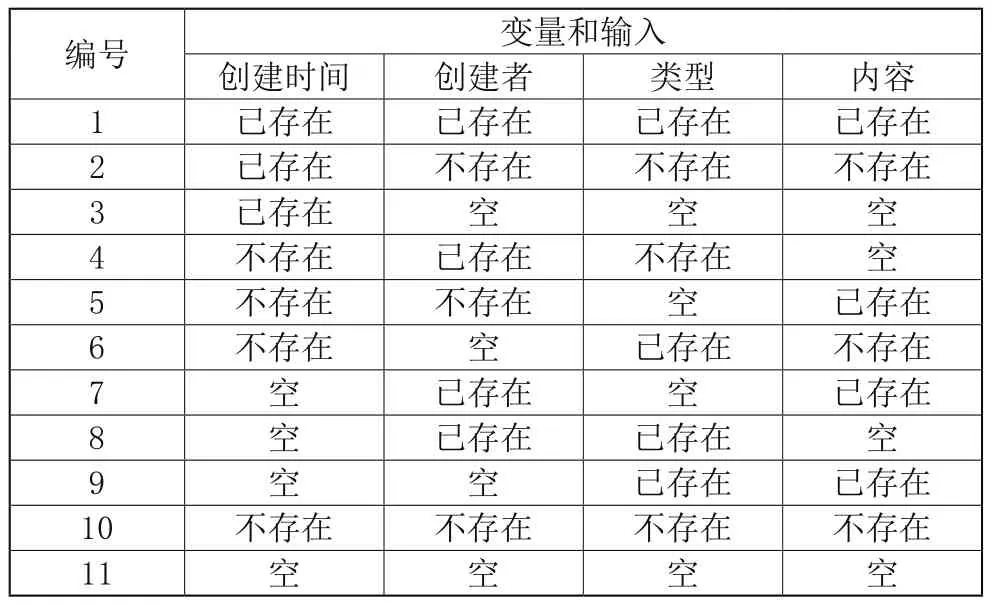
表6 结果
2 结束语
本文的核心其实就是正交表,即一个具有普遍共性的表格,适用于各个领域,可以规划多个因素和水平进行实验,以找出最优水平组合的正交组合设计、正交设计和正交旋转设计等。正交表本质上是选择了所有实验组合中的具有科学代表性的那一部分。因此,在测试设计用例阶段,应用正交表,就可以在过滤掉大部分非代表性的用例的情况下,来相对快速地完成测试工作,从而大大节省工作量,降低人力成本。当前,大数据相关的Web系统在各个领域的中,都承担着至关重要的作用,作为此类系统的心腹之地,把数据查询功能做好,就显着尤为重要,而正交实验法的使用,正是针对此类功能进行测试的一种有效手段。依据正交实验灵活、科学、有效的特点,测试工程师能在条件不好或者看似不可能完成的情况下对大数据Web系统进行充分且高效的测试。
当然,正交实验法也不可能是完美的,在测试工作中,工程师应该根据被测系统的实际业务情况,正确运用该方法并结合其他测试方法,共同完成测试设计,对被测系统完成更全面的测试。

