一种基于FCM算法的电力企业人才甄选策略
吕金历,孔宁,白望望,冯智慧
(1.国网甘肃省电力公司经济技术研究院,甘肃兰州730050;2.兰州理工大学电气工程与信息工程学院,甘肃兰州730050)
随着特高压电网与智能电网建设的快速推进,电力企业面临着专业领域内高素质复合人才的紧缺。人才的紧缺已经为企业人才管理敲响了警钟,使其必须认真分析并应用更加科学的方法来优化人才配置[1]。然而,要优化人才配置,首要任务是要对人才进行有效甄选。
通常,企业对人才综合能力评价是借助传统的人才资源理论,从经验、绩效等方面对人才进行人为的评价[2],存在着一定的主观性和片面性。而人才综合能力评价应具有全面性、灵活性、客观性以及可靠性等特点。为适应现代人才的评价、甄选,K-means聚类算法、神经网络算法、层次分析法等机器学习算法被广泛应用。针对传统人才甄选方式的不足,文献[3]将 K-means聚类引入技术创新人才挖掘,可较好地对高维数据进行分析,减少人为主观性影响。文献[4]提出一种基于密度方法选择初始中心的K-means改进聚类算法,克服传统K-means算法选点随机性对结果的影响。文献[5,6]针对人才综合能力评价问题,提出基于层次分析法的人才综合评价方法,为评价指标提供可实施的量化方法,使得人才评价过程客观化、公开化、透明化。文献[7]在考虑人才考评工作复杂性、人类思维模糊性和指标属性模糊性后,提出基于模糊层次分析法的专业技术人才评价方法。文献[8]针对人才甄选的客观性、灵活性等特点,提出基于模糊神经网络的人才甄选系统,从而提高甄选结果的有效性。文献[9]针对人才评测甄选中的决策问题,建立基于多层次灰色决策的评测甄选模型,将定性分析和定量分析相结合,提高了测评结果的直观性、科学性和客观性。
针对目前人才聚类过程中无法灵活、高效处理非线性高维数据的问题,本文研究一种基于FCM算法的人才甄选方法。该方法是一种基于目标函数的聚类算法,在客观、有效的数据支撑下,可较好处理高维非线性数据。同时,FCM算法将模糊理论引入传统聚类方法,使人才甄选结果在保持全面性和客观性的基础上,又具有一定灵活性。
1 人才综合能力评价指标及数据处理
1.1 评价指标体系建立
FCM算法的运行需要可靠的数据支撑,构建一个客观、完善的评价指标体系,有助于提高实验样本数据的有效性,从而提高人才甄选结果可靠性。现构建人才综合能力评价指标体系[10,11],如图1所示。
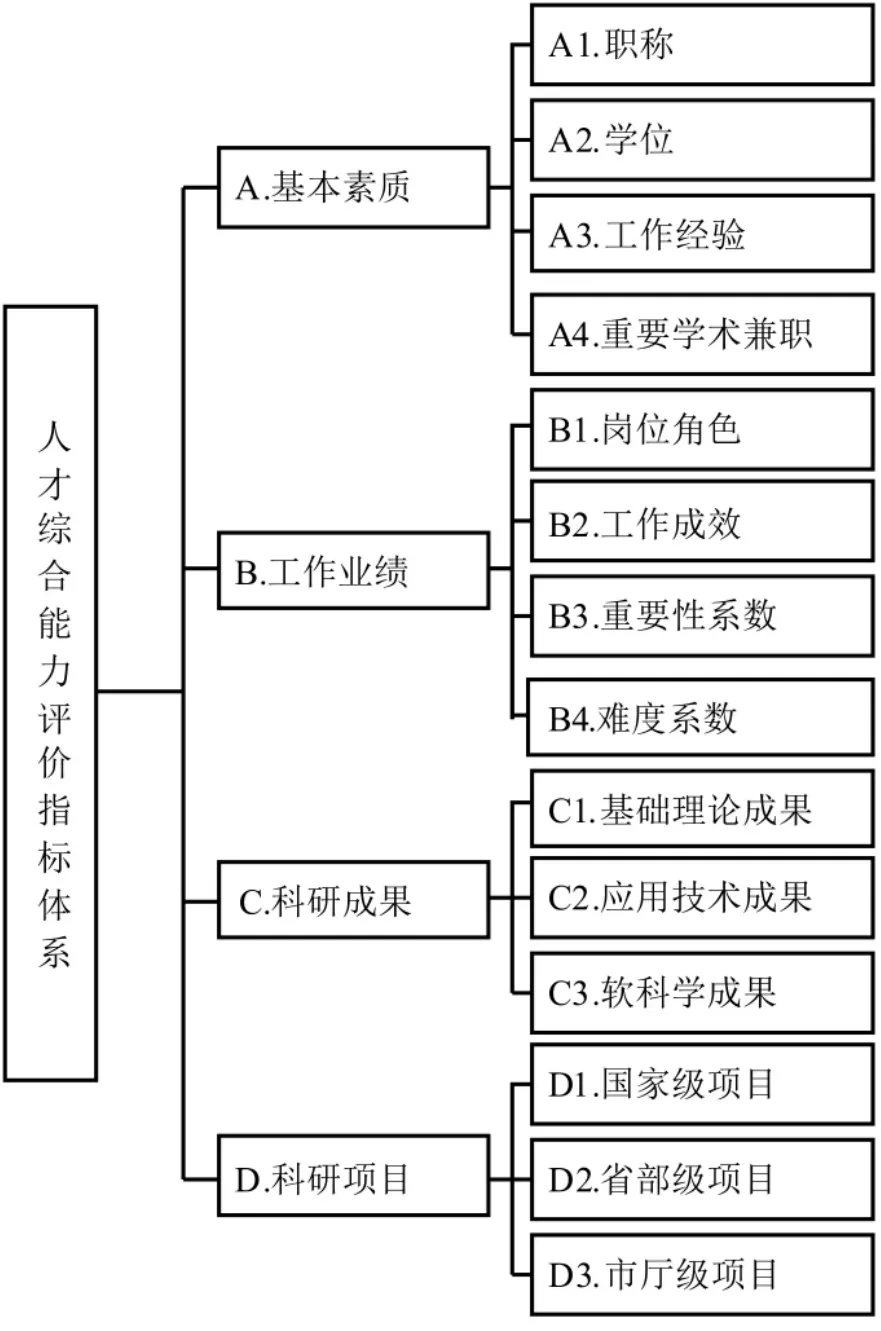
图1 人才综合能力评价指标体系
为对人才综合能力有一个可靠、全面的评估,确保甄选结果的公正性和权威性,发挥人才评估及甄选应具有的监督、调控、导向等功能,该指标体系的构建遵循以下原则:一是可操作性和可比性原则,二是科学性和先进性原则,三是系统性和全面性原则[12]。
该指标体系以人才的基本素质、工作业绩、科研成果、科研项目为一级指标。根据电力企业内高端人才综合能力评价指标的重要程度,给定各一级指标所占比重如表1。

表1 一级指标比重
每个一级指标由若干二级指标组成,共14个二级指标,每个二级指标所占权重可以由该领域的相关专家提供参考意见来确定。二级指标下可设立多个不同权重的考察项为三级指标,如二级指标职称下设置三级指标为正高级、副高级、中级、初级等。给定一级指标为θi,二级指标为θij,三级指标为θijk,通过对每个样本的三级指标θijk进行评测来得出二级指标θij的得分,各二级指标θij得分累加得出一级指标θi的最终得分。
1.2 数据标准化处理
选取电力企业100名典型人员为研究对象,以各项指标数据为基础,对其科研综合能力进行评价、甄选。实验样本中的各项定性指标由电气领域相关专家评定,其赋值可根据企业自身的要求改变。部分典型样本数据如表2所示。
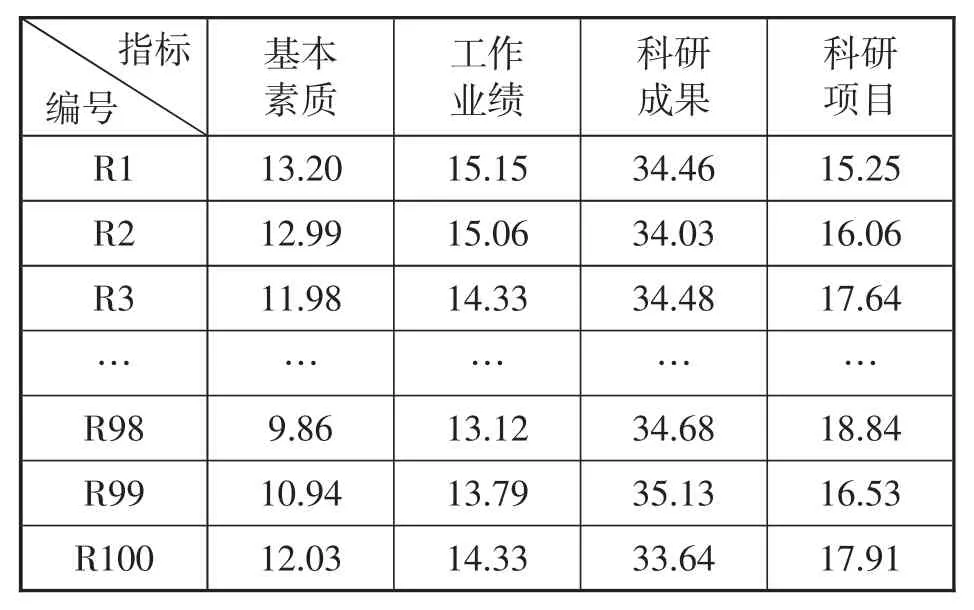
表2 部分样本数据
设论域 X={x1,x2,…,xn}为被甄选的对象,每个元素xi由m个数据表示,对第i个元素有:
这种青霉与匍枝根霉的模型易于制作和演示,可以引起学生的学习兴趣,更重要的是可以将肉眼难以辨别的微观结构放大,突出展示教学要求学生掌握的结构特征,有助于学生掌握两种真菌的结构特点以及两者的区别。这种模型还可以由学生自己制作完成,既能加深学生对真菌结构特点的理解,又能培养学生的观察能力和动手能力,在实际教学中获得了较好的效果。
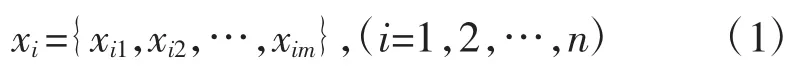
得到原始数据矩阵为:

在实际操作中,不同维度数据有着不同量纲,为了对不同量纲间的数据进行比较,应对各个评价指标数据做出适当的变换,消除量纲影响。即对其做标准化处理,本文采用极差变换:

其中,xik样本指标数据;i=1,2,…,n;k=1,2,…,m。部分极差变换后的样本数据如表3所示:
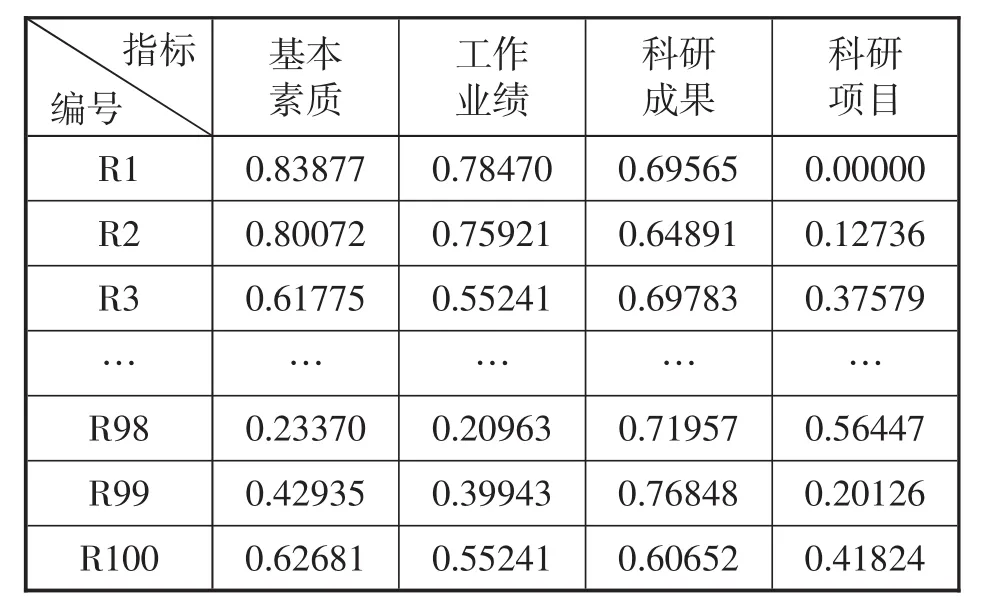
表3 部分极差变换后的样本数据
2 人才甄选方法及实现
2.1 FCM 算法原理
聚类,就是将数据集按照某个特定标准分割成不同的类或簇,使得同一个簇内数据对象的相似性尽可能大,不在同一个簇内数据对象的差异性也尽可能地大。传统的聚类算法K-means是一种硬性聚类方法,有着“非此即彼”的性质,其结果只有1和0两种。由于其硬性划分特性,导致聚类灵活性欠佳。
FCM类型的算法最早是从“硬”聚类目标函数的优化中导出[13],在 1981 年由 Bezdek 首次实现[14]。该算法将硬性聚类算法推广到模糊情形,不会强制把几个类边界上的对象完全分配到其中一个类。而是为其分配大小介于0与1之间的隶属度,以指示它们的部分隶属度关系。与K-means相比具有一定的灵活性,更适合于人才甄选问题。
FCM算法把聚类问题转化为非线性的数学规划问题,目标函数J及约束条件如下:
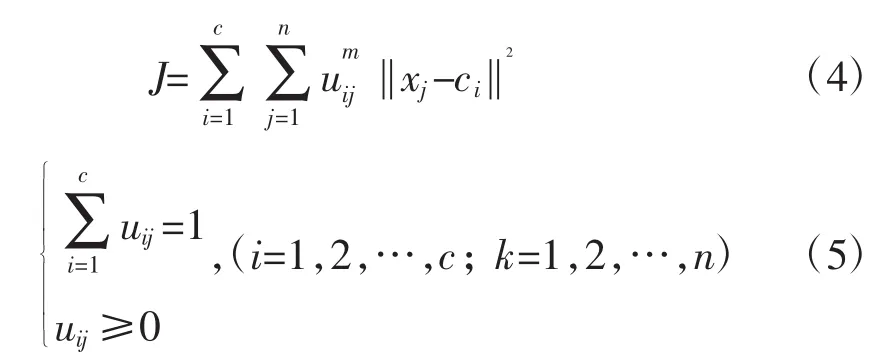
其中,J由样本到聚类中心的距离与该样本的隶属度相乘组成;c为聚类个数;n为样本数;m为模糊加权指数;uij为隶属度;xj为样本点;ci为聚类中心。
隶属度及聚类中心的更新如下:
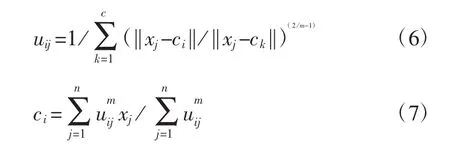
隶属度矩阵U为:
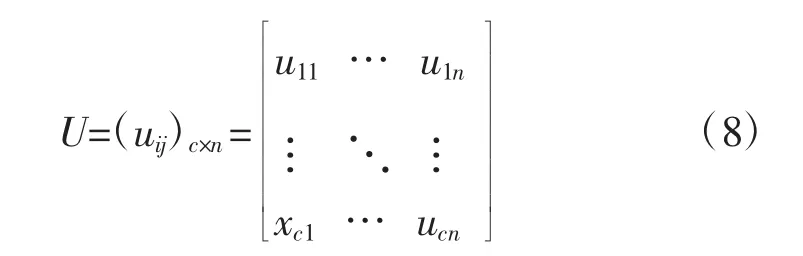
FCM算法运行时,需要建立模糊相似矩阵,也称之为标定。本文FCM算法采用欧氏距离来建立模糊相似矩阵。
FCM算法实现的具体流程如图2所示。

图2 FCM算法流程图
2.2 确定最佳聚类簇数
聚类性能度量也称为聚类的有效性指标,用来评估聚类结果的好坏[15]。使用FCM将样本数据进行分析后,人才被分配到c个簇中,簇的有效性决定了人才甄选结果的可靠性。而簇有效性的度量一般基于簇内和簇间两方面,理想的聚类效果应具有最小的簇内距离和最大的簇间距离[16]。轮廓系数(Silhouette Coefficient)结合了凝聚度和分离度,用于评估聚类的效果,以此来确定最佳聚类簇数。簇中每个样本点的轮廓系数值计算方式如下:
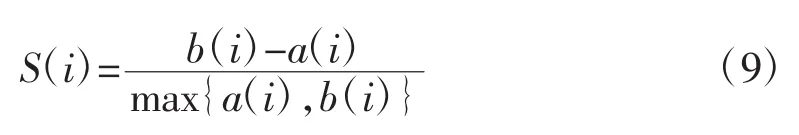
其中,a(i)为样本i到它所属簇中所有其它点的平均距离,体现簇内凝聚度;b(i)为样本i到与它相邻最近的一簇内所有点的平均距离,体现簇间分离度。
轮廓系数 S(i)∈[-1,1],其值越接近 1,表明样本i越适合该类,反之,越接近-1,表明样本i越不适合该类,更应该被分配到其他簇。当S(i)接近于0时,样本i位于两个簇的边界。
为实现不同能力层次的人才甄选,对其能力有一个清晰界定。本文将聚类簇数c设置为4、5、6进行试验,得出轮廓系数如下图3、图4、图5所示,横坐标为轮廓系数,纵坐标为聚类数。
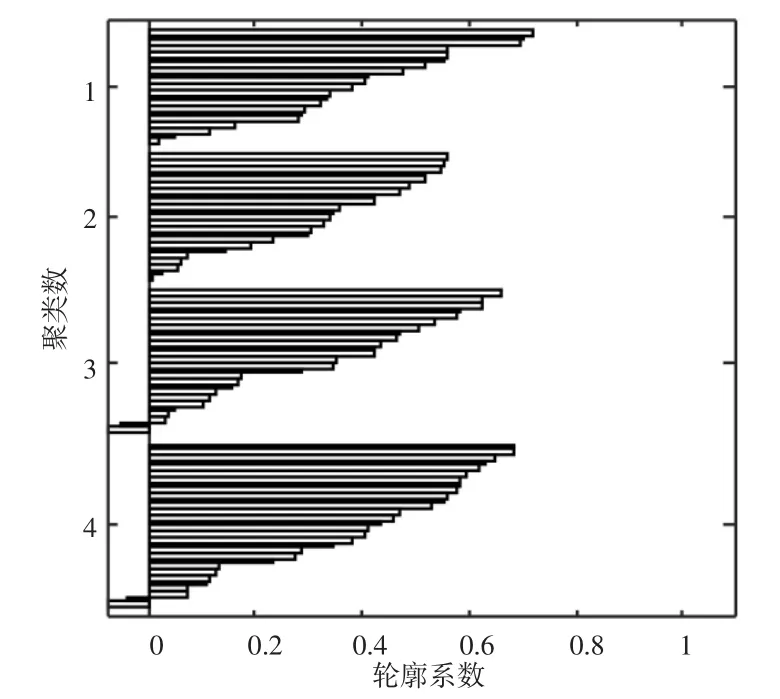
图3 聚类数为4时轮廓系数图
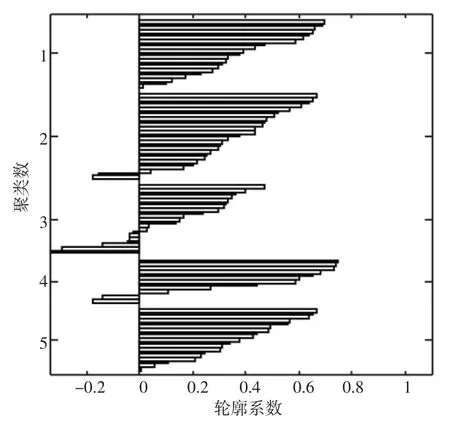
图4 聚类数为5时轮廓系数图
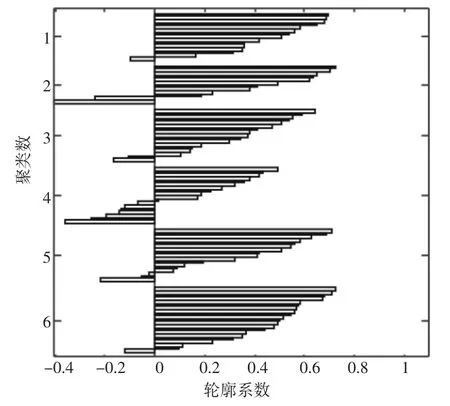
图5 聚类数为6时轮廓系数图
图3表示聚类数为4时轮廓系数值的分布情况,图中每一条矩形代表一个样本的轮廓系数值。100组样本数据在FCM算法下分为四类,轮廓系数值大于0的样本有96组且大部分值大于0.4,表明人才甄选结果有效性较高。小于0的样本有4组,少数样本值接近于0,表明误差较小。聚类簇数为4时,整体甄选效果较好。
图4表示聚类数为5时轮廓系数值的分布情况。类别1和类别5效果较好,类别2、类别3、类别4有个别样本轮廓系数值小于0,存在分配误差。类别3共21组样本,7组样本分配存在误差,甄选效果较差。因此,簇数为5时,总体甄选效果一般。
图5表示聚类数为6时轮廓系数值的分布情况,从图中可以观察到所有簇中都出现了样本分配误差。其中类别4的簇内共18组样本,出现误差的样本有7组,误差最大,整体甄选效果较差。
通过对以上轮廓系数图的分析,确定最佳聚类簇数为4。
3 人才甄选结果分析
设定簇数 c 为 4,迭代停止阈值 eps=1×10-5,给定模糊加权指数m=2。将电力企业内人才各项指标数据X输入,经FCM算法聚类后,其目标函数变化如下图6所示:
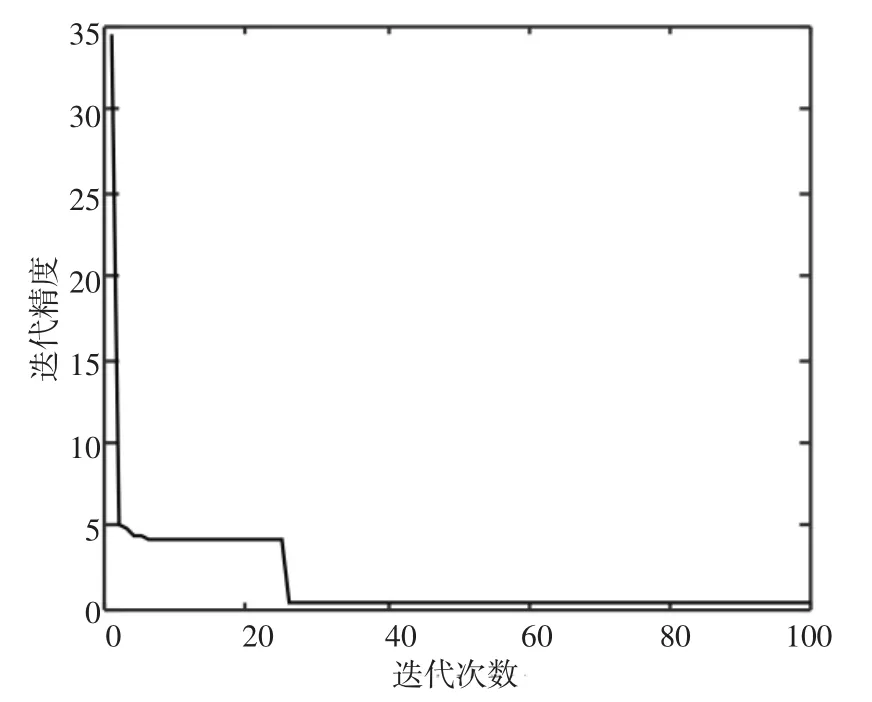
图6 目标函数J变化图
FCM算法是使目标函数最小化的迭代过程,其优化过程如图6所示。样本数据经过FCM聚类,在第5次迭代后陷入局部极小值。第6~22次的迭代过程中,寻求跳出局部极小值点,直到第23次迭代时跳出。此时,目标函数J满足迭代停止阈值,达到最优,人才按不同能力层次被分为4类。人才甄选结果散点图如图7所示:
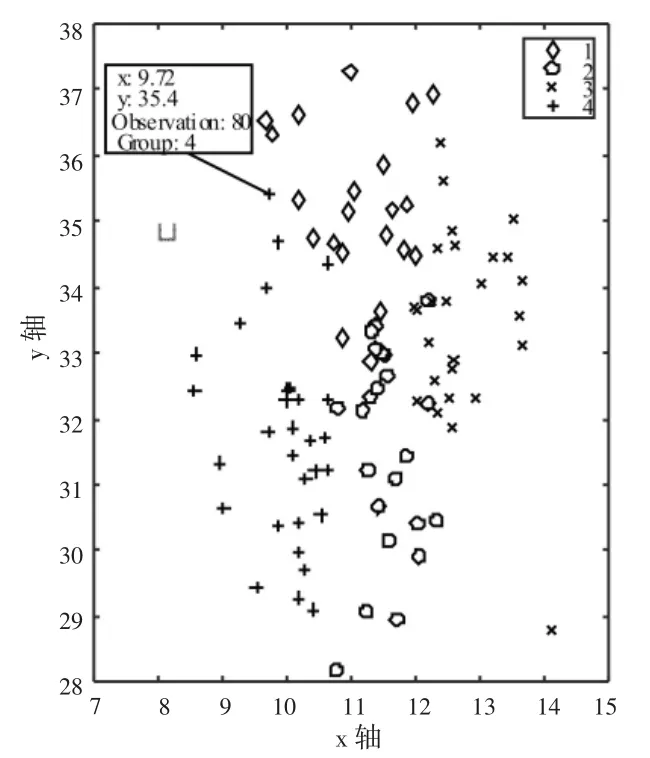
图7 人才甄选结果散点图
在图7中,可直观看出各个数据样本经FCM算法聚类后的分布情况,每种图形代表着一个簇中的所有样本。如图中所标注样本点,其代表第80个样本点,属于第4个簇,在二维空间中的分布为(9.72,35.4)。
由于本文采用FCM算法是基于欧氏距离的,所以其分类依据为样本到聚类中心的距离大小。部分人才甄选结果如下表4所示:
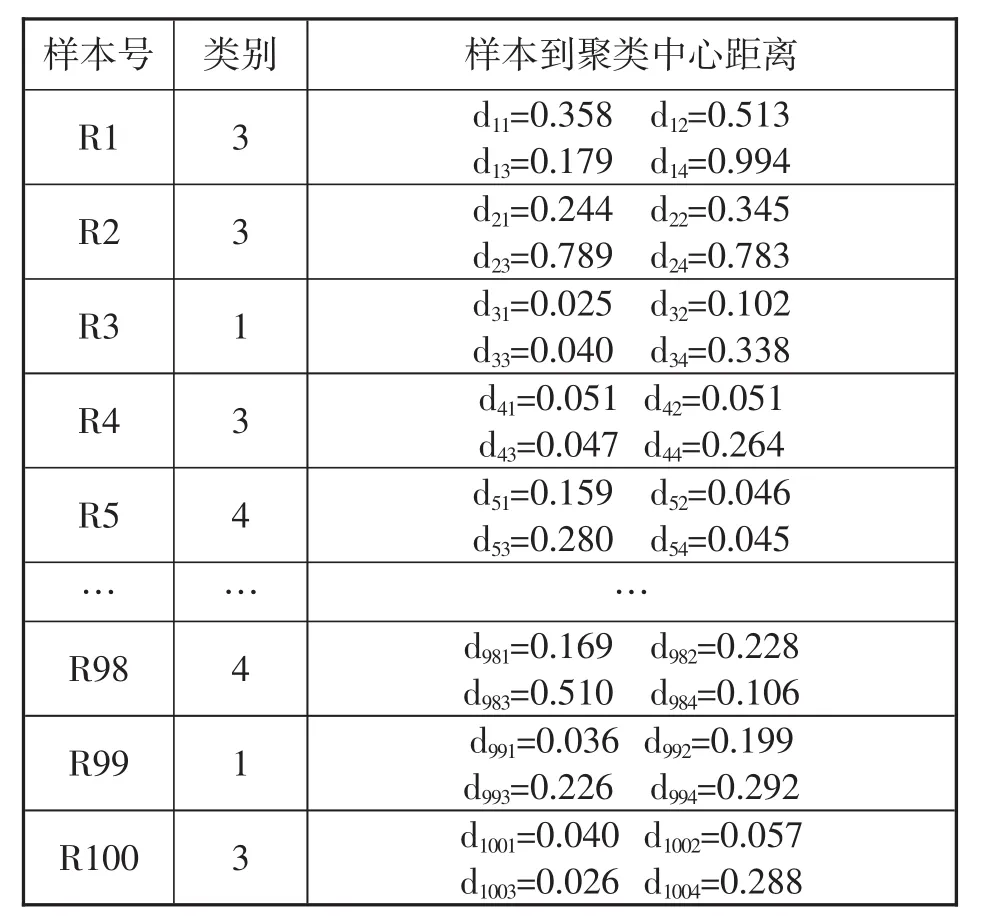
表4 部分人才甄选结果
样本点距离聚类中心的距离越小,表明样本点越应归为该类。如样本R1距离聚类中心3距离最近,归为类别3,样本R3距离聚类中心1距离最近,归为类别1。全部样本的甄选结果由表5给出。
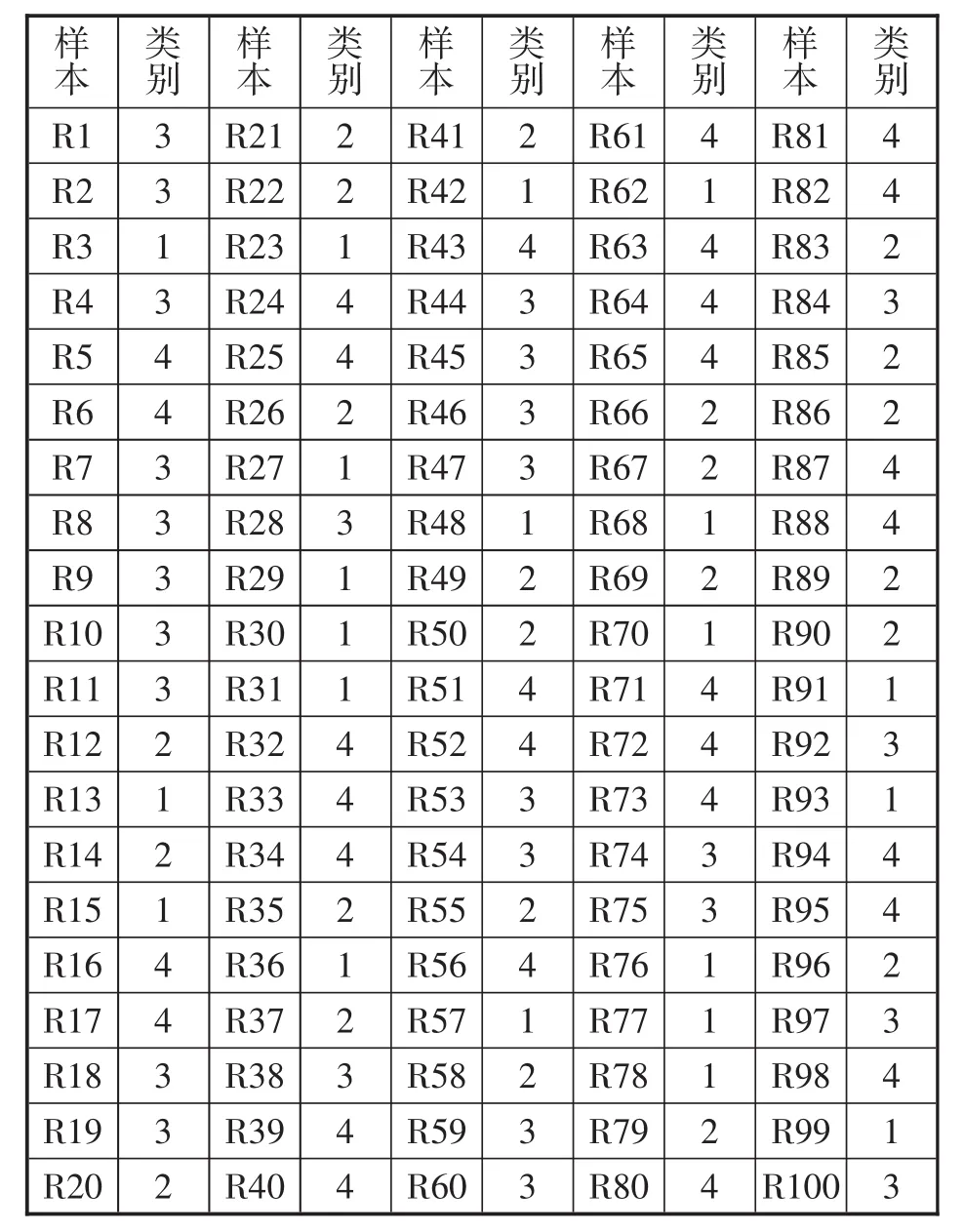
表5 甄选结果
在FCM算法下,对电力企业高端人才的各项指标数据进行客观分析,使其综合能力得到有效界定。最终,人才被分为4类,分别定义为A型人才、B型人才、C型人才和D型人才,实现人才甄选目的。
4 结束语
通过FCM算法,对样本不同维度的数据按其内部联系进行分析,聚类结果反映出电力企业人才的不同能力层次,达到人才甄选的目的。其中,对数据做极差变换,可消除量纲对实验结果的影响。利用轮廓系数法确定最佳聚类簇数,可提高聚类结果的有效性。将FCM算法引入高端人才甄选,可减少人为分类的主观性因素影响,解决人工统计分析的局限性问题。同时,可处理大量高维非线性样本数据,改善传统K-means算法的硬性划分特性,使人才甄选更加灵活、客观。

