行星着陆动力下降轨迹优化的中心差分凸化方法

李明翔，泮斌峰

（1.西北工业大学 航天学院，西安 710072；2.航天飞行动力学技术国家级重点实验室，西安 710072）

引 言

行星探测是人类探索太空最重要的途径之一，月球和火星探测是当前行星探测的热点。当目标行星大气比较稀薄或者没有大气时，探测器将无法使用降落伞降至安全速度，基于反推火箭的动力下降成为实现行星表面软着陆的一种重要手段。由于行星动力下降过程存在诸多不确定性因素，其在线轨迹优化是实现探测器安全、精确着陆所需要解决的重要问题。

近年来，序列凸优化方法成为求解上述在线轨迹优化的有效手段[1-2]，其本质是将无限维空间中的最优控制问题通过离散转化为有限维空间中的非线性规划问题，并利用序列凸优化理论通过凸化处理后迭代求解。Szmuk等[3]通过引入虚拟控制量并且在动力学方程中定义了新的时间状态量，提出了一种终端时间自由的序列凸优化方法计算框架，能够较好地得到最优燃料轨迹；其不足之处是对初始猜想敏感且迭代次数多。Blackmore等[4]通过将燃料最优问题凸化为二阶锥规划（Second-Order-Cone-Programming，SOCP）问题，并考虑了坡度约束，能够较快求解出燃料最优的下降轨迹。上述方法对于终端时间固定的情况能够得到较好的解，但由于其终端时间采用线性搜索方法计算，效率较低。此外，Liu等[5]考虑了气动力作用下的一级火箭回收问题，通过无损凸化技术和动力学方程归一化提高了算法收敛性和快速性。该方法在凸化过程中重定义了控制量，公式推导复杂且引入了额外的约束和计算量，只能处理固定终端时间问题。

有别于上述研究方法，本文探索使用预标记中心差分替代解析表达式计算动力学矩阵，并对动力学方程采用直接线性化替代变量代换后再线性化的凸化方法，最后研究行星动力下降燃料最优控制问题中近似最优终端时间的确定方法，以提高序列凸优化在线轨迹优化方法的工程实用性。

1 行星动力下降轨迹优化问题建模

以着陆点为原点建立空间直角坐标系，着陆点一般不直接选在地表，而是距离地面稍有一定距离，方便提供安全缓冲余量。x轴方向预先约定，z轴垂直于地表向上，y轴满足右手螺旋关系。行星动力下降可以表述为经典的Bolza型最优控制问题

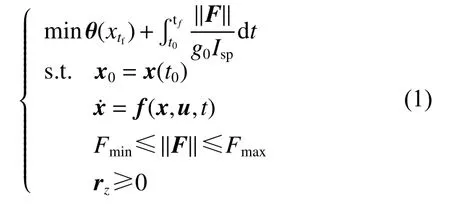
其中终端性能指标为

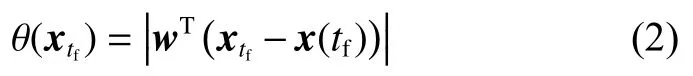
式（1）中约束分别为初值约束、动力学约束、控制量幅值约束和防撞约束，其中反推发动机为了避免多次开关机带来的可靠性问题，在实际工作中一般不将其完全关闭，故需限定最小推力。行星动力下降动力学方程为

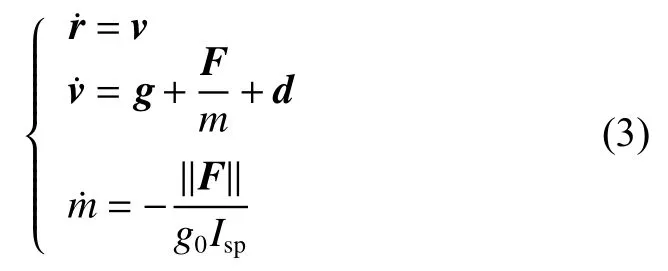
其中：g=[00–g（rz）]T是行星的重力加速度矢量。

考虑到动力下降段高度在2～5 km之间，高度相比行星半径尺度较小，重力加速度变化也较小，可以直接通过海拔高度计算。本文以火星引力场为例，其表面重力加速度为gM=0.377、gE=3.7 m/s2、RM=3 397 km，距地表任意高度的重力加速度为

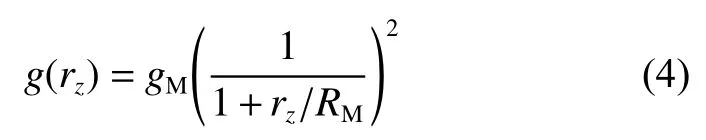
此外，d=[dxdydz]T是3个方向的气动加速度，分为可建模的气动（如飞行器的气动阻力）和无法建模的随机风场扰动。由于火星大气较为复杂，不适合在在线轨迹优化中应用[1]，因此本文采用文献[3～4]的处理方式，在动力下降段中以忽略气动力作用下简化的动力学进行分析，气动扰动可以通过后期设计控制器加以克服[6]。

2 序列凸优化问题建立

2.1 控制量凸化

采用直接法求解优化问题式（1）时，需要先将其离散到有限维空间中。当终端时间tf确定时，将飞行时间[0，tf]等距离散为N个时刻，即N–1个子区间，并在这N个时刻对状态量和控制量进行离散，方便施加过程约束。

对于控制力幅值约束

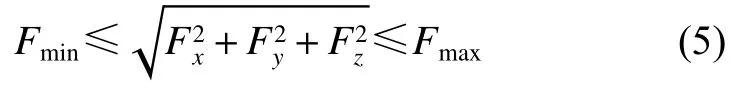
因最小推力幅值约束是二阶锥补集，为将非凸约束式（5）凸化，在各个离散点处引入推力松弛因子Fη

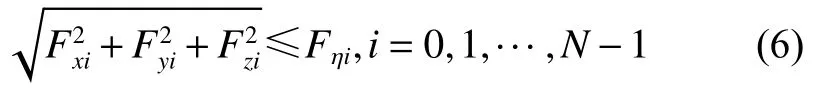
此时，控制幅值约束可以表示为

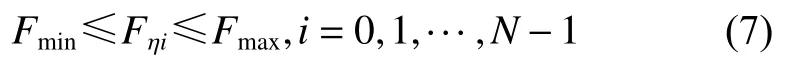
至此非凸约束式（5）被等价转换为凸约束式（6）和式（7），积分型性能指标也可以表达为关于Fη的线性组合

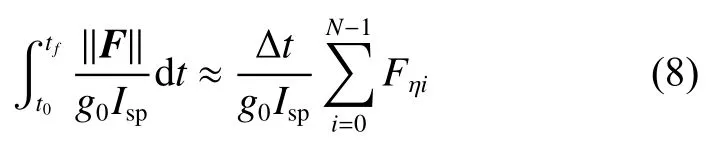
其中：Δt=（tf–t0）/（N–1），即使用矩形公式将积分化为求和。

2.2 中心差分法改进动力学凸化

为将非线性动力学微分方程约束处理为凸约束，需进行凸化处理。文献[5]和文献[7]中处理上述动力学方程通常使用2种凸化技巧：将推力矢量分解为推力大小和方向余弦、对质量取对数重定义新的状态量。前者存在的问题是，方向余弦约束为非凸等式约束，虽然文献[3]中通过极小值原理证明其可无损转化为凸锥约束，但实际数值求解中经常出现不稳定因素，造成收敛速度较慢，且控制变量从原来的3维上升到4维，问题复杂度上升。后者对质量取对数后重定义新的状态量，再对推力约束进行一阶泰勒展开线性化和直接对动力学泰勒展开线性化，本质上都是线性化，并未降低原问题的非线性，仅将非线性从动力学方程转移到过程约束中。取对数后推力不等式约束中存在指数函数，相比原来仅含加、乘法的公式增加了计算量，且人为增加了推导公式和编程的工作量。

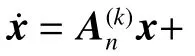
对于动力学矩阵A、B、C的分量使用差分直接计算，第i个微分方程，对第n个离散点处的状态量（控制量）的第j个分量的偏导的差分计算公式为

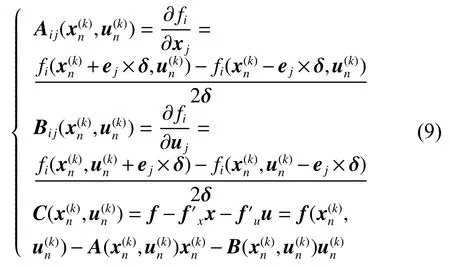
为了消除不必要的计算量，在设计程序时，提前对每个动力学微分方程显含的状态量和控制量索引进行标注，仅计算这些位置的偏导数，其余元素直接赋值为0。将式（1）中的微分方程约束转换为线性代数方程约束，为表示方便，简记为

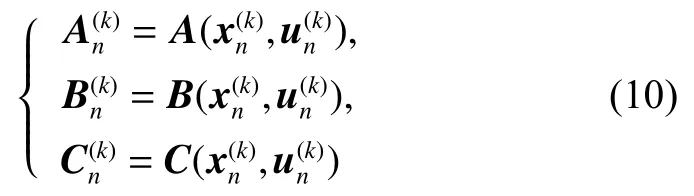
为兼顾计算精度和计算效率，使用梯形法施加动力学约束

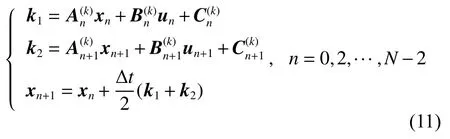
启动第一次迭代时，动力学矩阵A，B，C的计算需要提供k=0时每个离散点n处的状态量x（0）和控制量u（0），即初始猜想。对于状态量，如果同时存在初值约束和终端约束，则状态量的初始猜想直接设计为两个状态的线性插值

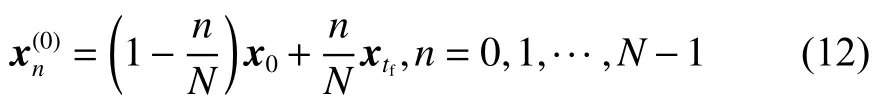
如果仅存在初值约束（如质量m），则状态量初始猜想设计为常值向量

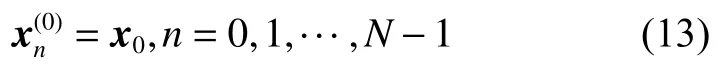
对于控制量，初始猜测全部初始化为0，即

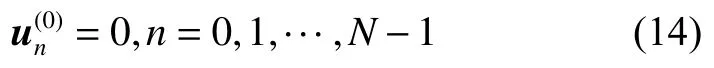
式（12）～（14）简洁的设计过程直接消除了利用数值积分设计的轨迹引入的人为因素和计算量，虽然初始猜想并不符合动力学方程约束，但在每次迭代求解后得到的轨迹将完全满足动力学约束，并在不断迭代中使轨迹收敛到最优解。

3 数值仿真

3.1 固定终端时间算例仿真

为验证前文所设计算法的有效性，给定飞行状态和航天器参数如表1所示，求解行星动力下降段燃料最优的轨迹优化问题。

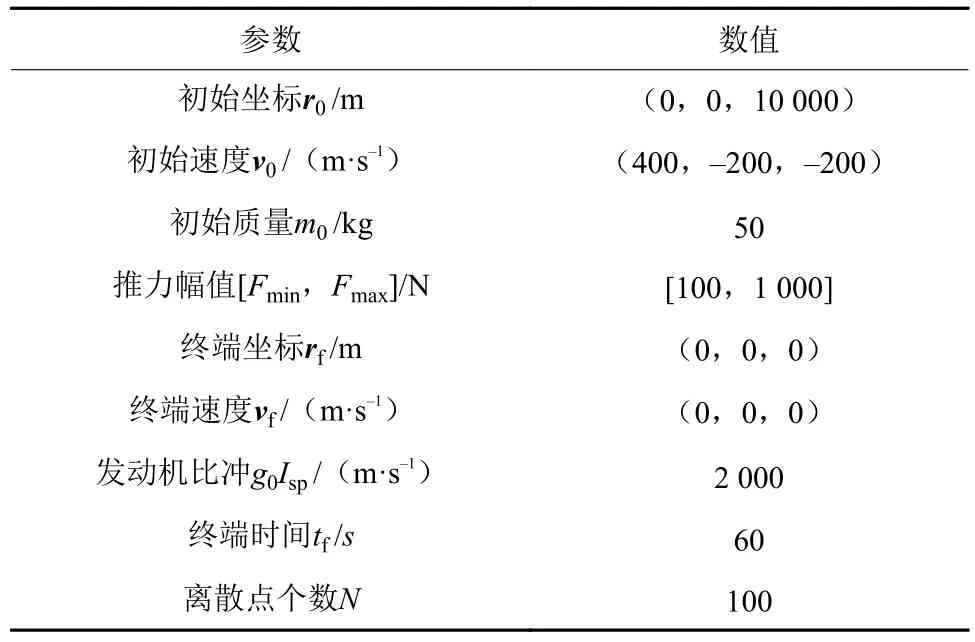
表1 仿真设定参数Table 1 Simulation parameters

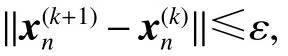
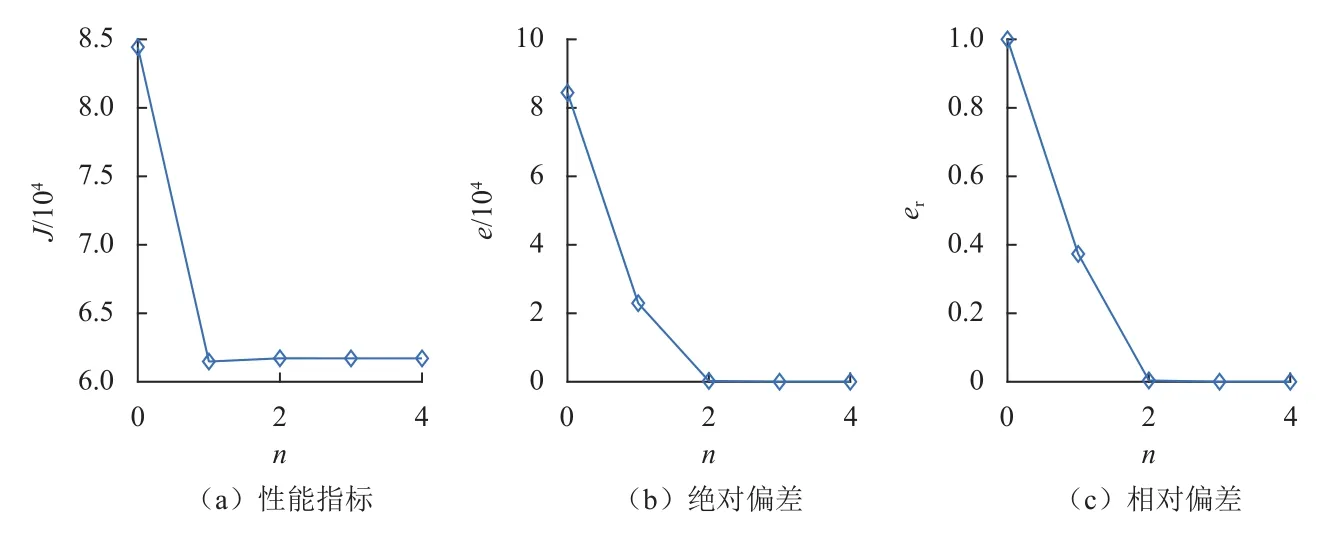
图1 性能指标及其绝对偏差和相对偏差随迭代次数变化图Fig.1 Performance index and its absolute deviation，relative deviation versus iterations

本文采用C++调用SOCP求解器ECOS[9]进行求解。计算环境建立在CPU为i5-8300H（基频2.2 GHz，睿频3.8 GHz）Windows系统的PC上，耗时统计从进入main函数开始到满足序列凸优化迭代条件er＜ 1%退出为止（不含优化结果输出时间），求解500次，均为迭代3步收敛，耗时统计如图2所示，平均耗时0.130 1 s，优化所得控制量与状态量如图3～6所示。

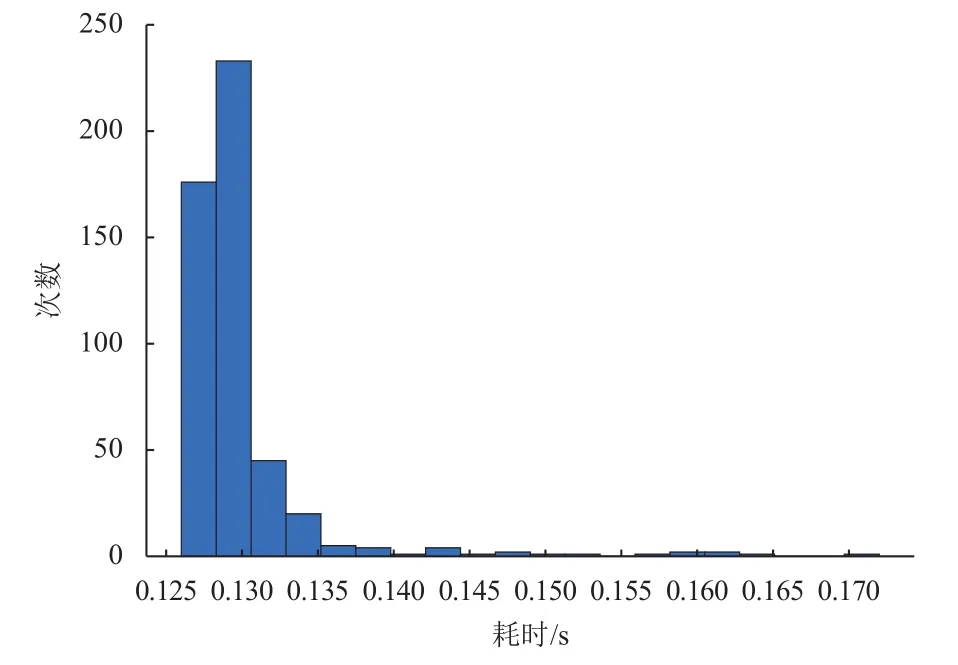
图2 求解表1算例500次耗时统计Fig.2 Computing time statistic of solving the case in Table 1 500 times

优化得到的推力曲线如图3所示，可以看到推力幅值被精确地约束在[100，1 000]N的区间内，表现为bang-bang控制。速度曲线如图4所示，可看到终端速度被精确约束在0 m/s，图5中质量曲线m（t）的导数是控制力幅值函数||F（t）||2，可以看到m（t）随||F（t）||2也相应分为3段。

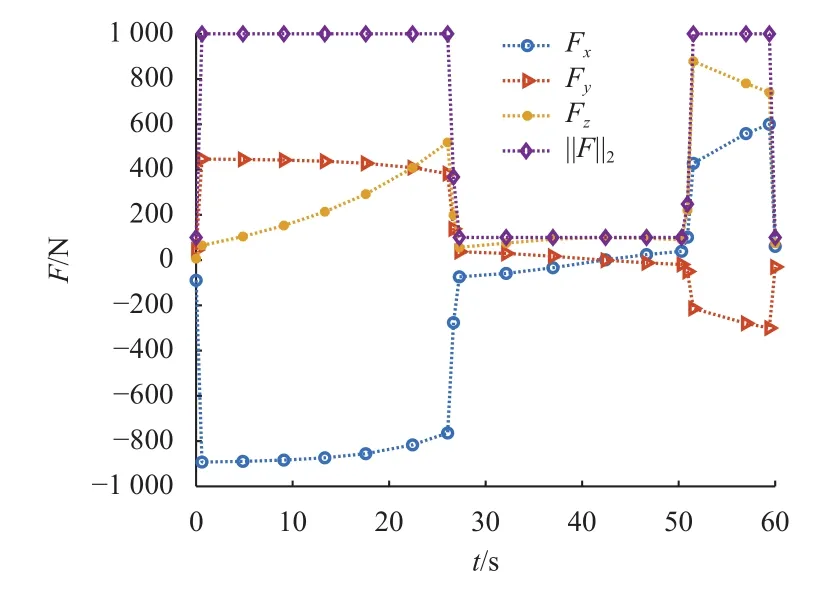
图3 发动机3个方向推力曲线Fig.3 Thrust component in three directions

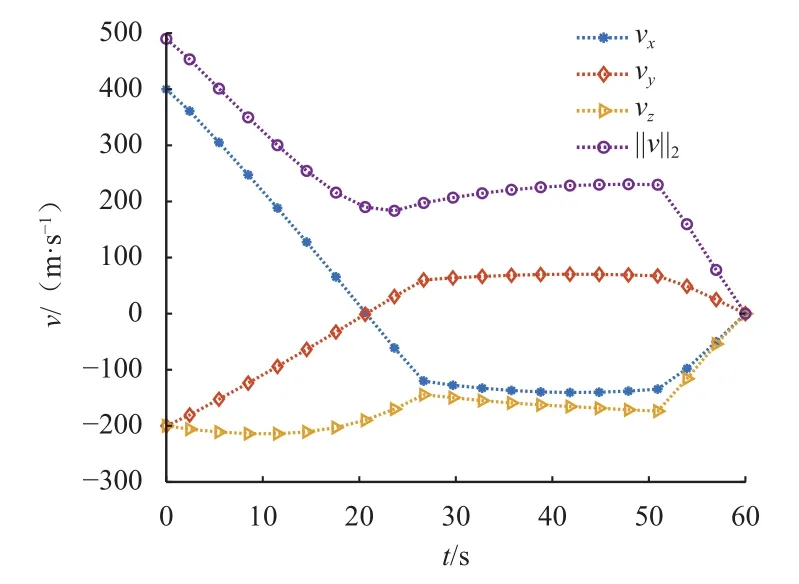
图4 飞行器速度曲线Fig.4 Velocity profiles of optimal trajectory

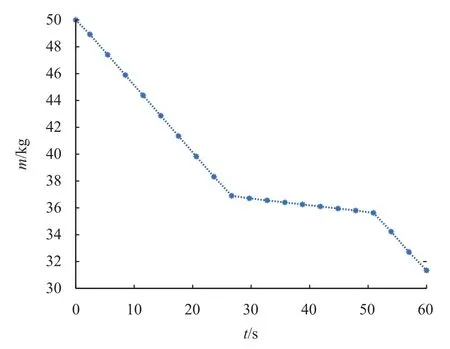
图5 飞行器质量曲线Fig.5 Mass profile of optimal trajectory.

图1证明了用中心差分法建立序列凸优化模型的有效性，良好收敛性和对初始猜测弱敏感性，事实上由图1还可以看出如果以相对偏差作为性能指标，可认为第3步已经收敛，轨迹随迭代次数变化如图7所示，3～5次迭代产生的轨迹基本重合，算例对应的三维轨迹和各离散点处推力矢量如图8所示。

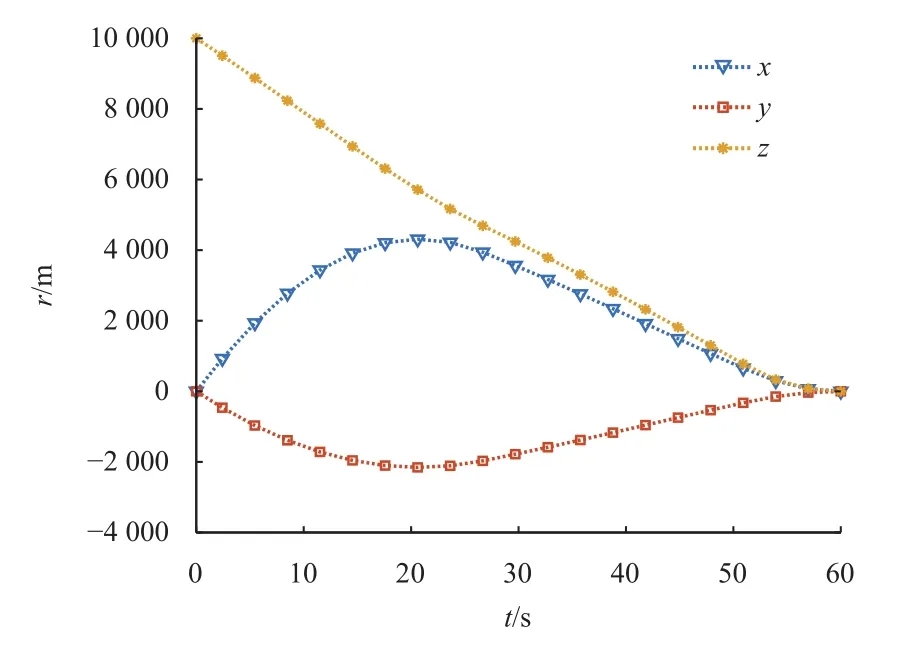
图6 飞行器位置相对于着陆点变化曲线Fig.6 Position profiles of optimal trajectory

图7 tf=60 s轨迹随迭代次数变化Fig.7 Trajectory versus iterations for case of tf=60 s

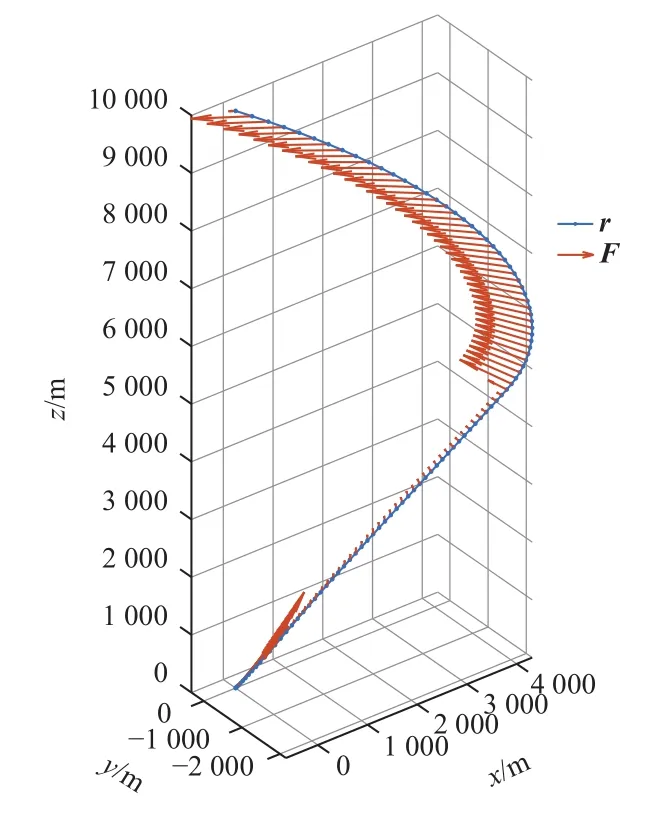
图8 tf=60 s优化轨迹和推力矢量Fig.8 Optimal trajectory and thrust for case oftf=60 s

3.2 最优终端时间计算

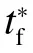
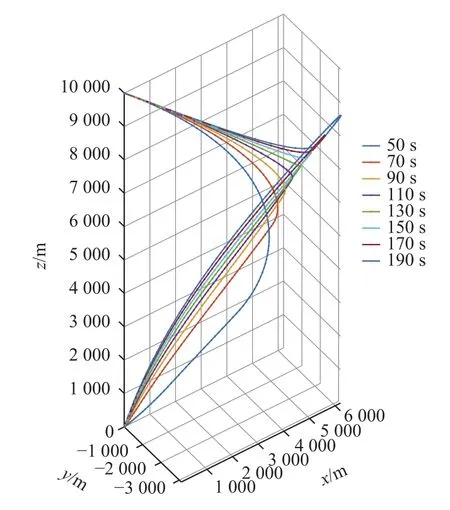
图9 tf∈[50，190]s最优轨迹簇Fig.9 Optimal trajectories attf∈[50，190]s

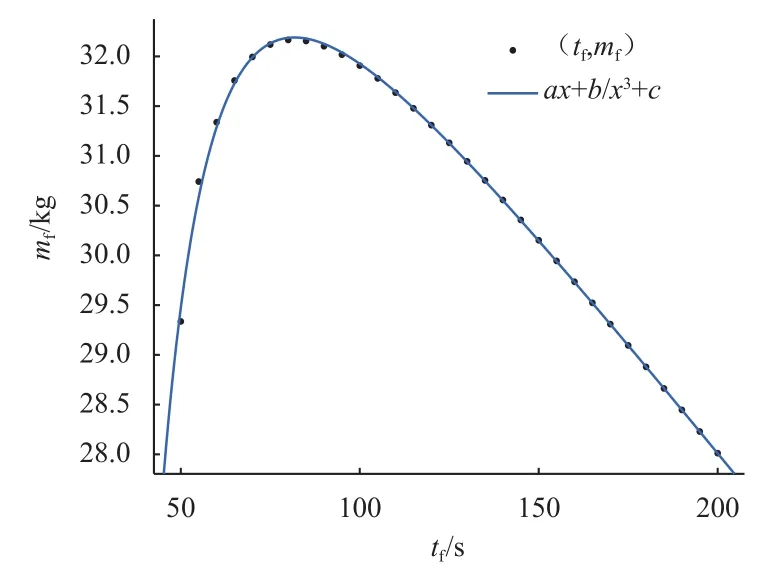
图10 不同tf下最优轨迹对应的剩余燃料质量mfFig.10 mfof optimal trajectories at differenttf

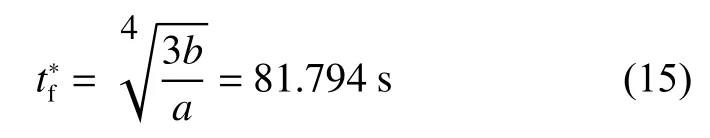
由图11可见，降低离散点个数对最优终端时间的确定几乎不产生影响，但可以显著降低计算量，如图12所示。在实际工程应用中，可以通过降低离散点个数的方式或者使用低精度的动力学约束进行最优控制模型的求解，以快速获取（tf，mf）样本点。样本点个数不能少于3个，使用最小二乘逼近算法得到a、b、c 3个参数，利用式（15）计算出最优终端时间后，再增大离散点个数进行精规划。

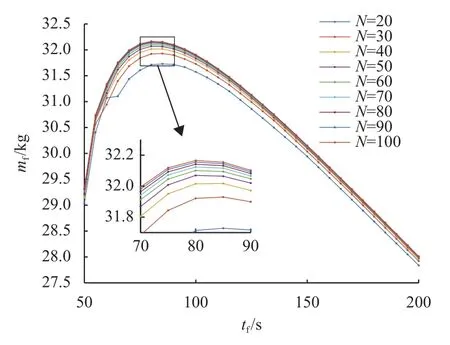
图11 不同离散点个数对应的mf-tf曲线Fig.11 mf-tfcurves under different number of discrete points

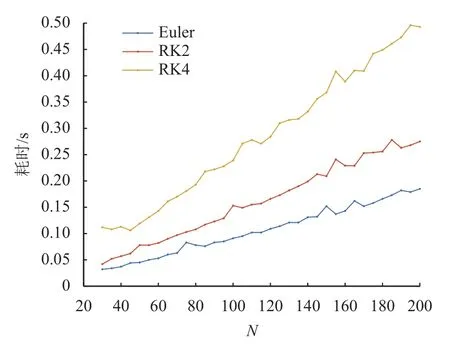
图12 不同离散点个数与动力学约束下的计算耗时Fig.12 Computing time under different dynamics constraint versus discrete points

为验证上述方法的有效性，用计算机随机产生100组初始状态和终端状态，计算出每组条件下的mf-tf曲线，仿真参数如表2所示。仿真结果如图13所示，在100个飞行条件下，除去2个苛刻的飞行情况无解外，其余98个条件下都找到了最优燃料控制的规划轨迹，且有较高的规划成功率。

表2 随机仿真参数设置Table 2 Simulation parameters

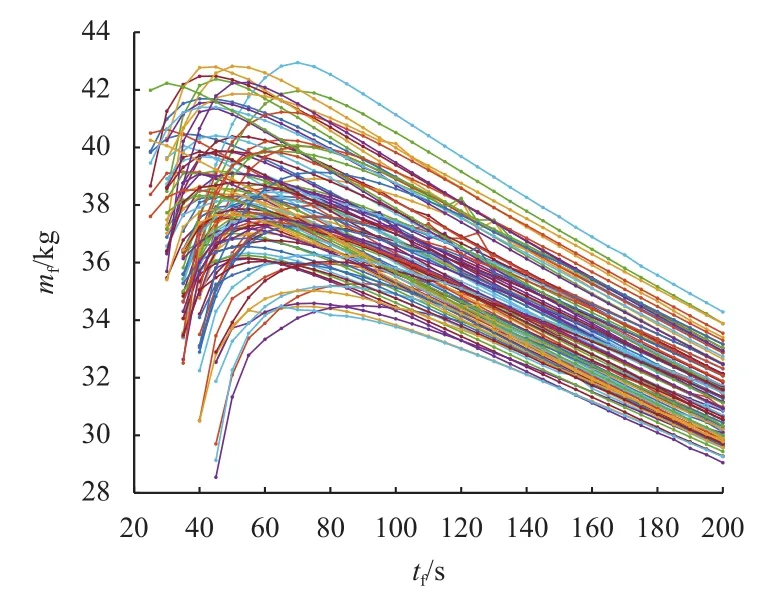
图13 随机初始状态下最优轨迹簇的mf-tf曲线Fig.13 mf-tfcurves of optimal trajectories under random initial state

3.3 算法对比与误差分析

记本文中不对动力学改造直接采用中心差分进行线性化建立的序列凸优化算法为P0，另外两种凸化方法分别为P1[10]和P2[11]

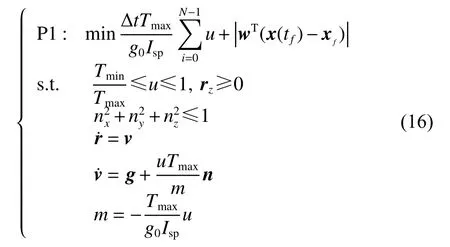
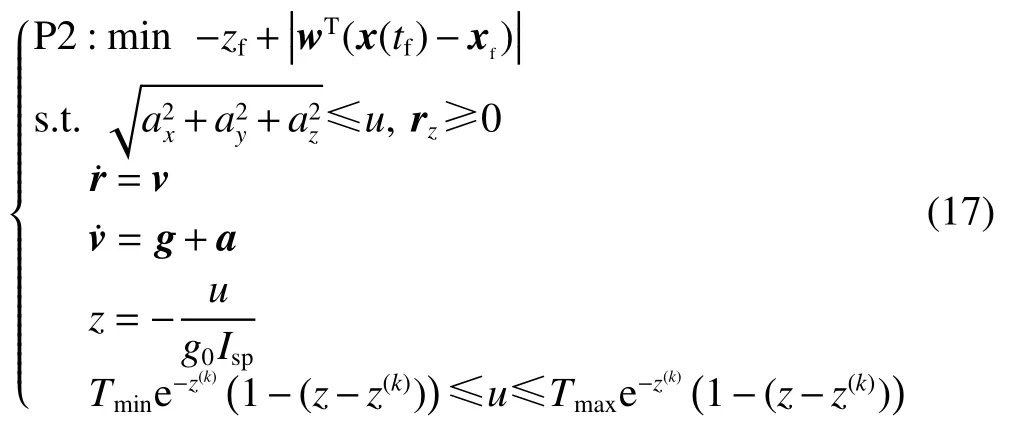
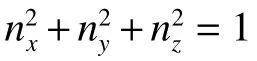
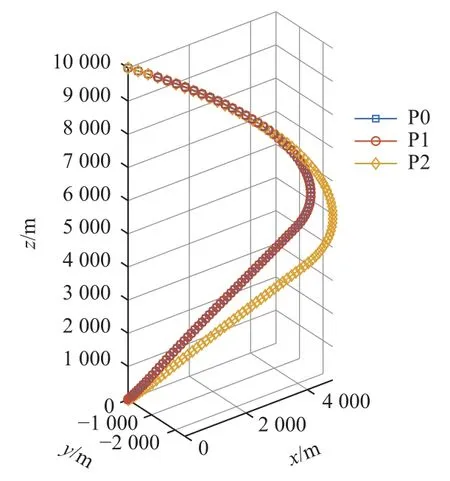
图14 3种凸化方法最优轨迹对比Fig.14 Comparison of optimal trajectories obtained by three convexification methods

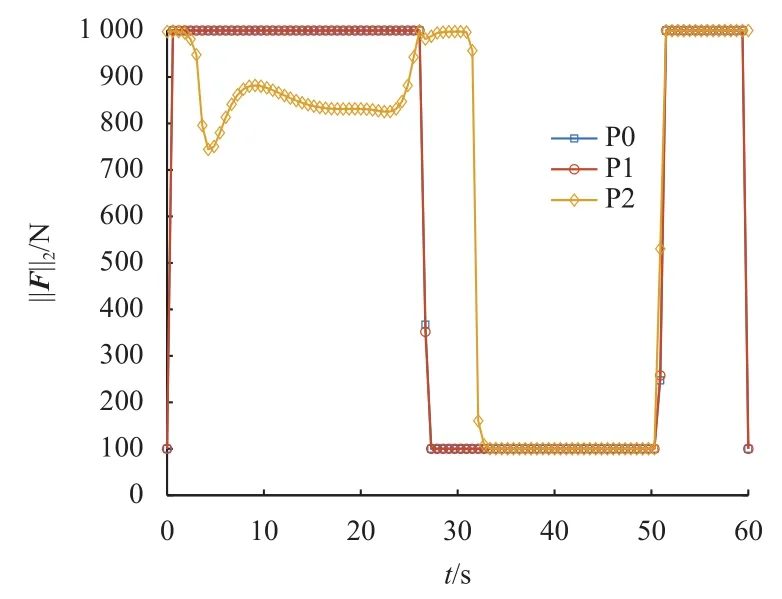
图15 3种凸化方法求解得到的推力幅值曲线对比Fig.15 Comparison of thrust magnitude obtained by three convexification methods

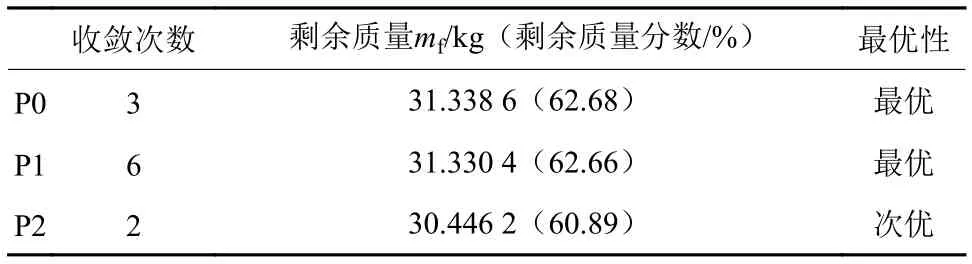
表3 3种凸化方法的计算结果Table 3 Results of three convexification methods

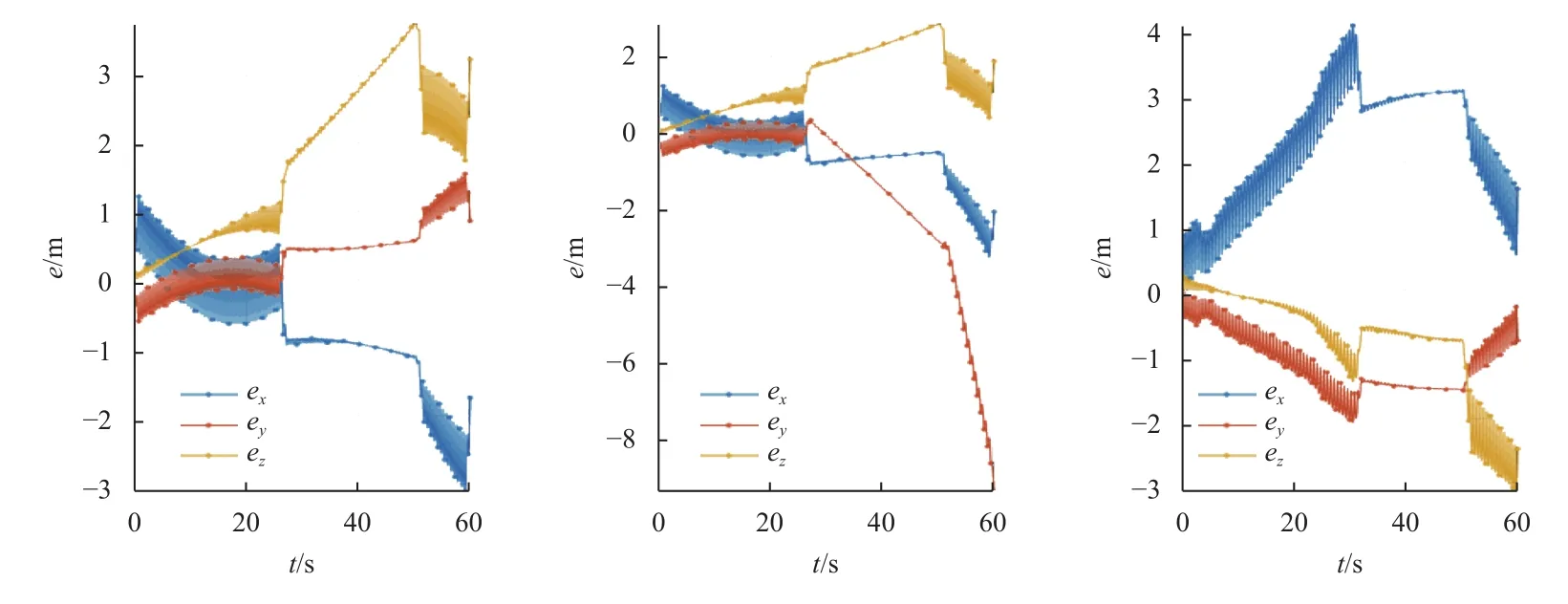
图16 P0、P1、P2求得规划轨迹与积分轨迹的误差随时间变化曲线Fig.16 Error versus time between the integral trajectories and the optimal trajectories obtained by methods P0，P1，P2.

为将非线性动力学模型转化为凸问题进行求解，三者都使用了等距离散的分段线性动力学进行近似逼近，线性化误差和离散误差不可避免。使用控制量积分得到的轨迹和规划所得轨迹进行对比，积分步长为0.01 s。发现3种凸化方式规划解和积分解误差随时间变化都在同一数量级内。

在表4设置的参数下，产生500组随机动力下降任务，分别使用3种方法进行求解，观察终端误差散布。仿真结果如图17～20所示。

表4 终端误差散布仿真参数Table 4 Simulation parameters

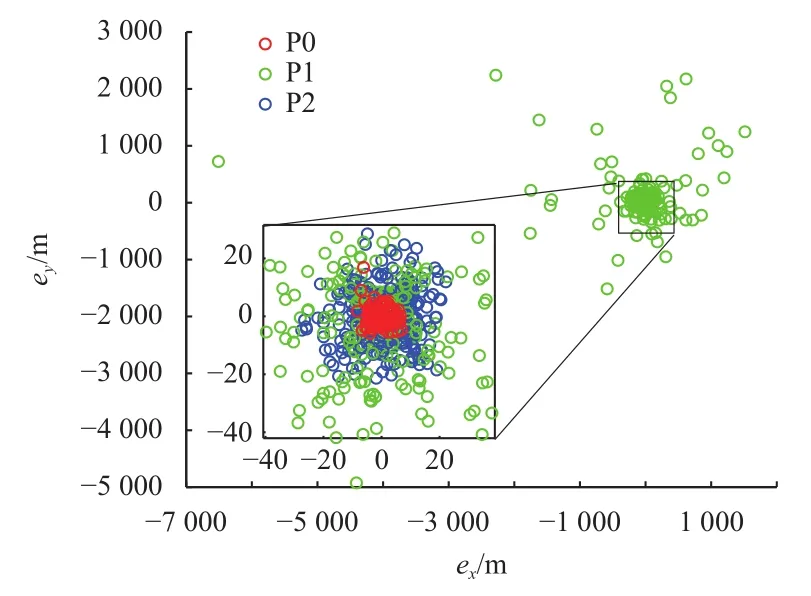
图17 3种方法积分所得终端位置误差散布图Fig.17 Terminal position error of integral trajectories

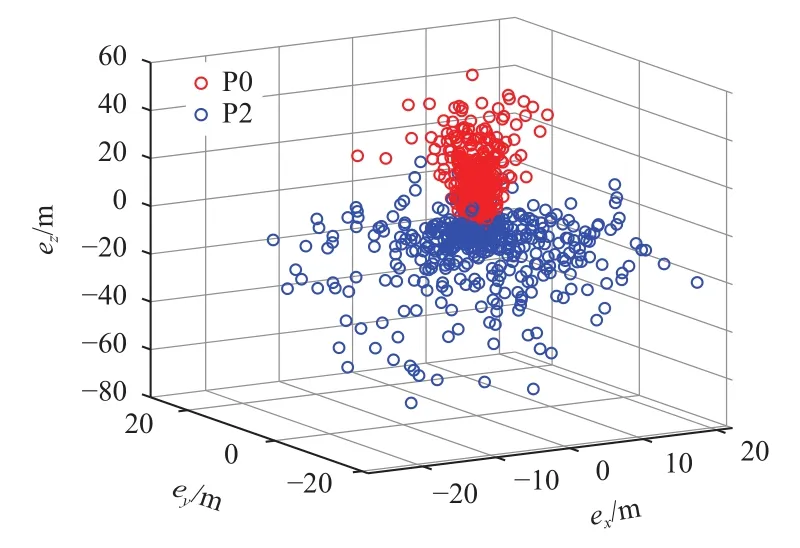
图18 P0和P2积分所得终端位置误差散布图Fig.18 Terminal position error of integral trajectories obtained by convexification methods P0 and P2

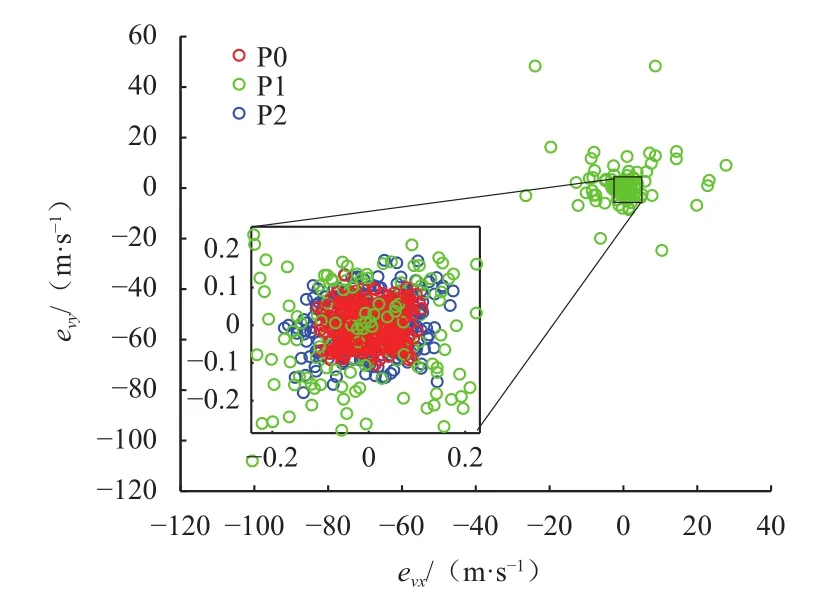
图19 3种方法积分所得终端速度误差散布图Fig.19 Terminal velocity error of integral trajectories obtained by three methods

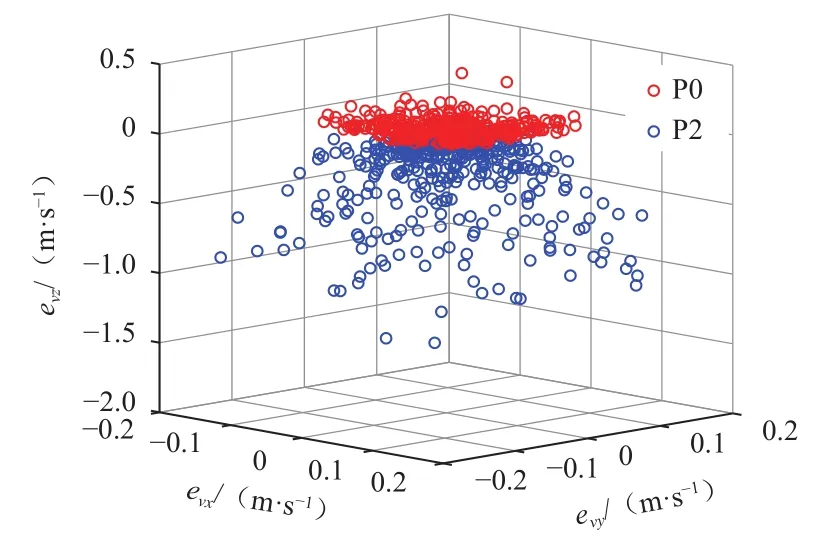
图20 P0和P2积分所得终端位置误差散布图Fig.20 Terminal velocity error of integral trajectories obtained by convexification methods P0 and P2

根据对比，可以发现P1方法的数值稳定性较差，部分算例达到最大迭代次数20次后仍然没有收敛，导致终端误差较大，P0和P2方法终端误差数量级接近。P0相比于P2的位置终端误差散布更加集中，且速度终端误差在z方向上更小。

另外，离散步长对终端误差也都有一定影响。以P0为例，计算表1任务在不同离散点个数下得到的规划轨迹，并通过积分得到终端误差如图21和图22所示。可以看到，终端误差随离散点个数的增加而不断减少。

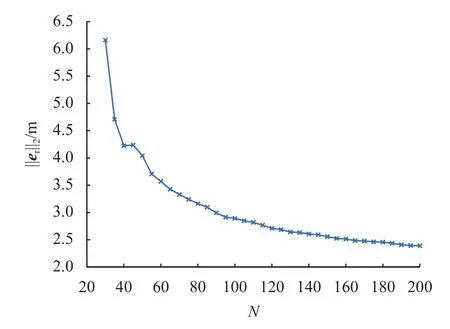
图21 积分得到终端位置误差随离散点个数变化图Fig.21 Terminal position error of integral trajectory versus the number of discrete points

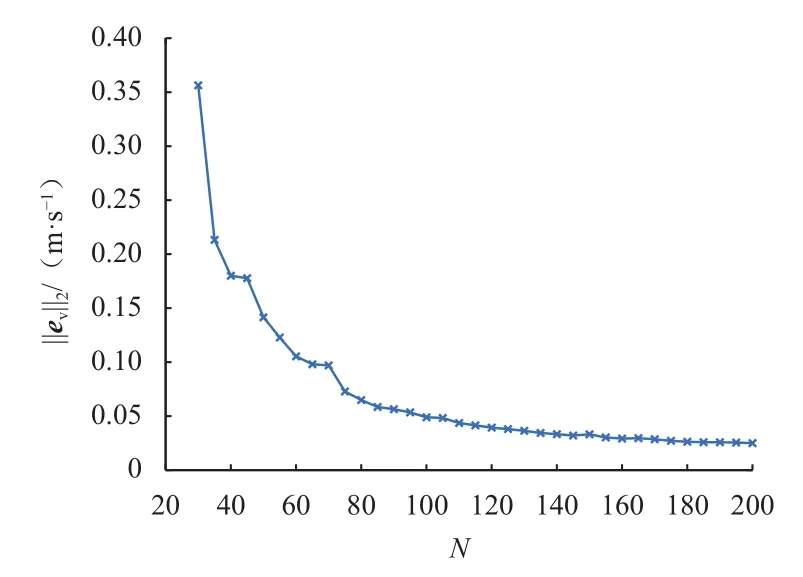
图22 积分得到终端速度误差随离散点个数变化图Fig.22 Terminal velocity error of integral trajectory versus the number of discrete points

固定离散点个数，针对表5设置的随机参数，采用P0在不同终端时间下各打靶200次，如图23和图24所示，积分所得终端误差散布也处于可接受范围内。

图23 不同固定终端时间下积分所得终端位移误差三维散布图及xy平面图Fig.23 3D and projection on xy plane of terminal position error dispersion of integral trajectories at different fixed terminal times

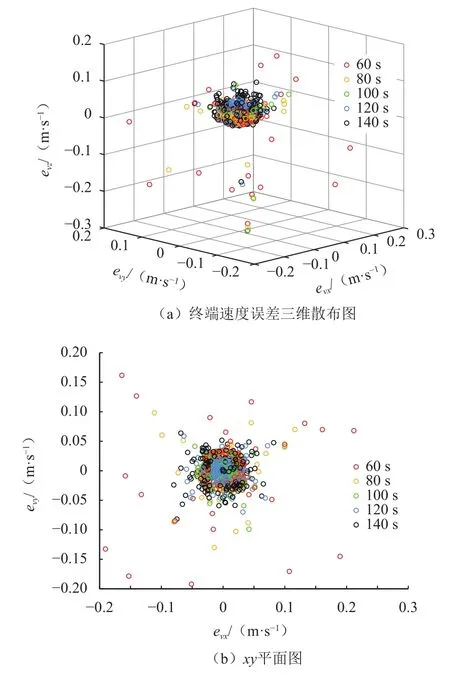
图24 不同固定终端时间下积分所得终端速度误差三维散布图及xy平面图Fig.24 3D and projection on XY plane of terminal velocity error dispersion of integral trajectories at different fixed terminal times

表5 终端误差散布仿真参数Table 5 Simulation parameters

对于收敛性，200个随机初始状态中，P0、P1都求出198个解（第43和181个失败），P2求出199个解（第43个失败），三者收敛性无显著差别。两任务的初始速度大，高度低，规划也失败属于合理现象。虽然第181个任务的解被P2找到，但这条轨迹十分危险，在18.18 s处离地面较近且仍然有较大的水平速度，考虑存在离散误差和环境扰动的情况下可能会导致任务失败，两任务参数如下。

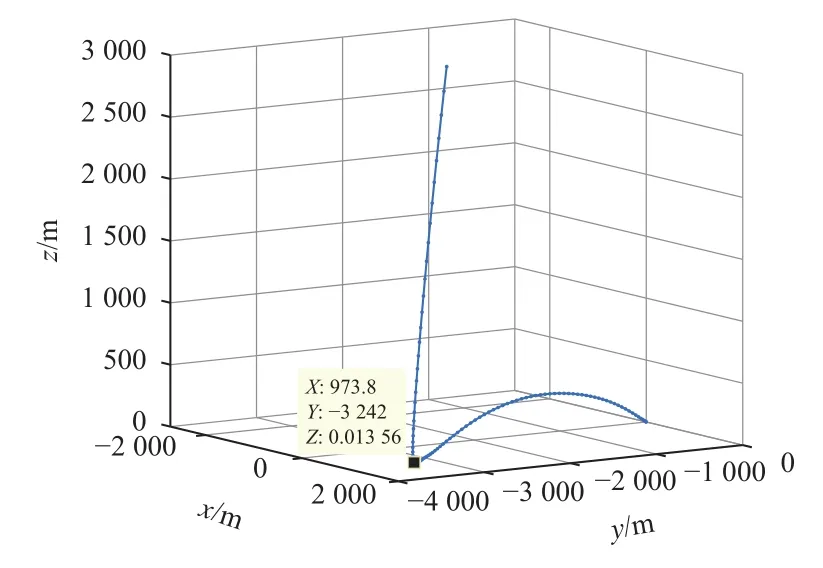
图25 P2解得任务181的规划轨迹Fig.25 The optimal trajectory of case 181 by using P2 convexification method

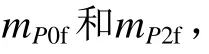
图26 P2解得任务181的速度轨线Fig.26 Velocity profiles of case 181 by using convexification method P2

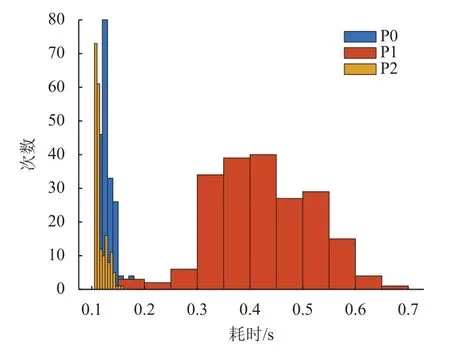
图27 200组随机任务打靶耗时统计图Fig.27 Computing time statistics of 200 random cases

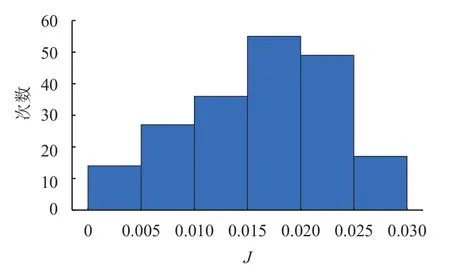
图28 200组随机任务中指标J的统计图Fig.28 The index J statistics of 200 random cases

以上求解过程都未引入信赖域约束，若增加状态量信赖域约束，在表1仿真参数下采用P0进行求解，每种信赖域各计算100次，图29显示对解最优性并未有明显改善。图30为不同信赖域下求解耗时统计。前3条轨线和无信赖域约束求解结果基本重合，第4条轨迹消耗燃料相比前3条节省了0.032 7 kg，仅占总质量的0.065 4%，但耗时相对较长。在本问题中基本可视信赖域为冗余约束。

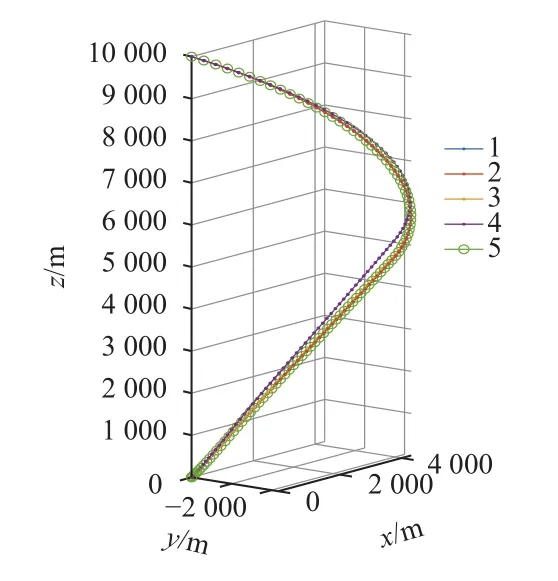
图29 不同信赖域约束下优化得到的轨线Fig.29 Optimal trajectories under different trust regions

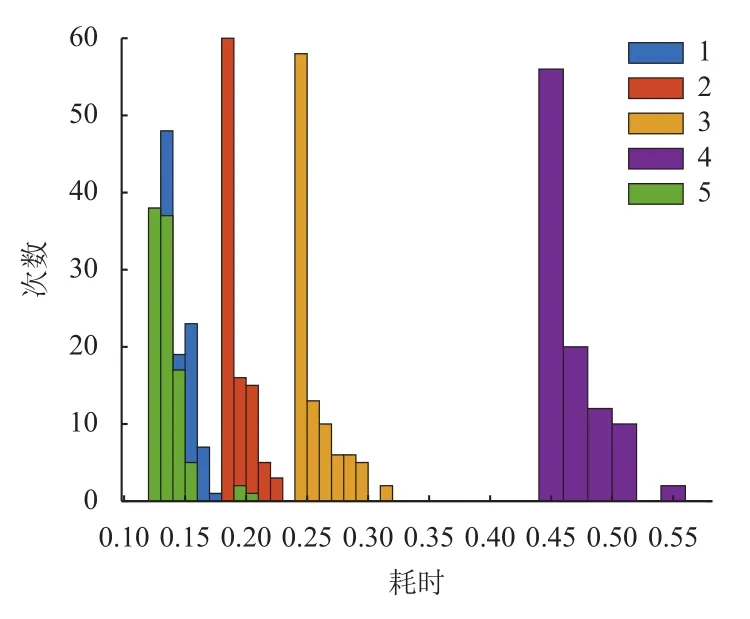
图30 不同信赖域下求解耗时统计Fig.30 Computing time statistics under different trust regions

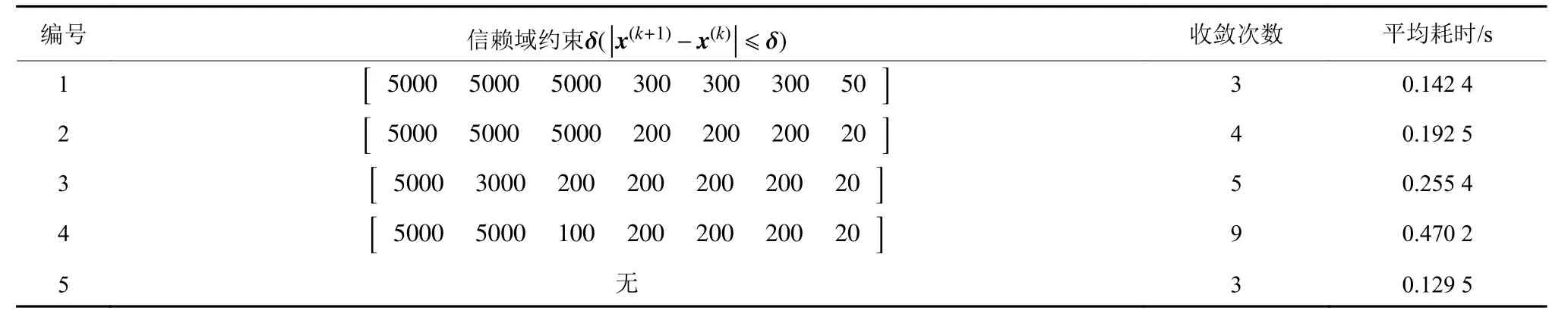
表6 不同信赖域下的求解结果Table 6 Results under different trust regions.

4 结 论

本文使用中心差分逐次线性化动力学，提高了序列凸优化算法的规范性和工程性，避免因使用推力方向余弦无损凸化和质量方程取对数凸化而引入额外的优化变量，降低了公式推导工作量和编程复杂性。通过对比证明，相对于传统动力学凸化技巧，直接线性化的求解结果并未对算法收敛性、解的最优性和终端误差造成显著影响。同时，采用性能指标相对偏差作为迭代收敛条件，使收敛条件和具体模型解耦，具有更好的普适性。

针对动力下降段最优控制问题，给出最优轨迹簇剩余燃料和终端时间的拟合函数，可解析求出近似最优终端时间，能够有效提高在线轨迹方法的效率。

本文使用的动力学模型较为简单，未考虑更多的过程约束和环境条件，如发动机推力方向约束、落地倾角约束和气动力作用，但可为复杂约束下的轨迹规划算法提供参考初始轨迹，也可为轨迹跟踪控制算法提供标称轨迹。

由于存在线性化误差和离散误差二者的复合作用，主要采用大批次数值仿真计算来评估算法收敛能力，对序列凸优化算法收敛性的严格数学证明尚比较困难，需要进一步进行深入研究。