小行星复杂形貌自适应附着轨迹动态规划方法

葛丹桐，朱圣英

（1.北京理工大学 深空探测技术研究所，北京 100081；2.深空自主导航与控制工信部重点实验室，北京 100081；3.飞行器动力学与控制教育部重点实验室，北京 100081）

引 言

小行星具有极高的科学探索价值，通过研究与探索小行星，人类可进一步开发与利用太空资源，发展并验证小行星防御技术。近两年，日本“隼鸟2号”（Hayabusa 2）与美国“奥西里斯–雷克斯”（Origins Spectral Interpretation Resource Identification Security Regolith Explorer，OSIRIS-REx）任务分别对一颗C类小行星与一颗B类小行星开展了采样返回探测[1-2]。其中Hayabusa 2已完成对小行星“龙宫”（Ryugu）的采样任务，并于2020年底将样品送回地球；OSIRIS-REx于2020年10月在小行星“贝努”（ Bennu）表面实现首次附着采样，目前正在返回地球途中。

在小行星探测任务中，目标形貌复杂多样，表面碎石、陡坡、凸包、陨石坑等障碍对探测器附着安全带来挑战[3-5]。同时，受动力学建模误差、星上导航控制误差以及太阳辐射、第三天体引力等环境扰动影响，探测器状态存在不确定性[6-7]。在日本的“隼鸟号”（Hayabusa）任务中，当探测器第一次尝试在目标小行星表面附着时，在其附近检测到未知障碍并发出紧急上升指令，而由于存在较大姿态测量误差，该指令并未执行，导致探测器在目标表面发生了多次弹跳[8]，对任务安全构成了威胁。因此，为了实现探测器在复杂形貌环境中的安全附着，有必要针对附着环境与探测器状态不确定下的轨迹规划方法展开研究，通过动态评估碰撞威胁并实时调整下降轨迹，提高小行星附着任务安全性。

现有研究中，常将轨迹规划问题转化为最优控制问题求解[9-10]。然而受星上计算能力制约，最优轨迹一般需提前在地面计算与存储，并在实际下降过程中采用比例积分微分（Proportional Integral Derivative，PID）控制、滑模控制、自适应控制等方法[11-12]对标称轨迹进行跟踪，驱动探测器到达目标着陆点附近。此类方法缺乏一定灵活性，难以根据环境实时检测结果对下降轨迹进行调整，且一旦实际动力学建模误差与环境干扰超出预期，系统状态有违背约束的风险[13]，从而可能导致任务失败。

针对动态环境中的路径规划问题，文献[14]在经典A*算法基础上提出D*算法，即动态A*算法。在已有路径点序列上，结合环境地图变化更新局部代价函数，并对局部路径点进行重规划，避免重新规划整条路径占用过多星上资源，提高规划效率。随后，进一步发展出LPA*、D* Lite、D*PO等算法[15-16]，其中D*PO算法引入多目标优化理论，通过求解帕累托最优路径点，可实现多优化目标下的路径动态规划。然而，与地面机器人路径规划相比，小行星附着任务中探测器运动受动力学、推力幅值、下降速度、末端状态等约束[17-19]，且在环境扰动与状态不确定性的共同影响下，探测器实际下降过程难以严格按照预设轨迹运动[20]。为了避免跟踪过程中探测器违背工程约束，需要在规划轨迹时考虑状态与环境的不确定性影响，设计可安全跟踪的路径点序列。

基于以上问题，本文针对小行星复杂形貌附着轨迹动态规划方法展开研究，旨在构建小行星附着多目标最优路径点序列，基于标称轨迹与实时检测环境障碍的冲突预判，形成形貌自适应的附着轨迹动态规划方法，提高探测器在小行星复杂形貌环境附着的安全性。

1 小行星附着轨迹规划模型

在小行星质心固连系下建立探测器动力学方程

其中：r为探测器位置；v为探测器速度；ω为小行星自旋角速度；g(r)为探测器在r处所受的引力加速度，其值由多面体引力场模型给出[21]；u为控制量；ap为探测器所受的太阳光压、第三体引力等环境扰动。

基于状态反馈，以上方程可在当前状态附近线性化为

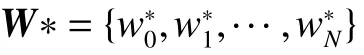
2 附着路径点动态规划

2.1 算法概述

本文所提出的形貌自适应附着轨迹动态规划方法由3部分构成——初始最优路径点规划、碰撞威胁评估与局部路径点重规划，算法结构如图1所示。

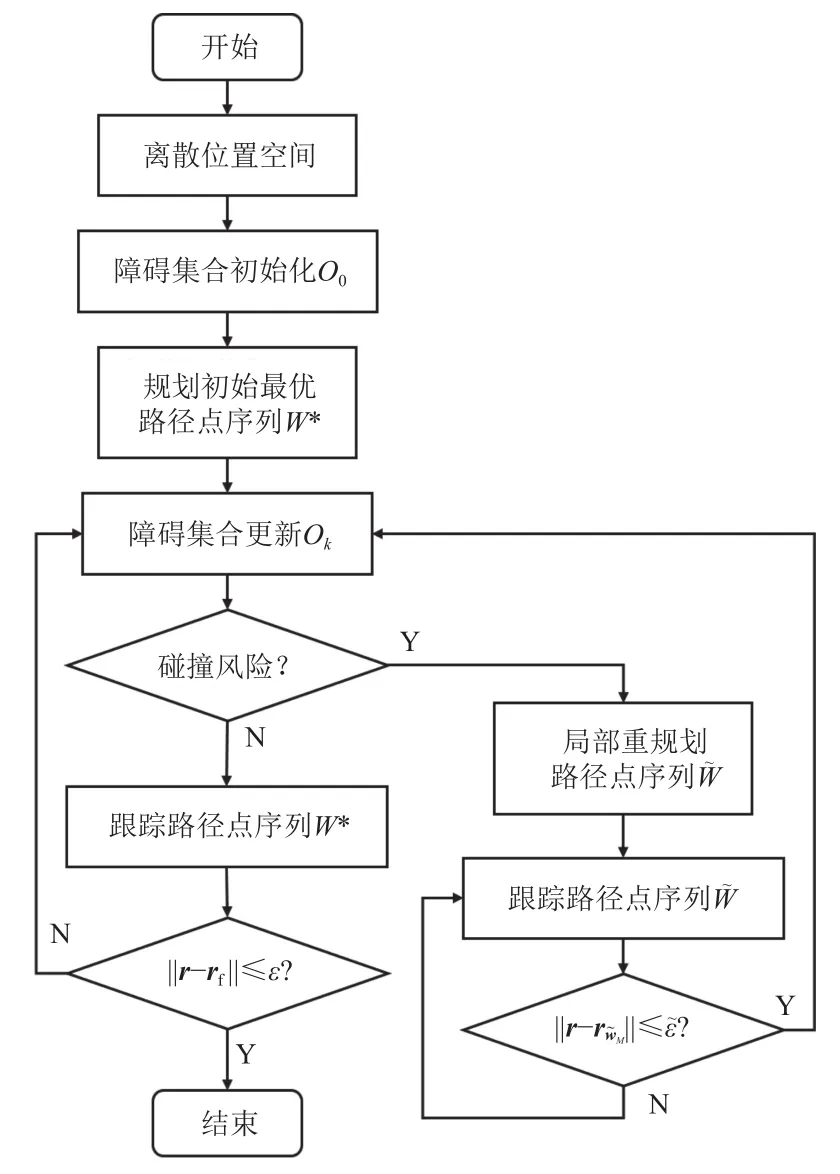
图1 算法结构Fig.1 Structure of the algorithm

算法包含以下步骤：

1）将位置空间离散成网格。结合实时导航获取的探测器状态估计结果，计算位置误差椭球为[22]

其中：µr为位置估计均值；Dr为位置估计协方差矩阵；Cr为特征根构成的对角矩阵；UE为着陆点固连坐标系到误差椭球坐标系的转换矩阵。记位置误差椭球半长轴长度为aE，则网格边长应满足l≥aE。

2）附着过程初始时刻t0，基于初始时刻环境地图障碍集合O0，规划探测器从初始位置rO到着陆点rf的帕累托最优路径点序列W∗。

3）附着过程中更新障碍集合Ok，基于探测器当前状态x(k)、初始最优路径点序列W∗，评估是否存在碰撞威胁。若无碰撞威胁，继续步骤4）；若存在碰撞威胁，跳到步骤6）。

4）结合探测器当前状态x(k)，跟踪初始最优路径点序列W∗的下一路径点。

2.2 初始最优路径点规划

小行星附着过程初始时刻，假设所有未知区域为无障碍空间，将与障碍重合的网格标记为禁飞区，剩余网格视为安全区，网格的中心点集合构成路径点解空间。在搜索路径点时，从初始位置rO开始，依次考虑当前节点相邻3n−1节点，其中n为维数，将位于安全区的节点放入OPEN表中。结合小行星附着任务能耗、着陆精度、障碍规避3个方面的任务需求，设计以下目标函数。

代价目标函数c1(wi)用于估计探测器从初始位置w0转移到节点wi的代价，其值等于从初始位置w0到达上一节点wi−1的转移代价与从节点wi−1到达节点wi的转移代价之和

在初始位置时c1(w0)=0。从安全节点wi−1到达安全节点wi的转移代价∆c1(wi−1,wi)由两节点之间距离矢量的模‖d(wi−1,wi)‖与探测器运动方向共同决定

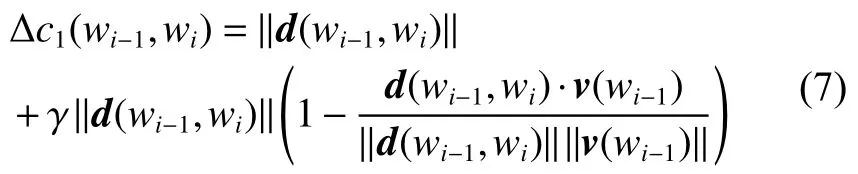
对于禁飞区节点，进入或从禁飞区网格出来的转移代价记为+∞。着陆点目标函数c2(wi)作为启发式函数，通过计算节点与着陆点间的直线距离

确定不同节点在搜索过程中的优先级，提高路径规划效率。风险评估目标函数c3(wi)用于评估探测器转移至节点wi的过程中，在状态不确定性影响下与最近障碍发生碰撞的概率。受下降过程中动力学建模误差、导航误差、执行误差等因素影响，探测器的实际运动轨迹可能偏离路径点连线，使得路径规划阶段满足要求的轨迹在附着跟踪过程中超出任务约束。假设轨迹跟踪最大偏移量为δ，定义风险评估目标函数c3(wi)为

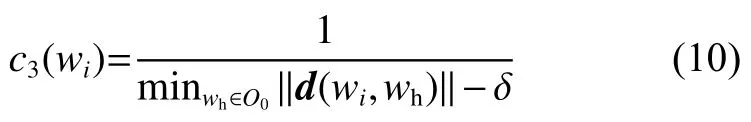
其中：wh为障碍集合O0中的节点。

节点wi距离wh越近，探测器与障碍碰撞概率越高，风险评估目标函数c3(wi)取值越大。通过在风险评估目标函数中引入冗余量δ，可在搜索路径点时避免选取禁飞区相邻节点，使得探测器即使在最大跟踪误差下，仍能与障碍保持安全距离。

2.3 碰撞威胁评估

附着过程中，探测器通过星上敏感器如相机、激光雷达等对测量范围内的碎石、陡坡、凸包、陨石坑等障碍进行检测[13]。为了提高附着安全性，除了考虑探测器在状态不确定条件下的障碍碰撞概率，还需对星上新检测到的环境障碍与初始最优路径点序列W∗间是否存在冲突进行实时评估。

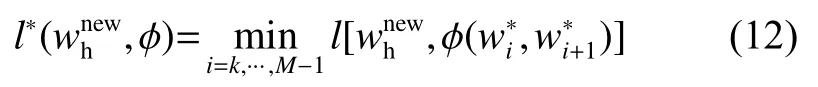
2.4 局部路径点重规划

3 路径点鲁棒跟踪

第2节给出标称情况下探测器附着的多目标最优路径点序列，并在环境与轨迹存在冲突时，局部调整路径点实现障碍规避。而在实际附着过程中，探测器还需要对规划得到的路径点序列进行实时跟踪，生成满足系统动力学的安全附着轨迹。

在现有跟踪控制方法中，模型预测控制[23-24]根据系统最新状态，通过在有限时域上反复求解最优控制问题，在降低优化问题求解难度的同时，提高了多约束下系统跟踪性能。本节基于模型预测控制方法构造路径点跟踪控制律，通过考虑动力学方程环境扰动与模型线性化导致的有界建模误差，实现对所规划路径点序列的实时鲁棒跟踪。

具体来说，在探测器跟踪路径点序列向着陆点运动过程中，结合探测器动力学方程与实时状态更新，采用模型预测控制方法构造路径点跟踪优化性能指标，通过对探测器控制量进行优化，生成动力学建模误差下的路径点序列跟踪轨迹。

其中：Nf为有限时域长度；k为当前有限时域的第k步；Q,R为地面提前选定的正定矩阵，为保证优化结果收敛性，矩阵 P通过求解里卡蒂方程得到

4 数值仿真

图2 仿真地形与初始最优路径点序列Fig.2 Simulated terrain model and the initial optimal waypoint sequence

图3 X-Z平面内的初始最优路径点序列Fig.3 The Pareto optimal waypoint sequence on the X-Z plane

图4 实际跟踪轨迹在X-Z平面投影Fig.4 The projection of the landing trajectory on the X-Z plane

图5 探测器位置与速度在X轴和Z轴的变化Fig.5 Positions and velocities of the spacecraft on X and Z axes

图6 X-Z平面内的重规划路径点序列Fig.6 The re-planning waypoint sequence on the X-Z plane

5 结 论

本文结合小行星探测器状态不确定性与实时障碍检测结果，对复杂形貌小行星附着轨迹动态规划方法展开研究。在多目标优化理论基础上，考虑附着过程工程约束，通过鲁棒跟踪最优路径点序列并局部重规划冲突路径点，得到对小行星复杂形貌环境具有自适应能力的轨迹动态规划方法。仿真结果表明该算法可生成与环境相匹配的安全附着轨迹，并在新障碍出现时，通过调整最少路径点对障碍进行有效规避。