优化的基于错误学习问题的CKKS方案

郑尚文，刘 尧，周潭平，2*，杨晓元，3

（1.武警工程大学密码工程学院，西安 710086；2.中国科学院软件研究所，北京 100090；3.网络和信息安全武警部队重点实验室（武警工程大学），西安 710086）

（∗通信作者电子邮箱850301775@qq.com）

0 引言

全同态加密（Fully Homomorphic Encryption，FHE）允许在不解密的状态下对密文进行任意运算，且解密后结果与其对应明文进行同样运算的结果相等。这一优良特性与云计算条件下对数据隐私保护的需求十分契合，具有广阔的应用前景。2009 年Gentry［1］首先构造了第一个基于理想格的全同态加密方案Gen09，并且描绘了实现纯全同态加密的“蓝图”——同态运行解密电路。之后，一系列（全）同态加密方案［2-7］相继被提出，同态加密成为信息安全研究领域的热点，得到迅速发展。目前，同态加密在基因组分析［8］、医疗［9］、金融［10］和安全多方计算（Secure Multi-Party Computation，MPC）等领域［11-12］发挥了重要作用。

CKKS17（Cheon-Kim-Kim-Song 2017）同态加密方案由Cheon 等［7］在ASIACRYPT17（2017 International Conference on the Theory and Application of Cryptology and Information Security）会议上提出，支持对浮点数进行近似计算，效率较高，是目前最重要、最具前景的同态加密算法之一。与以往同态加密方案明文空间和噪声空间分隔开的设计不同，CKKS17的明文空间没有取模过程，因此也不能在解密后通过相应的模运算来得到准确的解密结果:它将噪声视为明文的一部分，而噪声一方面来源于加密方案中为保证安全性而引入的错误，另一方面也来源于近似计算中的舍入误差，密文解密后不能将明文中的噪声去除，只能以预定的精度输出明文的近似值。在同态运算过程中，计算结果的高有效位（Most Significant Bits，MSBs）能够保留，而不精确的低位比特（Least Significant Bits，LSBs）则在RS（ReScaling）过程中被舍去，以此管理结果密文对应的明文尺寸，这也使得方案所需最大密文模数随乘法深度由指数增长降为线性增长。CKKS17 方案提出之后，研究人员在此基础上做了进一步的研究。2018年，Cheon等［13］提出了CKKS17的Bootstrapping技术，将其由层级同态加密推广至完全同态加密，并提出了支持余数系统（Residue Number System，RNS）分解的CKKS17 方案的变体［14］；后续，Chen 等［15］对Bootstrapping 过程进行了优化，使自举的时间降低两个数量级；2019年，Chen等［16］提出了CKKS17的多密钥版本CDKS19（Chen-Dai-Kim-Song 2019），并对该方案应用于神经网络模型的效率进行了测试。

虽然同态加密为云计算中的数据隐私保护提供了一个良好的解决方案，但由于同态加密方案需要对庞大的密态数据进行同态运算，因此在存储和传输加密数据时，无疑会给用户造成较大的通信开销负担。同时，错误学习（Learning With Errors，LWE）型CKKS 方案的重线性化过程［17］所需的计算密钥规模庞大，计算复杂，也影响了方案的实际运用。低位比特丢弃（low-order Bits Discarding algorithm，BD）的思想最早出现于格密码中，Zhou 等［18］将其应用于同态加密以提高效率。在此基础上，本文结合LWE型CKKS方案的密文结构，通过舍去密文中的部分低位比特来减少存储的比特数，从而降低了重线性化过程中计算密钥的大小和计算开销，提高了方案的存储和计算效率。

1 相关知识和关键技术

1.1 相关定义

定义1误差学习问题［19］。

设λ为安全参数，令n=n(λ)是一个整数维数，q=q(λ) ≥2 为一个整数，χ=χ(λ)是整数上的一个分布。判定型LWEn，q，χ定义为区分下面两个分布:1）第一个分布，均匀地从中选取产生(ai，bi)；第二个分布，均匀选取s←和计算bi=〈ai，s〉+ei，组成

定义2B⁃bound分布［17］。

对于一个整数分布集合{χn}n∈N，如果下列等式成立

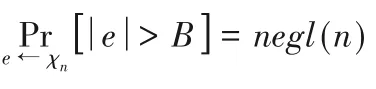
则称整数分布集合{χn}n∈N是B⁃bound分布。

1.2 关键技术

方案运用了BitDecomp(∗)、Powersof2(∗)［4］及张量积等方法，具体操作为:

1）BitDecomp(x∈，q):对于输入向量x∈，BitDecomp将其表示为x=其 输出为，其中uj∈R。显然，x=

2）Powersof2(x∈，q):对于某 个输入向量，Powersof2 是BitDecomp的逆过程，其输出为(x，2·x，…，∈。由上述定义，对于给定两个维数相同的向量a、b，不难验证下面等式:

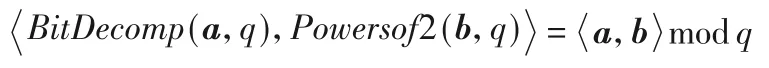
3）设u、v分别为n、m维向量，则向量u、v的张量积定义为u⊗v=(u1v1，u1v2，…，u1vm，…，unv1，…，unvm)。根据张量积和内积的定义，可以证明如下等式:

2 低位方法的应用

2.1 CKKS17方案

CKKS17 方案［7］主要包括六个基本算法（KeyGen，Enc，Dec，Add，Mult，RS），本文主要对基于LWE 的CKKS 加密方案进行优化，下面对该方案作以简要介绍。首先，该方案利用Ecd、Dcd及缩放因子Δ来实现消息与明文的相互映射。以消息为复数，明文以分圆多项式环上的元素为例，Dcd首先将明文多项式m(X)除上因子Δ，然后计算该明文多项式在分圆多项式ΦM(X)根处的函数值，并取整，得到最终的复数消息向量。而Ecd即为Dcd的逆变换，具体过程为:

其中:映射π-1表示将复数映射到本身与其共轭复数的集合；σ-1则利用离散傅里叶变换来实现复数向量向分圆多项式环上元素的变换。

在密钥初始化阶段，基于LWE 问题生成公私钥对(pk，sk)以及计算密钥evk，用于对明文加解密以及乘法中的重线性化。与其他基于LWE 加密方案不同的是，CKKS17 方案中引入了一个新的概念:rescaling，它应用在乘法密文重线性化步骤后，通过将被加密的明文除上一个整数，并利用浮点数和科学计数法在近似计算中的“四舍五入”来去除明文中一些不精确的低位比特，从而使得在同态计算期间，编码前后的消息的大小保持基本不变，同时也保证了方案所需的最大密文模数随运算电路深度呈线性增长，极大提高了方案的效率，促进了方案的实用化发展。根据基于RLWE（Ring LWE）的CKKS 方案编写了开源的同态加密库HEEAN。

2.2 低位比特丢弃方法的构造

在同态加密方案［20］的实际使用中，为了提高方案效率，一般使用中国剩余定理（Chinese Remainder Theorem，CRT）将大密文分割成小块密文（模数较小的密文）进行操作，但进行重线性化步骤时仍需要将其转化为一般的表示形式。重线性化过程所使用的计算密钥的尺寸很大，这是影响方案效率的重要因素。针对这一过程，本文提出了一种低位比特丢弃方法，通过有选择地舍弃密文中的部分低位比特从而相应地减小重线性化密钥的尺寸来提高方案效率。下面对本文方法的主要思想进行介绍。

计算机中数的存储通常采用二进制存储，不同比特所处的位置不同所代表的权重也不相同，因此，可以通过舍弃存储密文每一个分量的部分低位比特来减少存储空间，密文整体比特数的降低也能够提升密文通信的效率。由于密钥采样的分布通常是一些“小分布”（采样值的绝对值相对较小），因此丢弃低位比特对噪声的贡献并不会很大。同时在方案的重线性化过程中，丢弃低位比特能够减小计算密钥的大小，从而降低由于重线性化加密私钥所产生的噪声，其具体构造如下。

定义3低位比特丢弃（BD）方法。

设密文c∈，δ为丢弃的低位比特位数，比特丢弃方法的主要做法是丢弃输入密文c中n个分量各自的低位δ比特，得到cBD=BD(c，δ)∈，其中cBD中每一个分量根据丢弃比特向量cδ最高位0、1取值的不同，有选择地加上进位。即当cδ的首位比特为1 时，向前进位；当cδ的首位比特为0 时，不进位，具体如图1所示。

图1 低位比特丢弃方法Fig.1 Low-order bits discarding method

选择性地加上进位能够使得丢弃低位比特后的密文向量与原始密文向量的差值更小，更好地控制噪声的增长。单纯的比特丢弃技术并不会降低密文的噪声，但是在密文进行同态运算时丢弃低位比特能够减少相应噪声并提高计算效率，具体到方案同态运算中的应用如下。

2.2.1 低位比特丢弃在同态加法中的应用

同态加法操作由于不涉及进行复杂昂贵的重线性化操作，只需要对输入的两个密文丢弃相应的低位比特即可，如下所述:

设c1，c2∈是两个加法密文输入，首先对两个密文进行低位比特丢弃，得到=BD(c2，δ)。输出同态加法的结果密文cadd=

2.2.2 低位比特丢弃在同态乘法中的应用

3 基于低位比特丢弃的LWE型CKKS方案

3.1 方案构造

选取合适的基p＞0，模数q0，令ql=pl·q0，0 ＜l≤L。HWT(h)［21］为有符号的、汉明重量为h的N维{-1，0，1}N向量集合，λ为安全参数。在计算密钥的生成和同态运算中运用了低位比特丢弃方法进行优化，基于低位比特丢弃的LWE 型CKKS方案主要包括以下六个算法:

1）密钥生成算法KeyGen(1λ)。

①选取质数p和整数q0、τ，设ql=plq0，l=1，2，…，L，合理选取参数N=N(λ，qL)和B⁃bound 错误分布χ=χ(λ，qL)作为LWEN，qL，χ问题的参数。输出params=(n，qL，χ，τ)。②随机选取s=HWT(h)，私钥sk←(1，s)∈。随机均匀选取A←，e←χτ。令b=-As+e(modqL)，输出方案的公钥pk=(b，A)∈

2）加密算法Enc(m，pk)。

对于一个整数m∈Z 的明文，随机均匀选取一个向量r←{0，1}τ。输出其密文c←(m，0)+pkT·r∈

3）解密算法:Dec(c，sk)。

对于一个密文向量c与私钥sk，解密算法为m'=

4）同态加法ADD(c1，c2)。

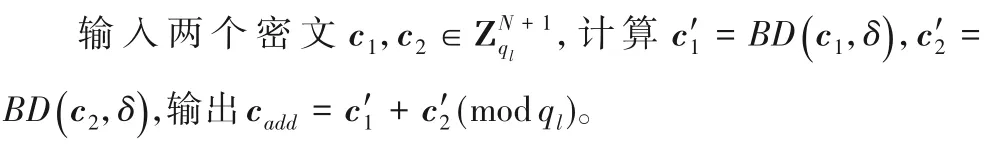
5）同态乘法Mult(c1，c2)。

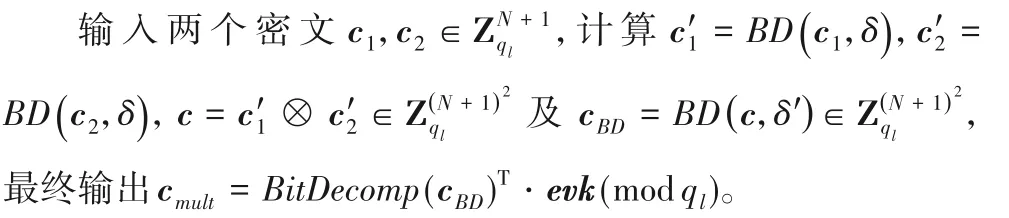
6）重缩放RSl→l'(c)。

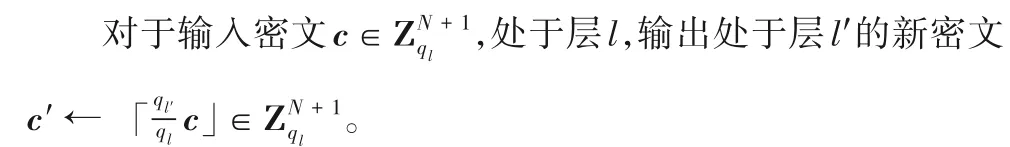
3.2 正确性

本文方案的加解密正确性与原始的CKKS17 方案大致相同，在此不作阐述，主要论述在运用低位比特丢弃方法之后同态加法和同态乘法的正确性。设c1，c2分别是对m1，m2∈Z加密的密文，噪声分别为e1，e2。

3.2.1 加法正确性

其同态加法输出cadd=c1+c2，满足如下等式:

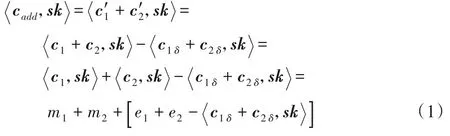
令c1δ和c2δ分别代表相应密文向量丢弃低位δ比特后的差值，当

Δ为消息与明文之间转化的缩放量，方案正确性成立。

3.2.2 乘法正确性

其同态乘法输出cmult=c1×c2，满足如下等式:

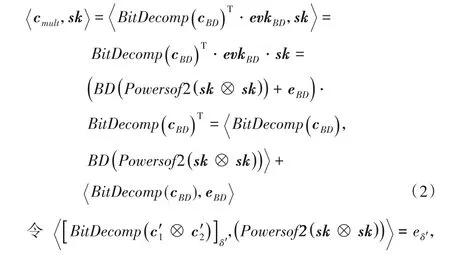
故:

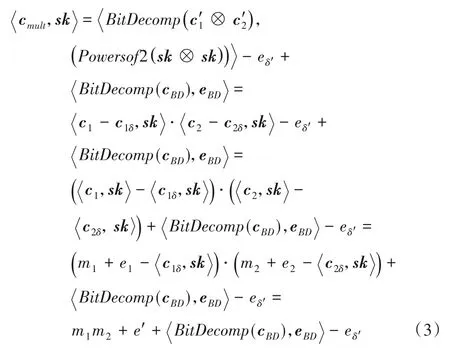
其中，[BitDecomp、ciδ(i=1，2）分别代表cBD、ci丢弃δ′位比特向量后与原来向量的差值，即:

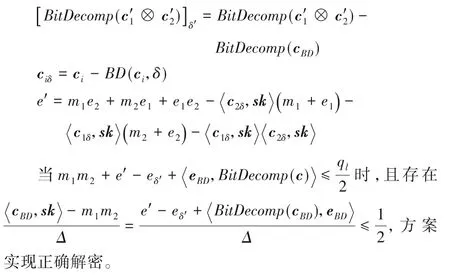
4 方案分析

4.1 噪声分析

假设方案加密的明文上限为ν，密文维数为N+1，δ、δ′为相应向量丢弃的比特位数。根据ei=rTei(i=1，2)，ei←χ，s=HWT(h)，sk←(1，s)∈，下面对同态加法和同态乘法的噪声上界进行分析。

4.1.1 同态加法噪声

由式（1）可得加法噪声:

4.1.2 同态乘法噪声

综合式（2）、（3），有:

与原来的同态乘法噪声相比，在δ与δ′取合适值时，本文方案既能降低同态乘法运算时计算密钥的复杂性，也能降低噪声和密文的存储开销。

4.2 效率

本文所提出的低位比特丢弃方法能够减小重线性化密钥的尺寸，使原来的计算密钥维度从降低 至；定义计算复杂性等于向量中各数值元素参与运算的次数，本文方案通过丢弃低位比特，同态乘法的计算复杂性得到明显减小，降低了计算开销；同时，该方案进行通信的每一个密文向量均减少了δ比特，提高了通信效率，也减小了密文向量的存储开销，使该方案在实际使用过程中更加快速高效。本文方案与LWE 型CKKS 方案的性能对比如表1 所示。由表1 可以看出，相较LWE 型CKKS 方案，本文所提优化方案使得计算密钥的维度减少，使得同态乘法的计算复杂性降低。

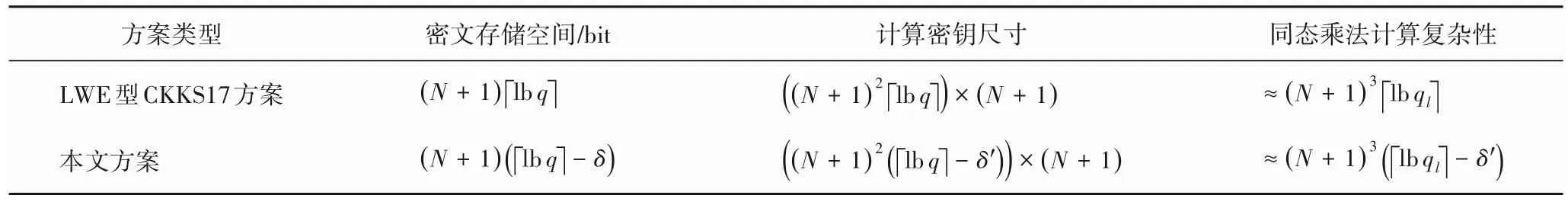
表1 本文方案与LWE型CKKS方案的性能对比Tab.1 Performance comparison between proposed scheme and LWE type CKKS scheme

4.3 安全性

本文提出的低位比特丢弃方法在CKKS17 方案上进行了优化，其密钥生成算法、重线性化技术及加解密过程仍与CKKS17保持一致，安全性依赖于LWE 问题的困难性。同时，低位比特丢弃技术可视为密文向量的低位比特与另一向量的“与”过程，对安全性没有影响。因此，本文提出的低位比特丢弃方法设计的优化加密方案的安全性与CKKS17 方案的安全性相同，可以达到语义安全。

5 结语

CKKS17方案作为目前实际应用中重要的一个方案，具有支持浮点数运算的优点。本文在原有方案的基础上通过舍弃密文低位比特的方法，对其进行了优化，提出了优化的LWE型CKKS 方案。相较于现在的方案，本文所优化的方案缩减了重线性化密钥的尺寸，使得同态计算的效率得到了提升，且密文向量比特的减少也使得该方案在实际运用过程中的存储和通信效率得以提高。基于RLWE 的CKKS 方案能够将多个密文打包进行计算，效率更高，下一步将针对RLWE 型CKKS方案的优化进行研究。