基于聚类和实例硬度的入侵检测过采样方法

王 垚，孙国梓

（南京邮电大学计算机学院，南京 210023）

（∗通信作者电子邮箱sun@njupt.edu.cn）

0 引言

网络安全已经成为计算机系统以及计算机网络中的热点问题，引起越来越多的关注。一些常见的网络攻击类型，诸如分布式拒绝服务（Distributed Denial of Service，DDoS）攻击、僵尸网络（Botnet）等，一旦攻击得手将造成严重后果，例如2019年10月22日，亚马逊公司服务器遭DDoS攻击，攻击者试图通过垃圾网络流量堵塞系统，导致服务无法访问，攻击持续整整15个小时，造成的损失难以估量。

作为保证网络安全的重要技术之一，入侵检测系统（Intrusion Detection System，IDS）是网络安全防护方案的重要组成之一［1］。入侵检测系统是从计算机和网络中收集与分析流量信息，判断网络中是否出现一些异常行为。现代入侵检测系统呈现机器学习、深度学习等技术的高度融合的趋势，有效提高了网络攻击的检测效率。

基于机器学习的入侵检测模型已取得较好的性能，但数据不平衡仍是影响大多数入侵检测模型性能提升的瓶颈［2］。类不平衡会导致训练模型过拟合，在机器学习领域中，为解决不平衡问题，常采用合成少数类过采样技术（Synthetic Minority Oversampling TEchnique，SMOTE）［3］等采样方法平衡数据。但在入侵检测中，数据集往往更复杂、规模更大，不平衡程度更严重。传统的采样方法进行采样后会导致数据重叠，降低检测率。一些研究人员指出，不平衡问题是数据科学面临的十大挑战之一［4］，同时数据不平衡问题也是机器学习中的研究热点之一。在入侵检测数据中往往攻击类型数据相对较少，正常流量的数量则相对偏多，但攻击类型数据往往包含关键检测信息，而在不平衡的入侵检测数据上训练机器学习模型，会导致模型偏向于拟合正常流量数据，泛化能力弱。

为了解决入侵检测中的不平衡问题，在改进传统过采样算法缺点的基础上，本文提出了基于聚类和实例硬度的入侵检测过采样方法（Clustering and instance Hardness-based Oversampling method for intrusion detection，CHO）。首先，计算实例硬度（Instance Hardness，IH）［5］，准确识别难以正确分类的样本，再通过聚类算法结合实例硬度识别“安全”区域，并依据统计学最优分配原理进行过采样。

本文的主要工作如下:

1）提出了一种新的过采样方法，解决了入侵检测中常见的数据不平衡问题。不同于SMOTE 等传统方法，所提方法通过聚类识别数据分布，然后在同时考虑数据的疏密程度和类重叠的情况下生成数据，在测试数据集上有效提高了分类器的分类性能。

2）通过实例硬度，对网络流量数据进行分析。

1 相关工作

1.1 入侵检测系统

入侵检测系统（IDS）分析来自网络内部和外部的网络流量，能够有效地检测出异常流量。IDS 与机器学习、深度学习技术结合，能够有效增强网络系统的安全性。机器学习算法被广泛运用到IDS 之中，文献［6］将改进的决策树（Decision Tree，DT）算法用于入侵检测系统。文献［7］利用随机森林（Random Forest，RF）进行入侵检测。深度学习技术在IDS 中也被大量运用，比如文献［8］将改进的多层感知机（Multi-Layer Perceptron，MLP）用于DDoS 攻击的检测。然而，以上研究很少关注到入侵检测中的数据不平衡问题。

1.2 不平衡学习

机器学习中的不均衡问题，主要表现为数据集各类样本数值上存在差异。为表示数据的不平衡程度，引入不平衡率（Imbalance Ratio，IR）。以二分类情况为例，不平衡率可表示为:

其中:Nmaj代表数据中多数类数据的数量；Nmin代表少数类数据的数量。关于平衡的阈值一般认为是1.5［9］，即数据不平衡率大于1.5，那么认为该数据是不平衡的。加拿大网络安全研究所（Canadian Institute for Cybersecurity，CIC）2017 年公开的CICIDS2017 数据［10］，较全面地反映了现代网络攻击的类型。该数据由多组关于不同攻击类型的子数据集构成，总体上正常流量和异常流量的不平衡比达到4.081 4∶1，其中各子数据集也是普遍不平衡的，比如CICIDS2017 中关于渗透（Infiltration）攻击的流量数据只有36个样本，子数据不平衡率超过8 000。数据的不平衡导致入侵检测模型无法从有限的样本中充分获取攻击流量的信息。

重采样技术被用于解决不平衡问题，可分为过采样、欠采样以及混合采样三类。随机欠采样（Random Under-Sampling，RUS）是最易于实现的欠采样方法，从多数类中随机选择样本，然而这可能导致丢失重要信息。过采样方法则扩充少数类数量以达到平衡数据的目的。混合采样则将两者结合。SMOTE 是一种经典的过采样技术，被广泛应用于入侵检测中［11-12］:首先，为每个少数类样本搜索K个近邻样本；然后，从这些最近邻中随机选择一个邻居样本，在每个少数类样本与其所选样本之间的连线上合成一个新数据，称为插值法。SMOTE 启发了很多后续研究工作，如基于边界的SMOTE（Borderline SMOTE）算法［13］、自适应合成过采样（ADAptive SYNthetic sampling，ADASYN）［14］等过采样方法相继被提出。此外，深度学习技术也被用于处理不平衡问题，文献［2］运用生成对抗网络（Generative Adversarial Network，GAN）生成少数类数据，用于入侵检测模型训练；文献［15］运用人工神经网络（Artificial Neural Network，ANN）拟合少数类数据，并对多数类数据进行预测，选取预测误差较大的数据进行训练。

1.3 硬度

实例硬度表示样本X被数据集中其他样本构造的分类器错误分类的概率［5］。硬度的取值范围为0～1。硬度值越接近0，表明该样本可以被几乎所有分类器正确分类，而硬度为1的样本则表明被所有分类器误分类。硬度衡量的是样本被分类器正确识别的难度。位于重叠区域的样本通常具有更高的硬度值，而离群值的硬度可能很大也可能很小［5］。

为了解释实例硬度，将数据表示为〈X，Y〉，其中Y是样本X的所属类别，用f表示从样本X转换为类别Y的函数，即有f:X→Y，那么P(X|Y，f)表示f将Y正确分配给X的概率。实际上f是由训练在数据d上的机器学习算法g得到的，那么可表示为f=g(d，a)，其中a代表算法g的参数。为了准确、客观地衡量实例硬度，文献［5］将实例硬度定义为:

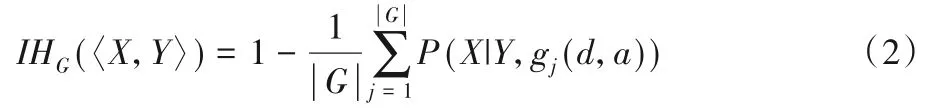
其中，G代表一组机器学习算法，且有gj∈G。基于实例硬度，文献［16］提出混合袋装（Mixed Bagging，MixBag）模型，将硬度应用到袋装集成过程中，提升了分类器性能。

1.4 最优分配

分层抽样是统计学中关于抽样的重要方法，该方法可以从总体中获取更具有代表性的样本。首先将整体数据按照某种特征分为若干层，从每一层中再按照一定规则抽取若干样本组成总样本。关于各层样本量如何分配，有多种分配方法。其中，最优分配不仅考虑到各层的大小，把各层进行抽样调查的费用也纳入考虑范围。

假设样本总数为N，抽样总数为n，共分为L层。各层大小为N1，N2，…，NL，各层抽取的样本大小为n1，n2，…，nL，各层标准差分别为S1，S2，…，SL，并假设Eh为第h层中抽取一个单元进行调查的平均费用，同时h=1，2，…，L，那么最优分配公式可表示为:

各层抽取的样本数量，由各层大小、标准差和“调查费用”决定。第h层数据的标准差越大，调查费用越低，那么该层抽取的样本数量应越多。

2 本文方法

2.1 研究目的

SMOTE 通过插值法生成数据来扩大少数类数据的范围，从而提高模型泛化能力。然而，SMOTE 忽视多数类样本的分布情况，可能导致数据重叠。为了更好地控制数据生成的范围，Borderline SMOTE 则将数据生成在特定的边界，然而对于高维入侵检测数据，确定合适的边界是十分困难的。

文献［17］提出了基于聚类的合成过采样（Cluster-based Synthetic Oversampling，CSO）方法。该方法通过对数据聚类得到不同的簇，在簇心和其近邻样本之间生成新数据，避免了离群值对采样过程的影响，但该方法存在以下缺点:将待生成的数据量平均分配给各簇，没有考虑数据分布的疏密；生成的数据多样性不足等。

文献［18］将聚类算法与SMOTE 相结合，提出了K均值SMOTE（K-means SMOTE）方 法。该方法通过K均 值（K-means）聚类学习数据分布，然后计算各簇的密度，密度越小的簇分配的数据量越多，再利用SMOTE 完成数据合成。虽然该方法考虑到数据分布的疏密性，但同样忽视了类重叠的影响。

因此，本文提出了一种新的过采样方法，在同时考虑数据分布和数据重叠的情况下对数据采样，以避免重叠，达到类间平衡的同时也实现类内平衡，以解决网络入侵检测中的不平衡问题。

2.2 方法设计

本文提出了基于聚类和实例硬度的入侵检测过采样方法（CHO），CHO 利用聚类识别数据分布，并通过实例硬度和最优分配原理指导过采样。

关于实例硬度的应用，主要工作体现在:1）对数据聚类后，将不同簇中数据的平均硬度作为一种调节簇所分配数据量的权重；2）通过硬度值确定安全的区域，然后在安全区域内生成数据，安全区域受到类重叠的影响是小于非安全区域的。

首先，将输入的数据集分解为多数类Dmaj和少数类Dmin。CHO 对Dmin进行Canopy 预聚类［19］，Canopy 使用一种简单、快捷的距离计算方法将数据集分为若干可重叠的子集；Canopy聚类无需指定簇数，可作为K均值等聚类方法的预处理，通过Canopy预判K-means++方法须指定的簇数。

将Canopy 聚类后得出的簇数作为K-means++算法的聚类总数M，并进行聚类，得到簇C1，C2，…，CM。通过聚类获取数据分布的信息，可以使得生成数据在聚类内生成，维持原有的数据分布。考虑到不同的簇具有不同的疏密程度，数据越紧密则标准差越小，标准差越大则数据越离散、分布越稀疏，那么需要分配更多的数据量来实现簇间平衡，填补不同疏密程度间的差异。

同时，不同的簇受到类重叠的影响也是不同的。为了衡量重叠程度，将硬度作为CHO 的输入。为简化硬度的计算，采用KDN（K-Disagreeing Neighbors）［5］来测算少数类对应的硬度数组V，KDN 值与数据重叠的程度正相关，是一种数据真实硬度的度量方法，计算方法如式（4）；为使KDN 值更精确，设定近邻个数K=10，并以此计算输入数组V，把计算得出的KDN 值作为硬度值，并组合为数组，将少数类数据的硬度数组作为输入；聚类后拆分数组，分别得到簇Ci对应的硬度数组Vi，并求出簇的平均硬度Hi。受统计学最优分配抽样方法的启发，将Hi作为最优分配中的“调查费用”；同时计算标准差Si，见式（5）；然后通过式（6）确定簇Ci分配的待生成样本数量占待生成数据总量的比重ωi。

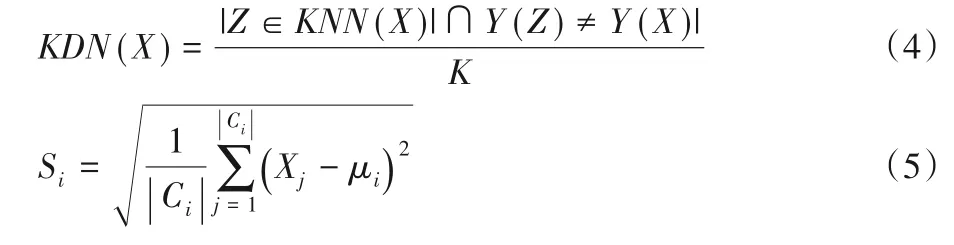
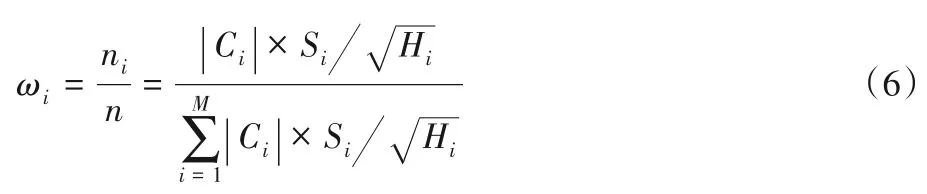
式（4）中:Y(X)表示样本X的类别；Z表示在X的K最近邻（K-Nearest Neighbor，KNN）中样本与X类别相异的样本。式（5）中:μi代表簇Ci对应的均值；Xj为Ci中的样 本。式（6）中:n表示待生成的样本总数；|Ci|为第i个聚类中样本总数；ni代表簇Ci中应生成的样本数量，反映如果簇Ci的标准差越大，硬度越低，那么应生成的数据越多，即ni在n中所占比重ωi越大。该方法不仅考虑了数据的疏密性，也考虑到了类重叠等带来的影响，通过最优分配确定在簇Ci中应生成的数据量。

最后，CHO 通过硬度值确定簇Ci中的安全区域，安全区域内的数据都具有较低硬度。在安全区域中随机选择两个样本，这里用X1和X2表示选择的第一个和第二个样本，运用插值法生成新样本Xnew:

其中q表示0～1的随机数。重复这个过程，直到Ci中新生成的样本数量达到ni。多样性对采样方法是非常重要的，通过参数P来控制最终生成数据的多样性，表示的是簇中安全区域内样本总数与簇内样本总数之比。P值越大，生成的数据多样性越高。当P=1，表示在Ci中任意两个样本之间生成数据；设定参数P的目的在于使安全区域内生成足够多样的数据。综上，CHO具体处理步骤如算法1所示。

算法1 基于聚类和实例硬度的入侵检测过采样方法。

输入 少数类数据Dmin，过采样率R，多样性参数P，少数类数据对应的硬度数组V；

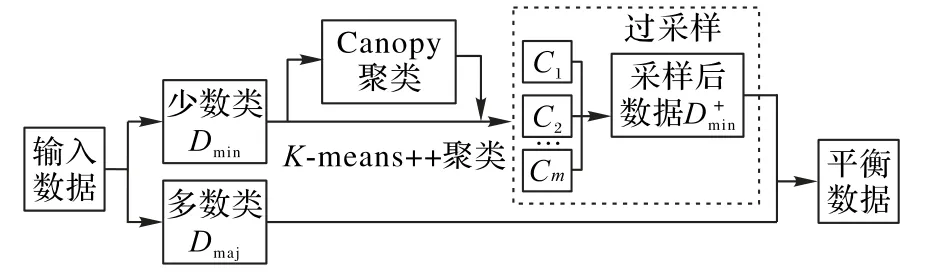
图1 综合采样流程Fig.1 Flow chart of synthetic sampling

传统SMOTE 方法在近邻样本间生成数据，可能产生噪声数据，所提方法通过聚类和实例硬度识别重叠程度小的特征空间，在该空间中合成数据，降低生成噪声的可能性；不同于CSO 方法围绕聚类中心生成数据，所提方法通过最优分配原理合理计算各簇应生成数据量，并选取簇内低硬度样本进行数据合成，减小重叠的影响；K-means SMOTE 考虑到数据分布的疏密，但计算密度的方法过于复杂，所提方法通过计算标准差衡量数据间的离散程度。综上，K-means SMOTE 等方法虽然关注到疏密性、离群值等某些方面，却忽略了类重叠对采样过程的影响，最终影响分类准确性；所提方法则基于实例硬度，从减轻类重叠影响的角度进行优化，更有效地采样。

3 实验与结果分析

3.1 数据集

网络攻击类型不断升级，因此使用一些较新的数据集训练入侵检测模型能更有效地应对攻击。选用CICIDS2017、DoHBrw2020［20］、UNSW-NB15［21］、DOS2017［22］、Botnet2014［23］等入侵检测数据进行实验。CICIDS2017 由多组关于不同攻击类型的子数据集组成，部分子数据集相对平衡，不符合实验要求，因此从CICIDS2017中选择了关于Botnet和Infiltration两种攻击的不平衡子数据集进行实验，分别用CIC_Bot、CIC_Inf 表示；将UNSW-NB15 的训练和测试数据集组合为新数据，用UNSW 表示；而Botnet2014 数据为PCAP 包格式，采用网络流量解析工具（CICFlowMeter）［24］解析成CSV 文件，将攻击流量分别标注为DOS 和Botnet，转化为二分类数据。对入侵检测数据进行了空值替换、无穷值删除、重复数据删除等处理，实验使用清洗后的数据，见表1。

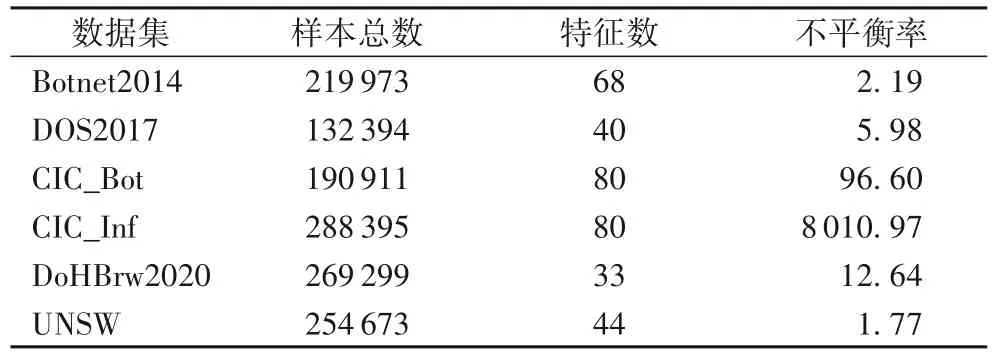
表1 实验使用的数据集Tab.1 Datasets used in experiments

3.2 评价指标

由于实验选用的数据都是不平衡的，即使随机预测也可能获得较高的准确率，所以准确率不适合作为不平衡学习任务中的评价指标。为了准确地反映模型性能，采用曲线下面积（Area Under Curve，AUC）和G-mean（Geometric mean）作为主要指标。AUC 表示受试者操作特征曲线（Receiver Operating characteristic Curve，ROC）下面积，反映模型泛化能力。G-mean表示特异度（Specificity）与召回率（Recall）的几何平均数，用于衡量数据不平衡时模型的性能。这些指标和模型性能均为正相关，指标数值越大，表明模型性能越好。

3.3 不同方法的性能对比

由于数据含有较多的冗余特征，按照随机森林得分进行特征筛选，本文研究将选择特征的个数设为20，并进行归一化处理。选择4 种过采样方法作为对比，包括SMOTE、Borderline SMOTE、ADASYN 以及K-means SMOTE，将后三种方法分别用BS、ADA 和KS 简化表示；同时实验还选用了两种欠采样方法:随机欠采样和基于KNN 的欠采样方法（NearMiss-3）［25］，分别用RUS 和NM 表示。SMOTE、BS、KS、ADA 四种方法具有共同的近邻参数，即近邻样本个数，均设为5；BS、KS 的其他参数与文献［13，18］相同；NM 的参数设定与文献［25］一致；CHO 的参数P设为0.3，并在3.4 节分析参数对所提方法性能的影响。所有过采样方法的过采样率参数均相同，使过采样后数据达到1∶1的平衡状态。以Botnet2014数据集为例，CHO、SMOTE 等过采样方法过采样率均设为1；欠采样方法的欠采样率设定类似，RUS 和NM 方法的欠采样率设为0.5。

逻辑回归（Logistic Regression）是一种广泛使用的机器学习模型，因此使用逻辑回归作为测试模型。所有采样方法均进行5 次5 折交叉验证，对每次逻辑回归的预测结果计算AUC，以平均AUC 作为指标，实验结果见表2，并统计了对数据不做采样时得到的实验结果，得分最高的算法用粗体表示。从表2 中可以看出，所提方法在4 组数据集上平均AUC 值高于其他采样方法，且相较于SMOTE，AUC值平均提高了约1.6个百分点。

表2 不同方法的平均AUC对比结果 单位：%Tab.2 Average AUC comparison results of different methods unit:%

统计不同方法AUC和G-mean等评价指标下的平均排名，排名最高的算法均用粗体表示。如表3 所示，CHO 均取得了最高排名，表明该方法能够更有效地提升模型分类性能。图2 展示了各采样方法在CIC_Bot 和CIC_Inf 两个子数据上的平均AUC 并计算95%的置信区间。从图2 可以看出，CHO 对应的置信区间较窄，表明所提方法的性能是稳定的。

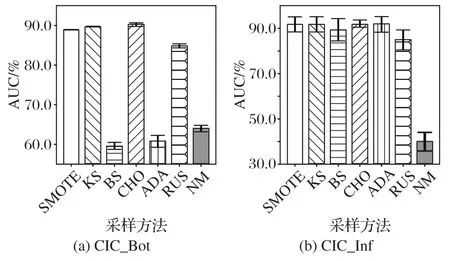
图2 不同方法的置信区间对比Fig.2 Comparison of confidence intervals of different methods

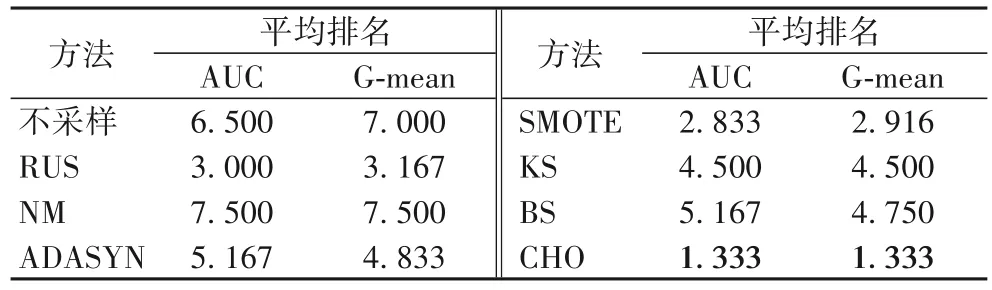
表3 不同方法的平均排名Tab.3 Average rankings of different methods

3.4 参数对方法性能的影响

接下来分析参数对所提方法性能的影响。多样性参数P的取值在0～1，值越大表示生成的数据多样性越强。分别计算P取值为0.1、0.3、0.5、0.7 以及0.9 时所提方法的分类性能。以CIC_Bot 和CIC_Infiltration 数据集为例进行实验，实验结果见图3。

从图3可以看出，对于CIC_Bot数据集，多样性参数取0.3时AUC值和G-mean值最高；而对于CIC_Inf数据集，多样性参数取0.3和0.5时得到的性能良好。考虑到P值过大，将选择高硬度样本进行采样，产生噪声的可能性也会增大，因此选择较小的P值是合适的。

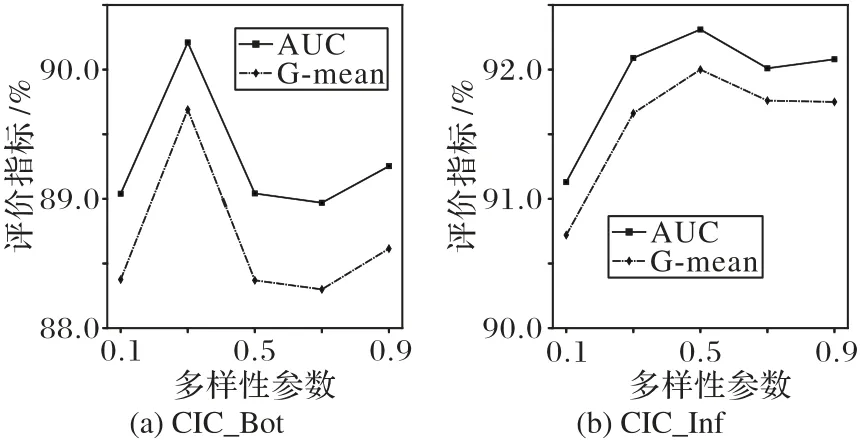
图3 多样性参数对不同评价指标的影响Fig.3 Influence of diversity parameter on different evaluation indexes

考虑到另一参数硬度数组V虽然和数据分布相关，但也可能受到近邻样本个数K的影响，分别取近邻个数为5、7、10计算硬度数组V，本文方法的评价指标结果见图4。由图4 可见，当K=10时，本文所提出的方法性能最好。

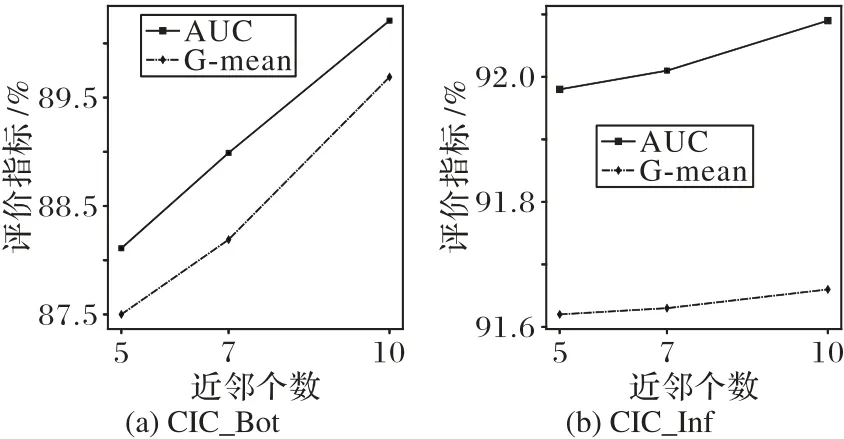
图4 近邻数对不同评价指标的影响Fig.4 Influence of neighbors’number on different evaluation indexes

对于大部分入侵检测数据集，CHO能取得比SMOTE等方法更好的性能，对于一些严重不平衡的数据如CIC_Bot、CIC_Inf，CHO 可以有效提高分类性能。实验还发现，过采样方法的性能明显优于不作采样。

3.5 结果分析

为了分析所提方法优于SMOTE 等方法的原因，通过一个二维数据进行直观的对比，并对实验中用到的部分入侵检测数据进行分析。

首先，通过一个二维数据对比不同方法的采样结果。由3.3节可知，SMOTE方法在所有方法中排名仅次于CHO，因此选择SMOTE进行对比。图5（a）展示了该数据的分布情况，可以看出存在两种颜色的数据，其中灰色和白色数据数量之比为2∶1，同时可看出右侧的白色数据分布更加离散。采用类似文献［16］中的方法评估数据的真实硬度，引入逻辑回归、决策树、朴素贝叶斯（Naive Bayes）和线性判别分析（Linear Discriminant Analysis，LDA）等分类器构成基分类器组G，进行5 次5 折交叉验证，将样本被误分类的分数作为该样本的硬度。

图5（d）则展示了数据中最初的硬度情况，黑色的样本表示高硬度的数据，所有分类器均无法正确分类这些数据。图5（b）则展示了SMOTE 扩充后的数据分布，可以看出SMOTE 生成的数据没有规律；而图5（e）则对应SMOTE 采样后数据的硬度情况，可以看出生成了噪声，加重了数据重叠。

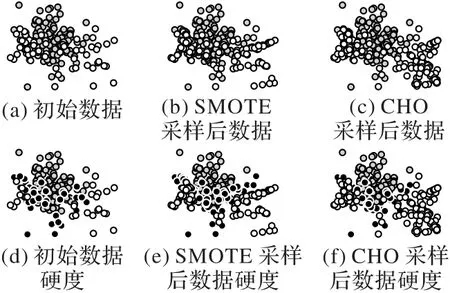
图5 不同方法采样结果和硬度情况对比Fig.5 Comparison of sampling results and hardness for different methods

图5（c）和图5（f）则展示了CHO 的采样结果和硬度情况。从图5（c）中可以看出，采样后的白色数据更加集中，生成的新数据基本保持在少数类数据范围内；对比图5（f）和图5（e），可以看出SMOTE产生了更多的高硬度点。

接下来，通过计算实例硬度分析入侵检测数据。仍以CIC_Bot 和CIC_Inf 这两个数据集为例，这两个数据集中的攻击流量分别对应僵尸网络和渗透攻击，且均为少数类。使用相同的方法计算数据的真实硬度，得到CIC_Bot 数据集的平均硬度为0.139，CIC_Inf 的平均硬度为0.005；并统计了数据集中正常流量和攻击流量的平均硬度，分别为0.298 和0.654，显著高于正常流量的平均硬度（0.138 和0.005 6），且硬度高于0.5 的攻击流量占总攻击流量的比例分别为17.5%和72.15%，而两个数据集中的正常流量平均硬度则偏低，这表明异常流量的分类难度显著大于正常流量。一种简单的采样方法是设置硬度阈值［5］，将硬度高于阈值的数据过滤掉，但是数据集中异常流量数据的硬度偏高，按照阈值过滤数据会严重损失信息。

类重叠是导致硬度偏高的主要因素［5］。当数据不平衡时，类重叠进一步影响分类器性能的提升。因此对于CIC_Bot和CIC_Inf 这两种严重不平衡的数据，攻击流量硬度值过高，表明数据重叠是非常严重的。使用SMOTE 等方法对数据过采样，将进一步加重类重叠，影响分类准确率。因此分别对CHO和SMOTE采样后得到的平衡数据再次计算平均硬度，结果见表4。

表4 不同方法的平均硬度对比Tab.4 Comparison of average hardness for different methods

从表4 可以看出，所提方法过采样后的数据平均硬度更低，表示重叠程度更小，分类难度更低，从而表明CHO 使分类器获得了更好的分类性能。

4 结语

在入侵检测中不平衡问题正变得越来越重要，近年来受到了相当多的关注。本文提出了一种基于聚类和实例硬度的入侵检测过采样方法处理入侵检测中的不平衡问题。该方法通过聚类和实例硬度确定安全区域，在安全区域中生成数据，并结合最优分配原理，改进传统过采样方法的缺点，在6 组网络安全数据集上进行对比实验。实验结果表明，所提CHO 与其他采样方法相比，具有更好的性能。在接下来的工作中，可尝试向基于采样的分类器集成的方向进行拓展研究，进一步提高入侵检测中机器学习模型的性能。