基于云雾计算的可追踪可撤销密文策略属性基加密方案

陈家豪，殷新春，2*

（1.扬州大学信息工程学院，江苏扬州 225127；2.扬州大学广陵学院，江苏扬州 225128）

（∗通信作者电子邮箱xcyin@yzu.edu.cn）

0 引言

云计算［1］的广泛应用使得用户能够以较低的成本存储和共享数据。然而，随着网络边缘设备数量的迅速增加，这些设备产生的数据量越来越大，集中的云服务器已经不能高效地处理边缘设备产生的海量数据。雾计算［2］是对云计算的延伸，它是在边缘设备和远端云之间再扩展的一层，也可以叫作边缘网络层。在物联网应用中有些请求的处理不需要放到远端的云，而是可以直接在距离边缘设备较近的雾端进行处理。雾计算将云提供的服务扩展到网络边缘来提供本地化的服务，这有效满足了边缘设备对低时延、移动性支持、位置感知的服务需求。Statista 的报告［3］显示，全世界的雾计算规模将在2022年达到130亿美元。

为了充分利用雾计算技术，Stojmenovic 等［4］引入了云雾设备（cloud-fog-device）体系来提供各种应用服务，包括智能城市、智能电网、智能交通和工业自动化。在该体系中，数以千计的云被用来存储数据；数百万个雾节点被用来减少数据传输期间的工作负载和带宽；数十亿个边缘设备用于请求和上传数据。其中，雾节点在维护高速缓存的数据方面发挥着重要作用，并为数据的智能处理提供了协同合作。雾节点的目的是帮助边缘设备克服资源限制，以减少数据传输期间的带宽成本。以智能交通为例，云雾设备体系实现了应用服务器与车辆之间的高效数据通信。具体而言，云从应用服务器接收消息，并转发到相应的雾节点，雾节点将消息传送到终端设备。

然而，云雾计算并不是完全可信的，如果不能很好地解决其中的安全和隐私保护问题，那么这将严重阻碍云雾计算的发展［5-8］。Stojmenovic 等［4］指出，雾节点在分发身份验证信息和收集审核日志时，与远程云的连接不稳定，因此容易遭受中间人攻击。这种脆弱的连接降低了在远程云服务器上执行身份验证协议的可靠性。Huang 等［7］随后引入了一种带有独立身份验证（Stand-Alone Authentication，SAA）的新机制，以实现用户身份验证从而适应不稳定的连接情况。但是，要采用SAA，需要保护雾节点与用户之间的身份验证信息，这又带来了额外的存储开销。数据加密是进行安全数据共享的常用方法，但是在传统的云雾计算中，基于公钥基础设施的身份验证困难且效率不高。属性基加密（Attribute-Based Encryption，ABE）［9-11］机制能克服这一障碍，它无需事先知道数据接收者的具体身份，却能够实现灵活的一对多加密，同时能实现对数据的细粒度访问控制。Sahai 等［9］首次提出了ABE 机制。随后Goyal 等［10］首次提出了基于密钥策略的属性基加密（Key-Policy Attribute-Based Encryption，KP-ABE）方案，其中在密钥中指定访问策略，在密文中指定属性集合，只有当密文的属性集合满足密钥所指定的访问策略时才能解密。Bethencourt等［11］首次提出基于密文策略的属性基加密（Ciphertext-Policy Attribute-Based Encryption，CP-ABE）方案，与KP-ABE 构造相反，它在密文中指定访问策略，在密钥中指定属性集合，只有当密钥的属性集合满足密文指定的访问策略时才能解密。因为CP-ABE 方案不仅可以对数据共享进行细粒度的访问控制，而且数据加密者可以定义访问策略，所以CP-ABE 得到了更广泛的应用。

虽然属性基加密具有广阔的应用前景，但是在实际应用中，存在恶意用户将解密密钥泄漏给ABE 系统中的第三方的情况。由于解密密钥与属性相关联，因此无法确定泄漏解密密钥的用户。例如，Alice 拥有属性集｛计算机系，教授，女性｝而Bob 拥有属性集｛计算机系，教授，男性｝。假设根据访问策略｛计算机系and 教授｝生成一条密文，由于Alice 和Bob 都具有相同的属性子集｛计算机系，教授｝，他们都能够解密这个密文，如果解密密钥泄露，则无法确定是Alice 还是Bob 泄漏了密钥。为了解决恶意用户密钥泄露的问题，Liu等［12］提出了第一个白盒可追踪CP-ABE 方案，接着，Ning 等［13-14］提出了两个白盒可追踪CP-ABE 方案，它们分别支持大属性空间和灵活的属性集。尽管上述方案能够追踪到恶意用户，但无法有效地撤销他们的访问权限。为满足这一实际要求，文献［15-18］提出了许多可撤销的基于属性的加密（Revocable Attribute-Based Encryption，RABE）方案。目前主要有两种撤销机制:间接撤销和直接撤销。对于前者，属性权威机构需要与未撤销的用户通信并发送更新信息，系统中存在大量用户时，这将导致大量的通信开销。而对于后者，用户不必与更新撤销列表的属性权威机构进行通信。高嘉昕等［16］提出了一个支持属性撤销的可追踪外包属性加密方案，其中属性撤销需要利用重加密方法更新用户密钥，这导致了大量的通信开销。明洋等［18］提出了一个支持直接撤销的可验证外包的属性加密方案，该方案为每个属性引入了版本密钥，增加了用户的存储开销，且该方案只实现了属性层面的撤销，并未对用户层面进行撤销。目前，文献［19-23］提出了许多可直接撤销的属性基加密方案。Shi等［22］提出了一个有效的撤销方案，其中数据服务管理者只需更新与最新撤销列表R'相关的部分密文。但Shi等［22］只是专注于KP-ABE的撤销，且不支持外包解密。

为了解决上述问题，本文提出了一个在云雾环境下的支持用户撤销的可追踪可外包解密的密文策略属性基加密方案。本文的主要工作如下:

1）支持恶意用户的追踪和撤销。在本文的方案中，解密密钥分为两部分:一部分与属性集相关，另一部分与二叉树中叶子节点存储的用户身份有关，与Liu 等［12］的方案相比，本文方案不需要额外的身份列表来存储用户的身份。密文分为两部分:一个与访问策略相关，另一个与撤销列表相关。在解密密钥泄露的情况下，可以从解密密钥中追踪到该用户的身份，并将其添加到撤销列表中，以此来撤销其访问权限。

2）支持雾计算与外包解密。本文方案针对实际应用中边缘设备计算能力不足、通信延时较大等缺陷，在云计算技术和传统的属性基加密的基础上，加入了雾计算与外包解密技术。在本文中，雾节点与云服务器进行通信，而边缘设备只需与本地雾节点进行通信，从而能有效降低设备的通信延时与响应时间。同时，利用雾节点进行外包解密，能够显著减少解密的计算量，提高边缘设备的解密效率。

安全性分析表明，本文方案在判定性q-BDHE（decisionalq-Bilinear Diffie-Hellman Exponent）假设下是 IND-CPA（INDistinguishability Chosen-Plaintext Attack）安全的，且在l-SDH（l-Strong Diffie-Hellman）假设下可抵抗密钥伪造攻击。性能分析表明，本文所提的方案在系统功能和计算开销方面相较其他方案更具有优势。

1 预备知识

1.1 符号介绍

本文方案中使用到的一些符号的定义如表1所示。

表1 相关符号及定义Tab.1 Related notations and their definitions

1.2 双线性映射

令G和GT是两个阶为素数p的乘法循环群，g是G的一个生成元。存在一个双线性映射e:G×G→GT，满足如下性质:

1）双线性性:∀u，v∈G，∀a，b∈Zp，有e(ua，vb)=e(u，v)ab。

2）非退化性:e(g，g) ≠1。

3）可计算性:对∀u，v∈G，都存在有效算法去计算e(u，v)。

1.3 访问策略

设{P1，P2，…，Pn}为n个参与者的集合。对于集合如果 ∀B，C⊆{P1，P2，…，Pn}，B∈C，B⊆C⇒C∈A，则称集合A是单调的。其中属于A的集合称为授权集；否则，称为非授权集［24］。

举例来说，对于{A，B，C，D}，单调集合{{A，B}，{B，C}，{C，D}，{A，B，C}，{A，B，D}，{A，C，D}，{B，C，D}}就是一个单调访问策略，{A，B}，{B，C}，{C，D}是三个授权集合，而{A，D}则是一个非授权集合。通常来说，单调访问策略可以表示成不包含“非”的布尔公式；非单调的访问策略，可以用包含“非”的布尔公式来表示。

1.4 线性秘密共享方案

令V 表示属性全集，p表示一个素数。秘密空间Zp上的秘密共享方案Π，实现了V 上的访问策略。如果秘密分享方案Π满足以下两个性质［23］，则Π是线性的。

1）秘密s∈Zp分割成的每一个部分对应了V 中的一个属性，且每个部分构成Zp上的一个向量。

2）对于访问策略S=(M，ρ)，M是一个l×n的秘密分享矩阵。函数ρ将M的第i∈{1，2，…，l}行映射到全集V的一个属性ρ(i)。通过这样的映射，矩阵M的每一行都代表V 上的一个属性。例如，构造一个列向量u=(s，y2，y3，…，yn)T，其中y2，y3，…，yn∈Zp是随机数，用于隐藏要共享的秘密值s。则是l行1列的向量，也就是把秘密值s根据Π 分成了l个部分。(Mu)i对应属性ρ(i)，其中i∈[l]。

如文献［24］中所示，符合以上定义的线性秘密共享方案（Linear Secret Sharing Scheme，LSSS）可以进行线性重构算法Recon。Recon 的具体定义如下:Π 为访问策略S上的线性秘密共享方案，P∈S为任意授权集合，集合I={i∈[l]∧ρ(i)∈P}且I⊆{1，2，…，l}。对于秘密s的任意合法分享{λi=(Mu)i}i∈I，存在常量集合{σi∈Zp}i∈I可以在多项式时间内计算出来。而对于非授权集合p'，则不存在{σi}i∈I这样的常量集合。

1.5 二叉树

令U为系统中的用户集合，R为撤销列表，则在二叉树［25］中定义:

1）一个二叉树T 的叶子节点只关联一个用户。令root为根节点，|U|为用户数，则树中的节点数为2|U|-1，使用宽度优先搜索为树中节点编号。例如，根节点为1，最后一个节点为2|U|-1。

2）path(i)定义为从根节点到节点的路径。

3）最小包含集合cover(R)是所有未在撤销列表内的用户的最小集合［26］。令ui为撤销列表R中的用户，xl和xr分别为x节点的左右孩子节点，定义一个可以以最少节点表示不在R中节点的算法使得cover(R)=Covernodes(T，R)，其中Covernodes(T，R)定义如算法1所示。

4）若一个用户不在撤销列表中，则存在一个唯一的节点j=cover(R) ∩path(u)。

如图1所示，撤销列表为R={u5，u8}={11，14}，所以cover(R)={1，12，13}。已知u3的路径path(u3)=path(9)={0，1，4，9}，因此这个唯一的节点j=cover(R)∩path(u8)={1}。

图1 二叉树Fig.1 Binary tree

算法1Covernodes。

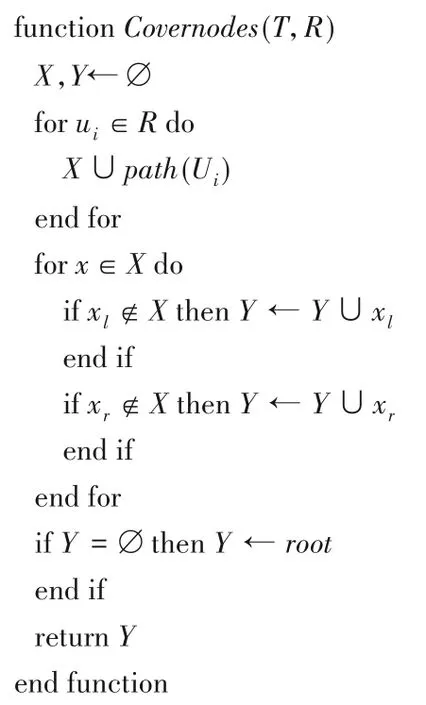
1.6 复杂性假设

q-BDHE（q-Bilinear Diffie-Hellman Exponent）假设［27］:选取阶为素数p的乘法循环群G和GT，g是群G的生成元，e为双线性映射e:G×G→GT，随机选取d，s∈Zp，随机选取F∈GT。给定y=令，F为GT中的随机元素，如果|Pr [B(y，T=Pr [B(y，T=F)=0]|≥ε，即B能够在多项式时间内区分T和F，则称B能以优势ε解决q-BDHE假设。

定义1若不存在一个算法可以在多项式时间内以不可忽略的优势解决q-BDHE问题，则称q-BDHE假设成立。

l-SDH（l-Strong Deffie-Hellman）假设［19］:选取阶为素数p的乘法循环群G，g是群G的生成元，随机选取x∈Zp。给定一个l+1元组作为输入，输出一个配对如果(c，g1/(c+x))]|≥ε，即B能够正确输出配对则称B能以优势ε解决l-SDH假设。

定义2若不存在一个算法可以在多项式时间内以不可忽略的优势解决l-SDH问题，则称l-SDH假设成立。

2 系统和安全模型

在本文中，考虑如下应用场景。某地的汽车销售服务公司（以下简称公司）为其售出的车辆提供基于云雾计算的数据共享服务。为了实现细粒度的访问控制和支持一对多的通信模式，公司需要为加密数据制定灵活的访问策略。在该项服务中，每个车辆会被分配一系列属性，如｛“2014 年生产”，“A品牌”，“SUV”｝。作为一种强大的“一对多”加密机制，密文策略属性基加密（CP-ABE）非常适合该应用场景。出于安全考虑，发送方需要先使用CP-ABE 技术加密其信息，然后再上传至本地的雾节点，雾节点分析密文是否有长期用途（longterm），如果密文有长期用途，则由雾节点上传至云服务器（以分担雾节点存储压力），否则存在本地或者转发给其他雾节点。如公司需要召回一批2014 年生产的A 品牌的运动型多用途汽车（Sport Utility Vehicle，SUV），这批车辆的刹车存在重大安全隐患，为了保障用户隐私安全同时避免此安全隐患被不法分子获悉，公司需要加密消息并嵌入访问策略为“2014年生产∧A 品牌∧SUV”，以确保只有满足此访问策略的车辆才能解密该密文。此密文有长期用途，由公司上传至本地雾节点并由雾节点上传至云服务器。若该公司为了答谢客户，准备在“双十一”举办一个限时优惠活动。为了确保目标客户能够接收到消息且该消息不被其他汽车保养公司所获得，该公司需要加密消息并嵌入访问策略为“B品牌∧轿车”，以确保只有满足此访问策略的车辆才能解密该密文。此密文仅有短期用途（short-term），由发送方上传至本地雾节点并存储，若本地雾节点存储能力不够，则将此消息发送给相邻的雾节点存储。只要车辆的属性满足密文中嵌入的访问策略，则由雾节点先进行密文的外包解密，之后将半解密密文发送回车辆，车辆利用自己的密钥解密从而获得明文。

2.1 系统模型

本文方案的系统模型一共包含5个部分，如图2所示:

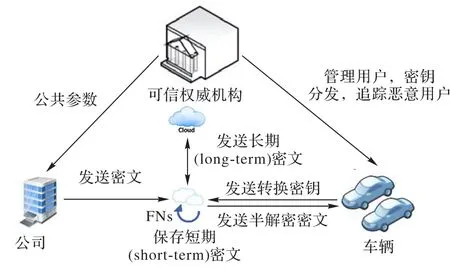
图2 本文方案的系统模型Fig.2 System model of proposed scheme

1）可信权威机构负责生成系统公共参数和主私钥，还负责车辆的注册、密钥分发。一旦发现有密钥被泄露，可信权威机构就调用跟踪算法对该密钥进行追踪，找到泄露解密密钥的恶意用户，并将恶意用户的身份加入撤销列表中。

2）车辆是资源受限的设备，主要进行以下工作:

①车辆向本地雾节点请求相关密文。

②车辆将需要分享的数据进行加密并且传送给本地雾节点。

3）公司根据可信权威机构发布的公共参数和撤销列表，制定相应访问策略，并将消息加密后传送给雾节点。

4）雾节点（Fog Node，FN）是边缘服务器，负责以下工作:

①FNs充当高速缓存，存储具有短期目的的数据和信息。

②FNs将具有长期目的的数据转发到云服务器。

③在从车辆接收数据查询之后，FNs 首先搜索本地存储并与其他FNs 进行交互。如果请求不到查询的密文，则FNs向云服务器请求密文。

值得注意的是，尽管允许车辆与云服务器直接通信，但是由于云服务器存在远端而FNs 在实际情况下更接近车辆，因此车辆与云服务器直接通信会占用更多带宽。

5）云服务器（Cloud Server，CS），具备大量存储空间，可以容纳数据，还可以通过公共通道将加密的数据共享给FNs。

2.2 形式化定义

本文方案主要由以下6 个算法组成，分别是系统初始化算法Setup、加密算法Encrypt、用户密钥生成算法KeyGen、外包解密算法Transform、解密算法Decrypt 和追踪算法Trace。各算法分别定义如下:

1）Setup(λ，A，T) →(PP，MSK，R，List):该算法由可信权威机构执行，算法的输入为安全参数λ、属性全集A和二叉树T，输出系统公共参数PP和主私钥MSK，并将PP公开。可信权威机构还初始化一个空的撤销列表R和一个空的追踪列表List。

2）Encrypt(PP，m，(M，ρ)，R) →CT:该算法由发送者执行，算法输入公共参数PP、要发送的明文消息m、一个LSSS访问策略(M，ρ)和撤销列表R，输出密文CT。

3）KeyGen(MSK，u，S) →SK:该算法由可信权威机构来执行，算法输入主私钥MSK、用户身份u、用户属性集S，输出用户密钥SK，并将SK发送给车辆。SK包含两部分，分别是用户转换密钥TK与用户个人密钥UK。

4）Transform(CT，TK) →CT':该算法由雾节点执行，该算法输入密文CT和用户转换密钥TK，输出半解密密文CT'，并将CT'发送给车辆。

5）Decrypt(UK，CT') →m:该算法由接收者执行，输入用户个人密钥UK和半解密密文CT'，输出明文m。

6）Trace(PP，R，SK) →uoru∅:该算法由可信权威机构执行，输入公共参数PP、撤销列表R、用户密钥SK，如果追踪到了恶意用户，则输出该用户的身份u，否则输出u∅。

2.3 密钥伪造攻击安全模型定义

本文采用文献［28］定义的密钥伪造攻击模型，其中密钥伪造攻击定义可以通过一个挑战者B和一个攻击者Adv之间的安全游戏来描述，具体步骤如下所示:

1）初始化:挑战者B运行Setup 算法，并将公共参数PP发送给攻击者Adv。

2）密钥询问:攻击者Adv向挑战者B询问与属性集(u1，S1)(u2，S2)…(uq，Sq)相关的用户密钥，其中ui∈R或者SI∉(M，ρ)，i=1，2，…，q。B运行KeyGen 算法并返回相应的密钥。

3）密钥伪造:攻击者Adv输出一个用户密钥SK*。如果Trace(PP，R，SK*)≠⊥，并且Trace(PP，R，SK*)∉{id1，id1，…，idq}，其中idi(i=1，2，…，q)为用于询问的用户身份，攻击者Adv赢得上述游戏。

攻击者Adv赢得上述游戏的优势定义为:

ε=Pr [Trace(PP，R，SK*)∉{ ⊥，id1，id2，…，idq}]。

定义3若不存在多项式时间攻击者能以不可忽略的优势赢得上述游戏，那么称本文提出的方案是可抵抗密钥伪造攻击的。

2.4 选择明文攻击安全模型定义

本文采用文献［27］定义的安全模型，该模型定义为挑战者B与攻击者Adv之间交互的安全游戏，该游戏是选择明文攻击（Chosen Plaintext Attack，CPA）下的不可区分性（INDistinguishability，IND）游戏。具体描述如下:

1）初始化:攻击者Adv选择要挑战的一个访问策略(M*，ρ*)并将其发送给挑战者B，其中M*是一个l*×n*的矩阵，函数ρ*把矩阵M*的一行映射成一个属性ρ*(i)。

2）系统建立:挑战者B运行Setup 算法，将公共参数PP发送给攻击者Adv。

3）阶段1:攻击者Adv向挑战者B询问与属性集(u1，S1)(u2，S2)…(uq，Sq)相关的用户密钥。

①若Si⊨(Μ*，ρ*)且ui∉R*，则不做处理。

②若S⊭(M，ρ) 或ui∈R*，挑战者B生成一个与属性(ui，Si)相关的用户转换密钥，并将它发送给攻击者Adv。

4）挑战:攻击者Adv向挑战者B提交2 个等长的消息m0和m1。挑战者掷一枚均匀的硬币η∈{0，1}，并在访问策略(Μ*，ρ*)和撤销列表R*下加密mη生成挑战密文CT*。挑战者B将CT*发送给攻击者Adv。

5）阶段2:阶段2重复阶段1的步骤。

猜测:攻击者Adv输出对η的猜测η'，若η=η'，则攻击者Adv赢得游戏。

攻击者Adv赢得上述游戏的优势定义为:

ε=|Pr [η'=η]-1/2|

定义4若不存在多项式时间攻击者能以不可忽略的优势赢得上述游戏，那么认为本文提出的方案是IND-CPA 安全的。

3 本文方案

3.1 方案工作流程

本文方案可分为4个阶段:

1）系统初始化。可信权威机构运行Setup 算法生成公共参数PP，并将PP发送给各个实体。可信权威机构运行KeyGen算法为每个用户生成密钥SK，并通过安全信道发送给车辆。

2）数据上传。数据发送者将数据加密并上传至本地雾节点。FNs 分析密文是否具有长期用途，若密文仅有短期用途，则FNs将此密文存储在本地，若本地节点存储容量不够，则将此密文转存至相邻的FNs。若密文具有长期用途，FNs将密文上传至云服务器保存。

3）数据下载。当车辆向本地FNs请求密文时，FNS首先在本地寻找符合要求的密文，如果没有找到，则此FNs 向其他FNs 与CS 请求密文，雾节点将获取到的密文进行外包解密，并将半解密密文发送给车辆，由车辆进行最终解密。

4）恶意用户追踪与撤销。在用户密钥泄露的情况下，可信权威机构可以从该密钥中追踪到恶意用户的身份，并将其添加到撤销列表中，以此来撤销其访问权限。

3.2 方案构造

本节主要展示方案的具体构造并对相关参数进行说明。在本文的方案中，二叉树用于实现追踪和撤销，用户密钥分为两个部分:一部分与用户的身份有关，另一部分与用户的属性集有关。密文包含两个部分:一部分与撤销列表相关，另一部分与访问策略相关。当且仅当用户密钥中的属性满足密文中的访问策略并且用户身份不在撤销列表中时，该用户才能解密密文。具体方案如下:

1）Setup(λ，A，T) →(PP，MSK，R，List)。

Setup 算法由可信权威机构执行，算法的输入为安全参数λ、属性全集A和二叉树T，输出系统公共参数PP、主私钥MSK、撤销列表R和追踪列表List。该算法选取阶为p的循环群G和GT，G的生成元为g，e:G×G→GT为双线性映射。U为用户集合，R是一个撤销列表（初始化为空），List是一个追踪列表（初始化为空），T 是一个满二叉树，树上的每一个叶子节点分别对应一个用户u，树的深度为d。因此用户数目最多为|U|=2d，树中的节点数为2|U|-1。算法做如下运算:

①随机选取α，α∈Zp，h∈G，一个抗碰撞的哈希函数H:{0，1}*→G。

②对∀x∈A，选择Ax∈G。

③对树中的每一个节点，在Zp中随机选取X={xi}i∈[2|U|-1]，计算Y=

系统按照以下格式公布公共参数(PP)并保存主私钥和追踪列表(MSK，List):

PP=(g，h，e(g，g)α，ga，H，R，(Ax)x∈A，A)

MSK=(α，a，X)

List=∅

2）Encrypt(PP，m，(M，ρ)，R) →CT。

Encrypt 算法由公司执行，算法输入公共参数PP、撤销列表R、要发送的消息明文m和访问策略(M，ρ)，输出密文CT。其中M是一个l×n的矩阵，函数ρ把矩阵M的一行映射成一个属性ρ(i)。随机选择s，v2，v3，…，vn∈Zp，并设置向量μ=(s，v2，v3，…，vn)T，其中s是用于分享的随机秘密值。对所有的i=1，2，…，l，计算λi=Mi×μ，其中Mi表示矩阵M的第i行。

①首先，设置如下与访问策略关联的部分密文:

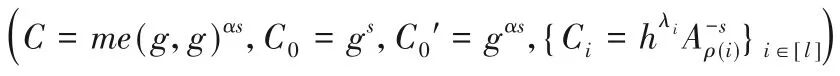
②对∀j∈cover(R)，有path(j)={i0，i1，…，idept(j)}，其中i0=root，idept(j)=j。然后，设置如下与撤销列表R相关的部分密文:

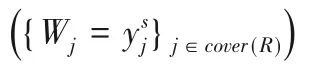
③最后构成完整的密文如下:

CT=(C，C0，C0'，{Ci}i∈[l]，{Wj}j∈cover(R)，(M，ρ)，R)

3）KeyGen(MSK，u，S) →SK。

KeyGen 算法由可信权威机构来执行，算法输入主私钥MSK，身份u，用户属性集S，输出用户密钥SK，SK由用户转换密钥TK与用户个人密钥SK组成。随机选择r，t，z∈Zp。计算c=H(id)，其中id是与用户u相关联的叶子节点的值，然后把二元组(c，id)加入列表List。

①首先，设置如下与用户属性集相对应的部分密钥:

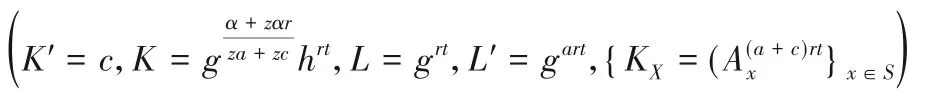
②令path(id)={i0，i1，…，id}，i0=root，id是与用户u相关联的叶子节点。随机选取b∈Zp，设置与用户身份u关联的部分密钥，如下所示:

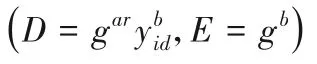
③用户转换密钥TK与用户个人密钥UK如下所示:

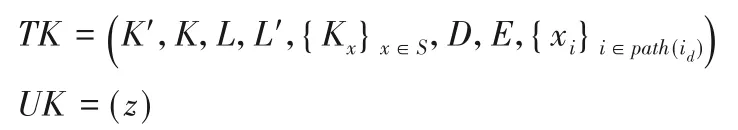
④最后构成完整用户密钥如下:

SK=(TK，UK)

4）Transform(CT，TK) →CT'。

Transform 算法由雾节点执行，该算法输入密文CT和用户转换密钥TK，输出半解密密文CT'。该算法的输出存在以下两种情况:

情况1 若用户的身份u∈R或者用户属性集S不满足密文的访问策略(M，ρ)，算法输出⊥。

情况2 若用户身份u∉R且用户属性集S满足密文的访问策略(M，ρ)，算法执行如下运算:

①因为u∉R，所以存在一个节点j=cover(R) ∩path(u)。令path(j)={i0，i1，…，idept(j)，…，id}，其中，idept(j)=j，id是与用户u相关联的叶子节点。计算

②对于S∈(M，ρ)，令I={i:ρ(i)∈S}⊆{1，2，…，l}，存在{ci|i∈I}使得{ciMi=(1，0，…，0)}，因此，有

③最终，计算:

系统输出半解密密文CT'。

5）Decrypt(UK，CT') →m。

Decrypt 算法由车辆执行，输入半解密密文CT'和用户个人密钥UK，输出明文m:

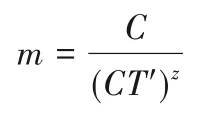
6）Trace(PP，R，SK) →uoru∅。

Trace 算法由可信权威机构执行，输入公共参数PP，撤销列R，用户密钥SK，输出跟踪到的恶意用户u或u∅。

若用户密钥SK符合以下三个检测:

1）K'∈Zp，K，L，L'，Kx，D，E∈G。

2）e(g，L')=e(ga，L) ≠1。

3）∃x∈S，s.t.e(Ax，LK'L)=e(g，Kx)≠1。

那么用户密钥SK是完整的，否则算法直接输出符号⊥表示密钥不完整，无法进行追踪。对于通过上一步完整性检查的用户密钥，算法在列表List中根据密钥中的K'查找对应的用户u。如果找到了K'，算法输出K'对应的id，该用户就是被追踪的恶意用户，并将其身份u加入撤销列表R；否则，输出u∅表示没有查找到恶意的用户。

4 安全性分析

4.1 密钥伪造攻击

定理1令q为攻击者Adv查询密钥的次数，若l-SDH 困难性假设成立，则方案在q＜l的情况下是可抵抗密钥伪造攻击的。

证明 假设存在一个多项式时间的攻击者Adv在经过了q(l=q+1)次密钥查询之后可以以不可忽略的优势ε赢得密钥伪造攻击游戏。那么能够构造一个概率多项式时间算法B以不可忽略的优势攻破l-SDH 困难性假设。选取阶为p的乘法循环群G和GT，G的生成元为g，e:G×G→GT为双线性映射，g1∈G，a∈Zp。给出实例B的目标是输出cr∈Zp和wr∈G并满足，从而解决l-SDH 假设。令Ai=B以挑战者的身份与Adv进行密钥伪造攻击游戏。

1）初始化。B随机选取q个不同的值c1，c2，…，cq∈Zp，随机选取α，θ∈Zp，u∈G。令多项式f(y)=展开f(y)，可以得到形如f(y)=的表达式，其中αi∈Zp(i=0，1，…，q)，是多项 式f(y) 展开式中各项的系数。B计算g和ga:

对每一个属性x∈A，随机选取ux∈Zp，令。对二叉树T中的每个节点，在Zp中随机选取X={xi}i∈[2|U|-1]，计算i∈[2|U|-1]。公共参数如下所示:

PP=(g，h，e(g，g)α，ga，H，(Ax)x∈A，Y)

2）密钥询问。Adv提交(ui，Si)给B，询问用户ui的密钥SKi。假设这是Adv的第i次询问(i≤q)。令多项式fi(y)=B计算，然后B随机选取t，r∈Zp并计算:K'=ci，K=(σi)α/z+αrhrt，L=grt，L'=(ga)rt，令path(ui)={i0，i1，…，id}，其中i0=root，id是与用户ui相关联的叶子节点。B随机选择b∈Zp，令，E=gb。最终B将密钥SKi=(K'，K，L，L'，，D，E，发送给Adv。SKi表示Adv第i次询问得到的用户密钥。

3）密钥伪造。Adv将用户密钥SK*提交给B，令εA表示Adv赢得密钥伪造攻击游戏。即SK*满足用户密钥格式检查的3个条件，并且K'∉{c1，c2，…，cq}。存在以下两种情况:

①假设εA未发生，则不作处理。

②假设εA发生了，B设置一个多项式f(y)=γ(y)·(y+K')+γ-1，其中γ(y)=且γ-1∈Zp，由于(y+ci)，ci∈Zp，K'∉{c1，c1，…，cq}，即(y+K')不能整除f(y)。假设L=grt（r，t∈Zp且未知），可以得到L'=gart。根据e(LK'L'，Λ)=e(L，gα)，得到Λ=，令:

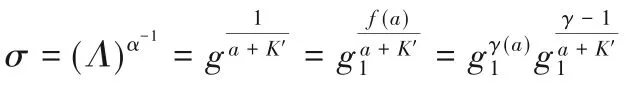
B计算一个二元组(cr，wr)如下所示:

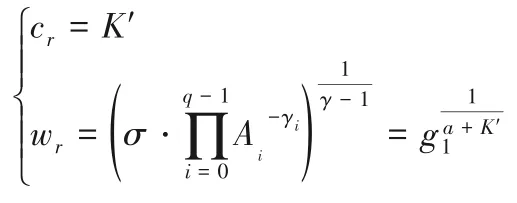
以下论证B攻破l-SDH 困难性假设的优势。令ξ表示(cr，wr)是l-SDH 挑战问题的解决方案，可以通过检查wr)=e(g1，g1)是否成立来进行验证。当B随机选择(cr，wr)时，ξ的发生概率可以忽略不计。在(Adv·wins∧gcd(γ-1，p)=1)的情况下，(cr，wr)满足=e(g1，g1)的概率为1。当B输出(cr，wr)时，假设Adv赢得游戏的概率为ε。

所以，B以如下概率赢得了l-SDH游戏:

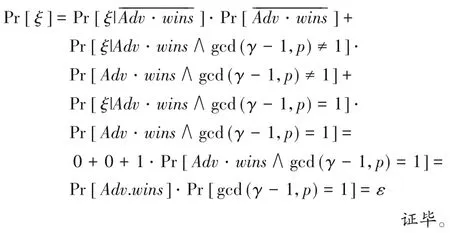
4.2 IND-CPA安全性分析

定理2假设判定性q-BDHE 困难性假设成立，那么在选择访问策略和选择明文攻击下，不存在多项式时间的攻击者Adv能以不可忽略的优势攻破本文的系统（q＞2|U|-1，|U|是系统中用户个数）。

证明 如果存在一个多项式时间攻击者Adv能以优势ε攻破本文的系统，那么本文能创建一个挑战者B以优势ε/2解决q-BDHE 问题。选取阶为p的乘法循环群G和GT，G的生成元为g。令e:G×G→GT为双线性映射。证明过程如下:

1）初始化。Adv选择一个要挑战的访问策略(M*，ρ*)，其中M*是一个l*×n*的矩阵，n*≤q。

2）系统建立。B执行如下操作:

①选择α∈Zp使得e(g，g)α=·e(g，g)α'，由此可得α=α'+dq+1。

②对x∈[|U|]，随机选择一个值zx∈Zp。每个组元素Ux∈G定义如下。

若存在i∈{1，2，…，l*} 使得ρ*(i)=x，令Ux=。

若不存在i∈{1，2，…，l*}使得ρ*(i)=x，令Ux=。

③随机选取a∈Zp，计算ga，令h=gd。

④给定撤销列表R*，令={i∈path(u)|u∈R*}。每个组元素yi∈G(i=1，2，…，2|U|-1)定义如下:

若i∈IR*，随机选取vi∈Zp，令yi=，令xi=di+vi；否则，令，令xi=dq+vi。

公共参数如下所示:

PP=(g，h，e(g，g)α，ga，H，(Ax)x∈A，Y)

3）阶段1。在本阶段，Adv向B询问与一系列与(u，S)相关的用户密钥。

情况1 如果S⊨(Μ*，ρ*)且ui∉R*，则不作处理。

情况2 如果S⊨(M，ρ)或ui∈R*，B随机选取r，c∈Zp并计算K'，K，L，L'，Kx。

path(u)={i0，i1，…，id}，其中i0=root，id是与用户u相关联的叶子节点。由于u∈R*，可以得到和，k=0，1，…，d，因此。B选取b'∈Zp，并计算D、E。

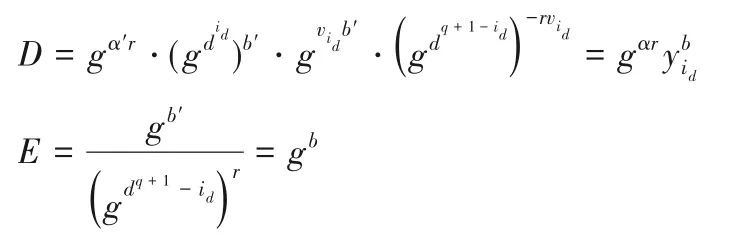
情况3 如果S⊭(M*，ρ*)且ui∈R*，B进行如下运算:

①令I={i:ρ*(i)∈S}⊆{1，2，…，l}，ω1=-1，存在向量使得

②随机选取r，c∈Zp，令K'=c。

③随机选取β∈Zp，令:

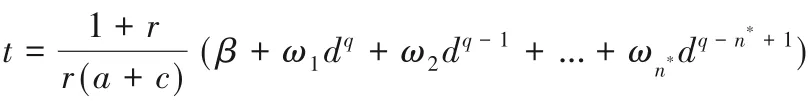
④计算L，L'，K。

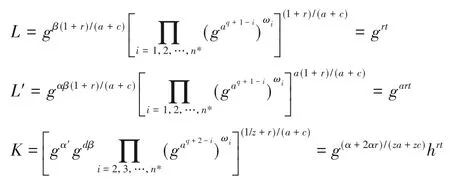
⑤对∀x∈S，计算Kx。若不存在i使得ρ*(i)=x，令Kx=；否则，存在i，使得ρ*(i)=x，设置Kx如下:

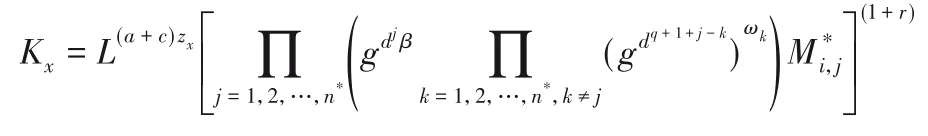
⑥按照情况2的步骤计算D、E。

情况4 如果S⊭(M*，ρ*)且ui∉R*，B按照情况3 的步骤计算K'，K，L，L'，Kx，假设path(u)={i0，i1，…，id}，其中i0=root，id是与用户u相关联的叶子节点。由于u∉R*，则ik∉和=dq+vi，k=0，1，…，d。因此。B随机选取b'∈Zp并计算D、E。

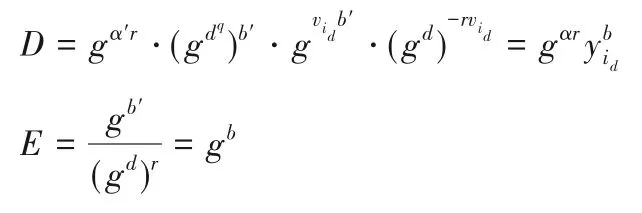
4）挑战。Adv向B提交2 个等长的消息m0，m1，B做如下运算:

①B掷一枚均匀的硬币η∈{0，1}并计算Cη，C0，C0':

Cη=mη·W·e(gs，gα')

C0=gs

C0'=(ga)s

②随机选取r2'，r3'，…，rn*'∈Zp，并计算v。

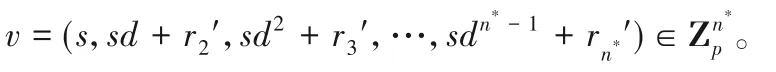
③计算Ci=

④对∀j∈cover(R*)，定义path(j)={i0，i1，…，idepth(j)}，i0=root，idepth(j)=j。由于∀j∈cover(R*)，可得xj=aq+，yj=令Tj=

最终，B输出密文CT并将它发送给Adv。

CT=(Cη，C0，C0'，{Ci}i∈[l]，{Wj}j∈cover(R))。

5）阶段2。阶段2重复阶段1的步骤。

6）猜测。Adv输出对η的猜测η'，若η'=η，B输出对v的猜测v'=1；否则，B输出对v的猜测v'=1。

①当v=0 时，Z=且Adv获取到了一个合法的密文。假定Adv的优势ε=Pr [η=η'|v=0]-由于Pr [η=η'|v=0]=Pr [v=v'|v=0]，因此B赢得游戏的概率是Pr [v=v'|v=0]=ε+

②当v=1时，Z是GT中的随机元素，因此，Adv无法获得η的任何信息。在此情况下，Adv没有任何优势，所以Pr [η≠η'|v=1]=由于Pr [η≠η'|v=1]=Pr [v=v'|v=1]，因此B赢得游戏的概率是Pr [v=v'|v=1]=

最终，B解决q-BDHE困难性假设的总体优势为:

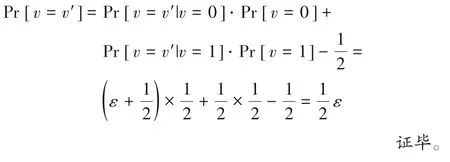
5 方案对比

对本文方案和文献［22］方案、文献［29］方案、文献［30］方案、文献［31］方案、文献［32］方案的功能和效率进行了评估和比较，由于此5 个方案与本文方案在系统功能上有部分相似点，故选择此5 个方案进行对比。具体对比情况如表2～3所示。

在表2 中，进行了功能的对比，其中文献［22］方案提出了一个可追踪的属性基加密方案。然而，该方案仅支持密钥策略属性基加密，且未实现用户撤销与外包解密的功能。文献［29］方案虽然支持用户的撤销，与本文方案相比，文献［29］方案仅通过密钥更新来实现撤销，发生撤销时，需要更新所有未被撤销的用户的密钥，这增加了系统的计算开销与通信开销。文献［30］方案实现了支持外包解密的属性基加密方案，但没有实现用户追踪，当用户泄露自己的密钥给第三方时，无法有效追踪到恶意的用户。文献［29］方案与文献［31］方案实现了可追踪可撤销的属性基加密方案，与本文方案相比，文献［29］方案与文献［31］的方案不支持外包解密。文献［32］方案虽然也实现了云雾计算下的可撤销属性基加密方案，但是不支持恶意用户追踪，且仅可以抵抗选择明文攻击。本文方案可以抵抗选择明文攻击和密钥伪造攻击。考虑到本文应用场景中，车辆作为一个边缘设备，并不具备强大的计算能力。因此，本文方案在保证数据机密性的前提下将部分解密计算外包给计算能力较强的雾节点，能够有效减轻车辆的计算开销。

表2 不同方案系统功能对比Tab.2 System function comparison of different schemes

表3 显示了本文方案与其他方案在性能方面的比较。方便起见，令E表示G、GT中的指数运算；P表示双线性配对操作；M表示G、GT中的乘法运算；l表示访问策略中属性的数目；r表示cover(R)的长度；s表示用户属性的数量；n表示解密密钥中满足访问策略的属性数。在密钥生成和加密算法中，本文方案的指数运算和乘法运算的复杂度比其他方案低，因此效率更高。在解密算法中，由于文献［22］方案、文献［29］方案和文献［31］方案不支持外包解密，所以用户解密的计算开销比本文方案要大得多，文献［30］方案的用户解密计算开销与本文方案持平，皆为一个指数运算与一个乘法运算，文献［32］方案的用户解密由一个配对运算与两个乘法运算组成，故本文的用户解密计算开销较小。与文献［22］方案、文献［29］方案和文献［31］方案相比，由于本文方案在跟踪方面具有更少的乘法运算与指数运算，因此本文方案在追踪方面的效率更高。

表3 不同方案系统效率对比Tab.3 System efficiency comparison of different schemes

6 结语

为了满足资源受限的边缘设备的数据访问需求，同时保证安全的数据共享，本文将云雾计算与密文策略属性基加密相结合，设计了一个安全的云雾设备数据共享方案，并实现了细粒度的访问控制。在本文方案中，车辆直接与本地雾节点进行通信，并将解密任务外包给雾节点执行，从而有效降低了用户的计算开销。由于雾节点只拥有外包解密密钥，因此无法获取明文，进而能够保证用户的隐私安全。本文方案还支持恶意用户的追踪与撤销，在解密密钥泄露的情况下，系统能够根据密钥追踪到用户的身份，进而将他加入撤销列表，使其失去数据访问权限。由于使用了直接撤销的方法，所以相较于间接撤销，本文方案能有效降低通信开销。此外，本文方案在选择明文攻击和密钥伪造攻击下被证明是安全的。由于本文的方案只能实现白盒可追踪性，不如黑盒可追踪性强。因此，我们的未来工作是构建具有黑盒可追踪性的基于密文策略的属性基加密方案。