基于万有引力的自适应近邻传播聚类算法

王治和，常筱卿，杜 辉

（西北师范大学计算机科学与工程学院，兰州 730070）

（*通信作者电子邮箱1478448005@qq.com）

0 引言

近邻传播（Affinity Propagation，AP）算法是一种新的聚类算法［1］，与K 均值聚类（K-means）和模糊C 均值（Fuzzy CMeans，FCM）相比，不需要确定最终的簇数。聚类中心是数据集中的现有数据点，而不是生成新的簇中心。该聚类算法的最大缺点是难以获得参数（偏向参数和阻尼系数）。

为了提高AP算法的聚类效果，许多学者对该算法进行了研究。文献［2］中提出的基于自适应属性加权的近邻传播聚类（Affinity Propagation clustering algorithm based on Adaptive Feature Weight，AFW_AP）算法利用聚类对象的聚类原理和聚类间对象的耦合原理自适应地改变属性权重，以更新相似度矩阵，吸引力和隶属度；文献［3］中提出基于同类约束的半监督近邻反射传播聚类方法（Semi-supervised Affinity Propagation clustering method with Homogeneity Constraints，HCSAP），引入了类似的约束项，改善了聚类目标函数；文献［4］中使用灰狼优化算法和二分查找算法分别自适应地调整偏置参数的上限、下限和中间值；文献［5］中使用极大团和势函数计算数据样本的概率密度，并使用该概率密度作为偏向参数；文献［6］中使用二分法动态更新偏差参数并选择有效性指标的最佳结果。上述文献研究得到了较好的聚类效果，但是存在以下两点不足：1）没有考虑AP 算法不适用于稀疏数据；2）在每次迭代中，正确聚类和错误聚类的样本将出现在同一簇内中，当更新属性权重时，为同一聚类中的样本赋予相同的权重，使同一个簇内的正确聚类和错误聚类的样本更加紧密，无法获得良好的聚类群集。鉴于这两点不足，本文提出了基于万有引力的自适应近邻传播聚类（Adaptive Affinity Propagation clustering based on universal Gravitation，GA-AP）算法。

GA-AP算法思想来源于对文献［7］的学习，发现万有引力搜索机制可以更好解决AP算法不适用于稀疏数据的问题；通过对文献［8-9］的学习，发现用分类算法可以很好地检测出数据集中的异常点。因此本文将信息熵［10］和分类算法AdaBoost［11］相结合，以检测每个簇内中正确聚类和错误聚类的样本点，并计算出样本点的权值。用该权值更新样本点从而重新调整相似度、Preference 取值、吸引度和隶属度，重新聚类。不断操作以上步骤直到达到最大迭代次数。实验结果表明，与其他聚类算法相比，GA-AP算法具有更好的聚类结果。

1 AP算法

AP 算法的基本思想是将所有数据点都视为潜在的聚类中心，其次将两对数据点之间连接起来以形成网络（相似性矩阵），最后在网络的每一端传递消息（吸引度和隶属度）以计算每个样本的聚类中心［12］。

现有X={x1，x2，…，xn}，X是n×d的矩阵，n是样本数，d是维数。相关概念［13］如下：

1）相似度矩阵（Similarity matrix，S）：计算n个点之间的相似度（欧氏距离的负值），这些相似度形成一个相似度矩阵。

2）偏向参数（Preference）：聚类中心的参考度（不能为0），通常设置为S相似度值的中位数，该值越大，聚类中心越多的可能性越大。

3）吸引度矩阵（Responsibility，R）：点xk适合作为数据点xi的聚类中心的程度表示为R(xk，xi)。

4）隶属度矩阵（Availability，A）：点xi选择点xk作为其聚类中心的适合程度，记为A(xi，xk)。

5）阻尼因子（λ）：主要是起收敛作用的。

传统AP算法的流程，如图1所示。

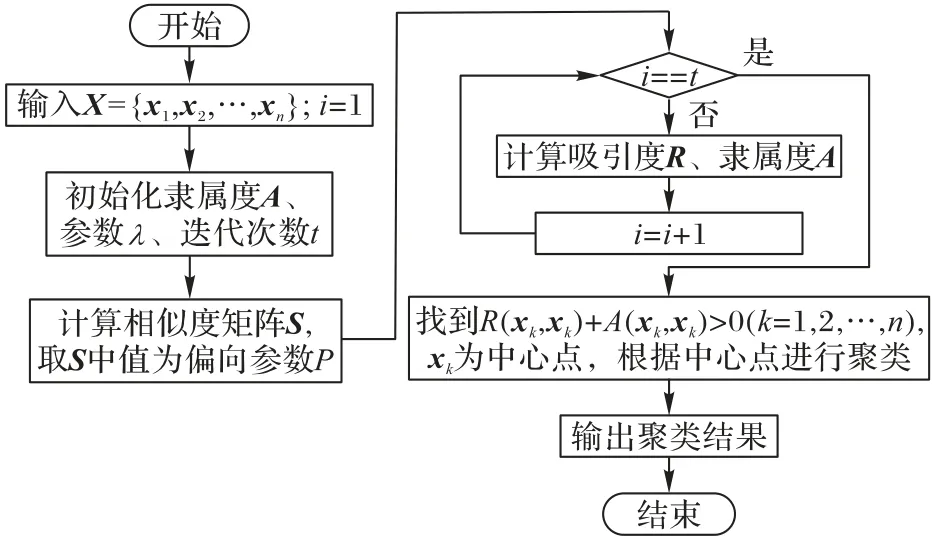
图1 AP算法流程Fig.1 Flowchart of AP algorithm

2 万有引力的自适应近邻传播聚类算法

2.1 算法思想

传统AP聚类算法的聚类结果受参数Preference 的影响很大、不适用于稀疏数据且该算法得到的类簇内会出现错误划分的样本点。为了解决这些问题，本文提出新的AP聚类算法——GA-AP算法。GA-AP算法与传统AP算法的区别：1）传统AP 算法容易使得稀疏数据陷入局部一致性，因此AP 算法不适用于稀疏数据；GA-AP 算法借助万有引力搜索机制对样本进行全局寻优；2）传统AP算法中的Preference参数为固定值，以及传统AP聚类算法得到的簇内会出现错分的样本点，从而使得聚类结果很差。GA-AP算法首先利用信息熵和AdaBoost计算前一次迭代时每个簇内正确聚类的样本权重和错误聚类的样本权重；其次用得到的样本权值更新样本特征，从而动态调整下一次迭代的相似度和偏向参数Preference，以减少簇内错分点和自适应调整参数。

2.2 欧氏距离的局部性

传统AP算法通常用欧氏距离来衡量对象间的相似度，但是欧氏距离表示的是空间上相邻的数据点之间具有较高的相似性，因此，使用欧氏距离度量AP算法的相似度矩阵，很难使稀疏数据达到全局一致性，进而严重影响聚类性能。

为了进一步的说明该问题，本文用Compound数据对其进行分析，如图2所示。

图2 欧氏距离无法显示稀疏数据的全局一致性Fig.2 Euclidean distance cannot showing the global consistency of sparse data

由图2 可以直观看出：数据点1 与数据点2 的相似性要比数据点1与数据点3的大。但是，如果按欧氏距离作为相似度测量，则数据点1 与数据点3 的直线距离很明显小于数据点1与数据点2 的距离，这样数据点1 与数据点3 划分为同一类的概率将大于数据点1与数据点2。即：用欧氏距离作为数据点相似度测量时无法反映图2 所示的全局一致性。因此，对于稀疏数据集，AP算法简单用欧氏距离计算数据点之间相似性会严重影响聚类算法的性能。

2.3 基于万有引力的AP算法

为了解决传统AP 算法使稀疏数据达不到全局一致性的问题，本文用万有引力搜索机制对传统AP算法改进。

万有引力定律［14-15］公式如式（1）所示：

其中：M1、M2是物体的质量；G是常量6.67*10-11N·m²/kg²，r是物体间的距离。

万有引力通过物体的质量与距离反映物体间的吸引力，质量越大，距离越近的物体吸引力越强，这与聚类分析中衡量对象间的相似度类似。

基于万有引力的AP 算法是采用万有引力搜索机制对样本进行全局搜索，以此衡量对象间的相似度，并将此用于AP算法提高聚类效果。

基于万有引力的AP算法原理：通过样本间的相互引力的作用进行优化搜索，每个样本受到空间中其他样本的引力的影响，产生加速度向特征相近的个体靠近。样本集中的具有不同特征的样本，通过万有引力在解空间中相互吸引，样本的引力由其特征和样本间距离决定。样本在引力的作用下向其特征和距离相近的其他样本靠近，即逐渐逼近优化问题的最优解。具体形式如下：

假设给定现有X={x1，x2，…，xn}，计算数据集X的相似度公式如下：

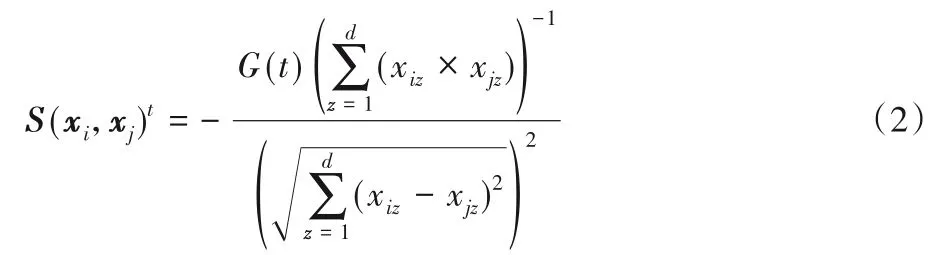
其中：t是迭代次数对象间特征乘积之和的倒数，这里之所以取倒数是因为对象特征不同于物体的质量。现实中两个物体的质量越大引力越强，但是对于两个样本的特征却相反（一个样本的特征与其他的样本特征越相近则该样本对其他样本的吸引力越强，其他样本均向其靠近）；是距离度量，取值为对象间欧氏距离的2 次方；G(t)为第t次迭代的万有引力系数，该系数随着迭代次数的增大而动态地减小，能更好地控制搜索过程：

其中：tmax为最大迭代次数，G0和a为常量。G(t)的取值能更好地平衡算法的全局搜索能力和局部搜索能力。

为了进一步说明该原理，对其进行详细分析，如图3所示。

图3 基于万有引力的相似度Fig.3 Similarity based on universal gravitation

从图3中看出：样本点1和3为同一类，与样本2、4是不同类的。样本点1 和3 特征相似，与样本点2、4 特征不相似；样本点1 和3 距离最远，与样本点2、4 距离近。如果用欧氏距离测量相似度，则样本点1和3归属于一类的概率远小于与样本点2、4 归属于一类的概率。用万有引力测量相似度，则发现样本点1 和3 的引力远大于与样本点2、4 的引力，这说明样本点1和3归属于一类的概率远大于与样本点2和4归属于一类的概率。因此在AP算法中用万有引力测量相似度，可以解决传统AP算法使稀疏数据达不到全局一致性的问题。

算法2 基于万有引力的AP 算法，给定数据集X={x1，x2，…，xn}。

步骤1 算法初始：归属度初始化为0，输入参数λ和最大迭代次数t。

步骤2 式（2）计算相似度矩阵S(xi，xj)，将相似度矩阵的中值赋值给Preference。

步骤3 用式（5）和式（8）分别更新吸引度矩阵R和归属度矩阵A。

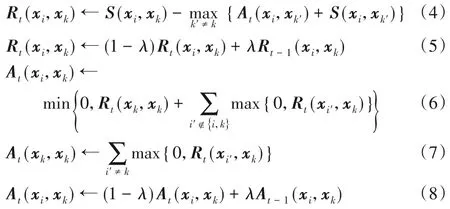
步骤4R(xk，xk)+A(xk，xk)＞0(k=1，2，…，N)时，xk是聚类中心，并将各数据分配到离其最近的中心点中。

2.4 参数Preference取值

为了降低参数Preference 取值对AP算法聚类效果的影响以及减少簇内错分的样本点，本文利用信息熵和自适应增强算法（AdaBoost）对该算法进行优化。

基于自适应增强算法的AP 是用信息熵和AdaBoost 算法计算出前一次迭代的每个簇内错误聚类和正确聚类的样本点，并得到这些样本点权值，用该权值更新样本特征，从而为下次迭代重新获取合适的Preference参数值。具体形式如下：

假设给定数据集X={x1，x2，…，xn}，其中xi={xi1，xi2，…，xid}∈X；类别集C={c1，c2，…，cK}，其中ci={x1′，x2′，…，xi′′}∈X，K是类别数；聚类中心集Q={q1，q2，…，qK}，其 中qi={qi1，qi2，…，qid}；数据集权值W={w1，w2，…，wn}。

算法3算法流程如下：

步骤2 进行迭代t=1，2，…，T。

1）计算每个簇内的每个样本的信息熵，如：

2）找到每个簇内错误的聚类样本点（簇内最大的样本点信息熵）xu′和xu′所对应的类权值wi，计算其误差率et：

3）计算每个簇内的每个样本权值。

正确聚类样本点的权值（用除x′u以外样本点的权值分别除以2 ×(1-et)：

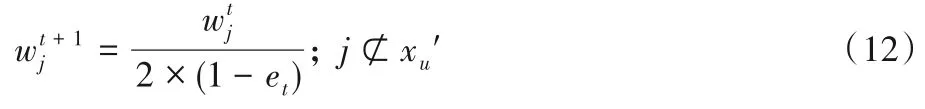
错误聚类样本点（xu′）的权值：

步骤3 用得到的样本点权值更新数据集。

步骤4 重新计算相似度矩阵、Preference值，重新聚类。

2.5 GA-AP的算法步骤

为了解决AP 不适用于稀疏数据的问题、降低参数Preference 值对算法的影响以及减少簇内错分的样本点，本文提出了GA-AP 算法。该算法在传统的AP 算法的基础上采用引力搜索机制对样本全局寻优，有效解决了AP不适用于稀疏数据的问题，并且在此基础上用信息熵与AdaBoost 算法自适应地调整参数Preference 以及减少簇内错分点，提高AP 算法的聚类效果。GA-AP算法流程如图4。

图4 GA-AP算法流程Fig.4 Flowchart of GA-AP algorithm

3 实验结果与分析

3.1 实验环境

实验环境为Windows7 64 位操作系统，Intel Core i7 2.7 GHz CPU，16 GB 内存，使用Matlab2016a 软件进行实验。本文做了5 次实验，取评价指标的均值来评估算法的聚类效果。算法中的迭代次数t设置为50，阻尼因子λ为0.8，G0取值为100，a取值为20。

3.2 Preference参数的变化

Preference 参数对AP 算法有着很大的影响，Preference 值越大，则算法得到的聚类结果越好。传统AP 算法的Preference 参数为固定值，而GA-AP 算法的Preference 值会随着每次的聚类结果进行调整以达到一个优越的值。图5 显示GA-AP 算法在运行Iris、Seeds-dataset、Wine、Haberman 四组数据时，每次迭代Preference 的变化。可以看出这四组数据的Preference 值随着迭代次数的增长而不断地增大。Iris、Wine两组数据在第30 次迭代时，Preference 取值基本达到稳定；Seeds-dataset、Haberman两组数据在第40次迭代时，Preference 取值基本达到稳定。这四组数据的Preference 取值在第50次迭代时基本趋近于-1。

图5 偏向参数值的变化Fig.5 Change of Preference

3.3 对稀疏数据的比较

GA-AP 算法克服了AP 算法不适用于稀疏数据这一不足之处。为了验证其效果，本文选取三组数据（Threecircles、Lineblobs、Compound）在GA-AP 算法、AP 算法、K-means 算法和FCM 算法上运行，判断GA-AP 算法是否有效地克服这一不足。效果图为图6。

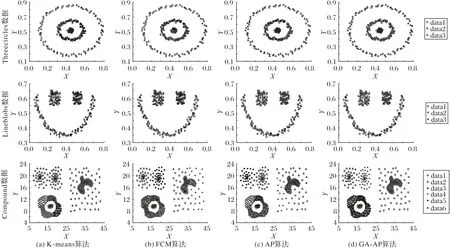
图6 四种算法对稀疏数据的聚类结果Fig.6 Clustering results of four algorithms on sparse data

综合图6 明显看出在Threecircles、Lineblobs 和Compound三组数据上，GA-AP 算法相对于AP 算法、K-means 算法和FCM 算法在处理稀疏数据时可以得到很好的聚类效果，因此GA-AP算法能更好地平衡全局搜索能力和局部搜索能力。

3.4 与其他聚类算法性能对比

在本节中，将通过UCI 和人工数据集对GA-AP 算法进行验证，使用以下的数据集：UCI 数据、人工数据（Threecircles、Lineblobs）。为了更好地评估该算法的聚类性能，本文用纯度（Purity）、F-measure［16-17］和准确性（ACC）［18］三种评价指标比较GA-AP 算法与AFW_AP 算法、AP 算法、K-means 算法和FCM算法的聚类结果。

表1 介绍了9 个数据集的特征，分别是数据数目、特征值和类别数。

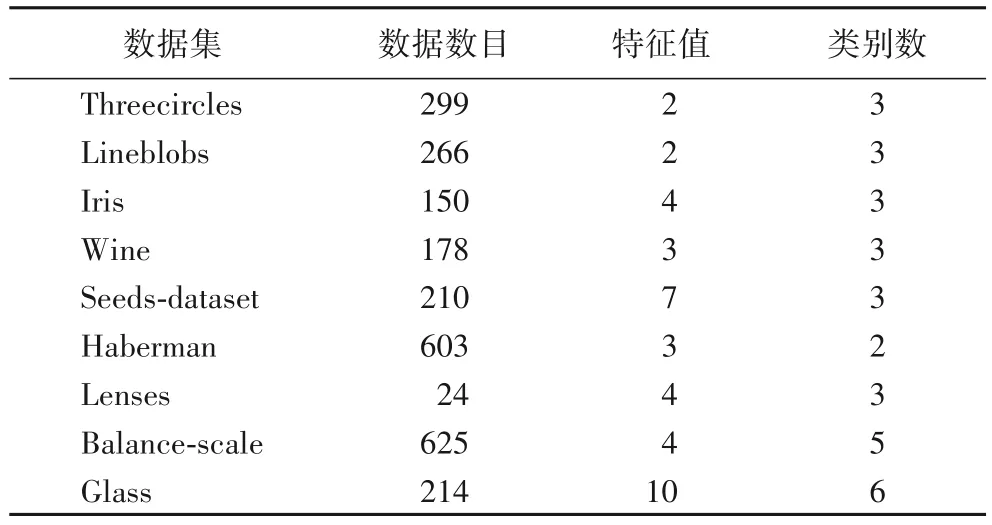
表1 数据集的基本信息Tab.1 Basic information of datasets

为了更好地验证GA-AP 算法的聚类效果，本文将该算法与AFW_AP 算法、AP 算法、K-means 算法和FCM 算法的聚类效果进行对比，如表2（准确率评价表）、图7（F-measure 评价图）和图8（纯度（Purity）评价图）。

图7 五种算法聚类效果F-measure评价Fig.7 F-measure evaluation of clustering effect of five algorithms

图8 五种算法聚类效果Purity评价Fig.8 Purity evaluation of clustering effect of five algorithms

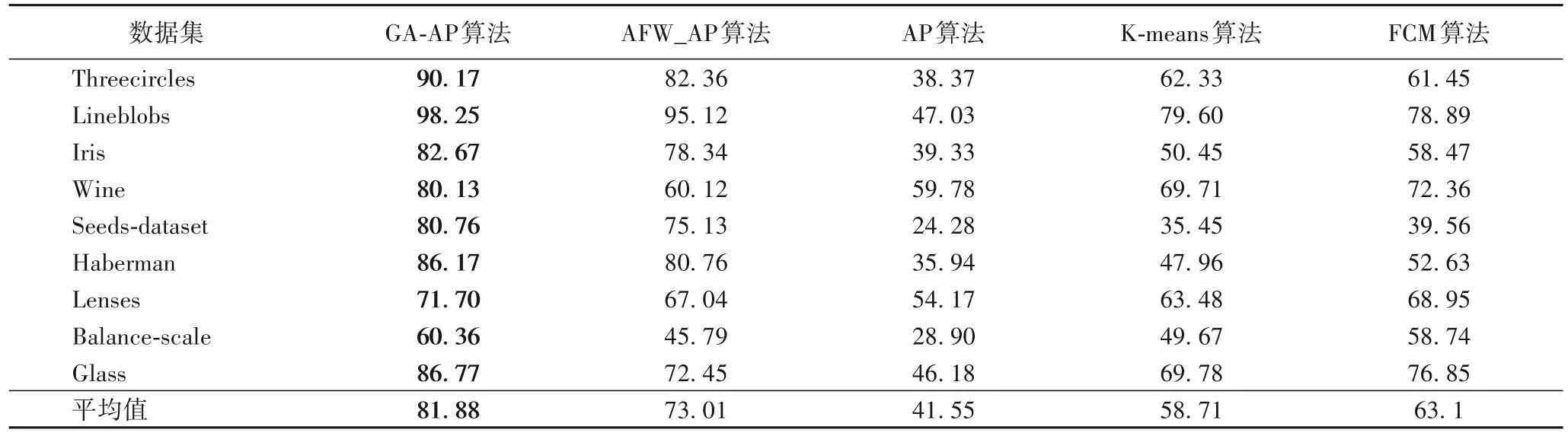
表2 五种算法聚类效果准确率评价表 单位：%Tab.2 Accuracy evaluation table for clustering effect of five algorithms unit：%

从表2 可以分析出，GA-AP 算法针对Threecircles、Lineblobs、Iris、Seeds-dataset、Wine、Haberman、Lenses、Balancescale 和Glass 这9 组数据集的聚类结果的准确率高于AFW_AP 算法、AP 算法、K-means 算法和FCM 算法，这说明GA-AP 算法提高聚类正确的样本数，且其对于稀疏数据有更好的处理。如在Threecircles 数据集上，GA-AP 算法得到的ACC 为90.17%；AFW_AP 算法、AP算法、K-means算法和FCM算 法 得 到 的ACC 分 别 为82.36%、38.37%、62.33% 和61.45%。在Seeds-dataset 数据集上，GA-AP 算法得到的ACC为80.76%；AFW_AP 算法、AP 算法、K-means 算法和FCM 算法得到的ACC分别为75.13%、24.28%、35.45%和39.56%。

由图7 可以分析出，GA-AP 算法针对Threecircles、Lineblobs、Iris、Seeds-dataset、Wine、Haberman、Lenses、Balancescale 和Glass这9组数据集的聚类结果的F-measure高于AFW_AP算法、AP算法、K-means算法和FCM算法。如在Threecircles 数据集上，GA-AP 算法得到的F-measure 为100%；AFW_AP算法、AP算法、K-means算法和FCM算法得到的F-measure 分别为59.19%、32.7%、46.38% 和49.35%。在Lenses数据集上，GA-AP算法得到的F-measure为80%；AFW_AP算法、AP算法、K-means算法和FCM算法得到的F-measure 分别为67.04%、39.80%、42.36%和45.23%。

由图8 可以分析出，GA-AP 算法针对表1 中这9 组数据集的聚类结果的纯度高于AFW_AP 算法和AP 算法，这说明GAAP算法得到的簇内样本数与真实标签的簇内样本数很接近。如在Lineblobs 数据集上，GA-AP 算法得到的Purity 为0.91；AFW_AP算法、AP算法、K-means算法和FCM算法得到的Purity 分别为0.87、0.22、0.25 和0.3。在Balance-scale 数据集上，GA-AP 算法得到的Purity 为0.52；AFW_AP 算法、AP 算法、K-means 算法和FCM 算法得到的Purity 分别为0.34、0.25、0.35和0.36。

结合上述实验，从Purity、F-measure 和准确率这三个评估指标的测量结果分析出：GA-AP 算法相比于AFW_AP 算法、AP 算法、K-means 算法和FCM 算法，GA-AP 算法得到的簇内样本点与真实标签的簇内样本点更接近。

4 结语

对于AP 算法不适用于稀疏数据、对Preference 参数敏感以及簇内会出现错分点的问题，本文提出基于万有引力的自适应AP 算法（GA-AP 算法）。实验结果表明，与AFW_AP 算法、AP 算法、K-means 算法和FCM 算法相比，GA-AP 算法的聚类结果更接近真实类别标签。后续研究将关注如何加快GAAP算法的运行，进一步提高该算法的运行效率。