初中尺规作图教学谈
郑艳 石树伟

摘要:由一道限定工具作图题反思初中尺规作图教学的现状、价值与方法。尺规作图作法的生成过程是应用几何原理解决新问题的过程,也是执果索因思考的过程,可以培养学生的逻辑推理能力、探索性思维以及应用意识和创新意识。因此,尺规作图教学不应该局限于技能的传授,而应该让学生充分经历作法的生成过程。
关键词:限定工具作图;尺规作图;作图道理;作一个角的平分线
一、九年级学业质量监测中的一道限定工具作图题
近日,一次九年级学业质量监测中有这样一道限定工具作图题:
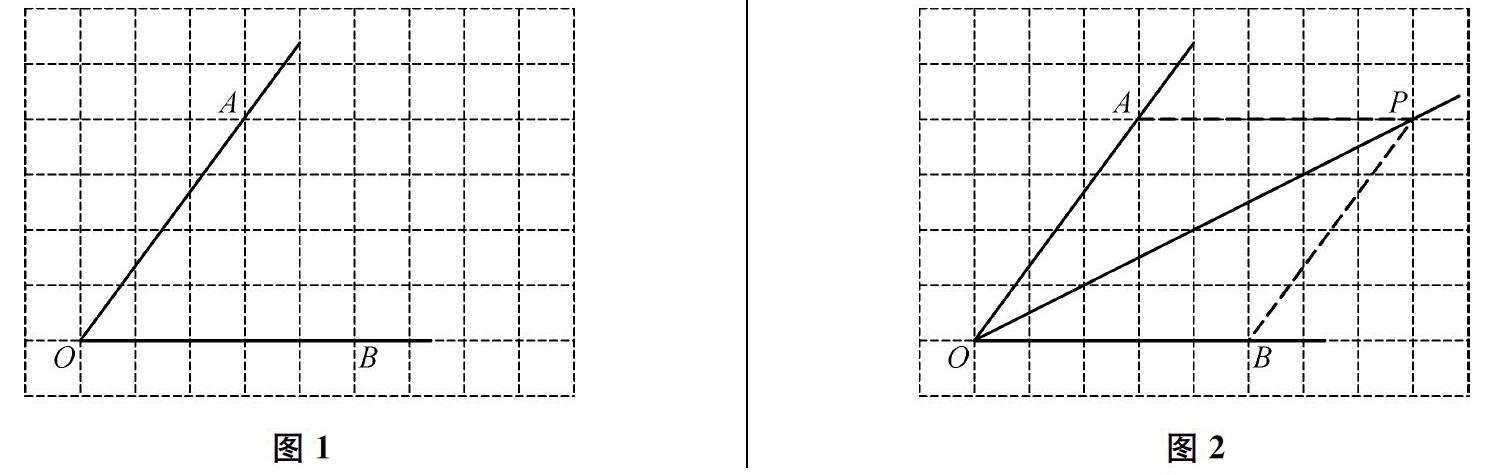
如图1,∠AOB放置在正方形网格中,点A、O、B在格点上。请你仅用无刻度的直尺画出∠AOB的角平分线,保留画图痕迹并说明理由。
解决本题的思路分析如下:
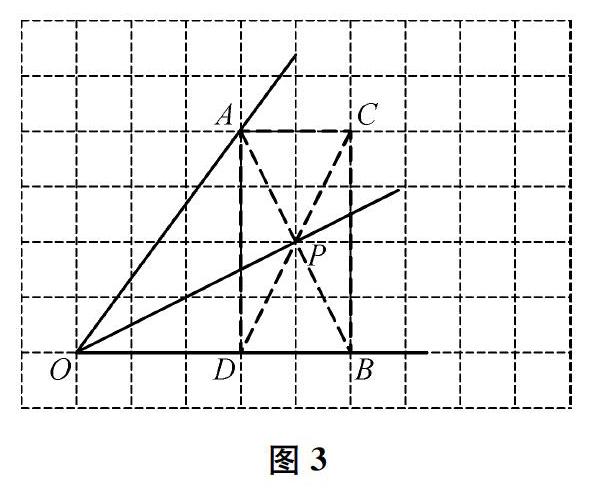
仅用无刻度的直尺画∠AOB的角平分线,需充分借助网格并利用相关几何性质。初中几何与平分角相关的性质主要有 “菱形对角线平分一组对角”和“等腰三角形三线合一”。因此,可以借助网格构造菱形(如图2)或等腰三角形(如下页图3)解决本题。
考试中本题的答题情况很不理想。考试后有学生反映:仅有直尺没有圆规,而直尺无刻度只能用来连线,不知道从哪里画起;虽然学过尺规作图,但只需按指定步骤操作,不需要想怎么作,从没有遇到过这类问题,不知道从哪里想起。
其实,尺规作图也属于限定工具作图。由此,引发笔者对当前初中尺规作图教学的反思。
二、对尺规作图教学的反思
《义务教育数学课程标准(2011年版)》规定的初中尺规作图内容,主要包括四个方面:一是利用尺规完成一些基本作图(包括作一条线段等于已知线段,作一个角等于已知角,作一个角的平分线,作一条线段的垂直平分线,过一点作已知直线的垂线);二是利用基本作图作三角形(具体内容省略);三是利用基本作图完成一些与圆相关的作图(具体内容省略);四是“在尺规作图中,了解作图的道理,保留作图的痕迹,不要求写出作法”。其与之前的教学大纲和课程标准(实验稿)相比,最大的变化是要求学生了解作图的道理(比如,作一个角等于已知角、作一个角的平分线、作一条线段的垂直平分线、过一点作已知直线的垂线等基本作图的原理就是三角形全等)。
但是,现行教材仅提供了规范的作法和保留痕迹的作图示范,教师的教学受到习惯的影响,仅教给学生作法,将尺规作图当技能来训练——尤其是对利用尺规完成一些基本作图而言。调查发现,现在大部分学生没有想过为什么这样作图,更不用说知道怎么想到这样作的。在许多学生心目中,尺规作图只需按步骤操作,尺规作图是“不讲道理的数学”。也就是说,“了解作图的道理”这一课标教学要求没有完全落实到位。
(一)信息时代尺规作图的教学价值
张奠宙先生指出,数学“双基”要与时俱进。过去,工程绘图、工艺设计、教师教学、学生学习要绘制精准图形,必须用尺规作图,因此,尺规作图是学生未来继续学习和参加工作必备的基本技能。现在,信息技术飞速发展,各种绘图软件易学又好用,日常科研、生产、教学中的手工绘图已经基本上被计算机所替代,可以说,尺规作图已经不再是现代学生的必备技能。
那么,尺规作图的教学价值又在哪里呢?就在“了解作图的道理”中。尺规作图教学不仅要让学生在作图之后知道为什么这样作,而且要让学生在作图之前知道怎么想到这样作。尺规作图作法的生成过程,是应用几何原理解决新问题的过程,也是执果索因思考的过程,可以培养学生的逻辑推理能力、探索性思维以及应用意识和创新意识。
尺规作图教学中,经历作法的生成过程对学生应用几何原理解决其他作图问题有较大的帮助,可以为学生提供作法分析策略的宏观指导和作法分析过程的具体示范。例如,对于文章开头提到的限定工具作图题,学生首先要想哪些几何结论可以得到角平分线或角相等,然后要分析哪个结论能用来在网格中仅用无刻度的直尺作出角平分线:用菱形对角线平分一组对角需考虑在网格中能否仅用直尺构造菱形,用等腰三角形“三线合一”需考虑在网格中能否仅用直尺构造等腰三角形及其底边中点。如果在尺规作图教学中学生经历了作法的生成过程,那么在解决限定工具作图问题时学生会有意识地按照上述思路进行分析。
其实,运用信息技术作图本质上也是限定工具作图,其限定的工具就是作图软件。有时,为了精准作图也需要充分利用几何原理构造图形。例如,“正多边形与圆”一节教学,教师在前期教学中已经指导学生掌握了几何画板软件的基本操作,学生已经能够在电脑上独立使用几何画板软件。课上,教师先让学生运用几何画板软件绘制正三角形、正方形、正六邊形,然后有选择地请部分学生通过几何画板软件的“显示/隐藏”功能展示自己的作图方法,介绍自己的作图思路及依据。学生的作图方法可以分为两种:(1)通过线段的摆放画出正多边形,这种作法形“似”神散,随意拖动正多边形的任一顶点,图形便会“散架”;(2)通过几何关系构造正多边形(常见构造方法见图4),这种作法形“是”神聚,随意拖动正多边形的任一顶点,图形只会改变位置和大小,不会改变几何关系。后一种画法才是学生需要掌握的画法。这种画法需要根据正多边形各边相等、各角也相等的本质特征,充分利用圆的几何性质构造图形,其思考分析方法和能力素养要求与限定工具作图(包括尺规作图)是一致的。
(二)信息时代尺规作图的教学方法
信息时代尺规作图教学不应该局限于技能的传授,而应该提升教学立意,让学生充分经历作法的生成过程:操作前要引导学生思考分析如何作图,感悟“是怎么想到这样作的”;操作后要追问这样作的道理,知道“为什么这样作”。以“尺规作图——作一个角的平分线”为例,教学设计如下:
问题1尺规作图就是只用无刻度的直尺和圆规作图。无刻度的直尺和圆规分别可以用来做哪些事?
教师引导学生回忆、思考、讨论,形成“无刻度的直尺可以用来连线,圆规可以用来画圆弧,进而可以截取等长线段”的认识。
问题2造房子一般先要有图纸,然后根据图纸去想怎么造。画图也一样,先要有“圖纸”。假设已经画成功了,“效果图”如图5所示,其中∠AOM=∠BOM。我们学过哪些原理可以得到角相等?如何构造使用上述原理得到角相等所需要的图形(“施工图”)呢?
学生容易想到“全等三角形对应角相等”。教师通过追问启发学生思考如何构造一对全等三角形使得∠AOM=∠BOM,形成如图6所示的“施工图”,其中OC=OD,CP=DP。然后引导学生发现,利用尺规能够实现OC=OD,CP=DP。
问题3根据“施工图”(图6),该如何用尺规操作?请尝试操作。
教师引导学生自己说出尺规作图作一个角的平分线的基本步骤,并让学生动手操作。
问题4根据刚才尺规作图的操作过程,你能说明OM平分∠AOB的道理吗?
教师引导学生根据操作过程提取作图满足的条件,然后说明OM平分∠AOB的道理。
上述教学设计中,问题1让学生明晰“我已有什么”,即现有的作图工具及其功能;问题2通过“效果图”,让学生明晰“我要做什么”,并引导学生逆向分析得到“施工图”,即知道“我怎么做到”;问题3引导学生经历作图的过程;问题4引导学生由操作过程反思理解作图的道理。
问题3、问题4就是我们常说的不仅让学生“知其然”,还能“知其所以然”;问题1、问题2则进一步引导学生不仅经历作法的形成过程,自己发现作法,而且从“知其然”“知其所以然”上升至知“何由以知其所以然”。这样的设计,充分发挥了尺规作图的教学价值。
此外,尺规作图教学还要尽量避免这种情况:作法是学生发现的,却是在教师各种缺乏思维含量的提示和铺垫下“发现”的。这样的“发现”不是真发现。
例如,“尺规作图——作一个角的平分线”的教学中,有的教师为了让学生自己“发现”尺规作角平分线的方法,给出了如下的问题:
工人师傅常常利用角尺平分一个角。如图7,在∠AOB的两边OA、OB上分别任取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,则过角尺顶点M的射线OM就是∠AOB的平分线。请你说明这样来画角平分线的道理。从木工师傅的画法中,你能找到用直尺和圆规作角平分线的方法吗?
通过对这个前置问题的思考,学生容易得到尺规作角平分线的方法,但是,这样的发现是“假发现”。因为问题给出的画法与尺规作法太接近,导致从前者到后者的过程缺少思维含量。而且,前置的问题就如同“天上掉下的馅饼”,学生以后遇到新的作图问题时是想不到的。
*本文系江苏省扬州市教育科学“十三五”规划2016年度立项重点课题“‘重塑本色追求本质数学教学主张的理论与实践研究”(编号:G/16/Z/006)的阶段性研究成果。
参考文献:
[1] 张奠宙,赵小平.“与时俱进”话“双基”[J].数学教学,2001(5).
[2] 石树伟.借助技术操作体验:数学史融入数学教学的新尝试——以“正多边形与圆”的教学为例[J].数学通报,2018(12).

