基于记忆多项式模型的选择自适应预失真系统

易胜宏，张红升，孟 金，马小东

（重庆邮电大学 光电工程学院，重庆400065）

功率放大器（power amplifier，PA）是无线通信系统中的重要模块，其性能特点备受学者们的研究，其中比较热门的研究方向是功率放大器的线性化技术，即预失真技术（pre-distortion，PD）。由香农定律可知，要提高数据传输速率，势必要提高数据传输带宽，为了提高频谱利用率，当今对于数字基带信号的调制方式几乎都是高阶调制方式，比如8PSK，16QAM，64QAM，OFDM 等。这些调制方式都是非恒定包络的，并且其调制载波数量高达几十个甚至上千个，因此在调制之后会产生较高的均峰比[1]（peak to average power ratio，PAPR）。高PAPR 信号通过功放时，由于功放器件的记忆性和非线性特性，其输出信号幅度曲线将产生比低PAPR 信号更严重的非线性畸变[2]，信号频谱将展宽至自身频带宽度的3倍及以上，严重影响相邻频带的传输效率。

解决这种非线性失真的方法包括功率回退法、模拟预失真法和数字预失真法等，其中，数字预失真法（digital pre-distortion，DPD）由于其灵活性和低成本性，已被广泛地应用在工程设计中。目前，常用的数字预失真结构包括直接型与间接型[3]，直接型结构的收敛速度较快，但收敛后的信号较原始信号的误差较大；间接型结构的收敛误差较小，但收敛速度较慢，且容易引入噪声干扰预失真效果。针对上述结构的不足，本文采用记忆多项式（memory polynomial，MP）模型，提出新型选择预失真结构。通过Matlab 仿真，本文所提出的选择预失真结构系统在提高系统收敛速度的同时，降低了系统的收敛误差。

1 数字预失真的基本原理

功率放大器的非线性失真是电子元器件的物理特性所导致的，非线性失真即功放的输出信号相对于输入信号产生的非线性形变。通常情况下，可以通过降低输入功率来保持输入输出功率的线性关系，但这会大大降低功放的效率[4]。数字预失真的原理是，预先将输入信号进行畸变处理，即数字信号处理，使得畸变后的信号通过功放时，与功放所造成的畸变相补偿，使得输入-输出信号整体呈现出线性的品质。数字预失真的原理如图1所示。

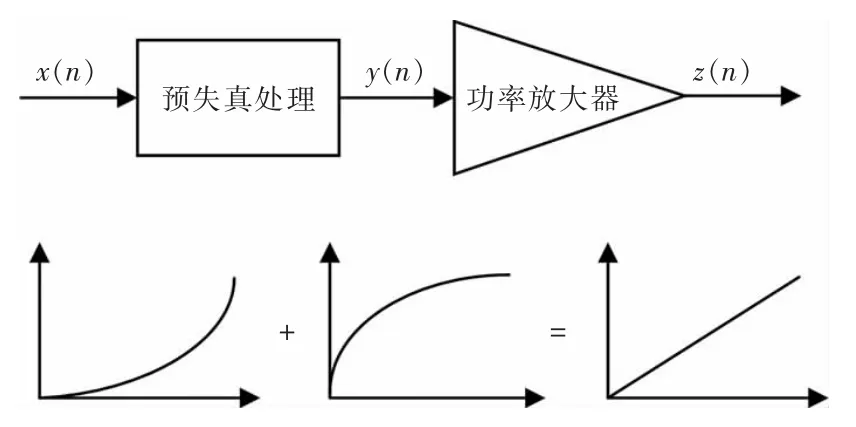
图1 数字预失真原理图Fig.1 Principle of DPD

图中，x（n）为预失真器输入信号；y（n）为经过预失真处理后的输出信号；z（n）为功放输出信号。

式中：h（x）为功放的传输函数，预失真器的传输函数和功放的传输函数互为反函数，记为h-1（x），所以预失真器的输出可以表示为

将公式（2）代入公式（1）中，得到公式（3）为

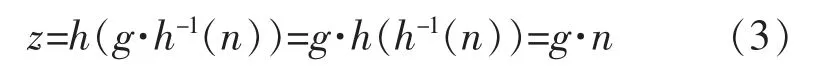
式中：g为常量，表示的是功放的增益因子，可以看出，经过预失真器后，功放的输出信号相对于输入信号是整体线性放大的。

2 新型数字预失真结构

2.1 现有结构

目前，数字预失真系统的结构包括直接型与间接型，直接预失真模型的原理如图2所示。

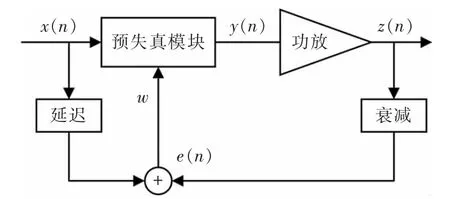
图2 直接型预失真结构原理图Fig.2 Schematic diagram of direct structure

此模型的基本思想是将代价函数定义为衰减后的功放输出信号与输入信号之间的误差，通过自适应算法模块不断迭代，替换模型系数，更新预失真器的参数，使得衰减后的输出信号与输入信号之间的误差（代价函数）值最小化。在理想情况下，预失真处理和功放的行为是互逆的两个过程，但此结构存在不稳定性，如果均方误差（mean square error，MSE）不是关于功放拟模型参数的二次函数，容易造成局部收敛的情况，导致系统的局部收敛情况[5]。其中x（n）为预失真器的输入信号；y（n）为功率放大器的输出信号；e（n）为x（n）与y（n）经过衰减后的误差信号。

间接型预失真模型的原理如图3所示。间接预失真结构是一种开环式的预失真结构，计算功放输入与训练模块输出之间的误差，其中z1（n）为功放输出经过自适应算法训练后的输出，使得预失真模块的输出信号向自适应算法输出信号逼近。间接预失真模型的优点是不需要提前了解功率放大器的非线性特点和估算非线性函数，即可准确和稳定的建立预失真模型，能稳定得到系统全局的最优解；缺点是由于间接预失真结构求取的是功放的后置逆，功放输出反馈回来的信号经过下变频和AD 转换后会引入噪声，其预失真后的输出信号线性度较差[6]，模型参数会产生一定程度的偏移。

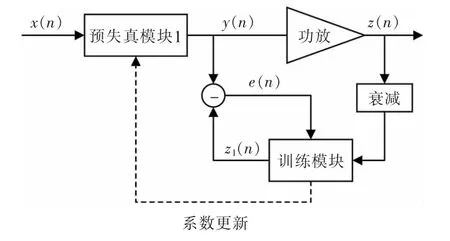
图3 间接型预失真结构原理图Fig.3 Schematic diagram of indirect structure

2.2 改进结构

根据两种结构的优缺点，本文提出一种闭环的选择预失真结构，其原理如图4所示。

图4 选择预失真结构原理图Fig.4 Schematic diagram of selective structure

图中：x（n），y（n），z（n）分别为系统输入信号、主预失真模块输出信号、系统输出信号；PA 为功率放大器；z1（n）为系统输出衰减后的信号；e1（n）为系统输入信号经过延迟后与z1（n）的误差信号；e2（n）为主预失真器的输出信号与z1（n）经过副预失真器处理后的输出信号的误差信号。比较器计算e1（n）与e2（n）的幅度大小，并与零值相比较，更靠近零值的误差信号所对应的自适应模块输出会通过二选一选择器输出，作为主预失真器的复增益系数w（n+1），来替代自适应模块1 的迭代复增益系数w1（n+1），其中，w2（n+1）为自适应模块2 的迭代复增益系数。

2.3 数学分析

预失真系统的输入信号为x（n），根据3 条路线的处理途径，可以得出e1（n）和e2（n）的公式为

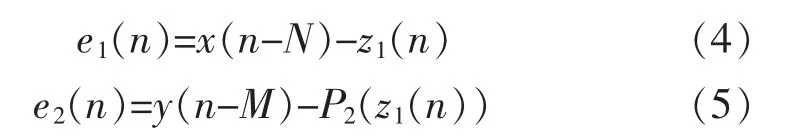
式中：P2（.）为预失真模块2 的非线性基函数；N为结构1 延迟的采样点数；M为结构2 延迟的采样点数，对于y（n）与z（n），有：

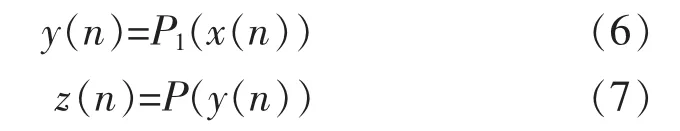
式中：P1（.）为预失真模块1 的非线性基函数；P（.）为功率放大器的非线性基函数。

输入延迟信号与输出信号的误差信号通过NLMS 算法实现对主预失真模块的参数调整，由于结构1 的模块较少，结构简单，延迟较小，故收敛速度较快，但对于非线性特性很强的功率放大器，误差信号较大，故收敛后的NMSE 也较大[7]。其迭代公式为

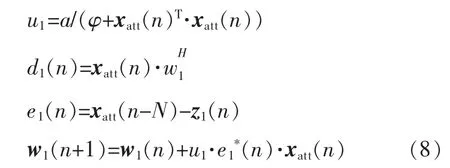
其中：a为一个固定的收敛因子，使算法收敛的a值范围为0＜a＜2；φ 是一个很小的常数，一般取0；d1（n）为xatt（n）经过抽头系数为w1的FIR 滤波器后的输出信号；xatt（n）为输出衰减后的反馈信号；x（n-N）为输入信号的延迟，其中N为延迟项数；u为可变步长因子；w1为主预失真模块的模型系数，可以表示为

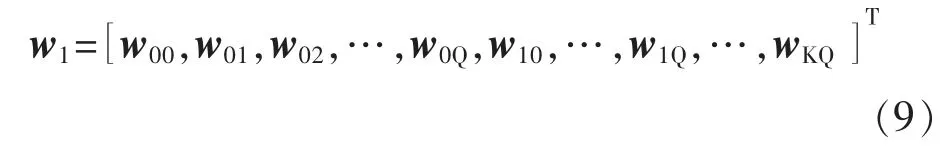
式中：Q为预失真模型的记忆深度；K为其非线性阶数。同理，将式（5）中的预失真模块2 的输出带入至自适应算法中，则结构2 的自适应算法表达式为

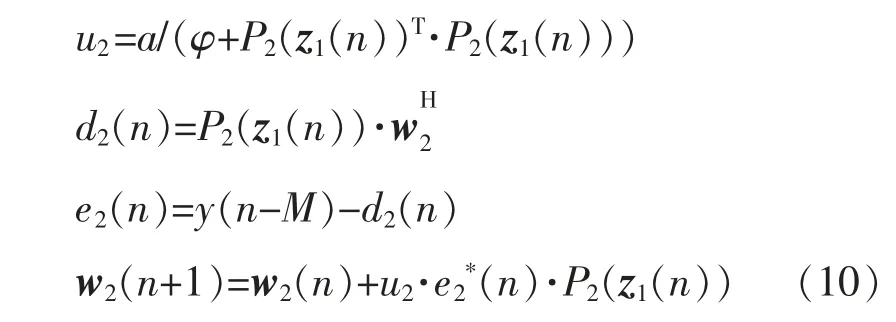
在系统收敛后，e1（n）≈e2（n）≈0，主预失真模块与副预失真模块均为功率放大器的逆模型，即：

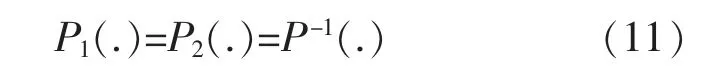
根据结构2 的特性，其数据流动的模块较多，故收敛速度较慢，但根据后续仿真的结果可以看出，其结构的收敛后的误差信号相较于结构1 减小了0.5 个数量级。通过结合结构1 与结构2 能更好地实现数字预失真系统的收敛，通过1 个比较器与1 个选择器就能实现该结构。

2.4 模型选择

Volterra 级数是由意大利数学家Vito Volterra的泛函理论演变而来的，它被称为“有记忆效应的泰勒级数”，是因为它包含了具有自变量的高次项和延迟项，这两种特点使得此级数与功放的非线性和记忆性等物理特性不谋而合[8]，Volterra 级数的表达式为

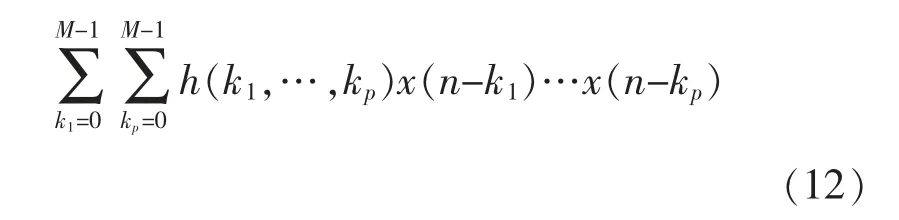
式中：y（n）与x（n）分别为通信系统的输出信号与输入信号；M为模型的记忆深度；P为非线性阶数；kp为对应的记忆项系数。Volterra 模型包含延迟项和高次项，表现出功放特有的记忆性和非线性，能够对输入信号的记忆非线性的特征描述得十分准确。但是，考虑到记忆深度为3，非线性阶数为5 时，整个模型的系数个数已经高达526 个，可以看出，Volterra 级数的模型系数随着记忆深度和非线性阶数的增加而急剧增加，复杂度过高。

本文的主预失真模块与副预失真模块均采用记忆多项式模型，数学表达式为

记忆多项式模型由于其较少的模型参数与延迟项，已经被广泛地应用到数字预失真技术的仿真与实现中，由于本文所提出的新型结构包含2 个预失真模块，故为了降低模型的复杂度，本文采用此模块进行仿真，大大降低了以Volterra 级数为模型的仿真计算量，并且由于非线性阶数为偶数时，MP模型产生的非线性失真频段距离中心频段较远，可以用一个设计良好的带通滤波器滤除[9]，功放产生非线性失真的主要因素是其模型的奇数阶所产生的频谱混叠和互调失真，故在使用MP 模型时，可以忽略其偶数阶的影响。式（14）可以重写为

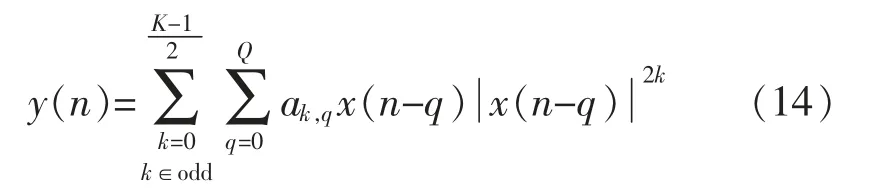
3 仿真分析

本文所提出的选择数字预失真结构采用Matlab进行建模仿真。输入信号采用的是由DMB 信号发生器所生成的符合国际标准的DMB 基带信号，其符号速率为3.072 MHz，采样率为8.192 MHz，信号的采样点数为40000 个，设置收敛因子的值为0.2，预失真结构采用提出的选择预失真结构。在整个仿真过程中，其模型系数是从实际的功放中提取出来的[10]。在记忆深度为3，非线性阶数为5 的条件下，提取出的模型参数如下：

根据提取的模型系数，本文对直接预失真模型、间接预失真模型和选择结构预失真模型在Matlab中进行了仿真实验，并通过以下几个方面进行比较和分析：①在记忆深度为3 和非线性阶数为5 的仿真条件下对以上3 种结构进行仿真；②在输入功率为2 dBm 的条件下，对3 种结构的收敛速度与收敛后的功率谱密度（power spectrum density，PSD）进行分析；③比较每种结构的收敛后的归一化均方误差大小。归一化均方均方误差的公式为

式中：N表示对输入信号的采样个数；y（n）为输入信号；y（n）mean为输入信号的均值。下面采用3 种结构，对比输入信号功率为2 dBm 的仿真结果，其中N取4096。其误差信号比较如图5所示。

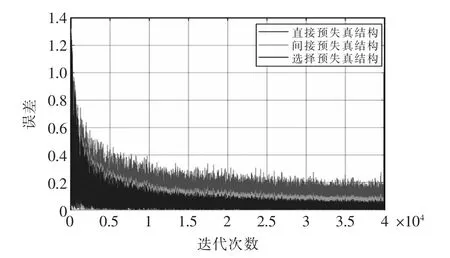
图5 误差信号比较Fig.5 Error comparison

采用选择预失真结构的预失真系统，约在第25000 个采样点收敛，其收敛速度与直接型预失真结构相差无几，但其收敛后的误差信号大小远小于直接型预失真结构收敛后的误差大小，约为0.1 个单位，且比间接型预失真结构的稳态误差要小约0.01 个单位。其收敛后的3 种结构的功率谱密度如图6所示。

图6 收敛后3 种结构的功率谱密度Fig.6 Power spectrum densities of three structures

功率谱密度图能够非常直观的描述预失真系统的效果，其中归一化频率的单位为MHz；幅度单位为dB，可以从图中基带信号频段以外的频段观察信号的衰减状况，根据图6所示，选择预失真结构的带外抑制效果要好于直接型预失真结构约3 dB，而与间接预失真结构的带外抑制效果相差无几。下面对3 种结构的归一化均方误差进行仿真，测试次数为8 次，仿真结果如表1所示。

表1 NMSE 测试结果Tab.1 Test results of NMSE

本文提出的选择预失真结构的收敛后归一化均方误差值均小于直接型结构和间接型结构，分别为7 dB 与2 dB 左右，对于功放模型的拟合度更好。

4 结语

本文提出了一种新型的选择预失真结构系统，功放模型采用的是记忆多项式模型。第一个改进是合并了两种结构的特点，利用收敛速度更快的NLMS 自适应算法调节2 个预失真模块的复增益系数；第二个改进是提出了一种通过比较器与一个二选一选择器所构成的新的数据迭代方法，其结构简单，延迟小。仿真结果表明，相较于现有的预失真结构，改进后的预失真结构的收敛速度与直接预失真结构相差无几，但其收敛后的误差比直接型与间接型两种结构都小，分别为0.15 个单位与0.03 个单位，且带外抑制效果更好，带外衰减相较于以上两种结构提高了约2 dB。