有限长波浪形圆柱绕流数值模拟
赵桂欣,桂洪斌,王晓聪
(哈尔滨工业大学(威海)船舶与海洋工程学院,山东 威海 264209)
作为一种经典的钝体绕流物理现象,圆柱绕流现象广泛存在于自然界中,流体经过圆柱时,会产生周期性脱落的漩涡,漩涡脱落使圆柱受到流体的脉动载荷从而导致结构振动[1],当结构振动严重时,会导致结构疲劳甚至损坏[2],造成损失.降低结构受到的脉动载荷,抑制结构体振动、减少结构损坏,在工程实际应用中有很大的意义.如何有效的减阻抑振是圆柱绕流问题的研究热点.
目前应用于圆柱绕流上的减阻抑振方法主要有主动控制和被动控制两种,被动控制不需要额外的能量输入,应用比较方便[3],在圆柱绕流中主要通过破坏圆柱体表面的压力分布以改变圆柱体受力[4],来达到减阻抑振的效果.波浪形圆柱采用改变圆柱外形的方法来破坏圆柱体表面的压力分布,具有减阻抑振的效果[5-6].
现有的波浪形圆柱的减阻抑振研究主要集中于无限长边界条件下,然而实际工程中,大多数的圆柱结构是有限长的,其周围的流场受到固定壁面和圆柱自由端面的影响,与无限长时相差很大,因而只分析无限长边界条件下波浪形圆柱减阻抑振的效果不能满足工程需要.考虑到实际工程中的流动大多处于亚临界流动区域,本文在对无限长圆柱绕流分析和有限长圆柱绕流分析[7-8]的基础上,采用大涡模拟的方法,对Re=3 900时的有限长波浪形圆柱绕流进行了数值模拟,研究波浪形圆柱减阻抑振的机理并得出一定组合情况下减阻较好的圆柱波浪外形.
1 数值模型
1.1 控制方程
本文中流体湍流模型采用大涡模拟[9]的形式,大涡模拟通过滤波函数将大尺度和小尺度涡分离开,大尺度的涡直接模拟,小尺度的涡选用亚网格尺度(SGS)模型来封闭.经过滤波函数处理后,不可压缩黏性流体的控制方程Navier-Stokes方程和连续性方程分别为:
(1)
(2)
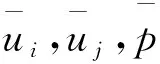
(3)
(4)
式中:δij为Kronecker符号;τkk为亚网格尺度应力各向同性部分;μsgs为亚网格湍流黏度.
1.2 几何模型
选用的波浪形圆柱几何外形如图1[10]所示,它的直径定义如下:
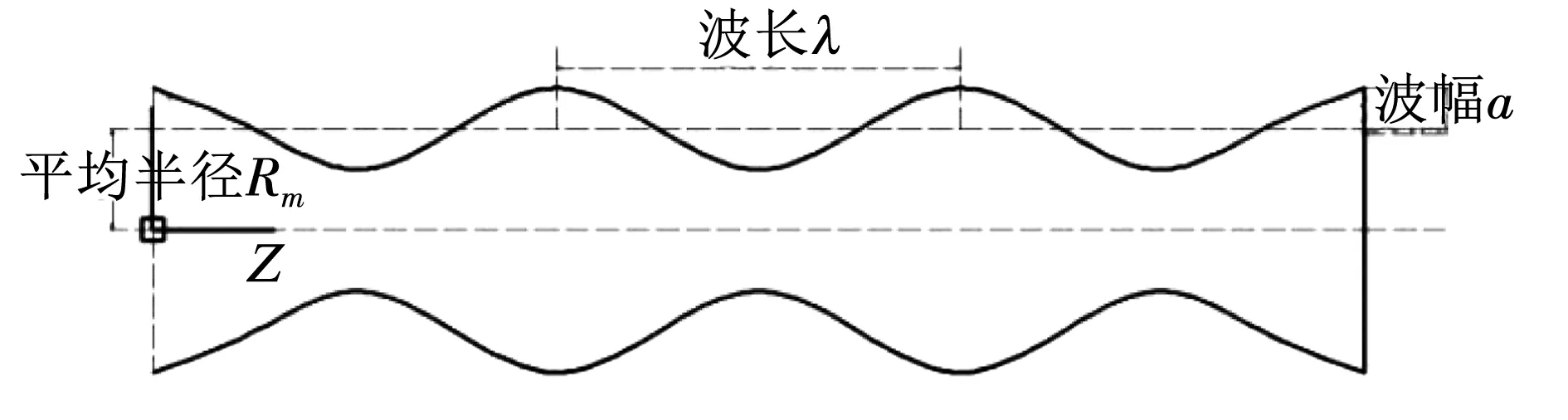
图1 波浪形圆柱外形示意
Dz=Dm+2acos(2πz/λ),
(5)
Dm=1/2(Dmax+Dmin).
(6)
式中:Dz为波浪形圆柱的直径;Dm为波浪形圆柱平均直径;a为波浪形圆柱表面的波幅;λ为波浪形圆柱表面波长.定义波浪形圆柱的最小直径处为马鞍面(saddle),最大直径处为节点面(noddle)[11].
为对比波浪形圆柱的减阻效果,本文选用的直圆柱直径为Dm,长度与波浪形圆柱长度相同,保证波浪形圆柱与直圆柱有相同的阻塞比.
将圆柱(直圆柱或波浪形圆柱)模型放入20Dm×10Dm×(3λ+3Dm)的流体域中,形成计算域几何模型,如图2所示,原点在底面圆心处,x方向为顺流向,y方向为横流向,z方向为展向.圆柱底面圆心距离速度入口为5Dm,距压力出口为15Dm,圆柱顶面即自由端面距流体域顶面为3Dm,以保证圆柱后方以及圆柱顶端流场的发展.

图2 圆柱绕流流场示意
波浪形圆柱网格划分如图3所示,直圆柱的网格划分与波浪形圆柱的网格划分方式相同.圆柱周围为O型网格,圆柱近壁面网格大小为0.001Dm,圆柱周围网格通过指数分布律进行局部加密,越靠近圆柱网格越小,以便捕捉圆柱体周围流动情况.
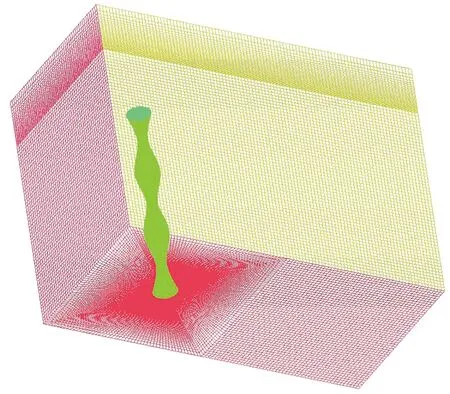
图3 网格划分
1.3 边界条件和计算工况设置
流场的边界条件设置如图2所示,设置速度入口,压力出口,流体域底面为固定壁面,顶面及两侧面为自由滑移壁面,圆柱体表面均为固定壁面.
流体的进口速度U0满足以圆柱平均直径Dm和动力黏性系数μ为特征的雷诺数为3 900.
在大涡模拟(LES)问题的计算过程中,时间步的选择要使库朗数(Courant number)在0.5~1.0范围内,C=uΔt/Δx,其中:Δt为时间步,Δx为网格尺寸,u为流体速度. 选择Δx为最小网格尺寸,u为来流速度U0.计算时间步取2.5×10-3s,相应库朗数为0.975,满足计算条件.
在计算工况选择时,为分别研究波浪形圆柱波长及波幅的影响,选择不同的波长和波幅进行组合,波浪形圆柱的高度为3λ[12],波长选择有3种:λ/Dm=2、3、4,波幅选择有4种:a/Dm=0.05、0.10、0.15、0.20.λ/Dm和a/Dm分别是波长和波幅的量纲一的量.为研究不同波长及波幅下的减阻作用,设置高度L为3λ的光滑有限长直圆柱做对照组,根据无因次波长为2,3,4,将直圆柱工况对应设定为C2,C3,C4.波浪形圆柱的工况组合见表1.
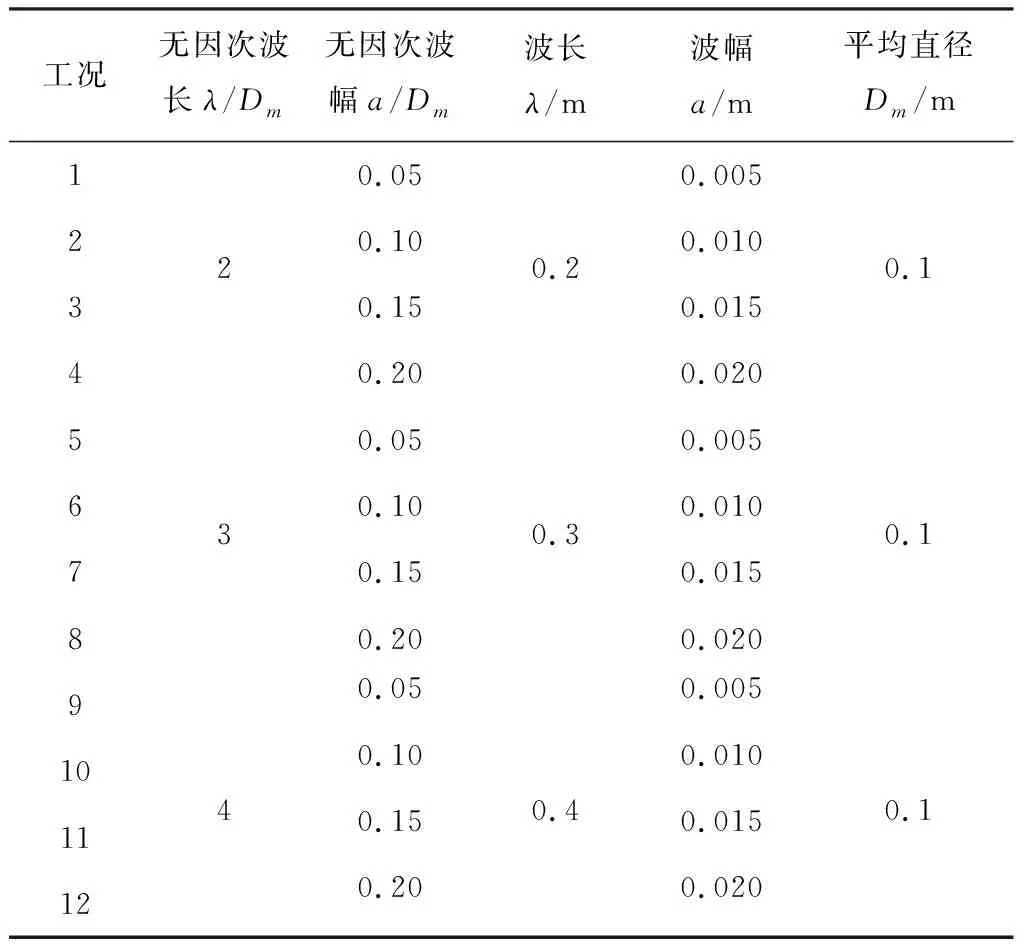
表1 波浪形圆柱计算工况设置
1.4 模型验证
计算在ANSYS Fluent流体计算软件中进行,压力速度耦合采用SIMPLE算法,对流项为二阶离散格式,扩散项为二阶中心差分.
为保证计算结果的有效性,将计算结果与文献[13-15]所做的实验、数值模拟结果进行对比验证,有限长直圆柱的验证结果见表2,其中:AR为长径比;Sim1、Sim2、Sim3为不同网格下的数值模拟结果;Exp1、Exp2和Exp3分别为实验结果,它们的阻力系数均值见表2,从结果可以看出,Sim2与Sim3数值模拟的结果与实验结果相差不大.为减小计算时间选择网格数量相对较少,计算结果与文献值接近的Sim2网格进一步对流场的计算结果进行验证.本次计算中有限长直圆柱的雷诺数选择为3 900,为保证计算结果的准确性,同样寻找雷诺数为3 900时的文献[16]计算结果,并进行对比,流场的计算结果与文献[16]中的结果如图4所示,从图4中曲线可以看出,模拟得到的结果与文献中的结果曲线趋势一致,计算结果相差不大,证明模拟的有限长圆柱计算结果是可靠的.
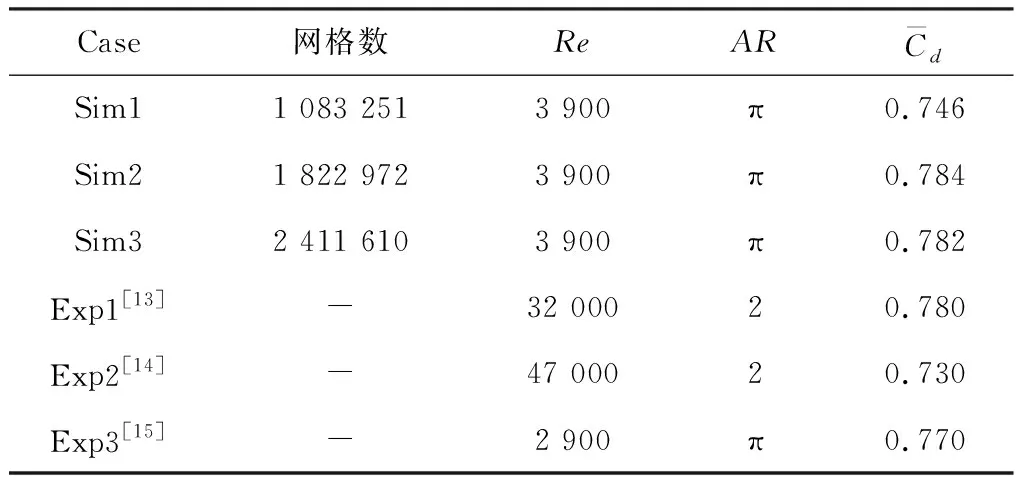
表2 有限长圆柱计算验证
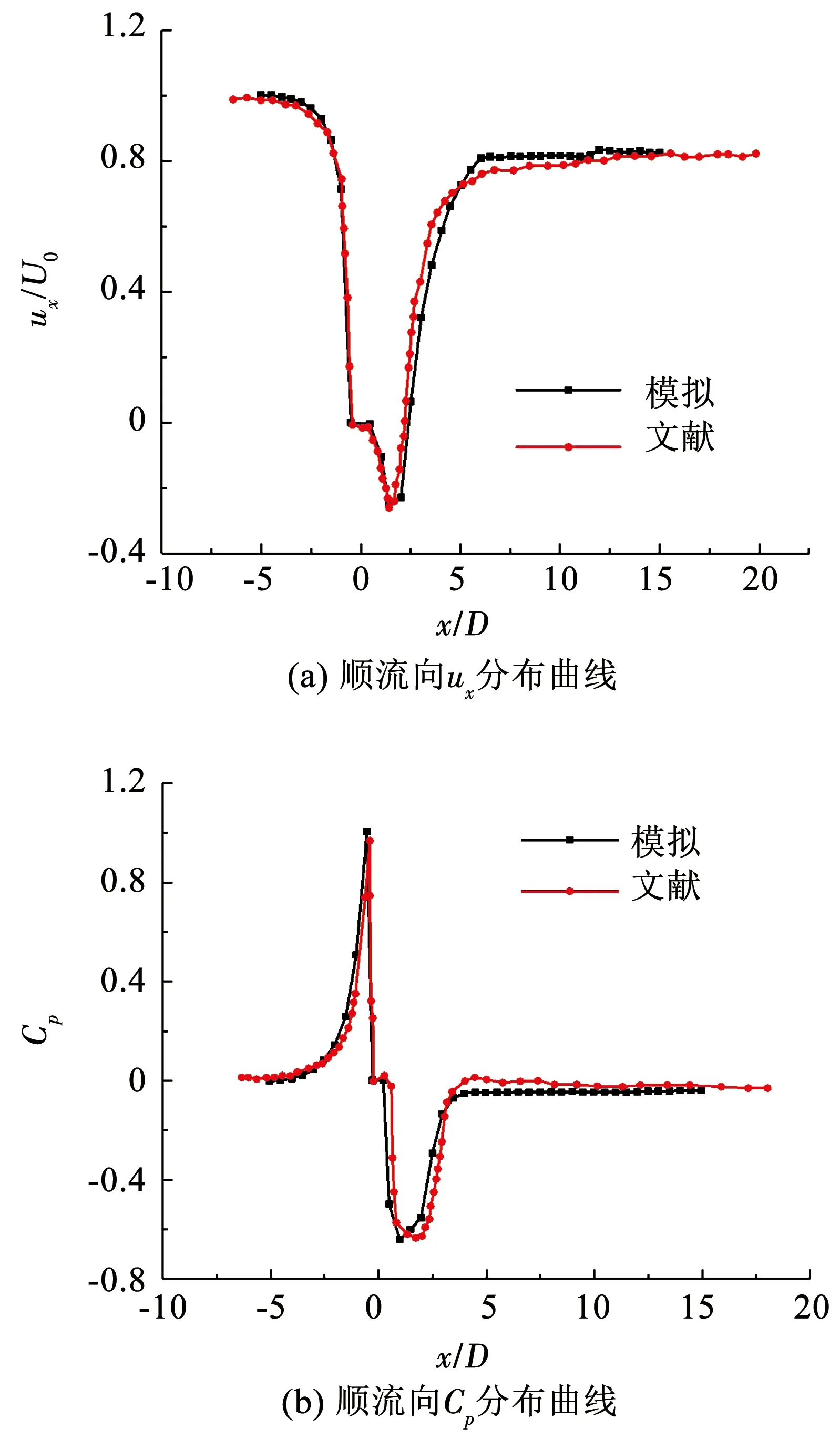
图4 有限长圆柱流场参数ux、Cp分布曲线
对波浪形圆柱计算进行验证,得到图5所示,其网格划分方式与Sim2相同,图片中WY-A和WY-B分别是雷诺数为3 000时a/Dm=0.091和a/Dm=0.152的文献中计算结果[12],其余为本文中数值模拟雷诺数同样为3 000时的计算结果,a/Dm略有差异,但差别非常小,在0.01之内.从图中可以看出,模拟得到的结果与文献中的结果曲线趋势一致,数值相差不大,说明波浪形圆柱的计算结果同样比较可靠.
2 结果及分析
2.1 时均流场
图6为λ/Dm=2、3、4的波浪形圆柱与相同长径比(L/Dm)的直圆柱的升、阻力系数在雷诺数Re=3 900时的对比曲线,直圆柱的波幅a可以看做为0,将之无量纲化可得a/Dm=0.
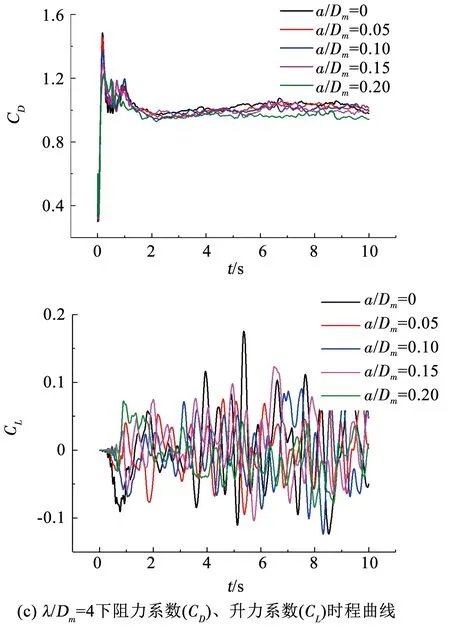
图6 各波长下圆柱升、阻力系数时程曲线
对于升力时程曲线,无论波浪形圆柱还是直圆柱其升力曲线都波动复杂并且无规律,这是有限长圆柱绕流特有的性质.对于阻力时程曲线,在阻力达到稳定时波浪形圆柱和直圆柱的阻力系数都围绕一均值上下波动.
为了进一步研究波浪形圆柱的波长和波幅对圆柱升、阻力产生的影响,根据已经得到的时程曲线得到阻力系数均值与升力系数均方根值并作图,3个作对比的直圆柱计算结果为C2、C3、C4.从阻力系数图7(a)中可以看出,无因次波长λ/Dm=2时只有a/Dm=0.10工况下波浪形圆柱阻力系数比直圆
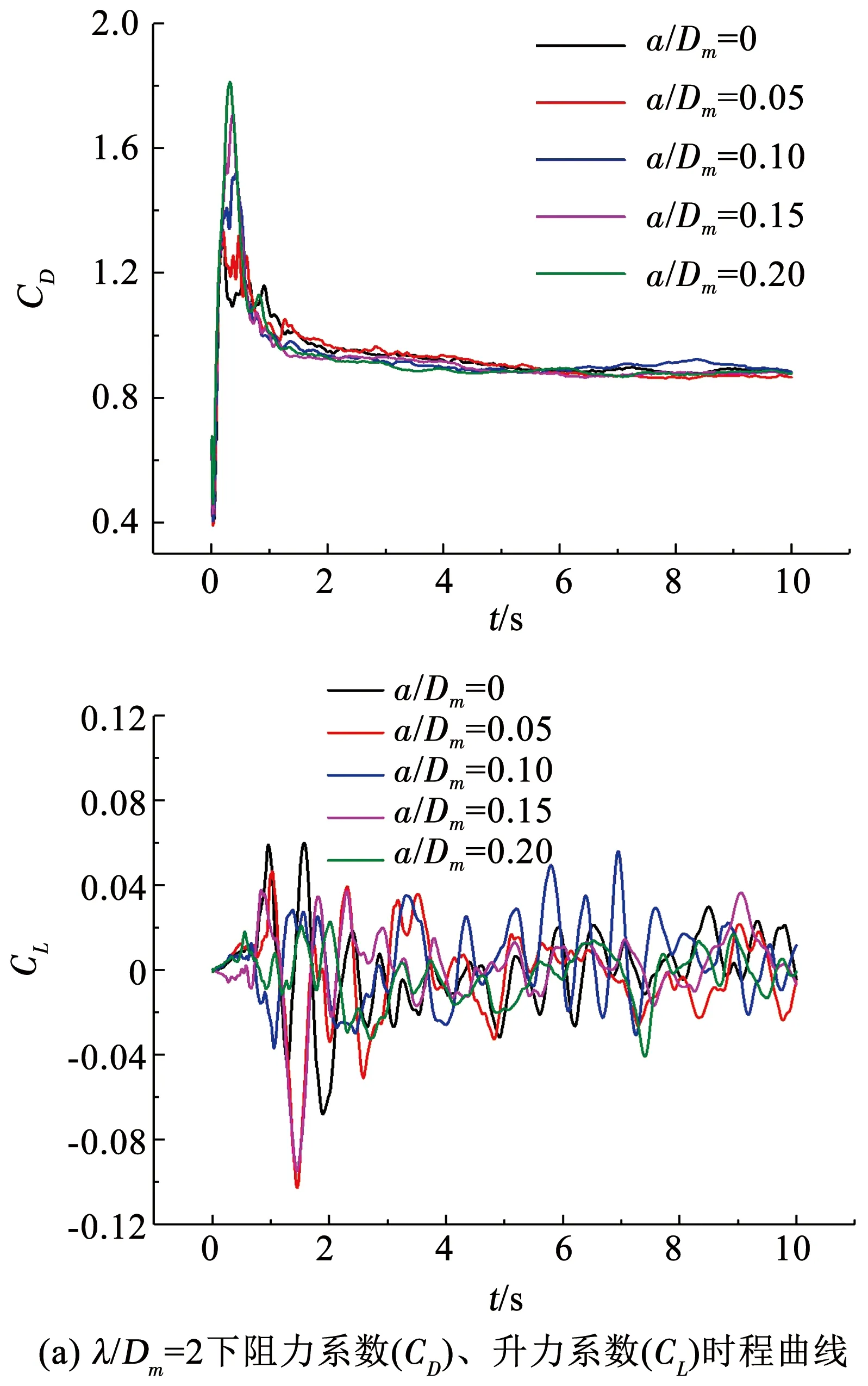
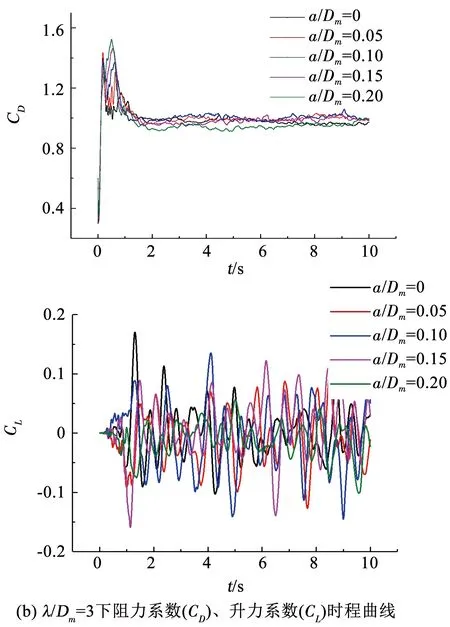
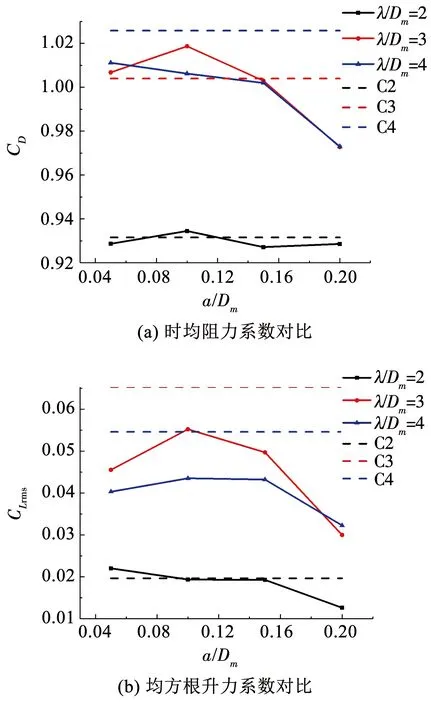
图7 波浪形圆柱时均阻力系数和均方根值升力系数对比图
柱大,其余3种工况波浪形圆柱阻力系数均有降低,但降低程度较小,降低约0.31%~ 0.48%左右;λ/Dm=3时,当a/Dm≥0.15工况下波浪形圆柱阻力系数降低明显,其中在a/Dm=0.20工况下阻力系数降低3.11%;λ/Dm=4时,4种波幅均能较大程度减小阻力系数,最大降低5.36%.由此可见,波长相同时不是所有波幅都能起到减阻效果,不同的波幅在不同波长下的减阻效果也不同.在本次计算的12种工况中λ/Dm=4,a/Dm=0.20时的工况计算减阻效果最好.
升力系数均方根值如图7(b)所示,圆柱体受到流体作用的升力,升力均方根值越大,升力的波动程度越大,结构体振动越剧烈.从图中可以看出大多数工况下相对于直圆柱,波浪型圆柱的升力系数波动减小.当波长λ/Dm=3、4时,升力系数均方根值明显减小,最高可减小40.9%~54.1%,能更有效的抑制升力波动.这说明在该圆柱外形下,流体漩涡的发展与脱落受到了抑制并发生改变.
从圆柱压力系数最小处对应的角开始研究圆柱周围的漩涡发展,按从下到上的顺序将波浪形圆柱的马鞍面、节点面命名为Saddle1、Noddle1、Saddle2、Noddle2、Saddle3,Saddle1为最底端的马鞍面.定义圆柱前方靠近速度入口处为0°,顺指针方向为角度增长的方向,做不同位置处圆周压力曲线,并定义圆周压力最低点处对应的角为θsep,可得到表3中直圆柱和波浪形圆柱的θsep.其中a1、a2、a3、a4分别表示a/Dm为0.05、0.10、0.15、0.20时的工况.从表中可以看出,直圆柱的θsep在展向发生的变化较小,变化幅度最大在2°~3°左右,而波浪形圆柱的θsep波动幅度较大,以a4、λ/Dm=4时的结果为例,θsep最大可相差6°,并且位于马鞍面处的θsep明显小于节点面处的θsep.

表3 各波长下不同波幅的圆周压力系数最小值对应角
为更加直观的观察到圆周压力系数随角度的变化以及圆周压力系数最低点对应角度的差异,现在此展现C4(波幅为0)以及波幅为a4、λ/Dm=4时的圆周压力系数曲线如图8所示,θ为角度,从图中可发现直圆柱压力系数最低点处对应的角度即θsep在不同高度上相差不大,波浪形圆柱不同高度上的θsep存在明显差异,马鞍面处的值明显小于节点面处的值,这说明在流体流经圆柱时节点面处压力系数先到达最低点,这种节点面与马鞍面处圆周压力最低点对应的角度的差异会影响圆柱在该位置处的前后压差,影响圆柱壁面上的流动,从而影响圆柱尾涡脱落,影响圆柱后方漩涡的发展,使波浪形圆柱为流漩涡与直圆柱尾流漩涡不同,从而使波浪形圆柱的升、阻力与直圆柱不同.
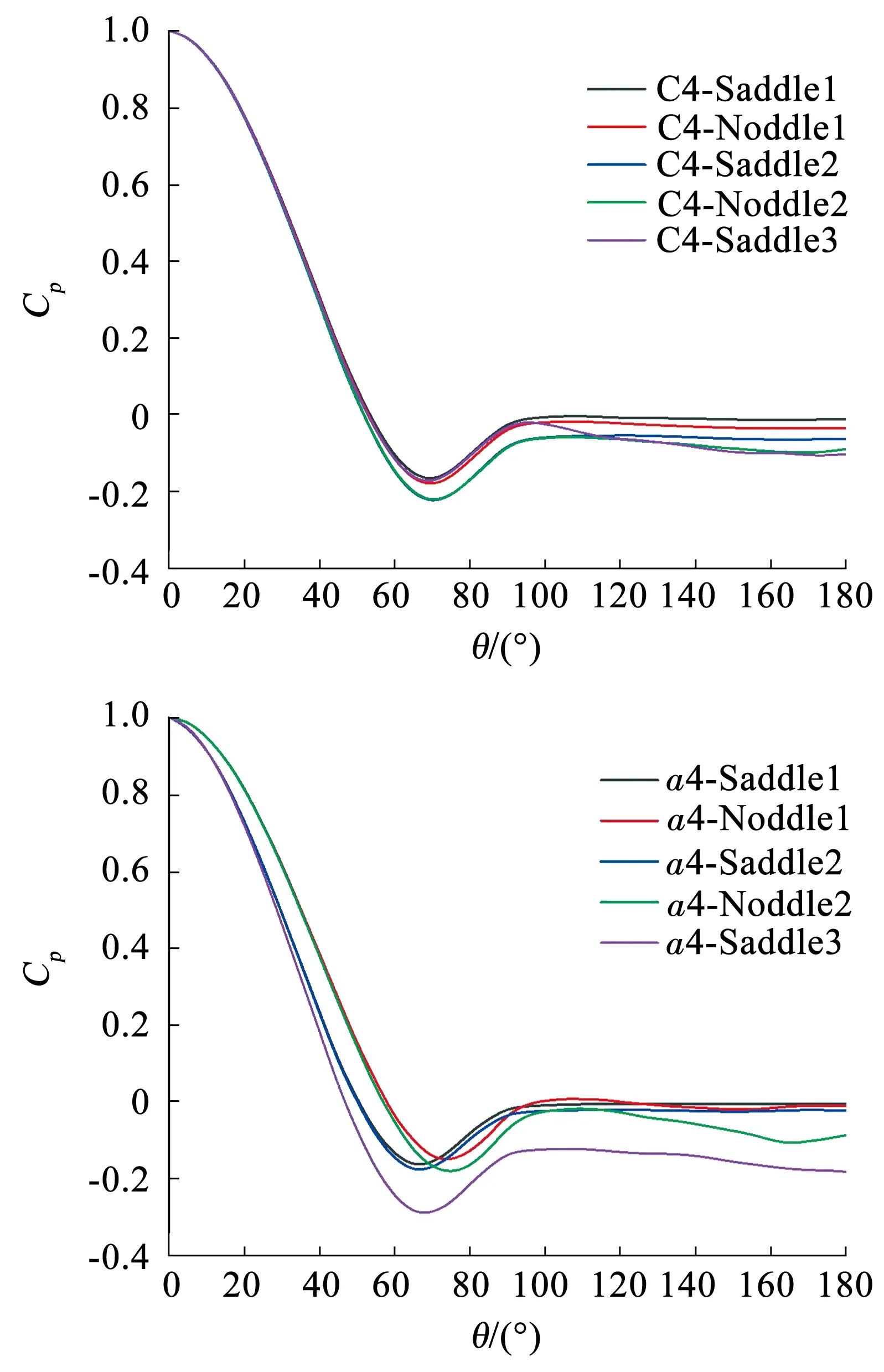
图8 λ=4Dm时直圆柱(C4)和波浪形圆柱(a4)圆周压力系数分布对比
从图8还可以发现经过θsep后随角度增大圆周压力系数明显上升,到达一定角度后圆周压力系数不再上升,该角度即为流动的分离角,直圆柱的分离角相差不大,在波浪形圆柱中马鞍面处分离角较小,节点面处分离角较大;这种分离角的差异是由于旋涡分离存在差异引起的,它影响波浪形圆柱后方旋涡脱落,使波浪形圆柱升阻力与直圆柱存在差异.
2.2 瞬时流场
为研究波浪形圆柱减阻抑振周围流场流动机理,现以本次计算中减阻抑振明显的工况12为例,用C4工况做对比,作出两种工况的涡量图和在马鞍面和节点面高度处的基于Q涡准则的涡量等值线图和圆柱涡量图,得到图9.
从图9中可以看出,从总体而言,有限长的波浪形圆柱和直圆柱靠近自由端处的下游流场都受到自由端面的影响呈现为“三角形”,体现了有限长圆柱绕流的圆柱后方流场特征;自由端上方漩涡分布复杂,从图9(b)可发现,在自由端顶部两圆柱上都有涡产生,被称为“顶涡”;流体流经自由端后,继续向圆柱后下方发展,形成“梢涡”产生下洗作用,影响圆柱的尾涡分布;从图9(a)中的涡量等值线可以发现在底部圆柱的固定端处,两圆柱前缘都出现“马蹄”形状的涡,该涡被称为马蹄涡.这说明有限长的波浪形圆柱具有与直圆柱类似的流动特征.波浪形圆柱的流动具有其特有的性质,波浪形圆柱的直径不断发生变化,使波浪形圆柱的后方漩涡发展呈现出“分段”特性,使流经波浪形圆柱的流体流动更加复杂,并且从图9(c)中可发现相同的涡量准则下波浪形圆柱下游流场形成的涡长度更长,这说明波浪形圆柱的产生的尾流可以将形成的漩涡输送到离圆柱较远处,漩涡在距离圆柱更远的位置处耗散,在一定程度上削弱了漩涡的交替脱落,而交替脱落的漩涡是因起圆柱受到交替变化升力的主要原因,因此波浪形圆柱的流场特征决定了它受到较小的脉动升力,能更有效的减阻抑振.

图9 基于Q涡准则涡量图
沿水平方向做速度云图和流线图得到图10,其中L2、L4为节点面位置,L1、L3、L5为马鞍面位置.从图中可以看出马鞍面的回流区长度大于节点面回流区长度,对L3和L2处的回流区长度作差得到Lr并进行无量纲化处理可得到Lr/Dm=0.3,即马鞍面回流区长度比节点面回流区长度长0.3Dm.而直圆柱的回流区长度在两者之间并且在不同平面间相差不大.马鞍面更长的回流区使漩涡耗散过程发生在距离圆柱较远处,减弱了升力的波动,同时使圆柱基础压力系数较高,造成了阻力系数的降低.从波浪形圆柱各位置处的回流区宽度来看,节点面的回流区宽度明显小于马鞍面回流区宽度,更小的回流区宽度使节点面附近的分离剪切层获得了加速流动,而更宽的回流区使漩涡分离更加容易,这就是马鞍面处分离角更小的原因.从漩涡脱落情况来看靠近自
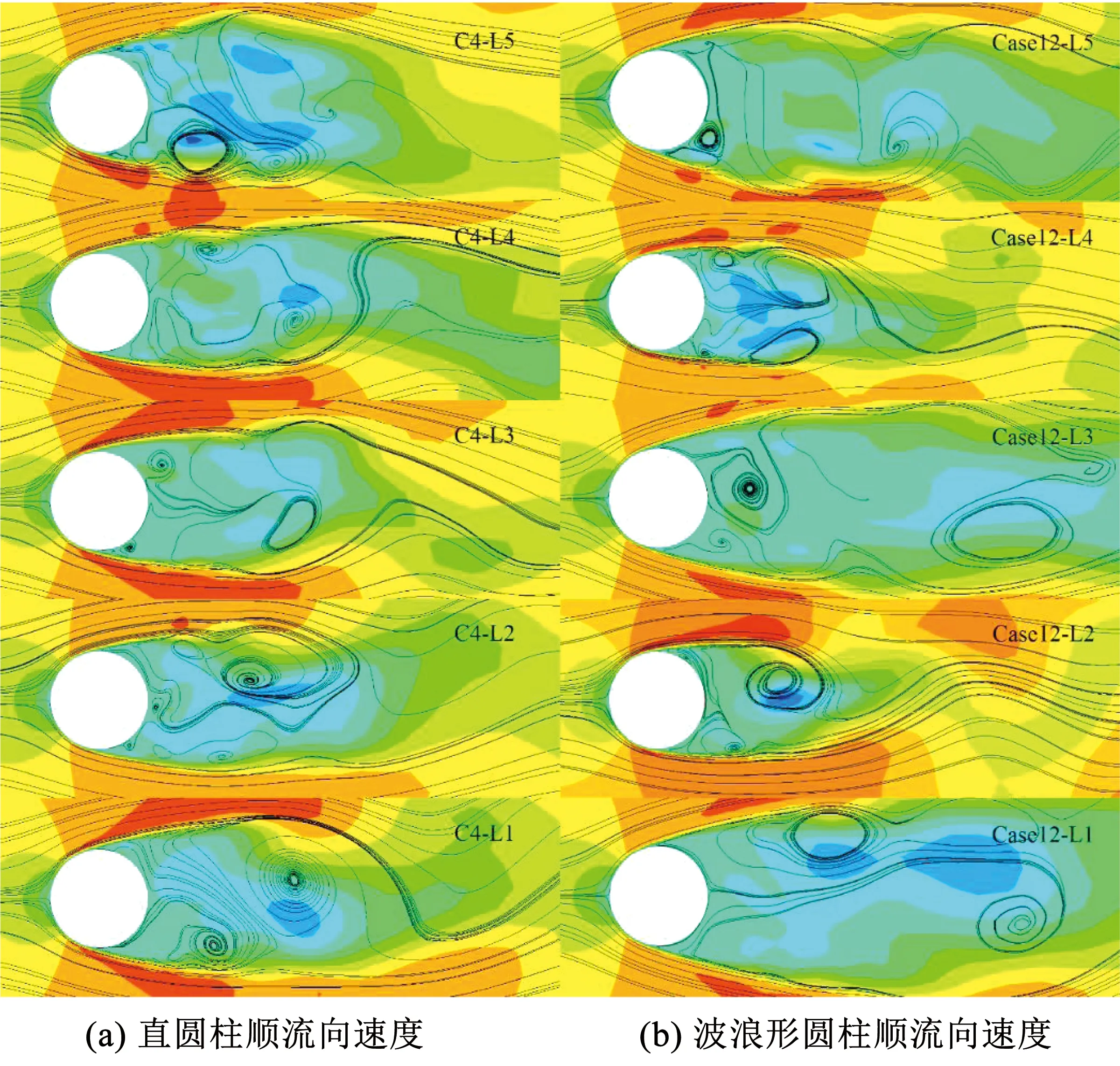
图10 直圆柱和波浪形圆柱顺流向速度云图对比
由端面处的L5与其他高度上的漩涡脱落形式有明显差异,这主要受到自由端面下洗作用的影响,是直圆柱和波浪形圆柱共有的流动特征,但是二者的漩涡脱落形式却不同,这是由于圆柱波形的存在影响了下洗作用产生的涡,使波浪形圆柱周围的流动更加复杂.
从图11近壁面流线继续分析波浪形圆柱能减阻抑振的原因.流线的交汇处即为流动的分离线.沿圆柱展向直圆柱的分离线大致成一条直线,而波浪形圆柱的分离线有较小幅度的波动,这与图8中分离角统计结果一致.局部放大波浪形圆柱壁面流线,发现流经马鞍面的流体除向圆柱后方流去的尾流外,还有一部分向两侧的节点面流去,形成了展向上的流动,而直圆柱只有极少部分流体在展向上发生流动,波浪形圆柱壁面流体展向交互运动严重扰乱了展向各位置的尾流形成过程,在一定程度上改变了尾流场,抑制了升力波动,造成了阻力损失,使波浪形圆柱阻力系数降低.

图11 圆柱近壁面流线图
3 结 论
1)采用大涡模拟的方法计算得到了有限长直圆柱的阻力系数、顺流向速度、压力分布与波浪形圆柱的阻、升力系数,得到的计算结果与文献中结果对比发现吻合良好,表明大涡模拟的方法可准确模拟有限长波浪形圆柱问题.
2)有限长波浪形圆柱与有限长直圆柱受到的升、阻力系数时程曲线变化趋势基本一致,升力系数时程曲线均波动剧烈无规律,体现有限长圆柱的流动性质;但二者阻力系数均值与升力系数均方根值存在差异,与有限长直圆柱相比,12种波浪形圆柱中有9种阻力系数均值降低约0.31%~5.14%,11种工况下的升力系数均方根值降低,降低幅度最高达54.1%,升力系数均方根值降低可起到抑振作用;说明在一定波幅和波长下波浪形圆柱具有较好的减阻抑振作用.从升阻力系数的降低幅度来看,圆柱外形对升力系数的影响程度较大.
3)有限长波浪形圆柱存在与有限长直圆柱相似的流动特征,二者均存在顶涡、梢涡和马蹄涡;波浪形圆柱近壁面展向,流经马鞍面的流体一部分向节点面流去,影响漩涡脱落,使波浪形圆柱马鞍面处圆周压力系数最低点对应角比节点面处小,影响尾流形成,抑制升力波动,造成了阻力损失,起到减阻抑振的作用;同时,波浪形圆柱马鞍面处有更宽、长的回流区,更宽的回流区使马鞍面处分离剪切层速度比节点面处小,漩涡分离更加容易,更长的回流区使漩涡耗散发生在距离圆柱更远处,减弱了升力波动.

