多离散变量桁架结构协调优化研究*
张志强 秦义校 谷金朋
太原科技大学机械工程学院 太原 030024
0 引言
臂架为典型的细长桁架结构,是履带起重机的主要承载构件,在较大载荷作用下易发生几何非线性行为,使臂架变形过大而失稳。因此,质量轻、承载力高的臂架对保证履带起重机的工作性能非常重要。基于不同的优化设计方法和分析软件,国内外学者对桁架式臂架结构进行了许多研究。文献[1]从1968年~2014年介绍了具有离散设计变量的桁架结构优化的模型,理论和数值方法。该领域的文章全面收集,其研究方法已从确定性方法转变为元启发式方法,即随机方法搜索方法。文献[2]将基于生物地理学的优化(BBO)和差分演化(DE)方法进行混合,优化具有连续和离散变量的桁架结构的设计。文献[3]提出一种自适应精英差分进化算法(aeDE),用于优化具有离散设计变量的桁架结构。通过6个具有离散设计变量的桁架结构优化问题,证明了该方法的有效性和可靠性。文献[4]充分考虑起重机失稳因素,进行了结构振动和失稳分析,为其合理安全设计提供了理论基础。文献[5]提出一种面向对象的桁架臂架建模方法,为桁架臂架系统仿真设计提供了方法基础,并以全地面起重机桁架副臂为例,验证了该方法的正确性和可行性。
由于本文中的最佳动臂尺寸受特定运输条件和制造模型的限制,故选择此模型中最大的动臂。图1为优化的复杂桁架,动臂总长为120 m,底部两个下部铰接点之间的距离为2.2 m,且动臂顶部的横截面较小。
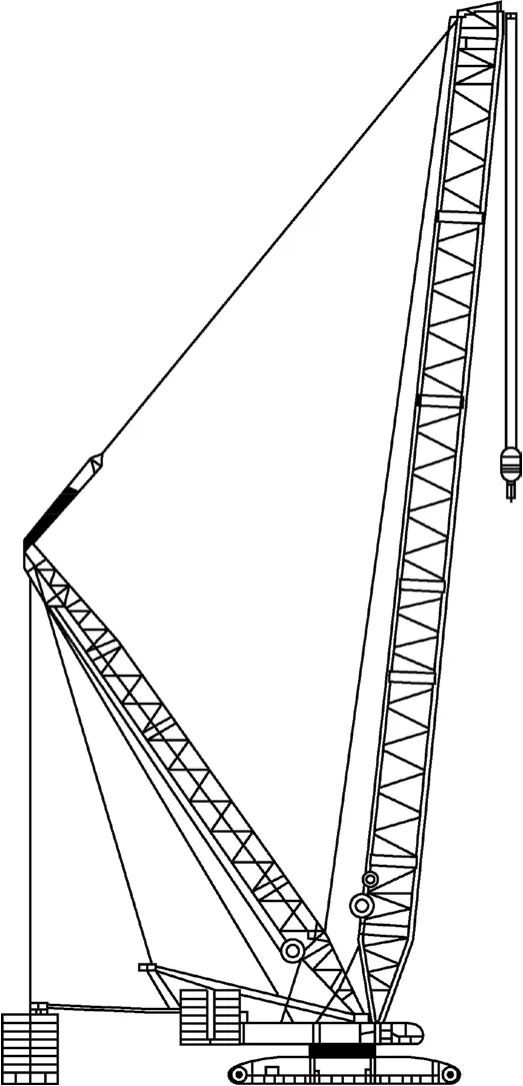
图1 履带起重机臂架结构示意图
图2为要优化的动臂部分的离散变量。本文将非线性有限元法和非均匀离散变量协调优化法相结合,解决了复杂桁架工程的实际问题,编写了程序以方便广泛应用。研究结果表明,该优化算法在解决工程问题时的应用思想和数学模型建立方法具有重要的参考价值。
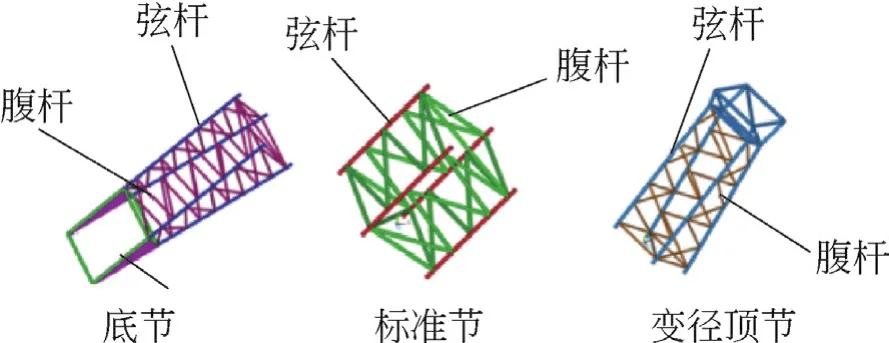
图2 臂架各节中的设计变量
1 智能优化算法与桁架臂的优化模型
1.1 智能算法
智能优化算法对要解决问题的目标函数无特殊要求,并可处理离散变量问题和连续变量问题。该方法属于改进的混合离散变量优化方法,其算法逻辑框图如图3所示。
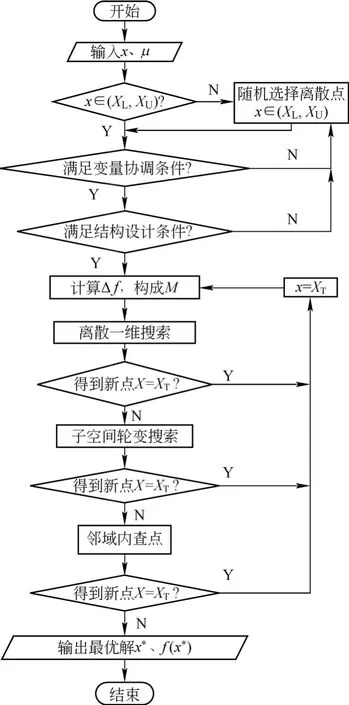
图3 优化算法逻辑框图
在工程优化设计中,大多数在数学编程中使用连续变量的约束非线性优化方法一般属于局部最优,而最优解总是在约束区域的边界上。非均匀离散变量的协调优化方法不仅可以避免上述缺点,还可大大加快初始搜索的速度。增加变量协调约束可使算法消除搜索过程中不满足横截面特征的值,例如腹板构件的外径不可大于弦杆的外径。
1.2 复杂桁架臂的优化数学模型
由于履带起重机主臂为组合空间结构,其单元种类和材料种类较多,导致该类结构按传统设计方法设计会造成材料浪费,体积增大,作业时产生过大惯性。
1)设计变量
以LR1300型履带起重机为研究对象,为优化提供初始设计,取底节支承杆、底节、标准节、变径顶节的设计参数为基本变量,具体如表1所示。
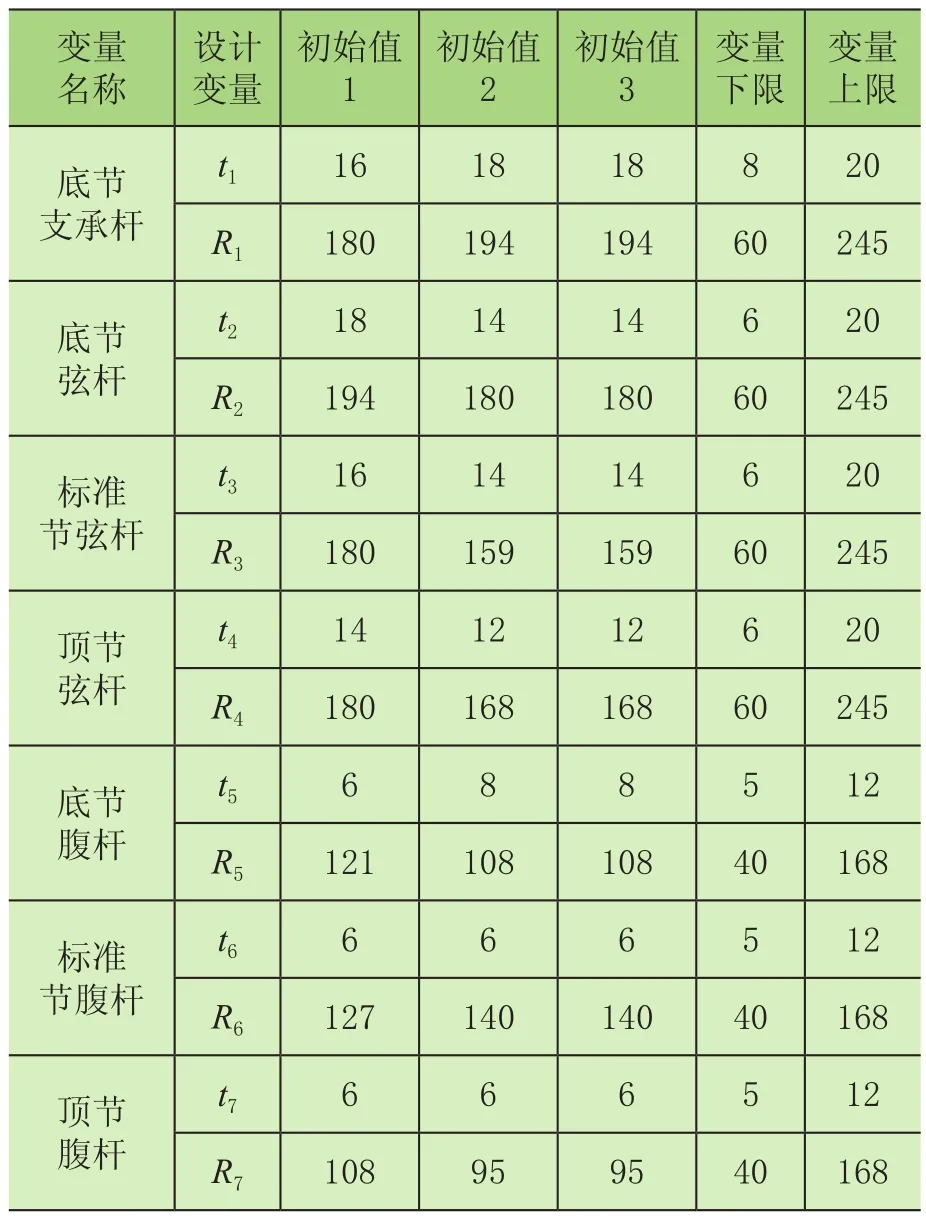
表1 设计变量不同的初始值及其上下限
2)目标函数
在满足所有约束条件的前提下以降低结构总质量为目标,目标函数可写为
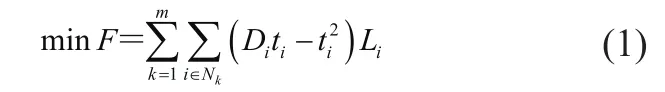
式中:Nk是属于第k组梁单元编号集合,Di为第i个杆单元的外径,Li为第i个梁单元的长度,ti为第i个梁单元的壁厚,Li第i个梁单元的密度。
如上t1、R1、t2、R2、t3、R3、t4、R4、t5、R5、t6、R6、t7、R7在VB优化程序中分别对应变量xi(i=1,2,…,14)。
3)约束条件
在主臂的优化过程中,算法每取得一组取值时都要验证满足结构设计规范的约束条件,而这些约束条件往往比较复杂,导致算法收敛速度较慢。在本文中,增加变量协调约束,并且在算法每取得一组取值时先验算这类约束条件,先剔除一部分取值。将以下所列的G1~G10作为变量协调约束加入VB优化程序中。
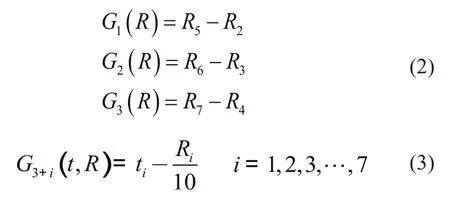
式中:G1~G3分别为第一类变量协同约束;G3+i为第二类变量协同约束。
在每次几何非线性分析之后,必须提取每组杆件的最大冯·米塞斯应力约束条件。在对于这种复杂应力结构应判定其Von Mises 等效应力,即
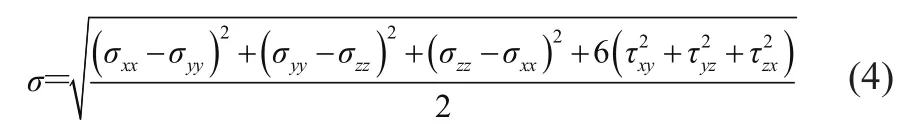
臂架在各种工况下承受不同的载荷组合,故分组杆件中的最大应力不得大于许用应力。臂架中底节支承杆最大应力为σ1,底节中弦杆最大应力为σ2,标准节中弦杆最大应力为σ3,顶节中弦杆最大应力为σ4,底节中腹杆最大应力为σ5,标准节中腹杆最大应力为σ6,顶节中腹杆最大应力为σ7,则有σ1< [σ]1,σ2< [σ]2,σ3< [σ]3,σ4< [σ]4,σ5< [σ]5,σ6< [σ]6,σ7< [σ]7,其中 [σ]i为各组杆件的许用应力。
臂架的结构形式复杂,承受的载荷和约束也较复杂,在臂架高耸时容易发生失稳。根据履带起重机臂架受力形式为双向压弯构件的原理,其整体稳定性验算公式为
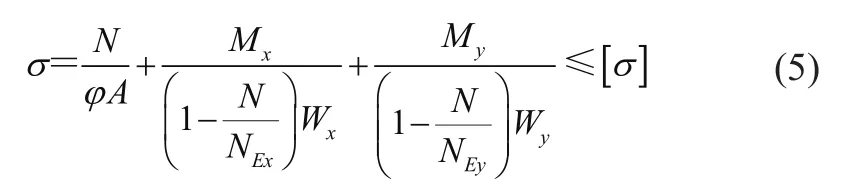
式中:N为臂架轴向力,Mx、My为臂架计算截面对x轴或y轴的弯矩,NEx、NEy为臂架对x轴或y轴的名义欧拉临界应力载荷,φ为臂架最大长细比选取的压杆稳定系数,A为臂架截面积,Wx、Wy为臂架截面对x轴或y轴的抗弯截面系数,[σ]为钢材的许用应力。
2 复杂桁架臂结构优化结果分析
选择3个不同的初始点进行优化,并比较优化前后的数据,详见表2~表4。本文分别取了3组符合结构设计规范的初始值进行优化,初始值1、2、3分别在迭代10次、9次、7次后得到收敛,收敛结果基本一致,故本文只对初始值为1时的优化结果进行讨论分析。
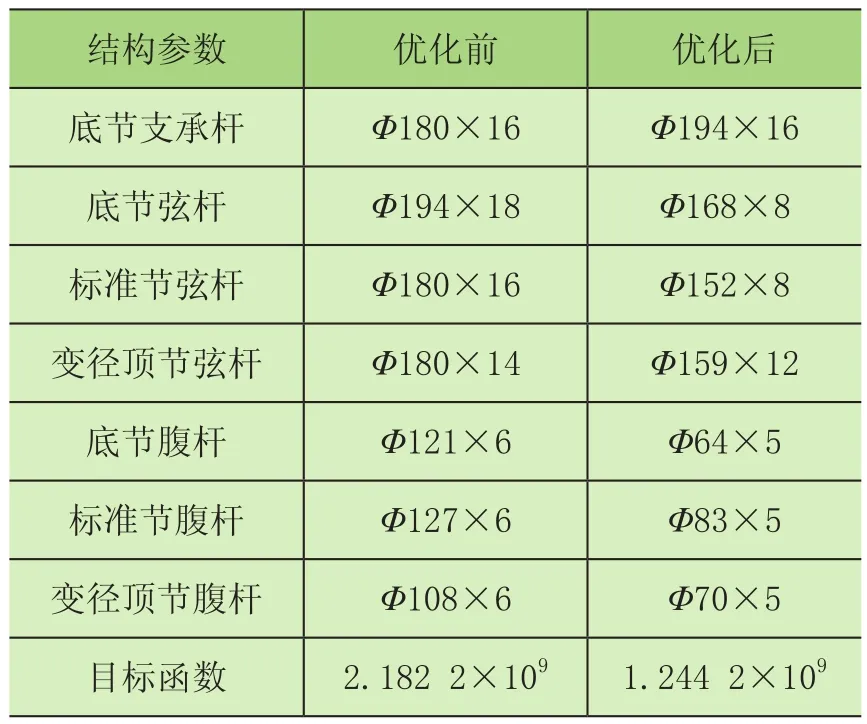
表2 初始值为1时的优化前后的结果对比
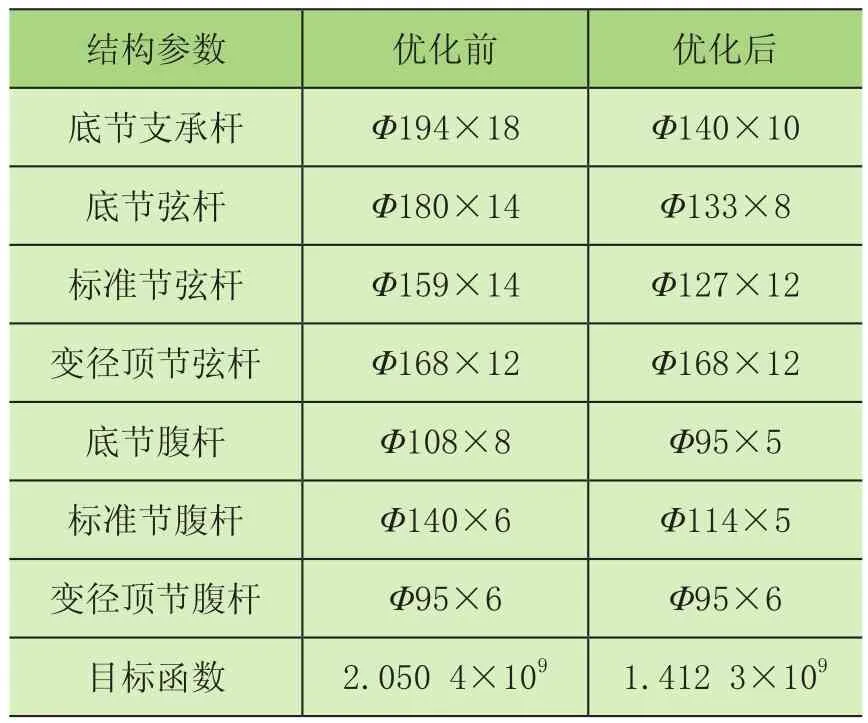
表3 初始值为2时的优化前后的结果对比
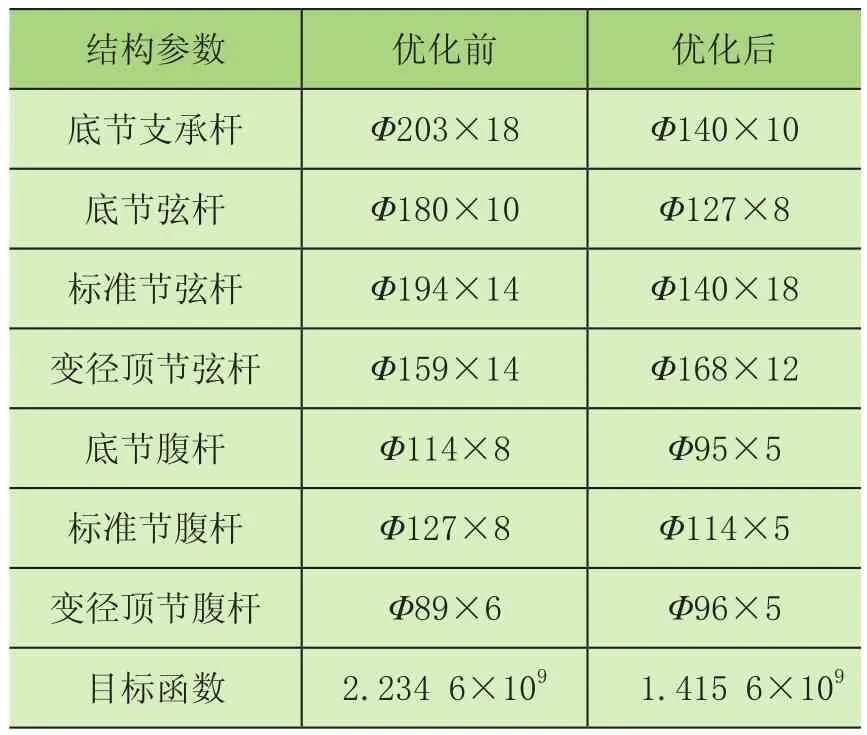
表4 初始值为3时的优化前后的结果对比
图4为所选初始值1下的变量优化历程图。其中,图4a为以各组杆件的壁厚为设计变量的优化历程,曲线x1、x3、x5、x7分别代表主弦杆、底节弦杆、标准节弦杆和顶节弦杆的壁厚,曲线x9、x11、x13分别代表底节腹杆、标准节腹杆和顶节腹杆的壁厚。从图中可以看出,代表弦杆壁厚曲线的变化率比代表腹杆壁厚曲线的变化率要高。图4b为以各组杆件的外径为设计变量的优化历程,曲线x2、x4、x6、x8分别代表主弦杆、底节弦杆、标准节弦杆和顶节弦杆的外径,曲线x10、x12、x14分别代表底节腹杆、标准节腹杆和顶节腹杆的外径。从图中可以看出,代表杆件外径的曲线呈下降趋势,会出现局部峰值。在优化过程中,当个别变量的取值较大时,就会有与其协调的变量来进行协调与制约。
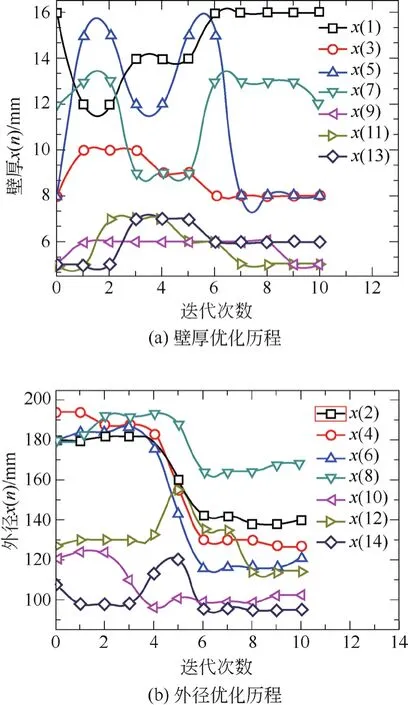
图4 初始值1时的圆管壁厚、外径优化历程
从整体来看,各变量在优化过程中的变化趋势均较正常,且体现了变量之间协调变化的特点。通过对优化结果的提取与分析可知,在用VB编写的优化程序中增加变量协调约束条件,使优化分析结果更接近实际工程应用,同时使复杂优化问题求解速度更快。
由目标函数优化历程与各类变量的优化历程分析可知,运用本文算法优化桁式臂架,其总质量总能达到一个最佳值,最多可减少26%,且臂架型材截面更加合理。为了验证上述优化结果,分别选取了初始值1下各节优化前后的应力图,如图5所示。在优化后,底节承载应力由111.55 MPa增加到228.8 MPa,标准节承载应力由137.58 MPa增加到271.7 MPa,变径顶节承载应力优化前后差别不大,这表明它充分利用了材料的承载能力。
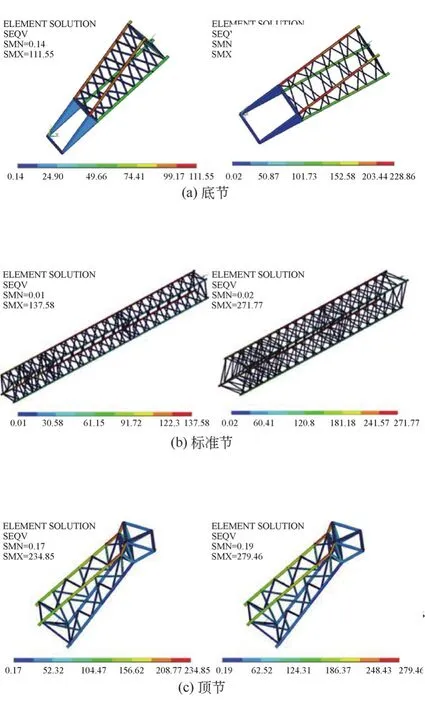
图5 各节优化前后应力图
3 结论
提出了将改进的离散变量智能优化算法与结构非线性有限元分析相耦合的复杂桁架工程优化方法,加快了复杂结构优化进程。通过对桁架臂工程实例的优化分析,可知本文解决复杂工程问题的方法为复杂桁架结构的优化设计提供了思路,在工程实践中具有一定的应用价值。

