气象用玻璃液体温度表校准结果的不确定度评定

刘海珍，东方，郑树芳，温晓辉

（1.内蒙古大气探测技术保障中心,内蒙古 呼和浩特 010051;2.内蒙古雷电预警防护中心,内蒙古 呼和浩特 010051）

引言

由于测量误差的存在，仪器的测量结果一般是以测得的量值及其不确定度来表示[1]。其中，不确定度是用来表示测量结果中测得值分散程度的一个重要参数，其量值是可被估算出来，并且量值的大小很大程度上反映了测量结果的可靠性[2]。所有的测量结果都不可避免地具有不确定度，也就是说，气象用玻璃液体温度表通过测量所给出的测量结果也具有不确定度。为了确保气象用玻璃液体温度表测量结果的准确性和可靠性，需定期对其进行检定或校准实验，并对测得的量值进行不确定度分析与评定。为此，本文应用温度表检定中现用的二等铂电阻温度计标准装置，以干湿球温度表为代表进行了此项分析。

1 校准方案

以干湿球温度表（其测量范围为-55～+30 ℃，最小分度值为0.2 ℃，MPE为±0.3 ℃）为研究对象，在温度为22.3 ℃、相对湿度为33%RH和气压为901.5 hPa的环境条件下，依据JJG207-92检定规程的要求对其进行校准实验。校准实验标准器选用二等标准铂电阻温度计，配套设备选择直流测温电桥和液体恒温槽。校准时，将二等标准铂电阻温度计和干湿球温度表同时固定于同一液体恒温槽内中央等高位置。将二等标准铂电阻温度计输出端与直流测温电桥输入端连接，分别打开二等标准铂电阻温度计、直流测温电桥和液体恒温槽。调节液体恒温槽，设定温度校准点，当液体恒温槽达到设定值时，稳定30 min后开始读数。本次实验选取+30 、0 ℃和-40 ℃三个校准点。

2 校准测量模型

由《JJG207-92气象用玻璃液体温度表检定规程》可知，干湿球温度表测量误差的计算公式为：

式中：T被为干湿球温度表的测得值；T标为二等标准铂电阻温度计的测得值。

对式（1）求偏导可得出干湿球温度表测量值的灵敏系数为1，二等标准铂电阻温度计测得值的灵敏系数为-1。

3 不确定度的来源与评定

通过对干湿球温度表以及干湿球温度表校准实验所采用的测量方法、测量设备和测量条件等方面的全面分析，可得出干湿球温度表在校准时其不确定度来源主要可分两大类：一类是由干湿球温度表引入的不确定度，另一类是由标准装置引入的不确定度。干湿球温度表引入的不确定度又主要是由干湿球温度表示值重复性和干湿球温度表分辨力引入的不确定度，标准装置引入的不确定度又主要是由二等标准铂电阻温度计固定点的稳定性、二等标准铂电阻温度计工作电流引起的自热效应、直流测温电桥、液体恒温槽内温度波动性、液体恒温槽内温度不均匀性、数据处理终端的修约误差引入的不确定度。

由《JJF1059.1—2012测量不确定度评定与表示规范》[3]可知，不确定度来源中，由干湿球温度表示值重复性引入的不确定度分量采用A类标准不确定度评定，其余分量采用B类标准不确定度评定。

3.1 由干湿球温度表引入的标准不确定度

3.1.1 由干湿球温度表示值重复性引入的标准不确 定度

根据校准方案的要求，将二等标准铂电阻温度计和干湿球温度表同时固定于同一液体恒温槽内中央等高位置，调节液体恒温槽，分别设定温度校准点+30、0 ℃和-40 ℃，当液体恒温槽达到设定值时，稳定30 min后，读取二等标准铂电阻温度计和干湿球温度表的示值，每2 min读取1 次，共读取10 次。由测量模型（式1）可计算出干湿球温度表各校准测试点的测量误差，由贝塞尔公式[3]（式2）可计算出干湿球温度表各校准测试点测量误差的实验标准偏差（s(x)），再由算术平均值实验标准偏差公式[3]（式3）可计算出干湿球温度表各校准测试点重复测量导致测量结果的A类标准不确定度（u11）。

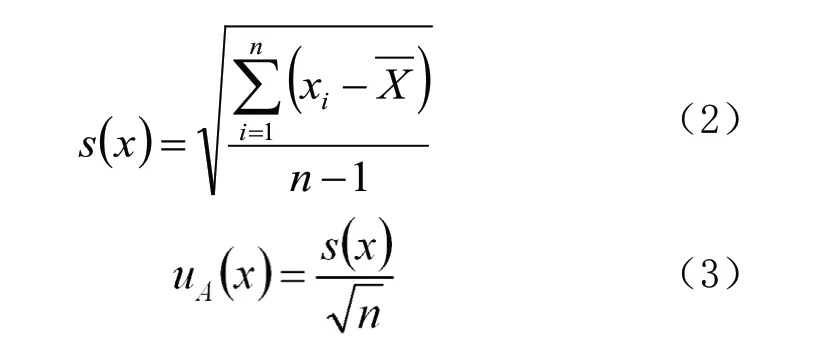
式中：xi为第i次测量的测量值；n为测量次数；X、Y为n次测量所得一组值的算术平均值；s(x)为n次测量中单次测量值的实验标准偏差；uA(x)为测量重复性导致的测量结果的A类标准不确定度。干湿球温度表示值重复性校准实验数据(表1)。

表1 干湿球温度表示值重复性校准实验数据

3.1.2 由干湿球温度表分辨力引入的标准不确定度

干湿球温度表最小分度值为0.2 ℃，其分辨力为0.2 ℃÷10=0.02 ℃，即区间半宽度为0.02 ℃，按均匀分布，取包含因子为，由B类标准不确定度评定公式[3]可计算出干湿球温度表分辨力引入的标准不确定度（u12）：

式中：uB为B类标准不确定度；a为区间半宽度；k为包含因子。

3.1.3 由干湿球温度表引入的标准不确定度

由于干湿球温度表示值重复性引入的A类标准不确定度分量和其分辨力引入的B类标准不确定度分量存在相关性，根据合成标准不确定度计算原则[4]可知，由干湿球温度表引入的合成标准不确定度（u1）为两者中较大分量的数值。

3.2 由标准装置引入的标准不确定度

3.2.1 由二等标准铂电阻温度计固定点的稳定性引入的标准不确定度

根据《JJG160—2007标准铂电阻温度计检定规程》[4]的要求可知，二等标准铂电阻温度计固定点的稳定性最大不超过：+30 ℃为8.0×10-3K、0 ℃为10.0×10-3K、-40 ℃为10.0×10-3K，即区间半宽度：+30 ℃为8.0×10-3K、0 ℃为10.0×10-3K、-40 ℃为10.0×10-3K，按均匀分布，取包含因子为 ，由式（4）可计算出其标准不确定度（u21）。

3.2.2 由二等标准铂电阻温度计工作电流引起的自热效应引入的标准不确定度

根据《JJG160-2007标准铂电阻温度计检定规程》[4]的要求可知，二等标准铂电阻温度计在水三相点（0.01 ℃）测量时，其产生的自热效应换算成温度值最大不超过4.0×10-3K，在校准点+30 ℃测量时，由于恒温槽中流动介质的温度较高，其产生的自热效应的影响可忽略不计，在校准点-40 ℃测量时，其产生的自热效应参考其稳定性，取值最大不超过10.0×10-3K，即区间半宽度：30 ℃为4.0×10-3K、0 ℃为0.0 K、-40 ℃为10.0×10-3K，按均匀分布，取包含因子为，由式（4）可计算出其标准不确定度（u22）。

3.2.3 直流测温电桥引入的标准不确定度

由《JJG160—2007标准铂电阻温度计检定规程》[4]的要求可知，直流测温电桥测量二等标准铂电阻温度计的相对误差不大于1.0×10-5，二等标准铂电阻温度计的扩展不确定度为Urel=1.0×10-6，远优于规程要求，其引入的标准不确定度（u23）可忽略不计。

3.2.4 液体恒温槽内温度波动性引入的标准不确定度

根据《JJG207—92标准铂电阻温度计检定规程》的要求可知，液体恒温槽内温度波动度≤±0.02 ℃，即区间半宽度为0.02 ℃，按均匀分布，取包含因子为，由式（4）可计算出其标准不确定度（u24）。

3.2.5 液体恒温槽内温度不均匀性引入的标准不确定度

根据《JJG207—92标准铂电阻温度计检定规程》的要求可知，液体恒温槽内温度均匀度≤0.02 ℃，即区间半宽度为0.02 ℃，按均匀分布，取包含因子，由式（4）可计算出其标准不确定度（u25）。

3.2.6 由数据处理终端的修约误差引入的标准不确定度

在校准时，温度输出值最终保留2位小数，则其修约误差最大为0.005 ℃，即区间半宽度为0.005 ℃，按均匀分布，取包含因子为由式（4）可计算出其标准不确定度（u26）。

3.2.7 由标准装置引入的标准不确定度

以上各分量的标准不确定度互不相关，且灵敏系数的绝对值为1，根据合成标准不确定度通用公式[3]（式5）可计算出由标准装置引入的合成标准不确定度（u2）。

式中：uc为合成标准不确定度；ui为输入分量的标准不确定度；n为输入分量个数。

3.3 合成标准不确定度

3.3.1 输入分量标准不确定度数据汇总

干湿球温度表在校准时其不确定度来源主要由干湿球温度表和标准装置两大类引入的，则这两大类各输入分量标准不确定度数据汇总（表2），这两大类的合成标准不确定度数据汇总（表3）。

表2 各输入分量标准不确定度数据汇总

表3 输入分量合成标准不确定度数据汇总

3.3.2 合成标准不确定度

在干湿球温度表校准过程中，由干湿球温度表引入的标准不确定度分量和由标准装置引入的标准不确定度分量是互不相关的，由式（5）可计算出干湿球温度表校准结果的合成标准不确定度（uc）：+30 ℃为0.021 ℃、0 ℃为0.021 ℃、-40 ℃为0.022 ℃。

3.4 扩展不确定度

在干湿球温度表校准过程中，取覆盖因子为2，扩展不确定度提供95%的置信水准，由扩展不确定度计算公式[3]（式6）可计算出干湿球温度表校准结果的扩展不确定度（U）：+30 ℃为0.05 ℃，0℃为0.05 ℃，-40℃为0.05 ℃。

式中：U为校准结果的扩展不确定度；uc为校准结果的合成标准不确定度；k为覆盖因子。

气象用玻璃液体温度表中其他类别的温度表可参考上述表确定其校准结果的扩展不确定度。

4 结论

本文采用GUM法对干湿球温度表的校准结果进行了不确定度分析与评定，并得出如下结论：

(1)干湿球温度表示值重复性和分辨力、二等标准铂电阻温度计固定点的稳定性和工作电流引起的自热效应、液体恒温槽内温度波动性和不均匀性、数据处理终端的修约误差都对校准结果的不确定度有着直接的影响；

(2)干湿球温度表分辨力、液体恒温槽内温度波动性与不均匀性分量对校准结果不确定度的影响较大，直流测温电桥分量对校准结果不确定度的影响可忽略不计，其余分量对校准结果不确定度的影响都比较小；

(3)为了减小恒温槽内温度波动性与不均匀性所引起的不确定度，可增加其稳定时间，或者将二等标准铂电阻温度计与被校准仪器尽量固定于液体恒温槽内的中央位置，且二者的感温部分尽可能处于同一水平面。以上不确定度来源分析与评定方法可供气象计量检定工作者及使用者参考。