智能电网中终端用户的双向能量交易算法

刘迪迪，孙浩天，肖佳文，JIANG Frank，郑鲲鲲

(1.广西师范大学 电子工程学院，广西壮族自治区 桂林 541004；2.广东澳鸿科技有限公司，广东 中山 528437)

智能电网将成为新一代的电网。与传统电网相比，其具有巨大变革性的特征，例如，可再生能源(太阳能或风能等)成为电网的一部分，终端用户，如家庭、社区或公司，收集可再生能量并将收集的能量存储在本地电池中，扮演微发电单元的角色[1]，智能电网赋予了供给者和消费者对资产和服务控制的权利，该环境下终端用户可以与电网进行双向能量交易[2-3]。此外，智能电网为平滑负荷，提高消纳能力，一般通过动态地调整电价来平衡电力消费者时变的负载[4-5]。智能电网中这些新特征，为终端用户提供了可通过与电网能量交易获得最大利益的机会。

文献[6-8]研究了不同网络的能量管理及传输调度问题。这些文献考虑的供电源均为固定电网，没有考虑和分析智能电网的新特征以及电价时变性带来的能量管理的新问题。文献[9-10]中作者提出了在智能电网时变电价下不同终端的动态能量管理方案，考虑终端基于时变电价从智能电网购买电量，从而最小化终端的电费成本，但没有研究终端出售能量给智能电网(即双向交易)的问题。文献[11]基于强化学习研究多个用户在不完全信息约束下能量交易的博弈问题，提出一种自适应学习算法来寻找多个用户之间的纳什均衡，但没有考虑用户和智能电网之间的能量交易以及能量管理问题。

笔者主要考虑智能电网中的终端用户，如配备有可再生能源收集装置和储能电池的家庭、小区或公司。允许终端用户与智能电网进行双向能量交易，用户基于电价的波动和用户当前的状态(当前能量收集和需求的状况及电池中的电量等)，在满足用户的即时能量需求的情况下，由能量管理单元(EMU)决策是否从电网购买能量存储在电池中，以备电价高而用户收集的能量不足时使用或出售给电网，从而使用户获益。此外，用户从可再生源收集的能量以及对能量的需求均具有高度不可预测性，因此加大了能量交易问题的随机性。基于李雅普诺夫理论，笔者提出了一种复杂度低的动态能量交易算法，在智能电网电价实时波动、终端用户的实时能量需求以及从可再生源收集能量的统计特性均未知的情况下，寻找终端用户长期平均效益最优算法，并分析电池容量大小对用户收益的影响。

1 建模和问题描述

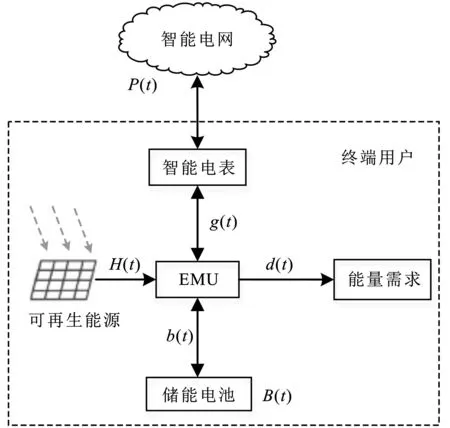
图1 终端用户与智能电网的能量 交易和管理模型模型

智能电网中终端用户的能量交易和管理模型如图1所示。终端用户与外部智能电网相连。智能电网的电价是时变的，在t时隙的价格记为P(t)，终端用户从可再生源收集能量，假设t时隙收集的能量记为H(t)，终端用户t时隙需求的能量记为d(t)。不同于文献[12]将收集的能量先存入电池再供用户使用，本模型将收集的能量直接供终端用户使用，若能量有剩余，即H(t)-d(t)>0，则由能量管理单元决策将剩余的能量存入电池或卖给智能电网，这样可减小储能电池的充/放电次数，提高电池的寿命。若t时隙终端用户收集的能量不能满足能量的需求，即H(t)-d(t)<0，则对于不足的部分，一部分从电池放电获取，其余的部分从外部智能电网获取。假设t时隙电池存入/释放的能量记为b(t)，用户与智能电网交易的能量记为g(t)，b(t)和g(t)的值均可为负值。假定b(t)>0表示电池放电，b(t)<0则表示电池充电，g(t)>0表示用户从智能电网购买能量，g(t)<0则表示用户出售能量给智能电网。

由模型可知，用户任意时隙能量供需的关系满足

d(t)=H(t)+g(t)+b(t)。

(1)

此外，允许电池从外部智能电网充电，直观地，当外部智能电网电价较低，充电电池从外部智能电网充电存储起来，供用户在电价高且收集能量不足的时候使用，可减少用户的能量成本。用bmax表示电池在每个时隙的最大充/放电速度；显然，任意时刻都满足|b(t)|≤bmax，这是物理硬件电路的制约。用B(t)表示t时隙始电池的电量，则电池的能量更新方程式为

B(t+1)=B(t)-b(t)。

(2)

若Bmax表示电池的最大容量，则有b(t)≤B(t)≤Bmax。

智能电表实现用户终端和智能电网之间的能量双向传递，由能量管理单元决策交易量g(t)的正负和大小。当g(t)>0时，终端用户从智能电网购买额外能量的价格为P(t)；当g(t)<0时，终端用户出售能量给智能电网的价格为βP(t)，其中β为(0，1)区间的常数，参数0<β<1的原因是智能电网从终端用户汲取能量进行传输管理，必然存在能量损耗，比如AC/DC转化带来的能量损耗以及传输线路带来的能量损耗等。因此，当终端用户从智能电网获取能量，则花费的成本为

P(t)(g(t))+=P(t)(d(t)-H(t)-b(t))+，

(3)

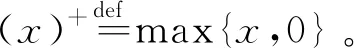
βP(t)(g(t))-=βP(t)(d(t)-H(t)-b(t))-，

(4)

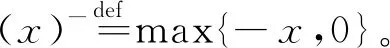
2 问题规划及求解

终端用户每时隙收集的能量H(t)和需求的能量d(t)均为随机过程，同时智能电网中的电价P(t)是时变的，终端用户的能量管理单元基于当前时隙的这些变量(P(t)，H(t)，d(t))，并根据当前电池中存储的电量B(t)，决策当前时隙对电池充电还是放电，即b(t)，以及决策从外部电网购买能量还是出售能量给外部电网，即g(t)；两者受到式(1)约束，因此文中问题规划中只需对b(t)进行决策。文中的优化目标是最大化终端用户能量交易的长期平均效益，该问题规划如下：

(5)

其中，式(5)为优化目标，将终端用户t时隙的收益减去成本；E[·]为期望，目的是寻找一种优化算法控制序列{b(t)}，使终端用户长期的收益达到最优。

2.1 李雅普诺夫优化

下面用李雅普诺夫理论方法对以上问题求解。首先构造一个衡量电池充、放电转换的变量X(t)：

X(t)=B(t)-VPmax-bmax，

(8)

其中，Pmax为所有时隙内智能电网的最高电价，V是控制参数。通过合理调节参数V来控制变量X(t)，以确保电池中的电量水平保持在合理范围内，即满足电池中电量状态约束式(7)。根据式(8)，X(t)的更新方程为

X(t+1)=X(t)-b(t)。

(9)

ΔL(X(t))=E{L(X(t+1))-L(X(t))|X(t)}，

(10)

其中，

(11)

(12)

最小化每个时隙的李雅普诺夫漂移，则能保证满足约束式(7)。笔者的目标是在满足约束式(6)、(7)和式(1)、(2)的基础上最大化目标函数式(5)，再根据李雅普诺夫漂移加惩罚优化方法，最大化目标函数式(5)等价于最小化李雅普诺夫“漂移加惩罚”函数，因此问题的求解可转化为

min：ΔL(X(t))-VE[βP(t)(g(t))--P(t)(g(t))+]，

(13)

这里的新目标函数式(13)的界限如下：

ΔL(X(t))-VE[βP(t)(g(t))--P(t)(g(t))+]≤

(14)

因此最小化式(13)转化为最小化不等式(14)的右边项问题，利用李雅普诺夫优化方法，最小化不等式(14)右边项的每个时隙，整理并去掉决策变量b(t)的无关项，得到

(15)

式(15)中，第1项整理得到

X(t)b(t)=X(t)[(d(t)-H(t)-b(t))-(d(t)-H(t))]=

X(t)[(d(t)-H(t)-b(t))+-(d(t)-H(t)-b(t))--(d(t)-H(t))]。

(16)

将式(16)代入式(15)，合并同类项并去除b(t)的无关项，转化为式(17)：

(17)

2.2 双向能量交易的动态算法

第1步 观察t时隙系统状态d(t)、H(t)和P(t)，根据式(8)求出X(t)。

第2步 最小化式(17)，决策出最优的b*(t)，方法如下。

因为0<β<1，可知X(t)+VP(t)>X(t)+VβP(t)。在约束条件式(1)、(2)和式(6)的约束下，最小化式(17)，得到终端用户在t时隙的决策。

① 若X(t)+VβP(t)≥0时，则此时的决策为b*(t)=bmax，即B(t)-bmax≥V(Pmax-βP(t))，表明电池中的电量较多，或者智能电网的电价较高，此时电池尽可能地放电。

② 若X(t)+VP(t)≤0，则此时的决策为b*(t)=-min(bmax，Bmax-B(t))，即B(t)-bmax≤V(Pmax-P(t))，表明电池中的电量较少，或者智能电网的电价较低，此时电池尽可能地充电。

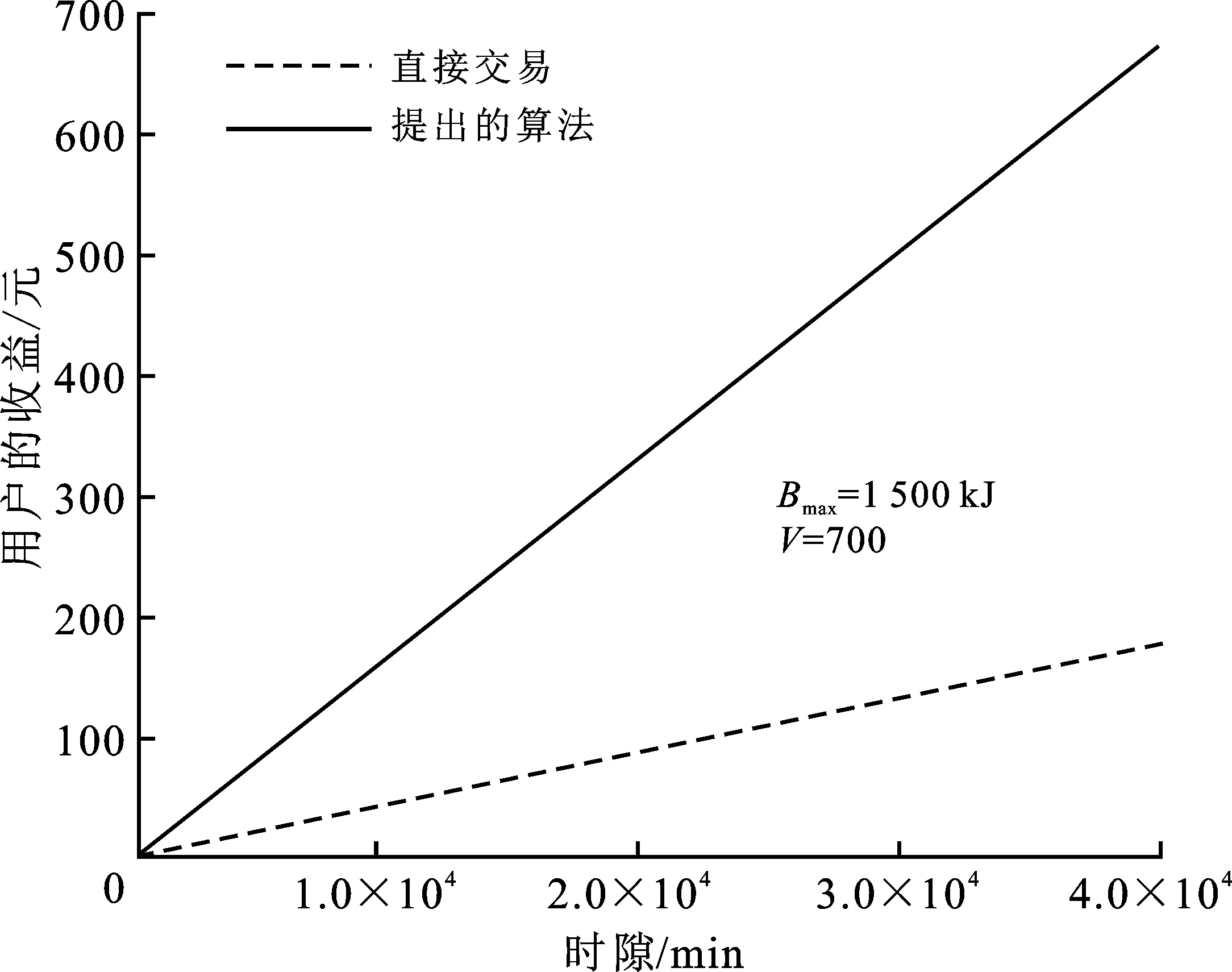
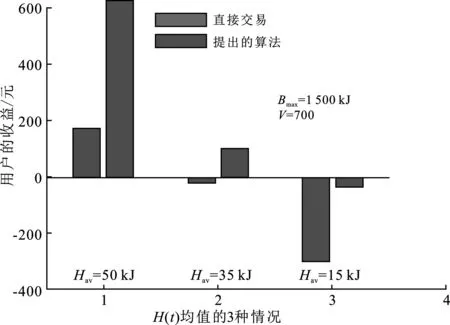
③ 若X(t)+VP(t)>0>X(t)+VβP(t)，即V(Pmax-P(t))

若H(t)≤d(t)，则b*(t)=min(bmax，d(t)-H(t))；否则b*(t)=-min(bmax，min(Bmax-B(t)，H(t)-d(t)))。

第3步 确定终端用户与外部智能电网之间的能量交易量g(t)。确定b(t)后，g(t)=d(t)-b*(t)-H(t)。

若g(t)>0，则终端用户从外部电网购买能量，花费的成本为P(t)g(t)；否则，终端用户出售能量给外部电网，此时终端用户产生收益为-βP(t)g(t)。

第4步 分别根据式(2)和(9)更新电池电量B(t+1)和构造的变量X(t+1)。

终端用户与智能电网长期(T→∞)交易，终端用户在t(t为任意值)时隙的决策仅需要观察该时隙系统状态d(t)、H(t)和P(t)，求出X(t)，即可获得决策结果b(t)和g(t)，从而得到用户该时隙的收益，用户的累计收益(或平均收益)仅随时隙个数T呈线性增加，可见所提算法的复杂度低，且不需要能量需求、电价变化和能量收集过程的先验知识。

2.3 算法性能分析

定理1在时隙t∈{0，1，2，…，T-1}上任意常数V满足0≤V≤Vmax，Vmax可表示为

(18)

其中，Pmax为最大电价值，Pmin为最小电价值。则上述算法有以下性质：

(1)X(t)在所有时隙都有界，即

-VPmax-bmax≤X(t)≤Bmax-VPmax-bmax。

(19)

(2) 如果P(t)，H(t)，d(t)在时隙上独立同分布，则在上述算法下的平均成本的期望与最优解的差不超过C1/V，即

(20)

其中，Copt为总收益的时间平均的最优值，C1=bmax/2。

从定理1可知，目标函数(用户收益)随参数V的增大无限趋于最优值Copt，但同时要考虑将充电电池中的实时电量控制在合理的范围，其最大值一般不超过式(18)，因此需合理调节V的值。

3 仿真结果

由前面的分析可知，提出的算法不受随机过程概率分布的影响。为方便演示仿真结果，假设用户能量收集和能量需求过程分别服从不同分布，智能电网的电价根据一天中不同时段的负荷大小而变化，一天中有两个电价高峰，电价在0.5元至2.0元之间波动。时隙间隔取 1 min，一天共划分为1 440个时隙，假设考虑一个月30天的情况(43 200个时隙)，电价每天的变化趋势均重复第一天电价模型。考虑普通家庭用户平均每月用电量为360度，并参考市场上充电电池的容量范围，具体参数设置见表1。

表1 参数设置

首先，为验证提出的实时能量交易算法的有效性，将提出的算法与直接和智能电网进行能量交易的情况(简称直接交易)进行对比，直接交易是指用户不存储能量，若收集的能量不能满足能量需求，不管此时电价高低，直接从智能电网购买不足的部分；反之，若收集的能量有剩余，不管此时电价高低，都出售给智能电网。两种算法下终端用户30天累积收益对比如图2所示。此时电池的最大容量Bmax=1 500 kJ，基于V的计算公式，选取V=700。从图2可看出，提出的算法明显优于直接与电网交易，在30天末，用户直接与电网交易的收益为181.9元，基于提出的算法，用户的收益为677.5元，平均每月多收益495.6元。

图2是在能量收集均值大于用户能量需求均值情况下的收益，即每时隙能量收集均值Hav=45 kJ，能量需求dav=30 kJ。保持能量需求不变，图3给出了3种能量收集均值下用户30天末的收益直方图，即Hav分别为50 kJ、35 kJ、15 kJ的三种情况。从图3中可以看出：① 收集的能量平均值越大，可用的免费能量越多，用户收益越高；② 收集的能量均值小于用户能量需求均值，则用户需要从智能电网购买额外能量以满足需求，用户的收益为负，即用户的成本，可见基于提出的算法用户成本低于直接与电网交易的成本，如图3中的情况3；③ 在每种能量收集均值情况下，基于提出的算法都优于直接与电网交易的收益。

图2 两种算法下终端用户30天累积收益对比

图3 3种能量收集均值下用户30天末的收益直方图

为评估电池容量Bmax对所提算法的影响，图4给出了在不同电池容量下用户的收益。图中针对不同的Bmax，选取了合理的调节参数V。从图4可以看出，电池越大，用户的收益越高。这是因为电池容量越大时，则能存储更多剩余的收集的能量，或存储更多来自智能电网的低电价能量，以备电价高且用户能量需求较少时出售给智能电网，从而增大收益；或者在电价高且用户收集的能量不足时供用户使用，从而节约成本。但用户的收益并不随着电池容量增大而线性地增大，这是因为电池最大充/放电速率bmax有限，即使电池容量很大，但单位时间内电池无法存入或出售更多的能量。此外，电池的容量越大，电池成本越高，因而用户选取电池容量时应根据电池成本和带来的效益折中选择。

图4 不同电池容量吐下基于所提算法用户的收

图5 用户的总收益(30天末)随参数V值变化

图6 电池在不同V值下的实时能量(第10天)

文中设置的控制参数V，目的是通过合理调节参数V来确保提出的算法使电池中的能量B(t)保持在合理范围内，即保证0

4 结束语

笔者主要研究配备能量收集和能量存储装置的终端用户与智能电网间的能量交易和管理问题。在构建模型时充分考虑如何减少电池充放电次数，以延长储能电池寿命；在智能电网电价实时波动、终端用户的实时能量需求以及从可再生源收集能量的统计特性均未知的情况下，基于李雅普诺夫优化提出了一种复杂度低的动态能量交易和管理算法。理论证明，该算法可使终端用户的长期平均效益无限接近到最优值。并通过仿真验证了该算法的有效性。仿真结果表明，所提算法在不同参数设置下都具有较好的性能；终端用户基于所提算法比直接交易能获得更多收益。并分析了电池容量大小对用户收益的影响，为用户选择电池容量给予了理论指导。