基于模糊确信可靠度的城轨列车齿轮轻量化设计方法
庞其城, 杨建伟, 李 政
(1.北京建筑大学 机电与车辆工程学院, 北京 100044;2.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室, 北京 100044)
轻量化这一概念最早源自汽车制造行业,汽车的质量减轻,可以带来更良好的操控性和加速性[1]。随着“节能、减排”等环保理念深入人心,轻量化的概念开始在各行各业中展开。其在工程中的主要思想为:在确保稳定提升性能的基础上,节能化设计各零部件[2]。随着城市轨道交通的快速发展,对于城轨车辆的技术指标要求越来越高,要在保证车辆运行安全可靠的情况下,做到节约能源、降低成本、减轻重量等,轻量化成为车辆设计中必不可少的环节之一。目前城轨车辆主要的轻量化设计方向分为2类[3]:第一类为材料轻量化设计,指在车体、牵引系统、制动系统、空调系统和转向架等车辆重要的子系统中使用既满足强度要求,又可实现轻量化目的的新型材料;第二类为结构轻量化设计,通过理论校核或有限元仿真计算、设计出更合理的结构、减少零部件冗余设计等途径实现轻量化。
城轨列车各个子系统中,牵引系统中的零部件质量占用了车辆总体质量中很大一部分,其中齿轮箱中的大量传动齿轮由于采用比较保守的设计思路,造成了一部分零部件可靠性功能冗余,不仅使整车的质量增加,占用车底大量空间,而且提高了制造成本。采用轻量化设计优化可以极大改善以上问题。但对于齿轮箱中传动齿轮来说,材料轻量化设计需要在材料领域有所突破,以目前现有技术实现难度较大。而在结构轻量化设计方面,通过合理优化齿轮的结构就可以相对简单地实现齿轮轻量化。
本文在对城轨车辆齿轮箱中齿轮的弯曲疲劳可靠性预测相关研究的基础上,建立基于齿轮弯曲疲劳的性能裕量模型。在故障数据样本较少、存在认知不确定性对可靠性预测结果影响较大的情况下,运用确信可靠度评估方法,对某型城轨车辆齿轮箱中的齿轮齿根弯曲疲劳强度进行可靠性预测,计算出在满足列车运行安全的条件下所需达到的最低参数要求,并在尽量便于修改的情况下,对现有齿轮箱中传动齿轮的齿宽进行优化,以达到齿轮的轻量化设计。
1 确信可靠度分析基本理论
1.1 性能裕量理论
性能裕量(Performance Margin, PM)[4]指性能参数与其性能失效阈值之间的差距,性能裕量可用于表征系统的失效。性能裕量在确信可靠度模型中起着重要作用,假设将p称为性能参数,pth称为性能失效阈值,当性能参数p达到性能失效阀值pth时,系统发生故障。在大多数情况下,存在2类性能参数模型的失效情况[5]:
1) 当p≥pth时系统失效,此模型为望小情况(STB)。
2) 当p≤pth时系统失效,此模型为望大情况(GTB)。
根据上述情况,性能裕量M模型可以表示为:
(1)
性能裕量描述了性能参数与其阈值之间的差距,当M<0时,故障发生。在实际情况中,经常受到偶然性和认知不确定性的影响。所以在前期的零部件设计过程中,预留的性能裕量越大,系统或零部件发生故障的可能性越低,随之可靠性越强。因此,将性能裕量作为一个不确定的随机变量进行建模,得到了性能裕量意义下的可靠性的定义[5]。
1.2 轻量化设计分析框架
轻量化设计的计算具体流程如图1所示。

图1 轻量化设计计算流程Fig.1 Lightweight design calculation process
2 运营工况下齿轮确信可靠度模型的建立
影响齿轮可靠性的主要原因为齿轮齿根在纵向载荷上受到齿根弯曲应力而发生弯曲疲劳断裂,所以为了深入研究齿轮可靠性相关问题,应建立齿轮齿根弯曲疲劳可靠性模型。
在运营工况下所获得的传动齿轮故障数据有限,无法满足大数定律。在复杂的工况下运行时,系统存在较大的不确定性,使用基于传统贝叶斯可靠性的评估方法导致计算结果偏差较大。本文使用确信可靠度评价方法。主要优势是考虑复杂环境下认知不确定情况对可靠性结果的影响,运用公理化的数学方法对模型的确信可靠度进行更加准确的评估,使得最后轻量化结果更加准确可信。
2.1 基于确信可靠度的齿轮可靠性模型建立
选用的试验齿轮为某型城轨车齿轮箱中传动齿轮,材料为18CrNiMo7-6,其化学成分及占比见表1。试验齿轮参数见表2,齿轮做渗碳淬火热处理,有效硬化深度1.00~1.50 mm,齿面硬度58HRC-62HRC,芯部硬度≥30 HRC。

表1 18CrNiMo7-6材料化学成分及占比

表2 试验齿轮参数
参考文献[6]中齿轮箱中齿轮齿根应力确定方式,依照GB/T 3480—1997《渐开线圆柱齿轮承载能力计算方法》[7]中的齿根应力计算公式计算齿轮齿根弯曲应力σF和弯曲许用应力σFP:
(2)
式中:YFE为载荷作用于E点时的齿形系数,根据试验齿轮参数,取值2.25;YSE为载荷作用于E点时的应力修正系数,取值1.77;YST为齿轮的应力修正系数,取值1;YδγlT为相对齿根圆角敏感系数,取值1;YRrelT为相对齿根表面状况系数,取值1;YX为计算弯曲强度的尺寸系数,取值1;Ft为端面内分度圆周上的名义切应力,N;b为齿宽,mm;m为齿轮模数。
σFP=YNTYSTYXYδγlTYRrelTσFlim
(3)
式中:YNT为齿轮弯曲疲劳寿命系数,取值1;σFlim为齿根弯曲疲劳极限。
试验选用的齿轮与文献[8]中物理特性相似,故引用其齿轮齿根弯曲疲劳极限,设随机正态分布σFlim~N(μ=679,σ2=852)。
在城轨列车齿轮箱中传动齿轮的齿根弯曲疲劳确信可靠度计算模型中,选取齿轮齿根弯曲应力σF作为性能参数p,选取齿轮齿根弯曲许用应力σFP作为性能失效阈值pth。当齿轮齿根弯曲应力σF大于齿轮齿根弯曲许用应力σFP时(即p>pth),系统失效,判断此确信可靠度模型的失效类型为望小。本试验中,齿轮齿根弯曲许用应力σFP的值受单一参数齿根弯曲疲劳极限σFlim影响,所以性能失效阈值pth是随机变量且服从概率分布ψ(x)。齿轮齿根弯曲应力σF受切应力Ft影响,为方便计算,将2个参数分别进行考虑,故p是不确定变量且服从不确定分布φ(x)。
根据文献[8]中的确信可靠度模型计算公式,当p是不确定变量且服从不确定分布φ(x),pth是随机变量且服从概率分布ψ(x),并且系统的失效模型属于望小情况,此模型的确信可靠度RB计算公式为:

(4)
即:

(5)
ψ′(x)是σFlim~N的概率密度函数,可表示为[4]:
(6)
式中:μ为均值,σ为标准差。
2.2 运营工况下齿轮模型确信可靠度计算
根据城轨列车实际运营工况,在列车处于牵引工况时,由于电机的牵引作用,使得传动齿轮所受的载荷变化较大,容易产生可靠性方面问题,故主要考虑在牵引状态下齿轮箱中传动齿轮所承受的载荷情况,根据列车牵引电机的机械特性,将驱动转矩分为恒转矩区和恒功率区,以满足牵引的需要[9]。因此,电机驱动力矩可以表示为:
(7)
式中:Te为额定转矩,N·m;Pe为额定功率,W;n为电机转速,r/min;ns为同步转速,r/min。
根据试验模拟牵引工况得出驱动电机的工作特性,绘制电机驱动转矩曲线如图2所示[10]。
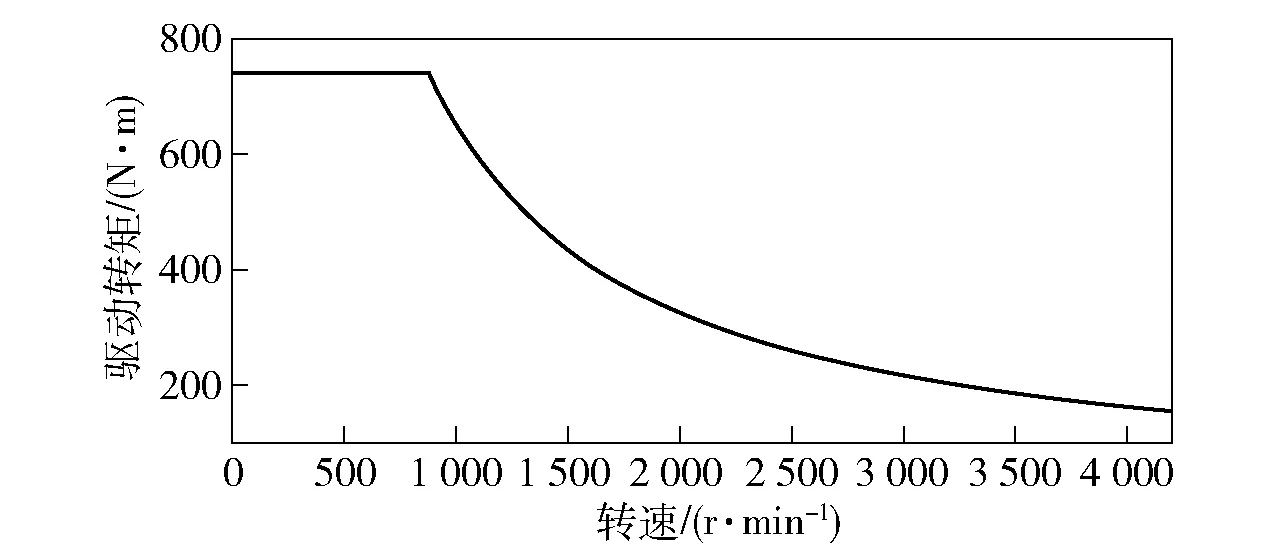
图2 电机牵引条件下的驱动转矩曲线Fig.2 Drive torque curve under motor traction
牵引电机输出的转矩直接传递给齿轮箱中的传动齿轮,可以将分度圆上的切应力Ft表示为[11]:
(8)
式中:d为齿轮分度圆上的直径,mm,齿轮分度圆半径等于齿轮模数与齿数的乘积,即d=mz。
由式(8)可以看出,当驱动转矩处于恒转矩区时,传动齿轮分度圆上的切应力Ft为定值不变;当驱动转矩处于恒功率区时,分度圆切应力随转速的增大单调减小,呈反比例函数,根据不确定概率运算法则[9]可以求出p的不确定分布的解析解为:
(9)
齿轮分度圆所受的最小切应力Fa≈2 727 N,最大切应力Fb≈13 273 N,故设齿轮齿根所受的切应力可表示Ft~N(Fa=2 727,Fb=13 273)。
根据式(5)计算出在参数Ft的不确定性影响时的确信可靠度RB=0.999 4。
2.3 参数敏感度分析
在弯曲疲劳极限σFlim不变的情况下,通过改变齿轮分度圆上所受的切应力Ft~N(Fa=2 727,Fb=13 273)中最小切应力Fa和最大切应力Fb的值,使2个参数在给定的区间内变化,得到模型的可靠度RB随参数Ft中变量Fa、Fb的三维变化趋势,如图3所示。之后通过改变Fa、Fb中某个变量在给定的区间内变化,另一变量保持原有数值不变,得到可靠度RB随参数Ft中单一变量的变化曲线如图4所示。
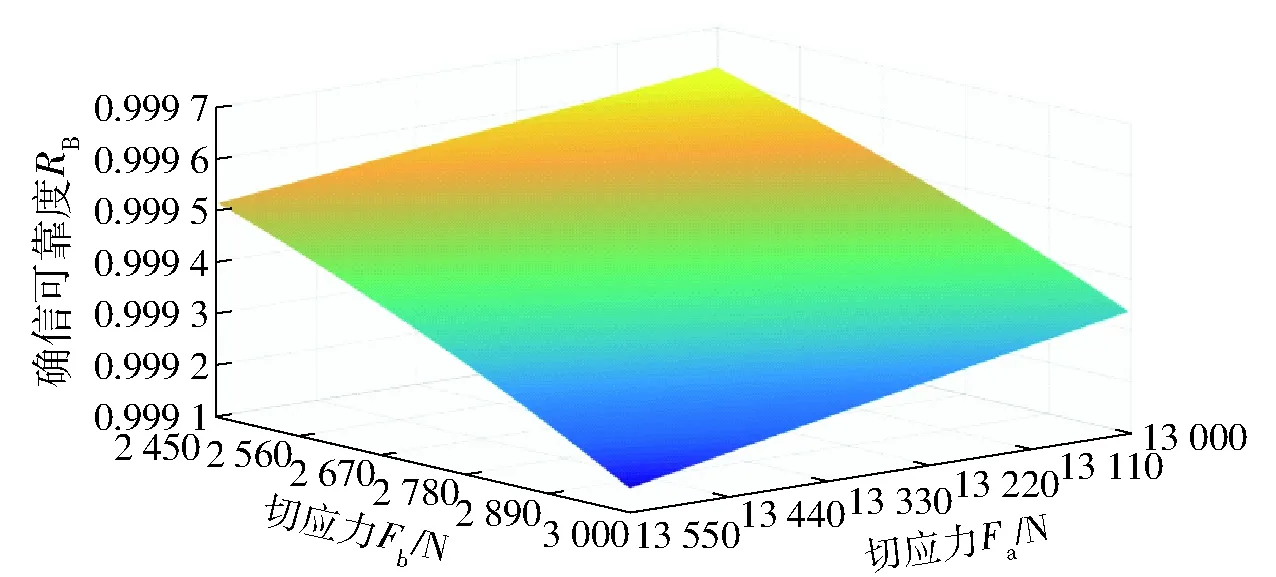
图3 可靠度RB与参数Ft中变量的关系Fig.3 Relationship between reliability RB and variables in parameter Ft

图4 可靠度RB随参数Ft中单一变量的变化曲线Fig.4 Variation curve of reliability RB with a single variable in parameter Ft
从图3中可以看出随参数Ft中Fa、Fb数值增大,即参数Ft的不确定性增大时,系统的确信可靠度呈现逐渐降低的趋势;对于图4,当参数Fa、Fb增大时,确信可靠度呈现近似线性的减小,且最大切应力Fb的改变对模型的确信可靠度RB影响较大,而RB在Fa的值域中变化范围较小。
在分度圆切应力Ft和齿形系数YFE不变的情况下,通过改变弯曲疲劳极限σFlim~N(μ=679,σ2=852)中均值μ和标准差σ的值,使2个参数在给定的区间内变化,得到模型的可靠度RB随参数σFlim~N中变量μ、σ的三维变化趋势,如图5所示。之后通过改变参数μ、σ中某个变量在给定的区间内变化,另一变量保持原有数值不变,得到可靠度RB随参数σFlim~N中单一变量的变化曲线,如图6所示。

图5 可靠度RB与参数σFlim中变量μ和σ的关系Fig.5 Relationship between reliability RB and variables μ and σ in parameter σFlim
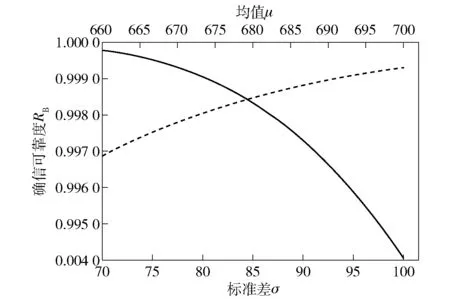
图6 可靠度RB随参数σFlim中单一变量的变化曲线Fig.6 Variation curve of reliability RB with a single variable in parameter σFlim
图5中可以看出,随参数YFE中μ、σ数值的增大,系统的确信可靠度呈现逐渐降低的趋势,但标准差σ的变化较大。对于图6,当均值μ逐渐增大时,可靠度RB的值随着μ的增大而增大,且增长速率逐渐降低。相反,确信可靠度RB的值随着标准差σ的增大而减小,增长速率逐渐加快。将2条线的趋势进行比较,标准差σ数值变化对结果确信可靠度RB的影响更显著。
3 齿轮轻量化设计相关分析及计算
通过建立齿轮齿根弯曲疲劳强度性能裕量模型,计算出了在牵引工况下,原齿轮受Ft不确定性影响,齿轮齿根弯曲疲劳的确信可靠度RB趋近于1。但是对于齿轮箱系统而言,此部分可靠性设计过高,导致可靠性功能冗余,可适当降低可靠性以换取齿轮的轻量化。
在齿轮相关的轻量化设计中,结合现有的实际情况,较难在齿轮的材料上发生较大的技术突破,无法通过材料轻量化的设计方法实现目标。而结构轻量化设计方法相对简单易行,原齿轮在设计过程中过分地注重安全性和耐用性,设计思路相对保守,导致齿轮在设计上使用大量冗余设计以确保其可靠性。因此通过结构轻量化相关计算,减小原齿轮中部分结构参数可实现轻量化的目的。
3.1 齿轮齿宽参数模糊化
关于齿轮结构轻量化设计方法有很多种,在齿轮传动系统轻量化过程中,支撑跨距、齿轮直径、齿数、模数等参数的优化,都可以实现齿轮轻量化。但是以上的轻量化方法对于齿轮及齿轮组设计修改幅度较大,需要对齿轮箱整体系统重新设计,增加了轻量化的成本和制造难度。为了尽量不改变原齿轮箱及齿轮组结构,只替换相关齿轮即可实现轻量化,对齿轮齿宽参数进行优化是相对简单有效的方法。
在设计齿轮齿宽时,应满足相应规格的标准齿宽系数,齿宽系数φa用于表示齿宽的相对值,如:
(10)
式中:a为中心距,mm;b为齿宽,mm。
使用的齿轮箱中的齿轮齿宽设计根据文献[12]中规定,应满足开式齿轮齿宽系数φa=0.1~0.3。由于原齿轮设计中采用的是相对保守的设计思路,所以选择的齿宽系数φa数值较大,即齿宽的参数设计较大。为了证明所取齿轮齿宽参数在一个较小的范围内时仍能保证系统的可靠性,运用模糊理论将齿轮齿宽参数模糊化。由于所用的齿轮齿宽轻量化模型考虑了大量在小样本数据下存在的不确定性影响,在齿宽参数模糊化模型建立的过程中更适用于三角模糊数,且三角模糊数更适用于解决质量管理、决策与模糊规划的一类模型。故定义齿宽参数为三角模糊数,建立一般类系统部件的模型隶属函数[13]:
(11)
式中:a、m、b分别为某一模糊变量的最小可能值、最可能值和最大可能值,(a,m,b)构成三角模糊数,其图形表达如图7所示。

图7 三角模糊数的隶属函数Fig.7 Membership function of triangular fuzzy numbers
本文主要解决齿轮的轻量化问题,为了减少不必要的计算,只需考虑模糊集中小于等于最可能值的情况,即x≤m时。构造关于齿轮齿宽的模糊集可表示为b=(1.00~10.00)mm。
3.2 利用确信可靠度的轻量化计算
将得出的齿轮齿宽模糊集代入式(5)中,将计算得出结果绘制成如图8所示的齿宽的模糊确信可靠度曲线。

图8 齿宽的模糊确信可靠度曲线Fig.8 Fuzzy belief reliability curve of tooth width
根据图8可以看出确信可靠度RB随着齿宽b的逐渐增加而增加,但增长趋势逐渐放缓最后在齿宽10.00 mm时逐渐趋近于1,说明齿宽越宽齿轮的可靠性越高。但是过高的可靠度对于整个齿轮箱系统而言,此部分的可靠性功能超出了系统整体的预期寿命[14],所以可适当减小齿宽以换取齿轮的轻量化。
以RB=0.950 0为预期的可靠度期望,模糊确信可靠度参数计算的结果所得见表3,此时的齿宽b≈6.56 mm,同时为了满足工业化制造加工需求,齿宽取整数7.00 mm,此时的确信可靠度RB=0.967 1,符合本系统的预期可靠度期望,并且符合轻量化的目的。

表3 模糊确信可靠度参数
4 结论
本文利用确信可靠度评估方法对齿轮的可靠性进行评估。引入性能裕量参数指标,建立基于齿轮弯曲疲劳的性能裕量模型。对某型城轨车齿轮箱中齿轮齿根弯曲疲劳强度进行可靠性预测,计算出列车在运行的工况条件下齿轮齿根弯曲疲劳强度的确信可靠度,并对其可行的轻量化设计方法进行分析,在便于修改的情况下,对现有齿轮箱中传动齿轮的齿宽进行优化。同时引入模糊理论,计算得出齿宽的模糊确信可靠度曲线,计算出符合设计预期的齿轮齿宽参数,实现齿轮的轻量化设计。
计算结果表明,当齿宽缩减为7.00 mm时,齿轮箱系统在保证基本可靠性功能的情况下,齿轮的体积和质量减少了约30%。
研究对齿轮的轻量化设计提供了一种新的设计思路,不仅节约了部分车底宝贵的空间,降低了齿轮的制造成本,减少钢铁资源的浪费,并且可以以此为例推广到更多的轻量化设计工程中,具有较强的实用价值。

