逆变点焊电源的恒流控制技术

安徽理工大学电气与信息工程学院 姚威威

近年来，随着电力电子和计算机技术的快速发展，点焊机被广泛应用于机械、电气、航空航天、材料等领域。但在焊接的过程中都存在一些普遍的问题，例如，焊接电阻随时间非线性变化，焊接电流、电极压力、焊接时间等多种因素之间相互耦合。因此，建立逆变点焊电源控制系统的精确数学模型是十分困难的，仅依赖传统的PID控制满足不了实际焊接的效果。对于点焊机系统而言，影响焊接质量的最重要的因素是焊接电流，寻找合适的控制算法去保持焊接电流的恒定是非常必要的。

随着智能控制算法的不断涌现，模糊控制和人工神经网络控制的出现为解决这一难题提供了有利条件。他们不依赖于被控系统的数学模型，能有效处理非线性、强耦合时变、滞后的问题。模糊神经网络控制（FNNC）融合了模糊系统的语言推理能力和神经网络的学习机制的优点，在焊接过程中，通过对PI控制器的参数进行实时调整，使PWM波的占空比发生改变，从而维持焊接电流的恒定。

1 基于FNNC的逆变点焊电源恒流控制

逆变点焊电源的主电路和控制电路组成如图1所示，主电路涉及到的电能变换方式包括整流-逆变-整流。其工作过程如下：三相桥式整流电路将交流电整流成带有少许纹波的直流电，再经电容滤除纹波后作为全桥逆变器的母线电压，幅值在570V左右。中频变压器对逆变器的输出电压进行降压处理，得到幅值为10V以下的交流电，变压器的次级电压再经单相整流电路整流，最终给负载提供稳定的直流电。

图1 逆变点焊电源的恒流控制框图

焊接电流恒流控制的原理是：采样变压器二次侧实际输出电流，并与预先设定的焊接电流进行比较，二者的差值以及差值的微分作为FNNC的两个输入，FNNC经过模糊推理和神经网络的自学习等一系列运算过程，输出PI控制器的比例系数和积分系数的变化量，实时对PI控制器的参数进行调节，其参数计算公式如(1)所示。这样有效地改变了传统PI控制中，PI控制器参数无法在线整定的缺点。PI控制器的输出作为PWM波的占空比，用来控制逆变器开关器件的导通和关断时间。在焊接过程中，当负载电阻变化时，能维持焊接电流的恒定，这一措施在很大程度上提高了焊接质量。

2 模糊神经网络控制器

2.1 模糊神经网络的模型

在点焊机的控制系统中，为了提高焊接电流的精密性和稳定性，并结合所采样的焊接电流的特点，模糊控制中的清晰化、模糊推理以及清晰化等步骤由BP神经网络来实现。模糊神经网络的两个输入节点是经过量化因子处理过的焊接电流偏差以及偏差的变化率，整个网络中的神经元节点都与模糊控制有着密切的联系，网络从输入层到输出层的五层计算完成了模糊推理的所有过程，如图2所示。

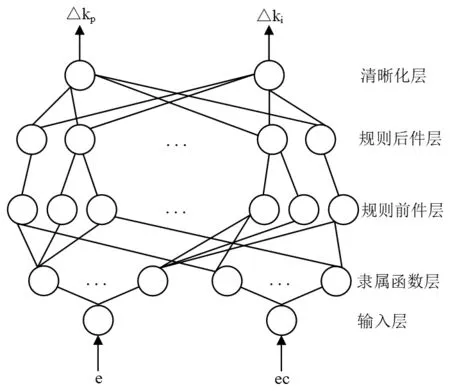
图2 模糊神经网络的模型

五层BP神经网络的每一层都有着明确的含义，netjp代表第p层第j个神经元的净输入，代表第p层第j个神经元的输出。

第一层是输入层，输入量e和ec与该层的两个神经元节点的连接权值都为1，则有：

第二层是隶属函数层，执行的功能是对上一层输入变量的精确值进行模糊处理。根据实际控制的需求，e和ec均定义了7个模糊子集，即为NL（负大）、NM（负中）、NS（负小）、Z（零）、PS（正小）、PM（正中）、PL（正大）。因此，该层有14个节点。一般，隶属函数选取三角型或者高斯型，为了简化运算，这里选取后者。

其中，mij、δij分别表示第i个输入变量的第j个模糊集合的高斯型隶属函数的平均值和标准差。i=1，2，j=1，2…7。

第三层和第四层共同构成规则层，由于e和ec各有七个模糊子集，因此，模糊规则共有49条。其中，规则前件层决定执行49条规则中的哪一条或者哪几条规则，也就是判断哪些规则被激活。后件层是对被激活的规则进行运算，构成系统总的模糊规则。例如，在一个采样周期中，被激活的k条规则分别为R1，R2…Rk，如果选取“或”运算，则总的模糊规则可以用公式(4)表示。

最后一层是清晰化层，将模糊量转换成能够对PWM占空比进行控制的精确量。

2.2 模糊神经网络的学习方法

神经网络的自学习过程就是不断调节各层网络之间连接权值的过程，通过不断调节，建立输入和输出之间的清晰、明确关系。依据Delta学习规则，当焊接电流的实际输出值和给定电流不同时，认为网络的误差是存在的，误差可以表示为：

通过网络层之间的推理计算，可以得出误差E是连接权值wrs（神经网络第r层和第s层之间的连接权值）的函数，由于训练的目的是让电流误差越来越小，逐渐逼近于设定，因此要求得误差函数的极小值，往梯度下降方向进行调整，即：

3 仿真结果

利用Matlab的Simulink的仿真工具，搭建了模糊神经网络PI控制下的焊接系统模型，当给定焊接电流为6kA时，焊接电流实际输出波形如图3所示。从波形可以看出，在电流上升阶段的动态响应横跨，在0.025s左右达到稳态，稳态阶段的电流基本能跟随给定，波形波动很小。

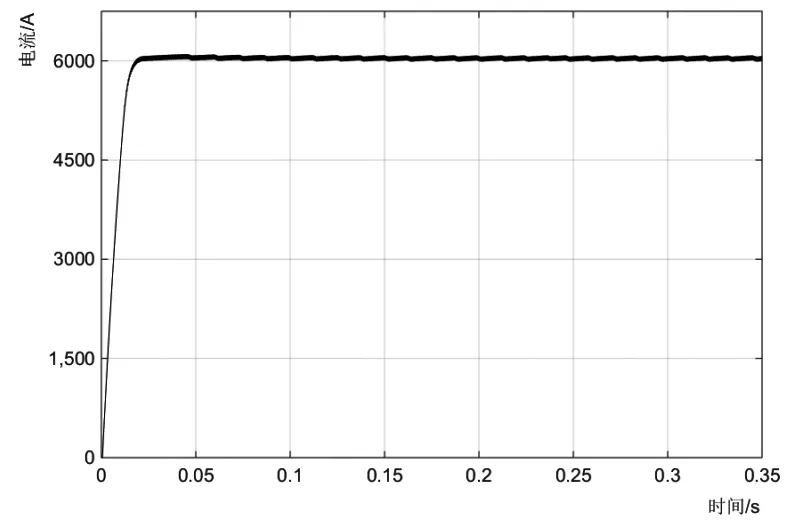
图3 焊接电流波形

结论：本文设计的基于模糊神经网络PI的电流控制方法，通过对PI控制器的参数实时在线整定，从而解决了焊接过程中负载电阻变化导致的焊接电流不稳定的问题。仿真结果表明，利用模糊神经网络控制能够提高焊接电流的快速性和稳定性，在很大程度上提高了焊接质量，具有一定的实际应用价值。