考虑桩——土相互作用的多跨连续梁桥梁自振响应分析

周小东 邹慧娜

1.江西省吉安市公路局吉安分局，中国·江西 吉安 343100

2.江西方兴科技有限公司，中国·江西 南昌 330025

1 引言

桥梁的动力特性是其结构自身的属性，反映了结构在动力作用下的反应特性[1]，分析和认识长跨径公路桥梁结构的自振特性及动力响应对桥梁的抗震设计具有重要的意义。自19世纪中期以来，中国对桥梁振动问题已进行了大量研究[2]。

张巍[3]以某新建三跨预应力混凝土变截面连续箱梁桥为背景，通过建立有限元仿真计算模型和动载试验现场测试相结合的方法对桥跨进行自振特性和动力响应分析，得出桥面平整度和车辆紧急制动对桥跨的冲击效应影响较大。

王岩[4]通过建立主跨220m连续刚构桥与矮塔斜拉桥地震动力分析模型，分析并比较了地震荷载作用对不同桥型的自振周期及对桥墩底部的内力影响。

曾勇、钟华栋等[5]利用MIDAS Civil建立不同腹板曲线连续刚构桥计算模型，通过改变桩基边界约束和激励角度，对比分析其自振特性和抗震性能变化规律。

苗战涛[6]以朝阳沟水库特大桥为研究对象，建立全桥空间力学有限元模型，通过计算多箱室波形钢腹板箱梁、传统砼腹板箱梁的自振频率和振型，对比分析了两种截面形式的动力特性。

马驰、刘世忠等[7]通过考虑剪滞剪切变形效应和顶底板的不同材料属性，采用等效刚度法对传统波形钢腹板（简称CSW）和CSWSB组合箱梁的动力特性进行对比，分析得到CSW组合箱梁的自振频率均小于CSWSB组合箱梁的自振频率，振型模态完全吻合，振动趋势一致。

成凯、叶锡钧等[8]通过有限元分析软件MIDAS对某大跨度异形人行拱桥动力特性进行分析，分析了拱桥的自振频率影响因素，发现拱肋的弹性模量和重度对拱桥的自振频率影响最大。

肖光清[9]采用有限元软件Midas Civil建立了考虑桩土效应和不考虑桩土效应的有限元模型，对比分析了桩土效应对结构动力特性的影响。

论文运用SAP2000软件，建立某实际预应力钢筋混凝土连续箱梁桥的有限元模型，采用弹簧单元模拟实际的桩—土相互作用效应，根据“m”法确定弹簧刚度，对比分析不同结构参数下多跨径公路桥梁的自振响应特性，为认识该类多跨连续梁桥的动力特性及抗震分析提供基础。

2 工程概况

论文以某多跨连续梁桥为背景，共3联，其跨径布置为（4×30＋28＋2×40＋28＋3×30）m的预应力钢筋混凝土连续箱梁桥。第一、三联桥梁上部结构为C55预应力钢筋混凝土箱梁结构，下部结构为双柱式桥墩，为C30混凝土结构，桥墩处采用板式橡胶支座，桥台及过渡墩也为C30混凝土结构，桥台及过渡墩处采用滑板支座。第二联上部结构为现浇C55钢筋混凝土箱梁，采用墩梁固结形式，在过渡墩处设置摩擦摆支座。桥型布置如图1所示。

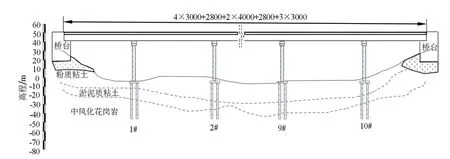
图1 桥型布置图（单位：cm）

3 考虑桩土相互作用的多跨桥梁有限元建模

为分析桩—土效应对长跨径公路桥梁的自振响应的影响，根据该桥的设计方案，采用SAP2000有限元程序，建立三维有限元动力计算模型进行自振动力特性分析，计算模型以顺桥向为X轴，横桥向为Y轴，竖桥向为Z轴。全桥结构均采用空间梁单元模拟，第一、三联桥梁的墩梁连接处为板式橡胶支座，采用弹簧单元模拟，其刚度根据中国公路桥梁板式橡胶支座规范[10]，取刚度7.9×107N/m，第二联桥梁的墩梁连接方式为墩梁固结，采用刚性连接模拟，过渡墩处按为摩擦摆支座，按照实际刚度情况采用一般连接模拟。

桩与土相互作用受力复杂，若将土体对桩的作用力视为线弹性问题，而不考虑其非弹性问题，则可用土弹簧的刚度来模拟土体对桩的作用力。土弹簧刚度系数可由《公路桥涵地基与基础设计规范》中的“m”法计算获得[11]。第n层的土体弹簧刚度系数计算式如下：

式中：an为第n层土的厚度，b1为桩的计算宽度，mn为第n层土的比例系数，hn为第n层土的中心到地面的距离。土弹簧的竖向刚度系数通常将其简化处理，近似为桩的竖向承载力除以竖向相对位移。

利用“m”法建立考虑桩土效应的有限元模型：首先，需要将桩基周围的土体按实际情况进行分层；其次，根据土体情况选取合适的桩基节点位置；最后，通过计算每个节点位置的土弹簧水平刚度系数，用以施加边界条件。全桥共计3070个节点，3040个梁单元，该桥的动力计算有限元模型如图2所示。

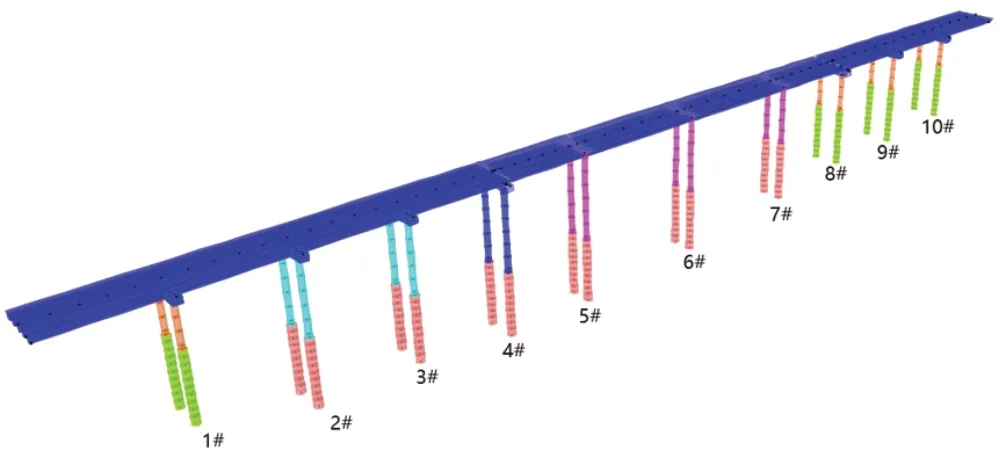
图2 桥梁有限元计算模型

分析和认识桥梁的振动特性是进行桥梁抗震性能分析的基础，桥梁结构的振动特性主要取决于它的各阶自振频率和主振型。在实际桥梁结构中阻尼对自振频率和自振周期计算影响很小，通常忽略不计，因此桥梁的振动方程可简化为：

式（2）具有非零解的条件为：

即（3）式的特征方程为：

4 考虑桩—土相互作用的多跨桥梁自振响应结果分析

论文使用Ritz向量法对该桥的动力计算有限元模型的前90阶模态进行分析，并给出了前5阶模态振型图示，如图3～图7所示。

图3 第1阶振型图

图4 第2阶振型图

图5 第3阶振型图

图6 第4阶振型图

图7 第5阶振型图

由图3～图7的桥梁前五阶模态振型图分析可知，在考虑桩—土相互作用效应下，桥梁第一阶模态振型主要为第一联的振动，体现在墩柱出现纵向（X向）弯曲，桥梁第二阶模态振型主要为第三联主梁的面内转动，桥梁第三阶模态振型为第一联的主梁面内转动，桥梁第四阶模态振型为第三联纵向弯曲振动，桥梁第五阶模态振型为第二联纵向弯曲振动。

为对比不同墩高、桩土相互作用等对多跨连续梁桥自振特性的影响，建立了4种对比工况。工况1为桥梁初始设计；工况2为在工况1的基础上将所有桥墩墩高减少5m；工况3为在工况1的基础上将所有桥墩墩高增加5m；工况4为在工况1的基础上不考虑桩土相互作用影响，直接在墩底固结处理。取桥梁的前10周期进行对比，如表1所示。

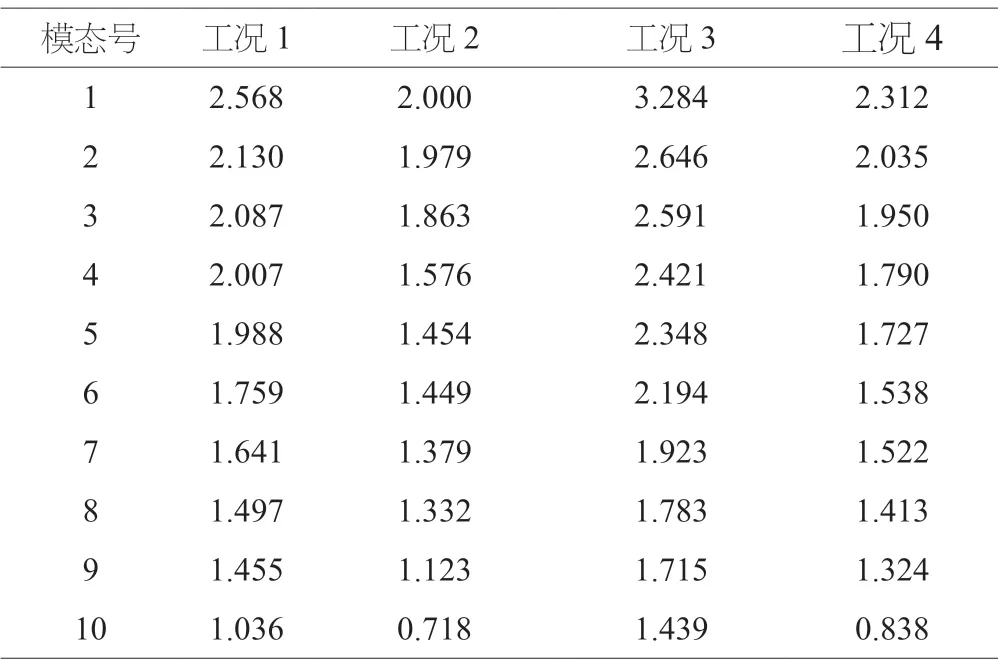
表1 结构前10阶周期（S）

由表格1数据分析可知，结构几何参数对多跨连续梁桥自振特性影响较大，随着墩高增加，结构基本周期明显增加，工况3基本周期较工况2增加了64.2%。其中，桩土相互作用对结构影响也较大，不考虑桩土相互作用的工况4结构自振周期要较考虑桩土相互作用的工况1小，其中基本周期要小10%，说明考虑桩土相互作用后，结构变柔，延长结构基本周期。

5 结语

论文通过建立某山区多跨连续梁桥三维有限元模型，分析了多跨公路桥梁的自振响应特性。得出如下结论：

第一，考虑桩土效应对桥梁结构的振型变化影响不大，但对其自振周期影响较大。因此，对长跨连续梁桥进行抗震分析时，应考虑桩土相互作用。

第二，对于多跨连续梁桥，墩高对结构自振特性影响较大。随着墩高增加，结构基本周期明显增加。