考虑应力敏感效应的裂缝性碳酸盐岩气井拟稳态产能预测方法

李 江， 陈先超， 高 平， 舒成龙

（1.成都理工大学能源学院，四川成都 610059；2.中国石油长庆油田分公司第七采油厂，陕西西安 710000）

研究表明，非达西效应会显著降低气井的产能，能使气井产能降低20%以上[1]。应力敏感伤害是裂缝性油气藏主要伤害类型之一，生产压差或采出速度不合适，或能引发应力敏感，造成储层伤害[2]。压裂直井已广泛应用具有非达西惯性效应的传统二项式产能方程，该方程为现场测试提供了一定的理论基础，例如多点测试、等时测试等[3–4]。但这些研究主要建立在单一孔隙模型上，并且未考虑应力敏感效应的影响。于是，针对致密砂岩气藏、高压海上气藏及页岩气藏，一些学者提出了考虑应力敏感性的各种产能预测模型[5–9]，但这些产能预测模型的计算量通常较大，在实践中应用较为复杂。此外，学者们也提出了一些双重孔隙度模型，来预测双重孔隙度储层的压力或产能[10–15]，但这些模型采用的拉普拉斯、数值反演及大型稀疏矩阵等数值方法过于复杂，也不便于应用[16]。为此，笔者综合考虑非达西效应和应力敏感效应的影响情况，提出了一种用于裂缝性碳酸盐气井的双重介质二项式产能预测模型，以期为裂缝性碳酸盐岩气藏的产能预测提供理论依据。

1 双重介质径向复合气井拟稳态产能方程

1.1 物理模型

碳酸盐岩属于裂缝孔隙型储层，因此考虑非达西效应，采用裂缝基质双重介质模型[17]。双重介质两区径向复合气井的物理模型如图1所示，其基本假设为：1）储层具有双重介质特征，储层全部射开；2）气藏分为内、外两区，内区代表压裂改造区，内区半径为r1，外区半径为re；3）双孔单渗，内外区具有不同的孔渗特征；3）内外区介质间的流动为拟稳定流；4）气井为定产量生产，外边界为定压；5）考虑内区裂缝渗透率变化用于模拟压裂带来的影响。

图1 双重介质两区径向复合模型Fig.1 Dual-media model for radial compound reservoirs with two zones

1.2 不考虑应力敏感双重介质单区气井拟稳态产能方程

在双重介质模型基础上，不考虑应力敏感，双重介质单区气井平面径向流裂缝和基质连续性方程分别为：

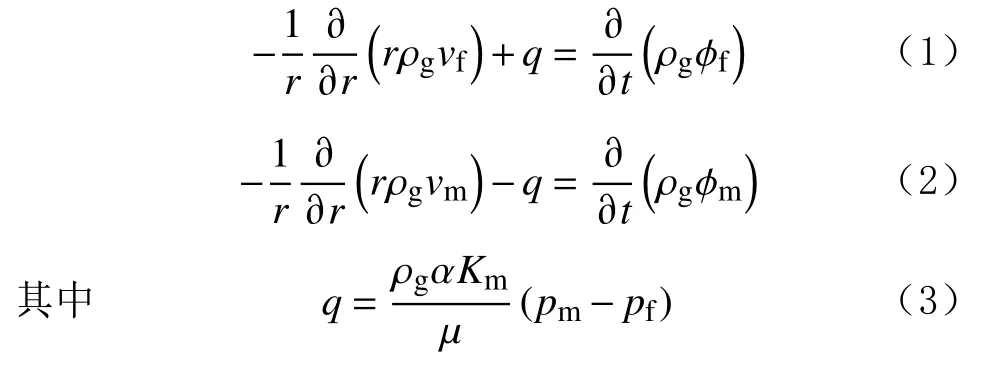
式中：r为径向流半径，m；ρg为气体密度，kg/m3；v为气体渗流速度，m/s；q为窜流量，m3/s；ϕ为孔隙度；p为压力，MPa；α为形状因子；μ为气体黏度，mPa·s；K为渗透率，mD；下标f和m分别表示裂缝系统和基质系统。

根据以上方程，结合内外边界压力已知条件，代入连续性方程并积分，得到二项式产能表达式：

式中：pfe为裂缝系统边界压力，MPa；pfw为裂缝系统井底流压，MPa；Qsc为气井标况下的产量，104m3/d。

考虑表皮效应，得到各系数的表达式：

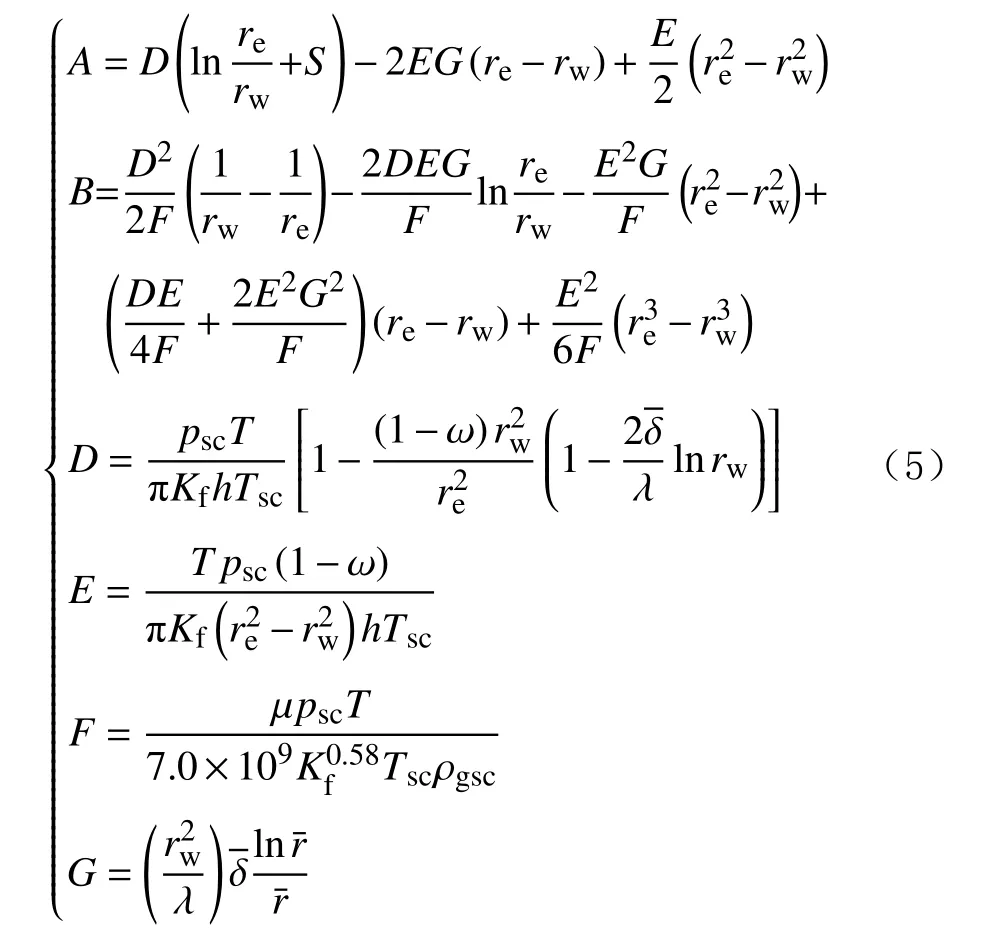
式中：rw为井眼半径，m；re为地层边界半径，m；S为表皮系数；psc为标准状态压力，0.101 MPa；ω为弹性储容比；T为地层温度，K；h为地层厚度，m；ρgsc为标准状态下的气体密度，kg/m3；Tsc为标准状态温度，293.15 K；λ为窜流系数；为平均紊流系数；为平均泄流半径，m。

则无阻流量计算公式为：

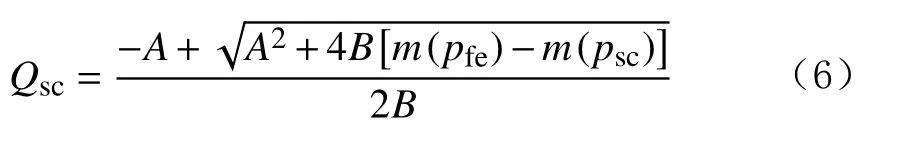
1.3 不考虑应力敏感双重介质两区径向复合气井拟稳态产能方程

基于双重介质单区气井拟稳态产能公式，运用相同的方法推导得到两区径向复合拟稳态产能公式，其二项式产能表达式和式（4）相同。两区径向复合模型中（见图1），压裂裂缝引起的渗流能力变化等效为内区裂缝渗透率变化，即在考虑压裂裂缝时，通过改变Kf1值来模拟压裂裂缝带来的影响。内、外区的其他条件相同，推导得到各无因次系数：

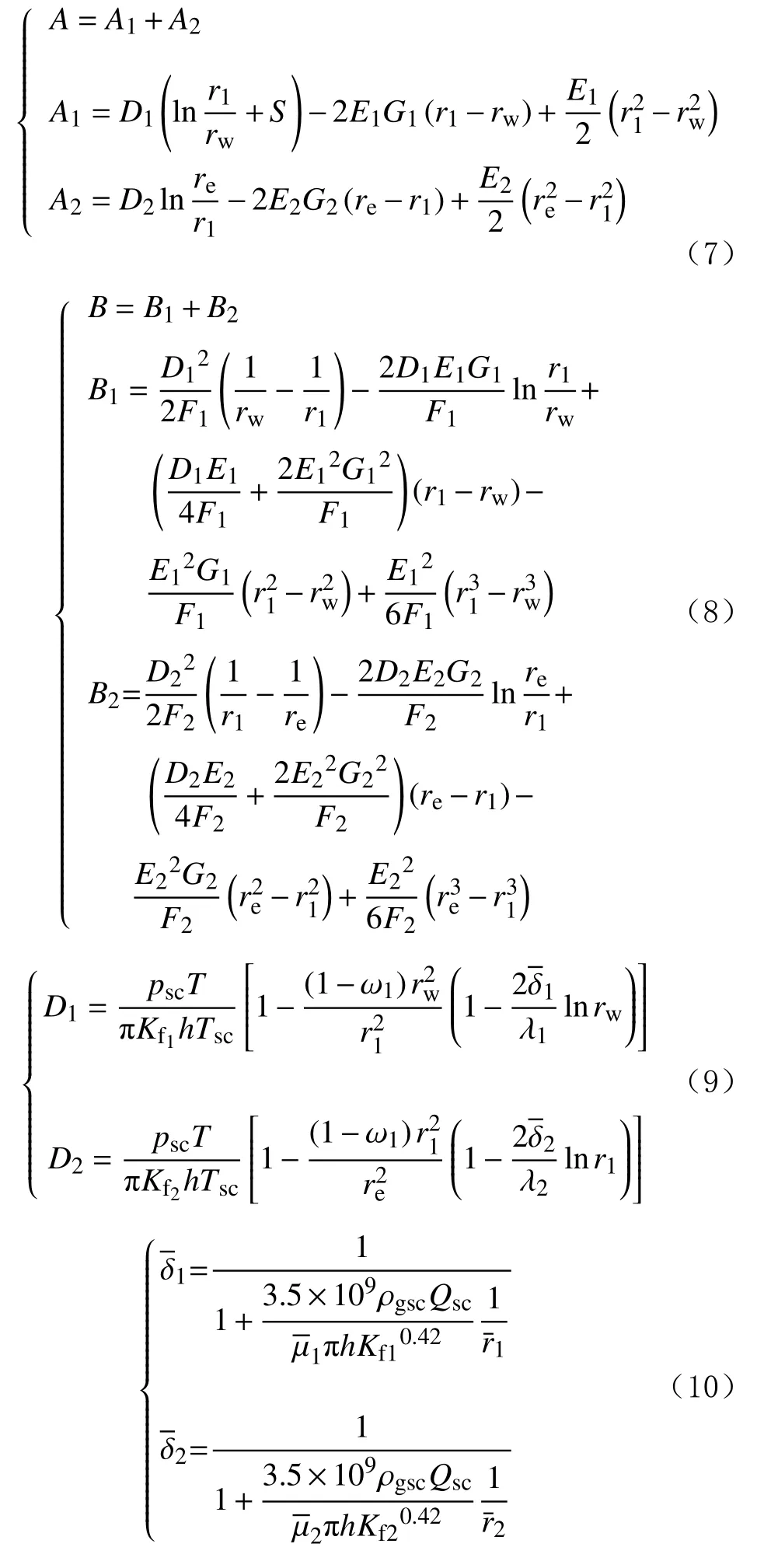
式中：Ct为岩石压缩系数，MPa–1；下标1和2分别表示内区和外区；下标i表示初始状态。

1.4 考虑应力敏感双重介质两区径向复合气井拟稳态产能方程

致密碳酸盐岩储层属于裂缝孔隙型储层，除了考虑非达西效应和应力敏感效应之外，应该采用裂缝、基质双重介质复合模型来计算其产能。因此，基于双孔单渗模型，建立了考虑应力敏感双重介质两区径向复合气井拟稳态产能公式。在不考虑应力敏感模型基础之上，根据文献[18]得到裂缝性碳酸盐岩储层应力敏感关系式：

修正拟压力关系式：

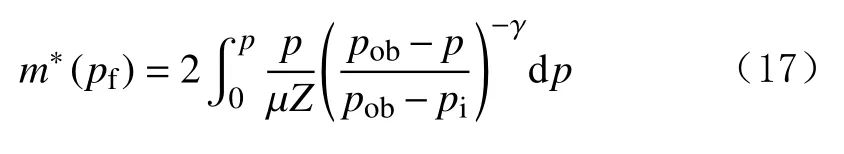
式中：pob为上覆岩层压力，MPa；γ为裂缝应力敏感系数。

对于致密碳酸盐岩地层，窜流系数很小，可以忽略不计。推导过程如前所述，得到两区径向复合拟稳态二项式产能表达式，式中各系数如式（7）—式（15）所示，其中式（13）变为：

2 实例验证

以四川盆地某区块裂缝性碳酸盐岩气藏为例，计算该区块压裂直井A1井的产能。根据双重介质两区试井模型[19]分析得：内区半径r1为99.55 m，内区裂缝渗透率Kf1i为2.08 mD，内区弹性储容比为0.45，内区窜流系数为 5.6×10–3；外区半径re为690.34 m，外区裂缝渗透率Kf2i为 1.89 mD，外区弹性储容比为 0.13，外区窜流系数为 2.0×10–10，双重介质形状因子α为0.6。其他主要参数为：储层中部垂深 5 297.30 m；初始地层压力pi为 58.04 MPa；储层平均孔隙度ϕ为 3.8%，岩石压缩系数Ct为 0.002 MPa–1，标准状态温度Tsc为293.15 K，标准状态压力psc为0.101 MPa，井底温度为 152.62 ℃，井口温度为 40.3 ℃，储层有效厚度 28.10 m，井眼半径rw为 0.044 m，表皮系数S为0.032 2；参考邻井气体组分分析结果，计算临界参数，并利用不同产能模型计算该井的产能。

首先，利用不考虑应力敏感的单区双重介质模型，计算裂缝平均渗透率、平均储容比、平均传导系数、平均压力、平均黏度、平均半径和平均紊流系数，代入式（5）得到A=95.752 6、B=19.406 6，代入式（6）得到Qsc=81.67×104m3/d。

然后，利用不考虑压力敏感的双重介质两区径向复合模型，计算平均压力、内区半径、外区半径、内区紊流系数和外区紊流系数，代入式（7）—式（15），得到的系数见表1，将计算参数代入式（6）得到Qsc=75.40×104m3/d。

最后，用考虑应力敏感双重介质两区径向复合模型，利用径向压力公式计算内区边界压力，然后求算术平均压力，取内区紊流系数 δ1=0.3725，外区紊流系数 δ2=0.9156，代入式（8）—式（12）、式（14）—式（15）和式（18），得到的系数见表1，将计算参数代入式（6）得到Qsc=65.80×104m3/d。

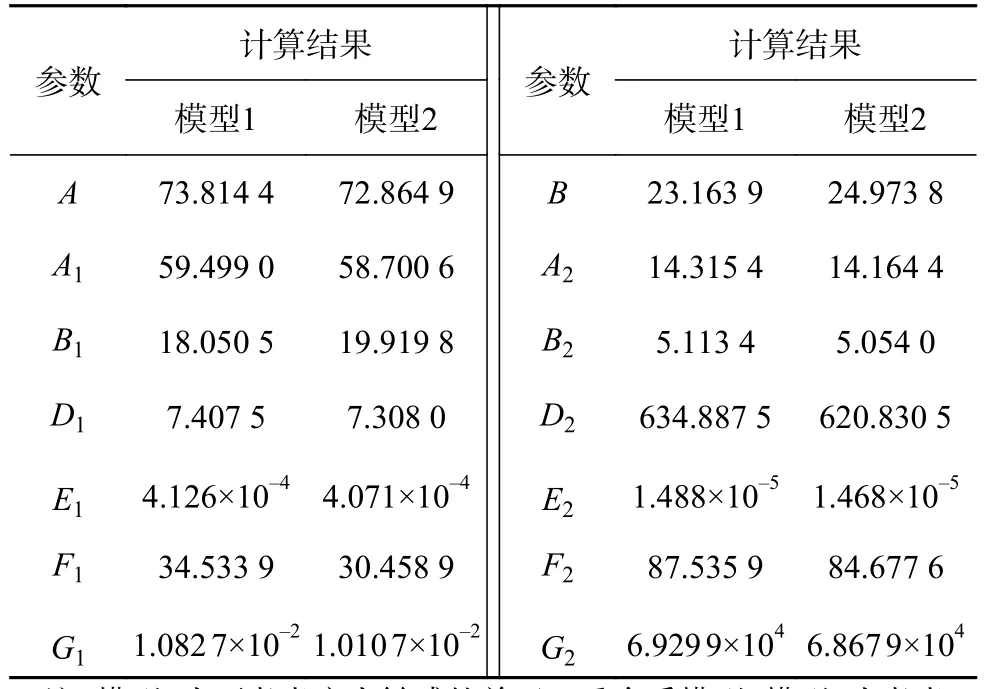
表1 不同产能模型的气井参数计算结果Table 1 Calculation results of gas well parameters from different productivity models

不同产能模型计算结果见表2。从表2可以看出，考虑应力敏感双重介质两区径向复合模型的计算结果与稳定产能试井解释结果（63.83×104m3/d）最为接近，因此考虑应力敏感的产能模型能更合理地预测裂缝性碳酸盐岩储层气井的无阻流量。

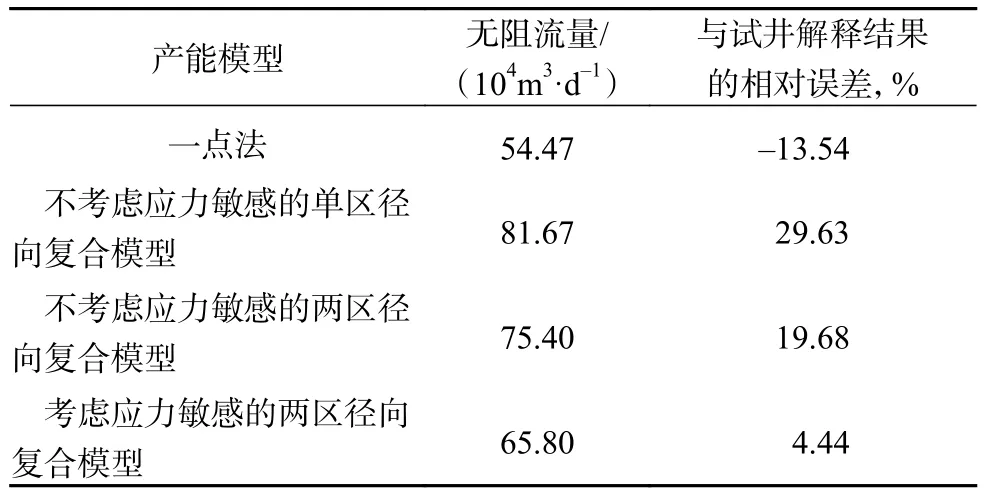
表2 不同产能模型计算结果对比Table 2 Comparisons among calculation results from different productivity models

3 参数敏感性分析

采用控制变量法，变化单一参数，利用考虑应力敏感双重介质两区径向复合气井拟稳态产能方程（计算参数见“实例验证”部分）分析应力敏感系数、上覆岩层压力、初始地层压力及地层系数对生产动态的影响。

3.1 应力敏感系数

其他参数不变，裂缝应力敏感系数γ分别为0，0.2，0.4，0.6和0.8时，气井流入动态曲线如图2所示。从图2可以看出，随着井底流压降低，应力敏感效应越来越明显，应力敏感系数越大，产量降低越明显。实际开发过程中，由于持续开采，将导致储层岩石物性随着应力变化而发生变化，因此需要考虑应力敏感的影响。

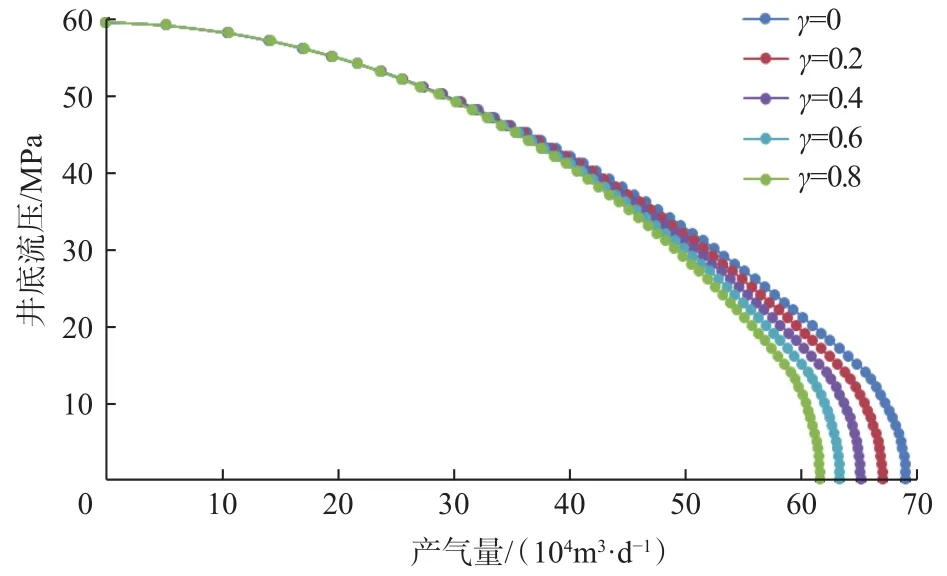
图2 不同应力敏感系数下的IPR曲线Fig.2 Inflow performance relation (IRP) curves under different stress sensitivity coefficients

3.2 上覆岩层压力

其他参数不变，上覆岩层压力pob分别为100，110，120，130 和 140 MPa时，气井流入动态曲线如图3所示。从图3可以看出，随着井底流压降低，上覆岩层压力作用效果越来越明显；上覆岩层压力越小，产量降低越明显。这是因为较低的上覆岩层压力将导致地层能量不足，使产能降低。

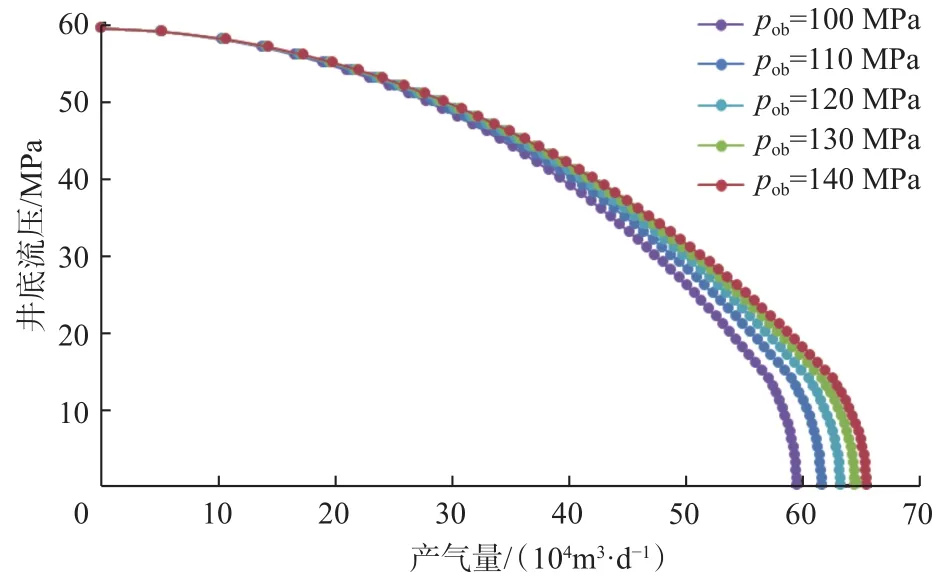
图3 不同上覆岩层压力下的IPR曲线Fig.3 IPR curves under different overburden pressures

3.3 初始地层压力

其他参数不变，初始地层压力pi分别为58.50，59.00，59.42，60.00 和 60.50 MPa时，气井流入动态曲线如图4所示。从图4可以看出，初始地层压力增大，地层能量增大，该作用要比应力敏感作用大；随着初始地层压力增大，气井产量逐渐增大。从流入动态曲线可以看出，随着井底流压降低，初始地层压力降低，产量明显降低；但整体来看，初始地层压力的影响较小。

图4 不同初始地层压力下的IPR曲线Fig.4 IPR curves under different initial formation pressures

3.4 地层系数

其他参数不变，地层系数Kh分别为50.00，55.00，58.07，65.00和 70.00 mD·m 时，气井流入动态曲线如图5所示。从图5可以看出，地层系数对产能影响较为明显，随着地层系数增大，气井产量逐渐增大。从流入动态曲线可以看出，随着井底流压降低，地层系数的作用越来越明显；地层系数越小，产量降低越明显。

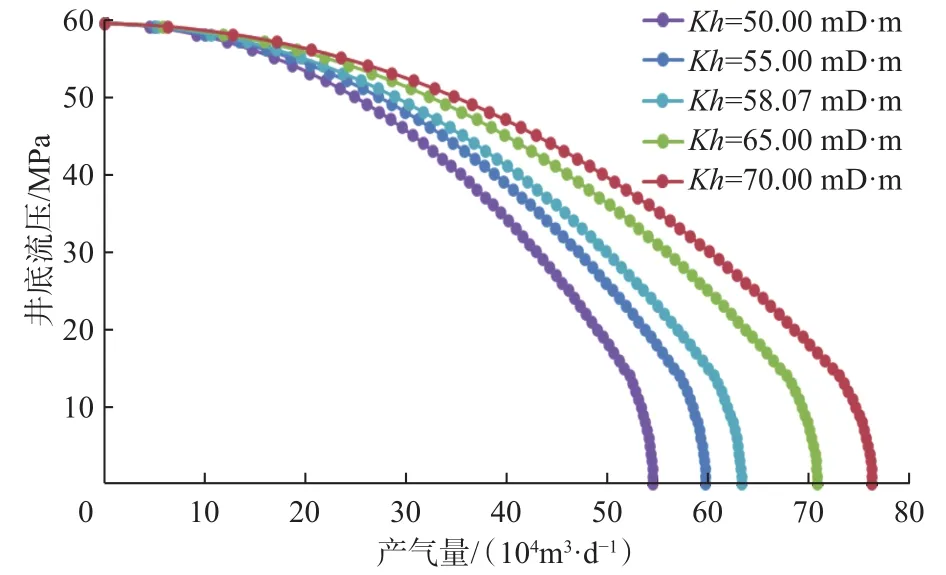
图5 不同地层系数下的IPR曲线Fig.5 IPR curves under different formation coefficients

4 结 论

1）基于双重介质模型，建立了综合考虑非达西效应和应力敏感效应的裂缝性碳酸盐岩气藏产能二项式方程。

2）实例计算和试井解释的气井无阻流量对比表明，综合考虑非达西和应力敏感效应的双重介质两区径向复合模型比一点法的预测准确性更高。

3） 应力敏感性效应对气井产能的影响主要体现在生产阶段后期，产能随应力敏感系数增大而降低；地层系数对气井产能的影响体现在整个生产阶段，产能随地层系数增大而升高。