漠河冻土模拟岩样三轴力学试验及强度多元回归分析

牛成成， 侯绪田， 李 阳

（1.中国石化石油工程技术研究院，北京 102206；2.中国石油大学（华东）石油工程学院，山东青岛 266580）

冻土地层（地层温度低于0 ℃）的岩土力学性质与常规地层有很大不同。冻土中的地层水以冰的形态存在于岩石或土体孔隙中，充当骨架的一部分[1–3]。因此，冻土的土体强度除了与其原始骨架的压实强度有关外，还取决于孔隙中冰的强度[4]。当地层温度低于0 ℃时，孔隙中冰的强度会随温度降低而升高；当温度高于0 ℃时，孔隙中的水将不再具备骨架功能，导致冻土强度骤降[5]。在冻土区进行工程施工时，工程扰动必然导致地层温度场发生变化，而土体强度对温度的依赖性会导致施工风险大大增加。因此，研究冻土地层强度具有现实意义。

由于永久冻土带的工程施工涉及隧道开挖[6–7]、路基施工[8–9]、房屋建设[10]等领域，前人已对冻土基础力学开展了一系列研究。已有研究结果表明，冻土的力学性质会受到围压、环境温度、含水率、应变速率等因素的影响：当围压较低时，土体强度会随着围压升高而升高，其应力–应变曲线特征会由应变软化向着无峰值强度变化[11–12]；在围压较高时，会出现孔隙中冰被压碎、压融现象，土体强度会随围压升高出现降低的趋势[11–13]；围压相同时，环境温度越低，孔隙中冰的强度越高，冻土的整体强度越高[14]；随含水率升高，冻土强度会呈现先线性升高后降低的变化曲线[15]；冻土的峰值强度会随加载时间增长出现降低的趋势，应变速率越大冻土的强度越高[1，11–16]。总体而言，冻土强度受环境温度、地层孔隙度、土体应力状态、孔隙中含水饱和度等多因素的影响，但已有研究大多只聚焦地表工程，忽略地层本身在深度上的差异性。

在油气钻探中，通常需要钻穿整个冻土层，与浅部冻土层相比，深部冻土层的温度要高，承受的压实作用更大、应力更高，孔隙度更低，而这些都会影响冻土的力学性能。浅部冻土层力学性能的研究方法，可以为研究深部冻土层力学性能提供参考，但研究成果不能完全表征深部冻土层的力学性能。因此，开展深部冻土层力学性能研究是开发极地油气资源的重要基础。基于此，笔者对漠河永久冻土进行二次压制，制备了不同深度的模拟岩样，进行了不同温度、围压条件下的冻土低温三轴力学试验，并采用多元回归分析方法分析了压实程度、温度及应力状态等因素对冻土强度的影响，构建了漠河冻土强度计算模型，以期为极地永久冻土层下油气资源的开发提供依据。

1 漠河冻土试验方案与试验结果

1.1 漠河冻土粒径特征与力学试验方案

用取自中国黑龙江省漠河市的冻土土样进行试验。该土样的全岩矿物成分为：石英30%（体积分数，下同），长石42%，铁白云石2%，闪石1%，黏土25%；矿物颗粒的粒径分布为：粒径＜0.357 μm的占0%（体积分数，下同），粒径在 0.357～4.000 μm 的占23.51%，粒径在 4.000～21.000 μm 的占 42.68%，粒径在 21.000～186.000 μm 的占 33.81%，粒径＞186.000 μm的占0%。由此可知，漠河冻土的主要矿物成分为长石、石英和黏土，含有少量铁白云石和闪石，所有成分颗粒的粒径在0.357～186.000 μm之间。

进行冻土试样重塑，即制备不同深度的冻土模拟岩样时，将原冻土烘干、捣碎并加入适量水进行混合，待搅拌均匀后放进内径25.0 mm的刚性圆柱岩心制备装置进行压制，保持初始填充高度60.0 mm，沿轴向加不同载荷（保持加载时间1 h）来模拟不同地层深度的地应力，然后对压制好的模拟岩样烘干处理，称取前后质量差计算所制岩样的孔隙度、密度等参数。模拟不同深度冻土所需压制力及所得岩样的基础参数见表1。

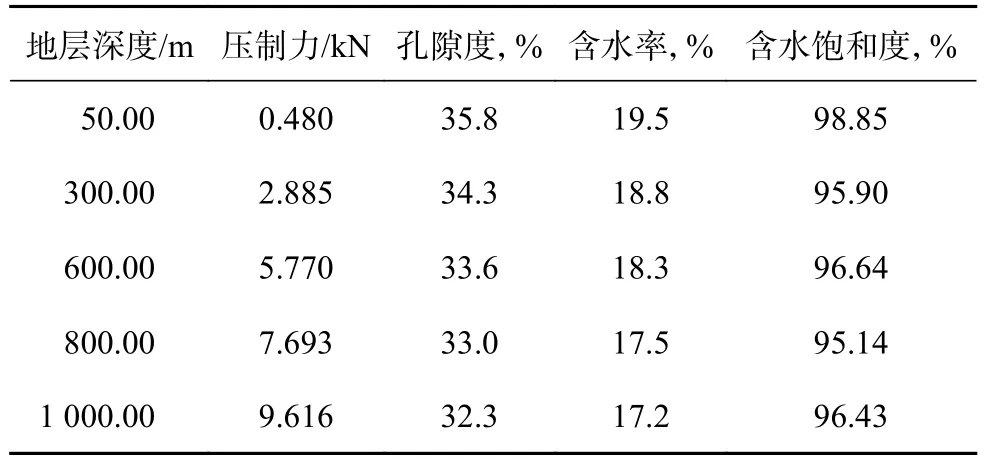
表1 模拟不同深度冻土的压制力及所得岩样的基础参数Table 1 Simulation of compression pressure on frozen soil at different depths and corresponding basic sample parameters

将制备的模拟岩样分别置于设定温度环境下进行冷冻处理（冷冻时间在48 h以上），随后置于低温三轴试验仪进行不同围压条件下的低温三轴力学试验。为此，进行了试验方案设计，结果见表2。

表2 漠河冻土三轴力学试验方案Table 2 Triaxial mechanical test protocol of Mohe frozen soil

1.2 冻土应力–应变曲线与冻土强度分布

通过低温三轴力学试验，可以获得冻土模拟岩样的应力–应变曲线。由于试验数量较大，这里仅以模拟 600.00 m 深处冻土的岩样，在–5 和–15 ℃ 温度、5 MPa围压条件下得到的曲线（见图1）为例进行分析。

从图1可以看出，试验过程中，冻土模拟岩样的应力–应变曲线未出现峰值强度。根据土力学知识，土体变形达到15%～20%时存在严重的坍塌风险，因此，取应变15%对应的差应力作为该温度、围压条件下的冻土峰值强度，得到环境温度–5 ℃下，600.00 m深处冻土模拟岩样在5 MPa围压下的强度为 6.40 MPa，环境温度–15 ℃ 下的强度为 11.35 MPa。利用该方法，可以得到不同深度、温度和围压条件下的土体强度，如图2所示；与之相对应，常温条件下的土体强度如图3所示。

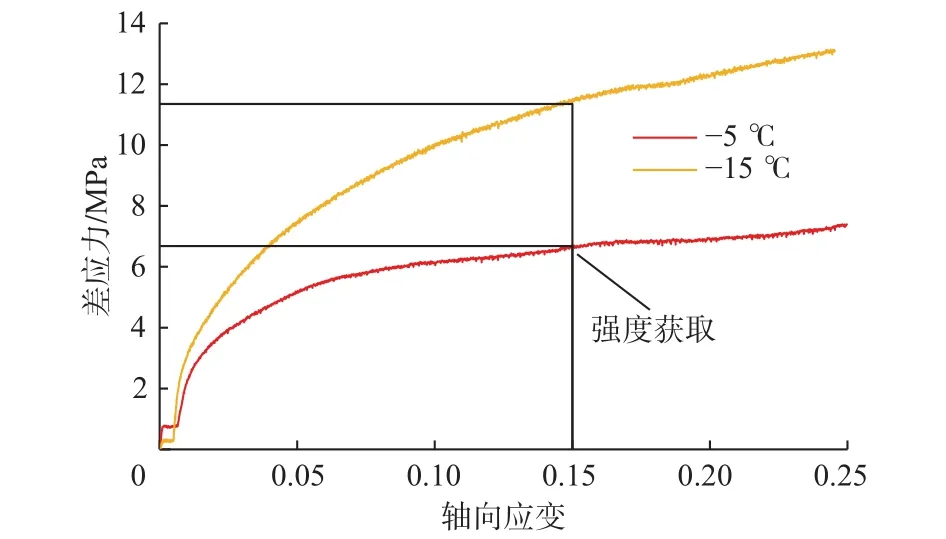
图1 600.00 m深处冻土模拟岩样的应力–应变曲线Fig.1 Stress–strain curves of frozen soil samples at a depth of 600.00 m

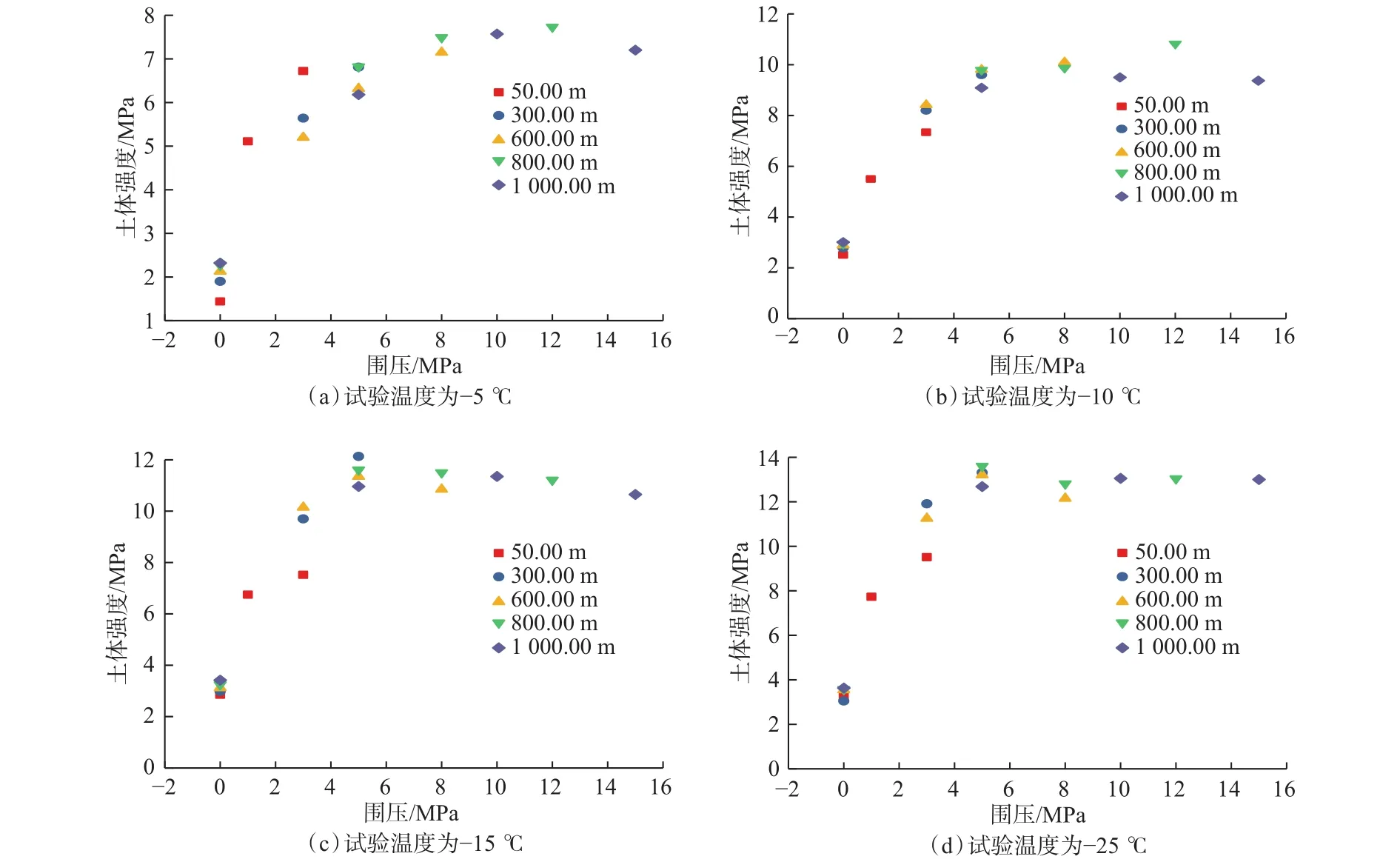
图2 冻土低温三轴力学试验强度散点分布Fig.2 Scatter plots of frozen soil strength based on low-temperature triaxial mechanical test

由图2和图3可知：漠河冻土在非冻结状态下，其强度随深度、围压呈明显的正相关关系；在冻结状态下，其强度与环境温度、围压和土体深度有一定相关性。

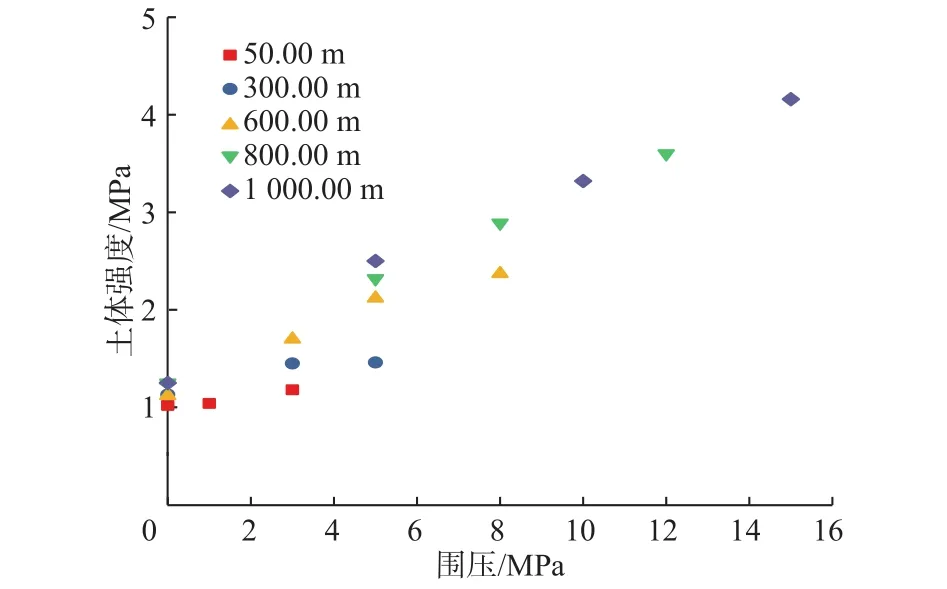
图3 冻土常温三轴力学试验强度散点分布Fig.3 Scatter plots of frozen soil strength based on triaxial mechanical test at room temperature

2 冻土强度多元回归分析

基于漠河冻土三轴力学试验结果，利用SPSS数据统计软件，采用多元回归分析法分析漠河常温土和冻土的强度与各因素的相关性。

2.1 多元回归模型

冻土的强度受多因素影响，如土体埋深、温度、围压等，假设漠河冻土的强度是各个影响因素的连续光滑函数，其表达式为[17]：

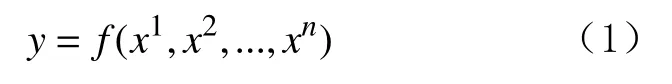
将式（1）在xk处进行泰勒展开：

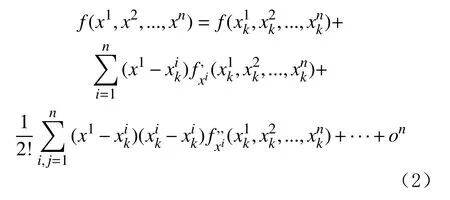
式中：y=f(x1,x2,...,xn)表征土体强度与各因素的函数关系；xi为第i个影响因素；on为泰勒展开后的高阶余项。

任意多元函数都可通过泰勒展开为一系列包含线性相和多次相的多项式，而多元回归模型是一个变量受多个因素影响时，通过假设变量与各因素之间呈现函数关系而建立的分析模型。多元回归模型分为线性回归模型和非线性回归模型。当采用线性回归模型描述时，表明忽略各因素非线性项和交叉项的影响而对模型进行简化，获得各因素与强度之间的近似规律。

先假设冻土强度与温度、围压、深度之间均满足线性关系，可直接得到线性回归模型（否则，剔除这一因素），此时多元线性回归模型的一般形式为：

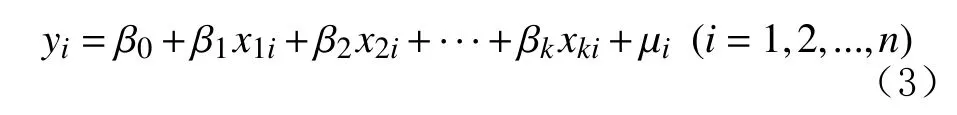
式中：yi为因变量；k为影响因素的数目； β1,···,βk为回归系数；x1i,···,xki为影响因素自变量； β0为截距；µi为残差。

2.2 漠河冻土强度多元回归分析

分析中，首先确定因变量为强度，自变量为深度、环境温度和围压，然后进行因素无关性检验，再进行多元线性回归模型构建和假设性检验。所构建的线性模型为：

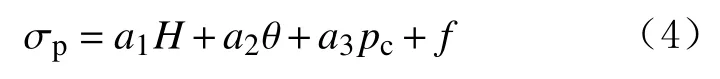
式中： σp为冻土强度，MPa；pc为围压，MPa；θ为环境温度，℃；H为冻土深度，m；a1，a2和a3为回归系数；f为截距，m。

初次回归结果显著性分析结果见表3。

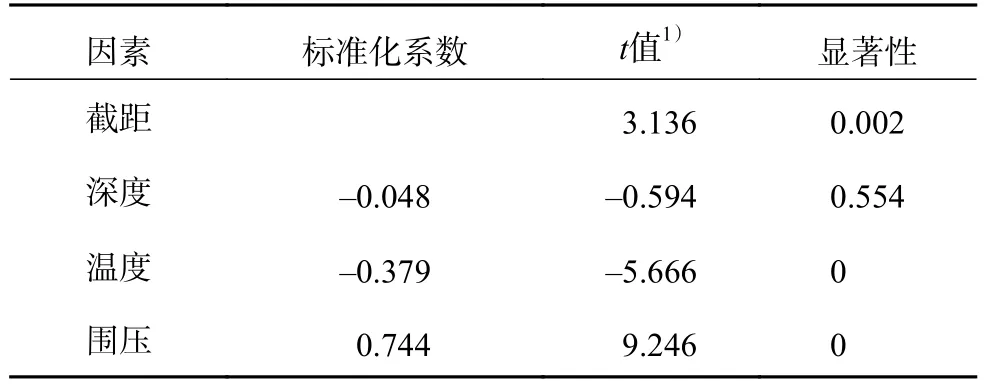
表3 初次回归结果显著性分析结果Table 3 Significance analysis of the initial regression results

从表3可以看出，温度、围压的显著性结果均小于0.050，表明二者与强度之间呈明显的线性相关性，而深度显著性结果为0.554，远大于0.050，表明漠河土在冻结状态，其深度对冻土强度的影响远低于温度和围压，在实际建模中可以忽略深度的影响。

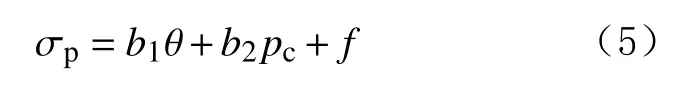
式中： 为回归系数。

即在原有数据中剔除深度，并重新进行多元线性回归分析，结果见表4（其中，调整后的决定系数R2为 0.659）。

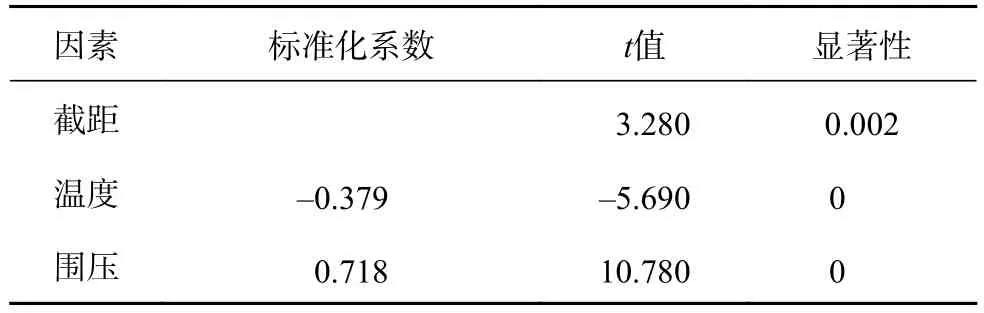
表4 线性回归结果显著性分析结果Table 4 Significance analysis of linear regression results

该模型可解释为，环境温度对强度影响系数为–0.379，即温度每升高 1 ℃，冻土强度降低约 0.379 MPa；围压对强度影响系数为0.718，围压每增加1 MPa，冻土强度增加约0.718 MPa；其多元决定系数R2为0.659，表明线性模型的解释程度为65.9%。可见，用此模型可在一定程度上解释2个因素对强度的影响规律。

然后采用多元非线性回归模型回归漠河冻土强度与环境温度及围压的关系，得到回归关系式：

式中：c1，c2，c3，c4和c5为回归系数。

漠河冻土非线性回归参数估算值见表5（其中，决定系数R2为0.923）。

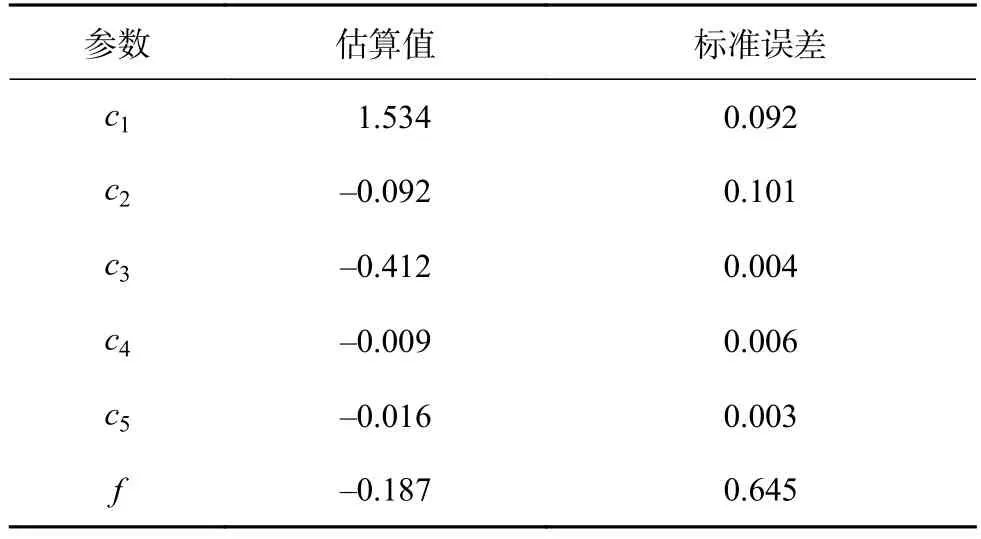
表5 漠河冻土非线性回归参数估算值Table 5 Estimated values of nonlinear regression parameters of Mohe frozen soil

R2为0.923，表明该模型可以解释程度为92.3%，具有较高的冻土强度预测精度。

2.3 漠河非冻结土强度多元回归分析

冻土强度与各因素之间具有很强的非线性关系，因此尝试采用多元非线性回归分析方法建立漠河非冻结土强度与围压、深度的相关关系，得到了其多元回归方程：

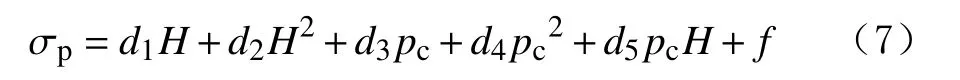
式中：d1，d2，d3，d4和d5为回归系数。

漠河非冻结土非线性回归参数估算值见表6其中，决定系数R2为0.989）。

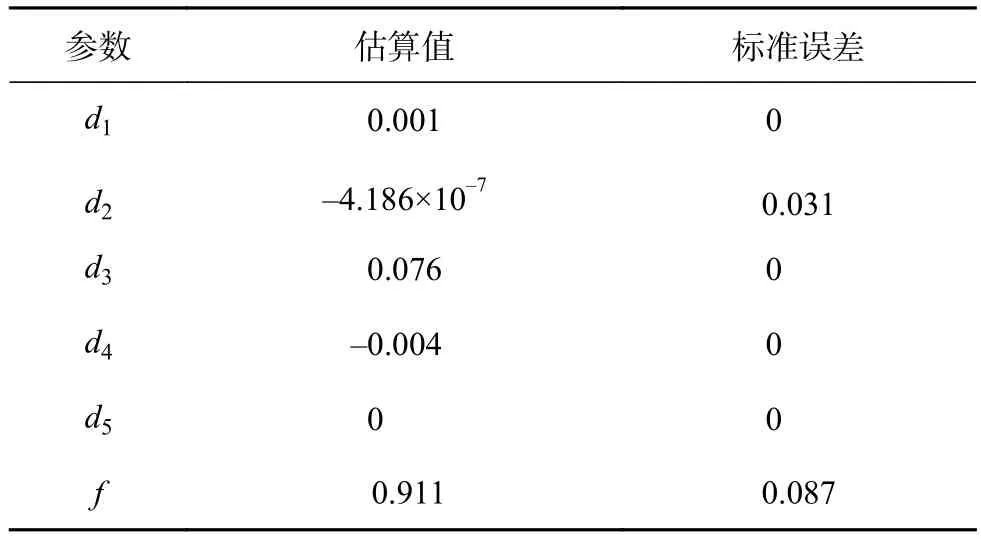
表6 漠河非冻结土非线性回归参数估算值Table 6 Estimated values of nonlinear regression parameters in Mohe non-frozen soil

从表6可以看出，对于漠河非冻结土来说，围压和土体的深度会显著影响土体强度；采用非线性回归模型可以定量解释强度与各因素的相关关系，解释程度为98.9%。

3 漠河冻土强度准则

根据前文的多元回归分析结果，当土体处于融化状态时，其强度只存在骨架强度而没有孔隙中冰的胶结作用，为围压、深度的函数。而当土体处于冻结状态时，其强度由骨架强度与孔隙中冰的胶结作用共同决定。这里可以假设冻结土的骨架强度与土体融化时的骨架强度相同，冻结土强度高出融化土的部分由孔隙中冰的胶结作用产生，即孔隙中冰的胶结强度是围压、温度的函数。因此，漠河冻土强度可表示为：

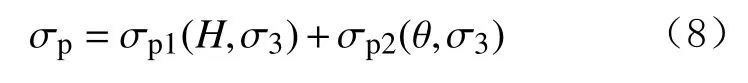
式中： σp， σp1和 σp2分别为冻土强度、融化土强度和孔隙冰的胶结强度，MPa。

当土体处于融化状态时，可利用Mohr-Coulomb强度准则进行描述，其数学表达式为：

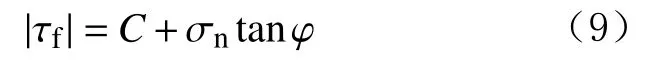
式中： τf为地层的抗剪强度，MPa；C为地层的内聚力，MPa； φ为地层的内摩擦角，（°）； σn为剪切面上的正应力，MPa。

用主应力σ1和σ3对Mohr-Coulomb准则进行描述，并考虑孔隙压力的影响，可得：

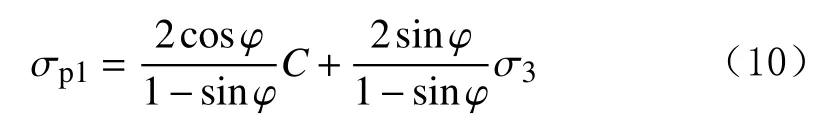
图4为漠河不同深度融化土的莫尔圆。采用莫尔圆法可以获得不同深度土体融化状态下的内聚力和内摩擦角，结果如图5所示。

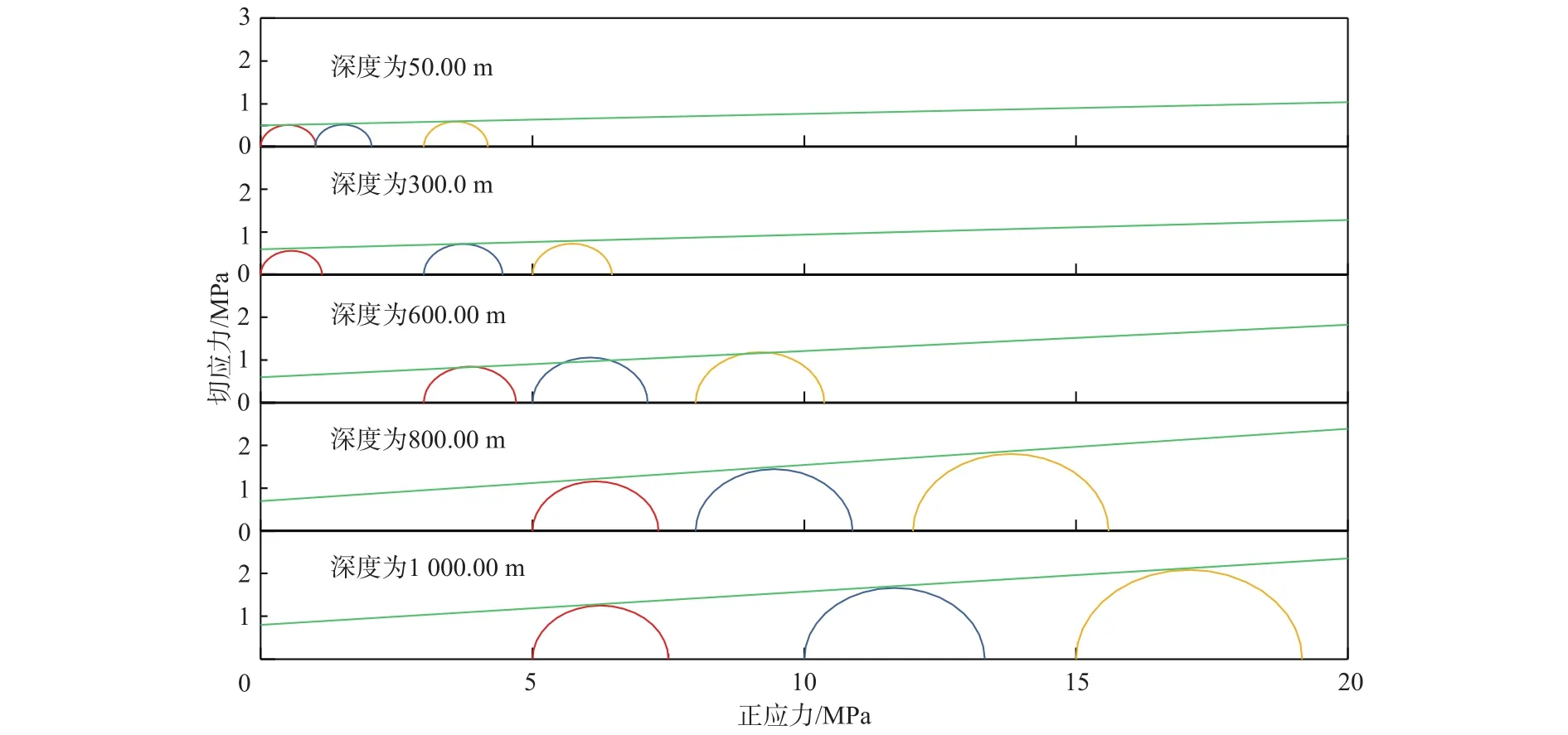
图4 不同深度融化土的莫尔圆Fig.4 Mohr circles of melt soil at different depths

由图5可知，随着冻土埋藏深度增加，土体的内聚力、内摩擦角增大。这是因为土体处于融化状态时，其强度完全由土体颗粒间的胶结及摩擦作用决定，深度越深，土体的初始固结压力越大，颗粒间的胶结及摩擦作用越强，由此导致内聚力、内摩擦角随之增大。对图5中的数据进行拟合，得到内聚力、内摩擦角与深度的关系式：

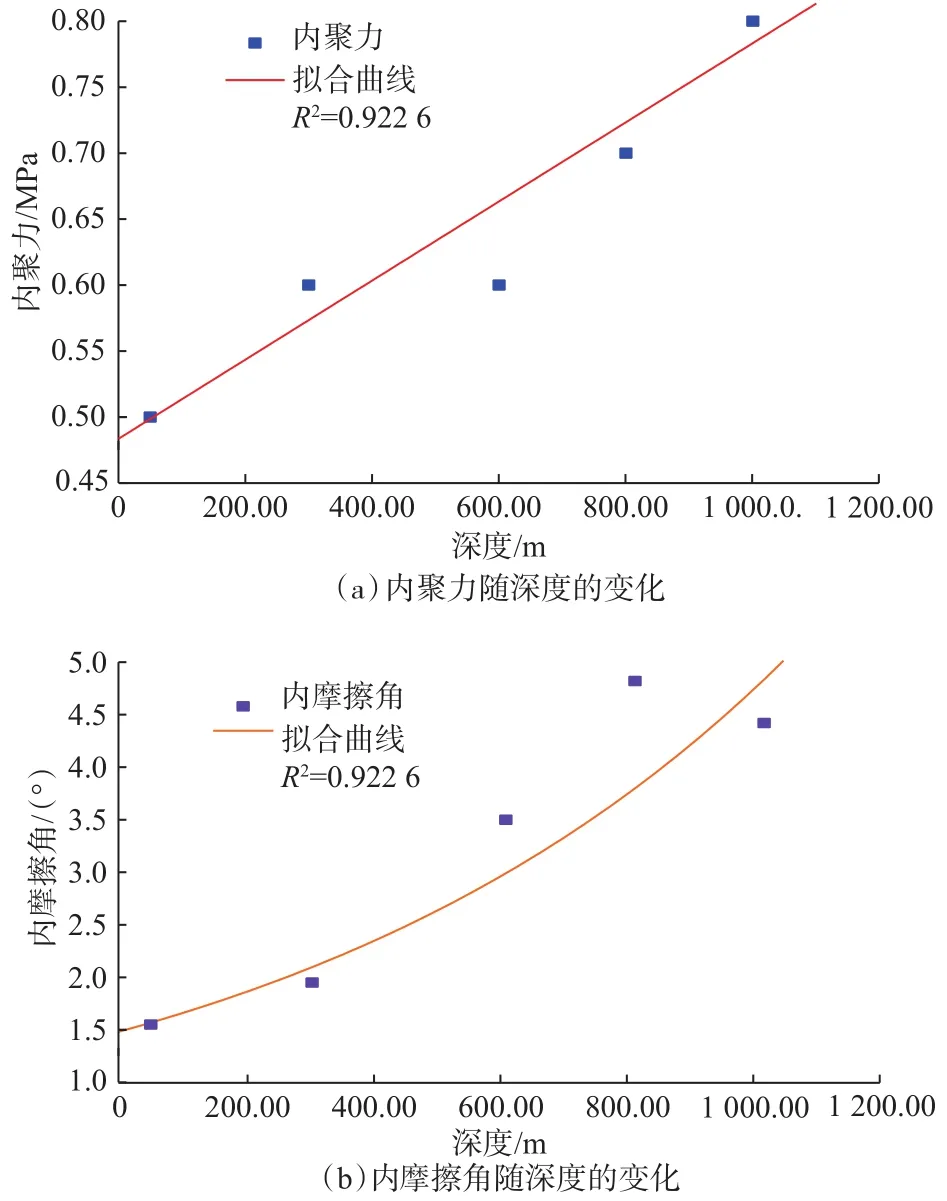
图5 不同深度土体的内聚力和内摩擦角Fig.5 Cohesion and internal friction angles in soil at different depths

对同一温度、围压下不同深度的结果取平均值，表征不同温度孔隙中冰的胶结强度随围压的变化，结果如图6所示。

从图6可以看出，随着试验温度降低，孔隙中冰的胶结强度随之增高；随着围压升高，孔隙中冰的胶结强度呈先升高后降低的趋势，这是因为，孔隙中冰的胶结强度主要由冰自身的强度决定，温度越低，冰自身的强度越高。低围压下，随着围压升高，孔隙中冰的胶结强度增高，这是围压对整体结构的保护作用引起的，与常规土体类似。但在高围压下，高应力状态会导致孔隙中冰出现压融现象而使其强度降低，因此可以采用三次函数表征此现象：

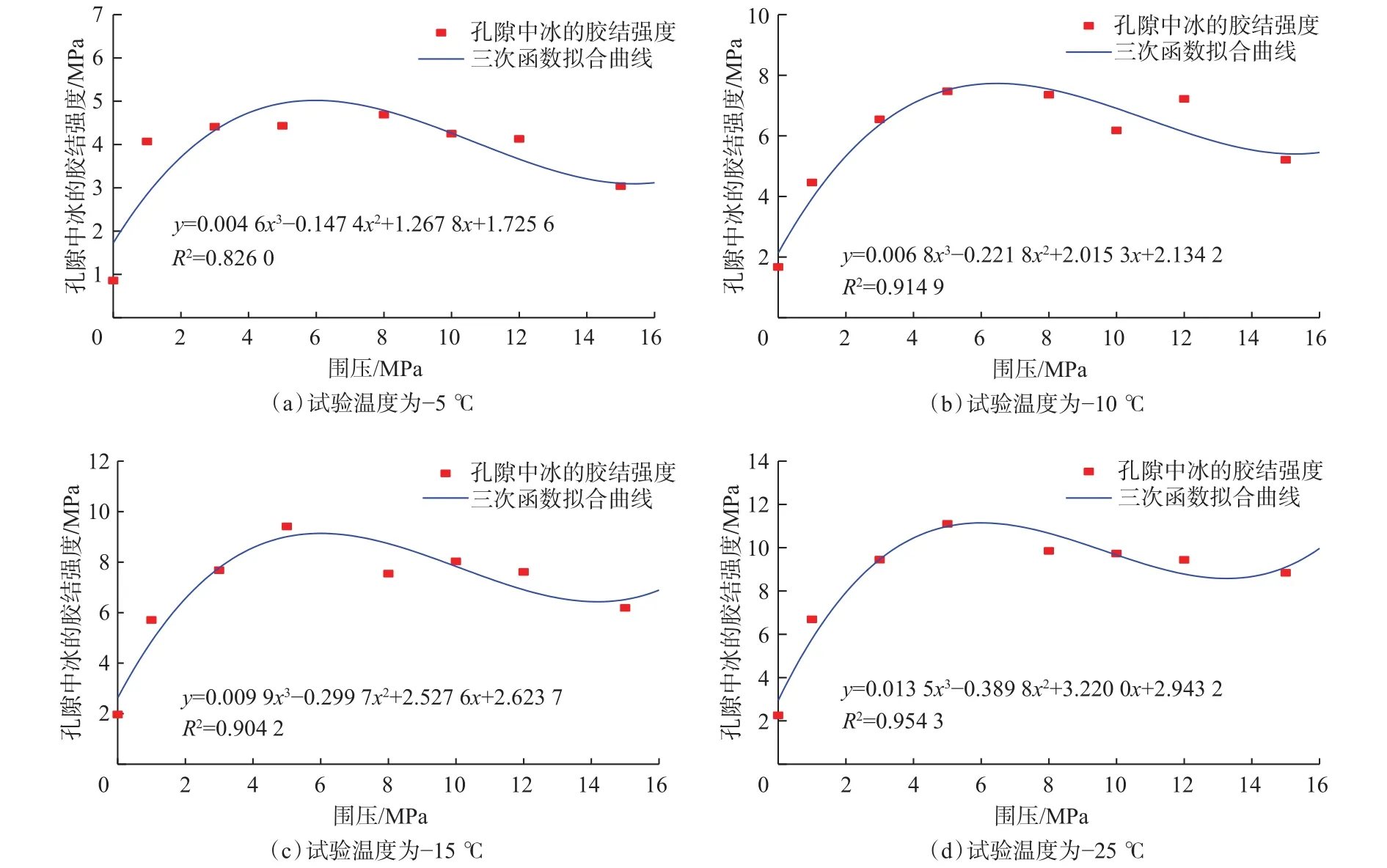
图6 不同温度、围压下孔隙中冰的胶结强度分布Fig.6 Cementing strength distribution of ice in pores under different temperatures and confining pressures

式中：A(θ)，B(θ)，C(θ)和D(θ)为拟合参数，可表征为温度的函数，具体为A(θ)= −0.0005θ+0.0025，B(θ)=0.0121θ−0.0988,C(θ)= −0.0948θ+0.9544,D(θ)=−0.0607θ+1.5214。

为了验证建立的漠河冻土强度计算模型的准确性，将800.00 m深处漠河冻土模拟岩样分别在–15、–5和20 ℃温度下的强度的计算结果与试验结果进行了对比，结果如图7所示。

从图7可以看出，计算结果与试验结果最大相差1.04 MPa，对应的相对误差为22%。可见，所建模型具有一定的精度，可以较好地表征漠河冻土融化–冻结状态下的强度。

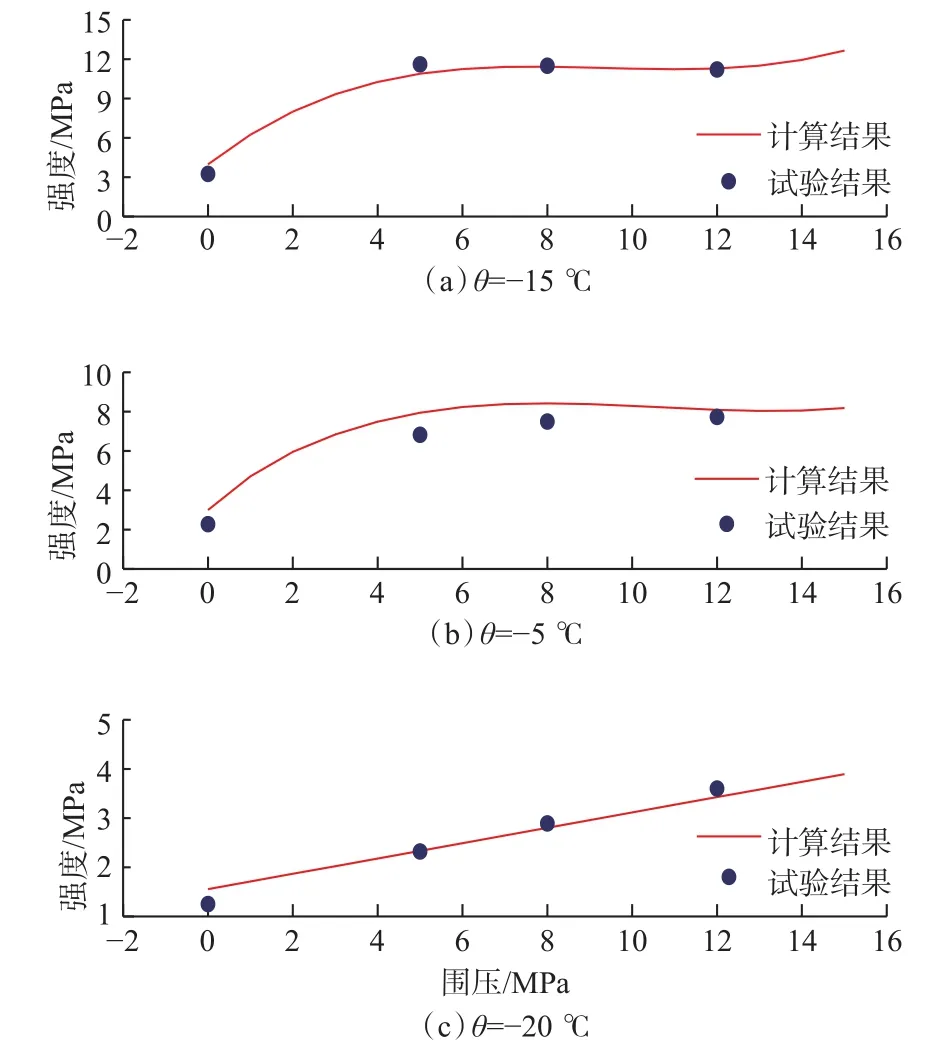
图7 土体强度计算结果与试验结果对比Fig.7 Comparison between calculated results and test results of soil strength

4 结 论

1）通过全岩矿物试验和粒径分析试验，可知漠河永冻土体的主要矿物成分为长石、石英和黏土，并含有少量铁白云石和闪石，所有成分颗粒粒径在0.357～186.000 μm之间。由漠河冻土三轴力学试验结果可知，冻土试样的应力–应变曲线整体呈非线性变形特征，可取应变的15%作为其峰值强度。

2）多元回归分析结果表明，在土体冻结状态下，深度对漠河永冻土体强度的影响较小，围压、环境温度为主要影响因素。围压每增加1 MPa，冻土强度约升高 0.718 MPa；温度每降低 1 ℃，冻土强度约升高0.379 MPa。当土体处于融化状态时，围压和埋深共同决定土体的强度。

3）冻土的强度可视为由土体骨架强度与孔隙中冰的胶结强度共同构成，其中土体骨架强度可采用Mohr-Coulomb强度准则进行描述，其内聚力和内摩擦角随深度增加而增大；孔隙中冰的胶结强度随环境温度降低而升高，随围压增加先升高后降低，可采用三次函数进行描述。

4）构建了漠河冻土强度计算模型，计算结果相对于试验结果的最大相对误差为22%，具有一定的精度，可以较好地表征漠河冻土融化–冻结状态下的强度，可为极地冻土力学特性研究提供参考。