小学数学低年级建模教学应用策略——以《2～5的分与合》教学为例

江苏省南京市南湾营小学 董 智

分与合的内容是在学生已经认识10以内的数，并已积累了一定的数学活动经验的基础上展开教学的。通过让学生经历把几个物体分为两部分，或把两部分合起来的过程，使学生体会分与合的思想。

一、把生活原型作为建模的起点

教师要善于根据学生的具体学情，联系学生的生活实际，寻找教学资源，让学生在已有图式的基础之上衍生出新的图式，既可以拉近数学与生活之间的距离，又能让学生感受到数学与生活之间的紧密联系。这是模型建构的基础和解决实际问题的参照。在情景引入中，教师可以这样进行设计—

片段：在一片美丽的草原上，生活着一只猴妈妈和一只猴宝宝。一天，猴妈妈带着猴宝宝去河对面摘桃子，摘了几个桃？（生答）猴妈妈想出个难题考考猴宝宝，把4个桃放在两个盘子里，你们会放吗？

二、把活动经验作为建模的基点

数学建模的过程要能够与数学活动经验的获得过程相契合。教师可以引导学生通过动手操作的活动获得成功的体验，结合学生的已知能力与水平安排学生活动。

片段：这可难倒猴宝宝了，把4个桃放在两个盘子里，你们会放吗？可以怎么放呢？拿出准备好的4个桃子图片和同桌分一分。

在学生分完桃子后，为了能直观呈现学生的方法，我让学生把黑板上准备的桃子分一分。

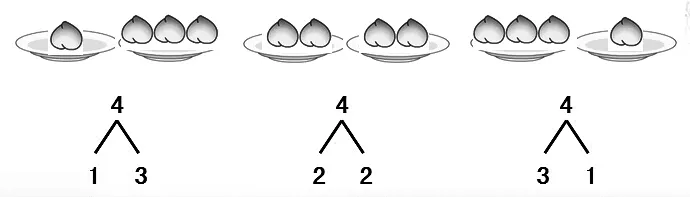
说说你是怎么分的，谁再来说一说他的分法？4个桃可以分成1个和3个。有不同的分法吗？你是怎么分的？4个桃可以分成2个和2个。还有不同的分法吗？你是怎么分的？4个桃可以分成3个和1个。

呈现出以下板书：

三、把数形结合作为建模的支点

小学生年龄较小，他们的思维主要是形象思维，而图形较为直观，因此很容易被学生接受。利用图形进行教学，可以有效地将复杂而抽象的数学问题变得更加简洁而具体，让学生理解起来更加直观。

片段：我们想到了几种分法？第一种分法表示：4个桃可以分成1个和3个，就是把4分成了1和3。

板书：

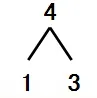
谁来试着读一读？ 4可以分成1和3。（指第二种分法）你会像刚才那样，把这种分法也写出来吗？在练习本上试一试。

板书：

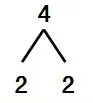
（指第三种分法）谁能上黑板写一写这种分法？

板书：

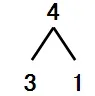
黑板上呈现出4的三种分法，初步构建分与合的基本模型：

四、把提升思维作为建模的重点

教师要能通过创建数学模型来帮助学生解答具体的问题，让学生感受到数学模型所具备的真实价值，体会到学习数学知识的具体用途，有效地树立学生灵活地运用数学知识的意识，并让学生感受到学习给自己带来的独特体验。

片段：观察这三种分法有什么变化和特点。

通过观察总结得出其特点，注重学生的语言训练：几可以分成几和几，几和几合成几，以深入理解4的分与合。教师可以采用多种方法，让学生进行比较体验，进而发现知识之间的差异性以及导致这种差异的具体原因，真正让学生尽快掌握知识的根本。

五、把结构化作为建模的生长点

在较短的时间内使学生经历数学模型建构的活动过程，有效掌握新知结构、特点。结构化的“微建模”是一种尝试，也是一种探索。

片段：小朋友们，你们为猴宝宝解决了难题，它很高兴，送了你们一些小红花，你能把这些小红花也分成两部分吗？ 5可以分成几和几？几和几可以合成5？拿出5朵小红花和同桌分一分。谁来说说你的分法？

板书：

虚线框里的分法与它左边的分法有什么关系？你能根据5的不同分法，说出几和几合成5吗？你能说一说2和3的分与合吗？这就是我们今天学习的内容：2～5的分与合。

这样的学习内容，可以让学生经历建构模型结构化的过程，并在深入探究与解决的过程中进一步感知数学模型的独特性，并可以灵活地运用数学模型。

总而言之，教师要能通过建模教学加深学生对数学知识的记忆与理解，帮助学建立知识结构，加深知识掌握。此外，教师还要注重培养学生自主探究的能力，让学生真正感受学习数学的快乐。