基于KPCA-WOA-KELM的岩爆烈度预测

郭延华，赵 帅

(河北工程大学 土木工程学院，河北 邯郸 056038)

岩爆是隧道开挖时，因岩体受到扰动，其中聚积的弹性能突然释放，导致岩体脱落、爆裂、弹射的动力失稳现象，严重时可造成重大财产损失和人员伤亡[1]。随着我国经济的快速发展，对地下深部资源开采和地下工程建设的需求愈发强烈，对岩爆预测与防治的研究也愈发重要。

在岩爆烈度预测方面，国内外学者进行了大量的研究[2-3]，神经网络[4]、功效系数法[5]、模糊数学[6]、灰色理论[7]、支持向量机[8]、数据挖掘[9]、PCA-PNN法[10]、PCA-OPF法[11]等数学模型与智能算法被提出。但上述预测方法一般基于少量岩爆案例的小样本岩爆数据，而岩爆数据的数量与质量往往影响岩爆预测的准确性和可靠性[12]，所以由此建立的预测模型的可靠性与泛化性较差。此外上述方法的预设参数往往由人工经验设置，预测结果受人主观因素影响较大，或仅对岩爆数据作线性降维，未考虑数据间的非线性关系，从而未充分保留岩爆数据的特征信息。因此在岩爆预测方面需要进一步研究，并提出经济可靠的岩爆预测方法。

核极限学习机(Kernel Based Extreme Learning Machine，KELM)是一种分类预测算法，该算法将核函数与极限学习机(Extreme Learning Machine，ELM)相结合，以提高ELM算法的预测性能。故本文岩爆烈度预测将基于KELM实现，同时为解决因人工设置参数而影响KELM预测效果的问题，使用鲸鱼优化算法(Whale Optimization Algorithm，WOA)寻优KELM的惩罚系数C和核函数参数s以提高其预测性能。此外，考虑到岩爆评价指标之间的多维交叉冗余性，使用核主成分分析(Kernel Principal Component Analysis，KPCA)对岩爆数据集做特征压缩，相比于传统的主成分分析(Principal Component Analysis，PCA)，KPCA能对数据集做非线性降维，从而能更加充分地保留特征信息，以提高KELM的训练速度和预测速度，故本文建立KPCA-WOA-KELM的岩爆烈度预测模型。

1 模型原理与建立

1.1 KPCA理论基础

PCA是对数据做线性降维的传统降维算法，而对具有非线性关系的数据做特征提取时，却无法充分保留数据的特征信息。KPCA在其基础上结合核函数，将数据映射至高维空间中做数据压缩。KPCA能在充分保留数据特征信息的基础上做数据压缩[13]。

1.1.1 KPCA基础理论

使用函数φ将样本映射至高维特征空间RF，映射值为φ(x1)，φ(x2)，…，φ(xn)并使用PCA方法得到协方差矩阵为：

(1)

其特征方程为：

Cν=λν

(2)

式中，λ为协方差矩阵的特征值，ν为特征向量，由式(1)、式(2)可得ν：

(3)

k(xi,xj)=φ(xi)Tφ(xj)

(4)

对于式(2)，任意的k=1，2，…，n，有：

φ(xk)Cν=λφ(xk)ν

(5)

分别将式(1)、式(3)与式(4)带入式(5)可得：

Kα=λnα

(6)

式中，K为k对应的核矩阵，K=k(xi,xj)，α=(α1,α2,...,αn)。

通过式(6)，求得特征值λ1≥λ2≥…λn及其对应特征向量α1,α2,…,αn。选取p(p≤n)个特征值，满足累计贡献率≥85%。新样本φ(xj)投影后的第j(j=1,2,…,p)维坐标为：

(7)

(8)

1.1.2 核函数的选择

核函数的类别一般分为局部核函数和全局核函数，而核函数的选择往往影响KPCA数据降维的效果。为更加充分地保留数据特征信息，本文将两类核函数加权组合从而建立新的核函数。其中核函数参数通过多重实验的方法得出，组合核函数比例系数采用网格搜索法选取最优组合系数，使其贡献率达到最大值。核函数选用高斯核函数(局部核函数)和多项式核函数(全局核函数)：

(9)

k(x,x′)=(γ(x,x′)+c)d

(10)

式中，σ为高斯核函数的待定参数，γ、c、d为多项式核函数的待定参数。

将式(9)与式(10)加权组合得：

η2×(γ(x,x′)+c)d

(11)

式中，η1、η2为组合核函数的比例系数。

1.2 WOA理论基础

WOA[14-15]是受座头鲸捕食行为的启发而提出的一种群智能算法。座头鲸在发现猎物后，会下潜并旋绕，对猎物进行泡泡网攻击，如图1所示。该过程主要经历三个阶段：随机捕猎、环绕猎物以及捕食猎物。

图1 座头鲸泡泡网攻击捕猎行为示意Fig.1 Humpback whale bubble net attack and hunting behavior

1.2.1 随机捕猎

模拟鲸鱼群随机捕猎的方式求可行解，数学模型如下：

D=|C·X*(t)-X(t)|

(12)

X(t+1)=X*(t)-A·D

(13)

式中，X*为当前最优位置向量，t为当前迭代数，D为位置衡量参数，X为位置向量，A和C为控制参数向量，可通过下式计算：

A=2a·r-a

(14)

C=2·r

(15)

(16)

式中：r为任意向量，tMaxlter为最大迭代数，a随迭代次数的增加由2减少至0，从而实现收缩环绕机制。

1.2.2 环绕猎物

环绕更新位置通过螺旋方程来表示：

D′=|X*(t)-X(t)|

(17)

X(t+1)=D′·ebl·cos(2πl)+X*(t)

(18)

式中：D′为最佳位置距当前位置的距离，l为[-1,-2]中任意数；b为对数螺旋形状的常数，通过公式(19)计算。

(19)

求解时收缩环绕和螺旋更新同时进行，各赋予两种方式1/2的概率执行：

(20)

式中：p为[0,1]的随机数。

1.2.3 捕食猎物

探索过程中，通过全局搜索更新最佳位置以达到最优，数学描述为：

D=|C·Xrand-X|

(21)

X(t+1)=Xrand-A·D

(22)

式中：Xrand是当前一代中的随机位置向量。其中|A|<1时，使用收缩环绕局部寻优；|A|≥1时，使用探索全局寻优。

1.3 KELM理论基础

ELM[16]是一种单隐含层前馈神经网络，其学习目标函数F(x)可用矩阵表示为：

F(x)=h(x)×β=H×β=L

(23)

β=H*·L

(24)

式中：x为输入向量，h(x)、H为隐层节点输出，β为输出权重，L为期望输出H*为H的广义逆矩阵。

引入惩罚系数C和单位矩阵I增强神经网络的稳定性，则输出权值的最小二乘解为：

(25)

引入核函数到ELM中，核矩阵为：

ΩELM=HHT=h(xi)h(xj)=K(xi,xj)

(26)

式中：xi，xj为试验输入向量，则可将式(23)表达为：

(27)

式中：(x1,x2…,xn)为给定训练样本，n为样本数量。核函数选用高斯核函数即：

(28)

惩罚系数C和核函数参数s的设置在一定程度上影响KELM[17]的预测性能。

1.4 KPCA-WOA-KELM模型构建

本文岩爆案例基于Zhou等收集的国内外地下工程和矿山中245组岩爆案例[18]。去除部分埋深数据缺失案例后，选取岩爆烈度判别指标并随机将数据集分为训练集174例与测试集30例。

首先利用KPCA对岩爆数据做特征提取，然后将训练集输入KELM进行训练，并使用WOA对其参数优化，最后利用测试集测试该预测模型的准确性。基于KPCA-WOA-KELM的岩爆烈度预测模型的流程如图2所示：

图2 岩爆烈度预测模型流程Fig.2 The process of rockburst intensity prediction model

2 岩爆烈度仿真实验与分析

2.1 岩爆烈度预测指标选取

影响岩爆的因素具有显著的突发性、随机性与复杂性的特点，其主要包括岩性、地质条件、开挖方式、围岩初始应力状态、隧道断面型式等。

目前国内外学者对岩爆预测指标的选取通常基于岩石力学参数或岩爆判据。一般来说，选取岩爆预测指标应符合易于获取、代表性与可操作性强的特点，能从多个方面反映岩爆的特征信息。

根据岩爆的影响因素、特点及成因，本文选取岩爆埋深D，围岩最大切应力σθ，单轴抗压强度σc，单轴抗拉强度σt，应力集中系数SCF(最大切向应力比单轴抗压强度)，脆性系数(单轴抗压强度比单轴抗拉强度B1和单轴抗压、抗拉强度之差与两者之和的比值B2)，弹性能量指数Wet作为岩爆烈度的主要评判指标。将岩爆分为4级：无岩爆、轻微岩爆、中等岩爆、强烈岩爆，其级别分别对应Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级，表1为不同理论判据下岩爆烈度分类标准表[19]。

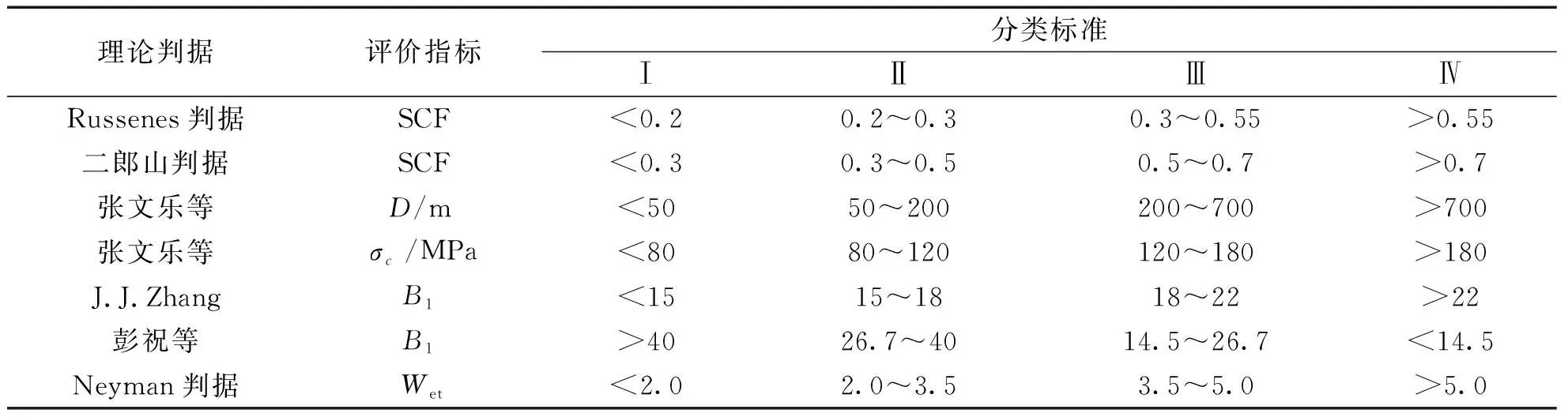
表1 不同理论判据的岩爆烈度分类标准

2.2 KPCA特征提取

KPCA特征提取步骤为：

(1)选取岩爆数据。

(2)归一化初始数据矩阵。

(3)使用核技巧将样本空间映射至高维空间构建核矩阵Kn×n。

(4)核矩阵中心化，即：

(29)

其中，In为元素均为1/n的矩阵。

(5)求解核矩阵的特征值λ，排序特征向量α。选取出p(p≤n)个特征向量，并根据式(8)规范化。

(6)通过特征值和特征向量得出主成分，样本xj在特征向量αk上的投影为：

k=1,2,…,p

(30)

构造特征提取后的矩阵Rn×p。

分别通过组合核函数、高斯核函数和多项式核函数实现KPCA特征提取，其中高斯核函数参数σ=1.81，多项式核函数中d=3，γ=c=1，组合系数η1=0.7，η2=0.3。

表2为通过不同核函数分别得到的特征值，贡献率和累计贡献率。可以看出，组合核KPCA得到70.43%的第一主成分贡献率，远大于高斯核、多项式核KPCA，说明相比于单一核KPCA，组合核KPCA具有更好的特征提取能力。

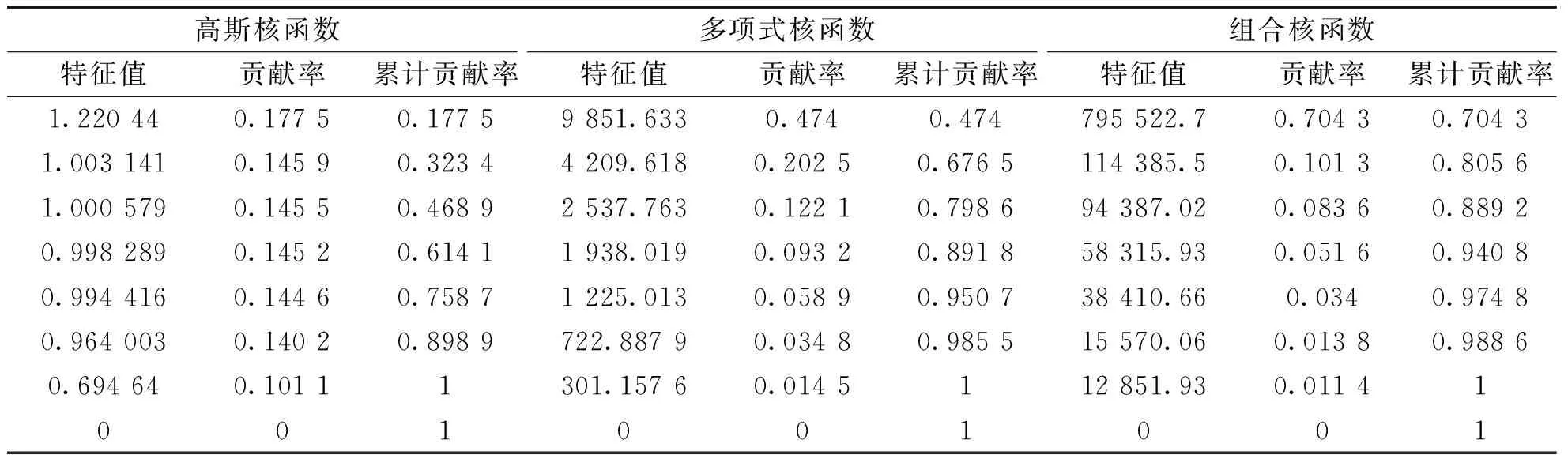
表2 不同核函数特征提取结果对比

2.3 WOA优化KELM模型

由于KELM对其核函数参数的敏感性，直接使用KELM建模，往往导致预测结果产生较大误差。因此，为提高KELM的预测性能，使用WOA算法对KELM的惩罚系数C和核函数参数s进行全局寻优。具体步骤如下：

(1)归一化KPCA降维后的数据集。

(2)参数设置：变量数dim=2、鲸鱼数量SearchAgents_no=30、最大迭代次数tMaxlter=150，变量下限lb=[30,0.2]，变量上限ub=[500,0.7]。

(3)种群初始化：令n=SearchAgents_no，鲸鱼位置为：

(31)

通过下式计算鲸鱼初始随机种群位置X0，迭代数t=1：

X0(i,j)=(ub(i)-lb(i))×rand(i,j)+lb(i)

(32)

式中：X0(i,j)为式(31)第i行第j列的值，lb(i)和ub(i)为第i个座头鲸的下限和上限，rand(i,j)为[0,1]内的随机数。

(5)利用WOA寻优得到最优Cbest和sbest如表3所示。

表3 不同核KPCA下KELM最优参数

(6)将Cbest和sbest代入KELM得到KPCA-WOA-KELM的岩爆烈度等级预测模型。

2.4 KPCA-WOA-KELM模型实测

将30例测试数据输入模型中，结果如图3所示。

图3 不同核KPCA-WOA-KELM岩爆烈度预测结果Fig.3 KPCA-WOA-KELM rockburst intensity prediction results for different core

该模型相关评估指标如表4所示。分别采用F值、准确率(Accuracy)、精确率(Precision)、召回率(Rcall)量化KPCA-WOA-KELM的预测性能。其中Accuracy可量化模型整体的预测性能，其余指标则反映模型对4类岩爆等级中单独的某一级的预测能力。

表4 不同核KPCA-WOA-KELM性能评价

组合核、高斯核和多项式核的KPCA-WOA-KELM的准确率分别为90%、86.66%、83.33%，精确率分别为87.05%、83.92%、84.37%，召回率分别为95%、93.18%、87.62%，F值分别为90.06%、86.69%、83.3%，说明该模型有较高的预测性能。其中，组合核KPCA-WOA-KELM预测能力最优，对4类岩爆等级分类精确率分别为85.71%～100%，85.71%～100%，87.5%～100%，召回率分别为80%～100%，72.73%～100%，72.73%～100%，F值分别为85.71%～93.33%，76.92%～93.33%，66.67%～100%。其中Ⅰ级岩爆与Ⅱ级岩爆的F值均大于Ⅲ级岩爆与Ⅳ级岩爆的F值，说明该模型对Ⅰ级岩爆与Ⅱ级岩爆的预测性能较强，而对于Ⅲ级岩爆与Ⅳ级岩爆的预测性能较弱。

综上所述，综合考虑该模型的准确率及相关评价指标，组合核KPCA-WOA-KELM具有较好的预测性能。

3 工程实践

3.1 工程概况

秦岭终南山公路隧道全程18.02 km，最大纵坡11%。该工程采用双洞双线设计，净宽10.5 m、限高5 m，安全等级一级，结构设计基准期100 a。该隧道深埋地段的最大水平主应力达到21.04 MPa，地应力水平较高，岩爆发生概率较大[20]。

3.2 模型应用

将KPCA-WOA-KELM模型应用于秦岭终南山隧道工程岩爆烈度的预测。该工程岩爆相关指标如表5所示，预测结果与实际情况基本一致。表明KPCA-WOA-KELM在实际工程中有一定的可靠性，为实际工程提供一定的参考价值。

表5 终南山隧道岩爆实测数据与预测结果

4 结论

1)在确定岩爆烈度主要评判指标后，使用KPCA对岩爆数据做非线性降维，相比于PCA,KPCA能更充分保留特征信息，简化KELM模型的输入参数，同时借助WOA优化KELM的惩罚系数C和核函数参数s使其达到最优，从而提高模型的训练速度与预测精度。

2)对局部核函数和全局核函数采用加权方式构造组合核KPCA，并与WOA优化的KELM相结合，建立组合核KPCA-WOA-KELM模型。使用204例岩爆案例对模型进行训练与测试，并用准确率、精确率、召回率、F值等指标综合评价KPCA-WOA-KELM的预测性能。结果表明，组合核KPCA-WOA-KELM相较于单一核KPCA-WOA-KELM有更高的预测性能。

3)为检验该模型的预测性能，将其应用于终南山公路隧道中对岩爆等级进行预测，结果表明与实际岩爆等级基本一致，说明该模型具有一定的工程应用价值。