半实物列车制动系统仿真平台结构设计及空气制动模型解析*
何志浩 樊嘉慧 梁 晖
(同济大学铁道与城市轨道交通研究院,201804,上海 ∥ 第一作者,硕士研究生)
国内铁路货运重载列车的牵引质量已达40 000 t级,因此其制动系统性能至关重要。国内外目前大多采用列车制动系统静置试验台分析列车制动系统性能,但对于长大货物列车,以及多种改型、新型的空气制动机,如果建立庞大的静置试验台,则无法承受巨大的研发成本及超长试验周期。实际上,对于大部分采用空气制动系统的列车而言,虽然每列车的编组不同,但每辆车的制动机性能是相似的。因此,本文提出根据每辆车制动性能的重复性,以及整列车空气波、制动波的传递规律,基于已推导的气体动力学数学模型,建立半实物列车制动系统仿真平台(以下简称“半实物仿真平台”);并以该平台为基础对单一或少量车辆制动系统的状态控制进行仿真分析,通过重复性试验,获得不同编组列车的制动性能。
1 半实物仿真平台结构设计
半实物仿真平台由物理(真机)和数字(模型)两部分有机结合而成。其中,列车制动系统及控制模块是实物部分,而气动力数学模型存于仿真微机软件中,其结构如图1所示。
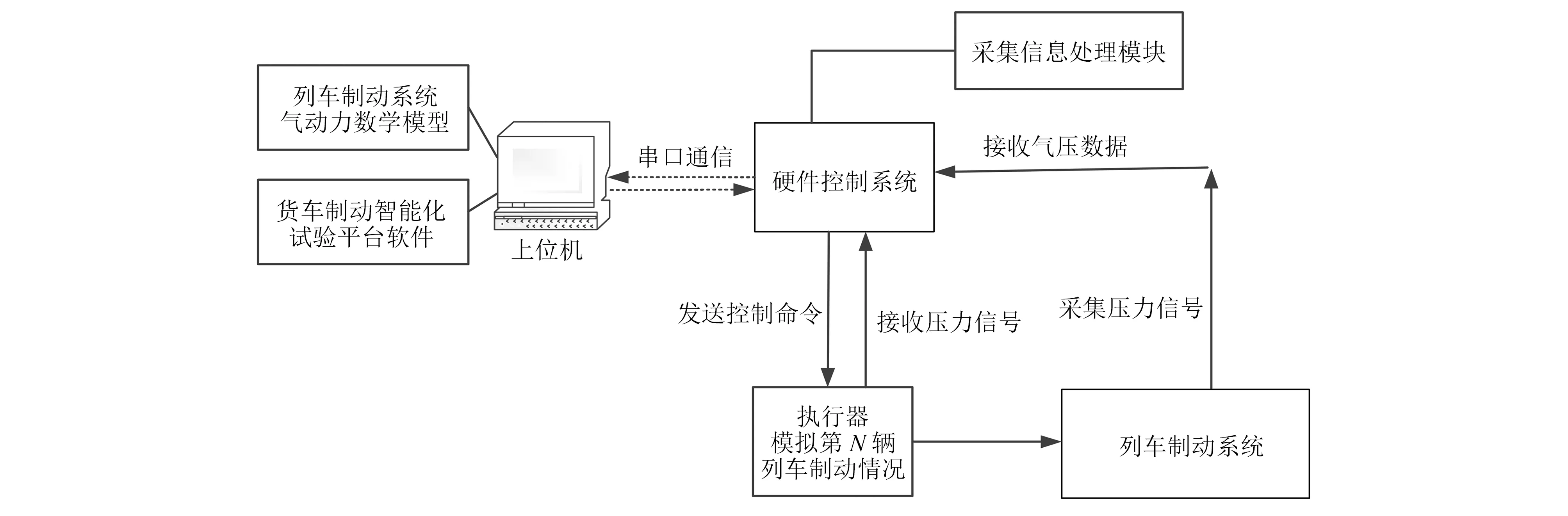
图1 半实物列车制动系统仿真平台组成示意图
半实物仿真平台由上位机和硬件控制系统、执行器和采集数据的传感器组成。上位机安装有C#和matlab软件,完成建模、实时修正及气压信号监控等工作;硬件控制系统上运行的实时操作系统,完成气压信号的发送及反馈;执行器根据接受的硬件控制系统处理后的电流信号,对后端的列车制动系统进行初充气、制动及缓解;传感器将采集的列车制动系统中管路及风缸的气压数据,传送到硬件控制系统中进行实时处理,并在上位机上显示试验气压曲线。上位机上的软件根据试验气压曲线,结合修正系数及因子对气动力学模型进行实时性精确修正。
半实物仿真平台具有独特的数据流设计和实物验证功能,对研究货运列车空气制动系统的制动性能有重要作用。建立合理的列车管路及制动风缸内部气压变化模型,对于研发新型制动机或是改进不同编组货运列车制动系统的制动性能而言,是最需要的核心工作。而对于半实物仿真平台的智能化而言,所采用的气体动力学数学模型是否适用则是成功与否的关键。
2 半实物仿真平台列车制动测试方法
2.1 列车制动管路系统
将列车制动管路系统规范为形象化模型,有助于对列车管内部各点状态变化求解过程的展开。因此,可以将列车制动管路系统看作是由一条笔直的列车管道及沿该管道单侧布设的多个单车系统分支组成[1]。列车制动管路系统结构如图2所示。
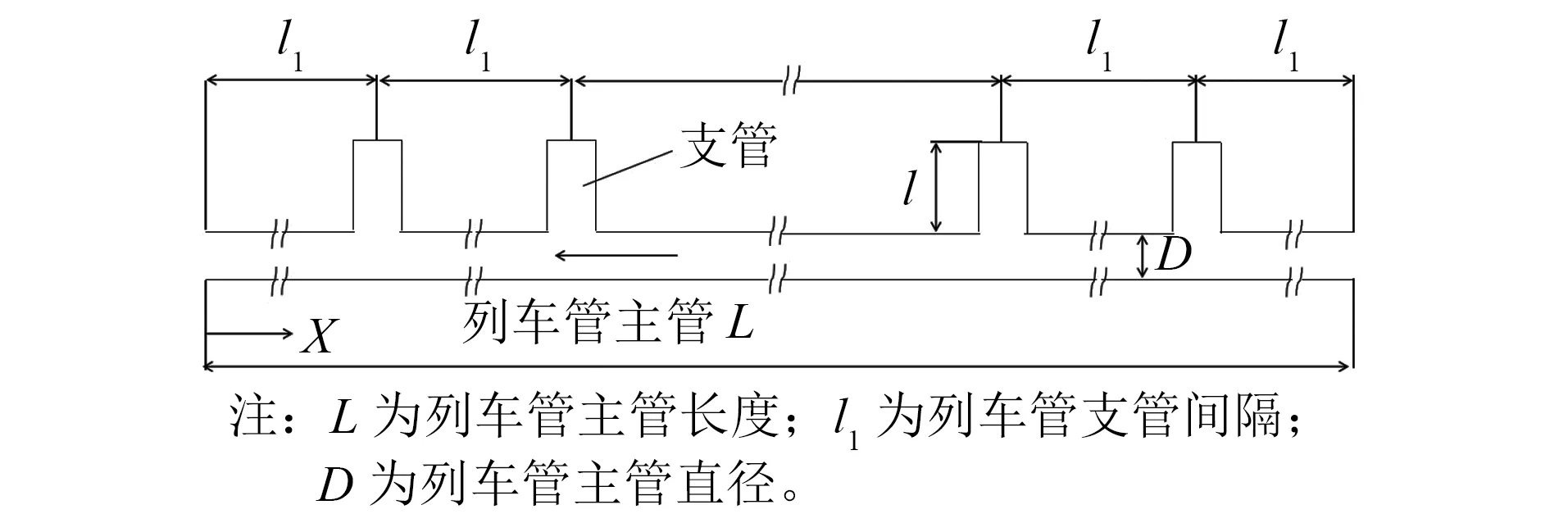
图2 列车制动管路系统结构图
2.2 列车制动测试方法
半实物仿真平台主要测试列车制动在初充气以及各种工况下的制动作用和缓解作用。因此,该平台的列车制动测试要求是:根据已有的制动系统添加传感器实时向上位机发送数据,并根据修正后的模型控制执行器,精确、实时测试列车制动管路的压力变化。
半实物仿真平台模拟整列车不同位置车辆的列车管进风和排风压力以及时间。以控制列车管进气口气压和时间为主,以控制小编组列车车辆排气口排风气压和压力变化为辅。因此,需要控制比例电磁阀以及均衡风缸充气和排风,以模拟制动不同阶段气压上升和下降规律。
单节车辆制动单元前部制动控制执行器的进气管路接风源,排气管路接列车管头部软管;单节车辆制动单元尾部排气控制执行器的进气管路接风源,排气管路接列车管头部软管。两者同时控制比例电磁阀、中继阀和列车制动管。
采用前、后执行器的双执行器控制方式进行小编组级联制动试验。以列车尾部车辆前后方的列车管压差及排气时间作为控制模型,该制动单元前部执行器按照正常进(排)气,同时该制动单元尾部执行器按照不同编组列车根据经验及仿真获得的排风持续时间控制列车管压差。以此为基础,采集列车排气气压曲线,并将该曲线作为下一轮列车充气的气压控制曲线,进行反复级联充气、制动、缓解试验,直至完成目标大编组列车制动试验。半实物仿真平台的制动执行系统由制动控制执行器和车辆制动系统(带有数据采集传感器等)组成。
制动控制执行器(见图3)由多个通断电磁阀、比例电磁阀、均衡阀等核心部件组成,并配有均衡风缸、压力传感器、进排气管路及电源,可实现对列车管各级充气缓解以及排气制动时压力的精确控制。

图3 制动控制执行器实物图
3 列车管充放气数学模型
在气动系统流体力学中,可以借用几个简单的基本过程来描述复杂抽象的气容充放气过程[5];也可以利用等效的节流孔来有效代替阀或者装置内部繁复的通路结构[6]。所以在构建货车制动系统数学模型时,制动系统内部气体在不同工况下的流动则可以简单看作是几个气容之间的充放气过程;并且可以运用有效节流系数替代折角塞门、弯管等结构对气体流动的影响。
在空气制动系统中,制动过程中列车管压力变化主要在于整列车长度上宏观减压和增压效果,故在本研究中将列车管简化为相应的等效风缸来对其压力变化规律进行研究。充分分析制动管路和阀件在气压变动和平衡过程中的作用和原理,在此基础上,建立一个符合充、排气基本规律的主导结构模型。对于气流在管道内部的复杂变化,在主导结构模型可能的变化位置,采用修正系数或影响因子来替代复杂的变化过程。
本文以120型空气制动机为研究对象,建立了货物列车制动系统列车管在初充气及制动时的数学仿真模型。模型运用有效节流系数替代折角塞门、弯管等结构对气体流动的影响。
3.1 列车管初充气
列车管初充气实质上是总风缸向列车管充气的过程。研究制动系统升压或减压的宏观规律时,气体在管路内部的波动可不予考虑,所以可借助一个相同容积的气容来等效替代列车管主管与支管,并通过有效节流系数S修正误差。
列车管的初充气过程利用气容的充气特性描述,图4为总风缸(风源系统)向列车管初充气的简化示意图。空气压力为ps的总风缸经过通路向初压为Pl0的列车管等效风缸充气,并单纯用一个节流孔等效代替总风缸与列车管间的通路结构。
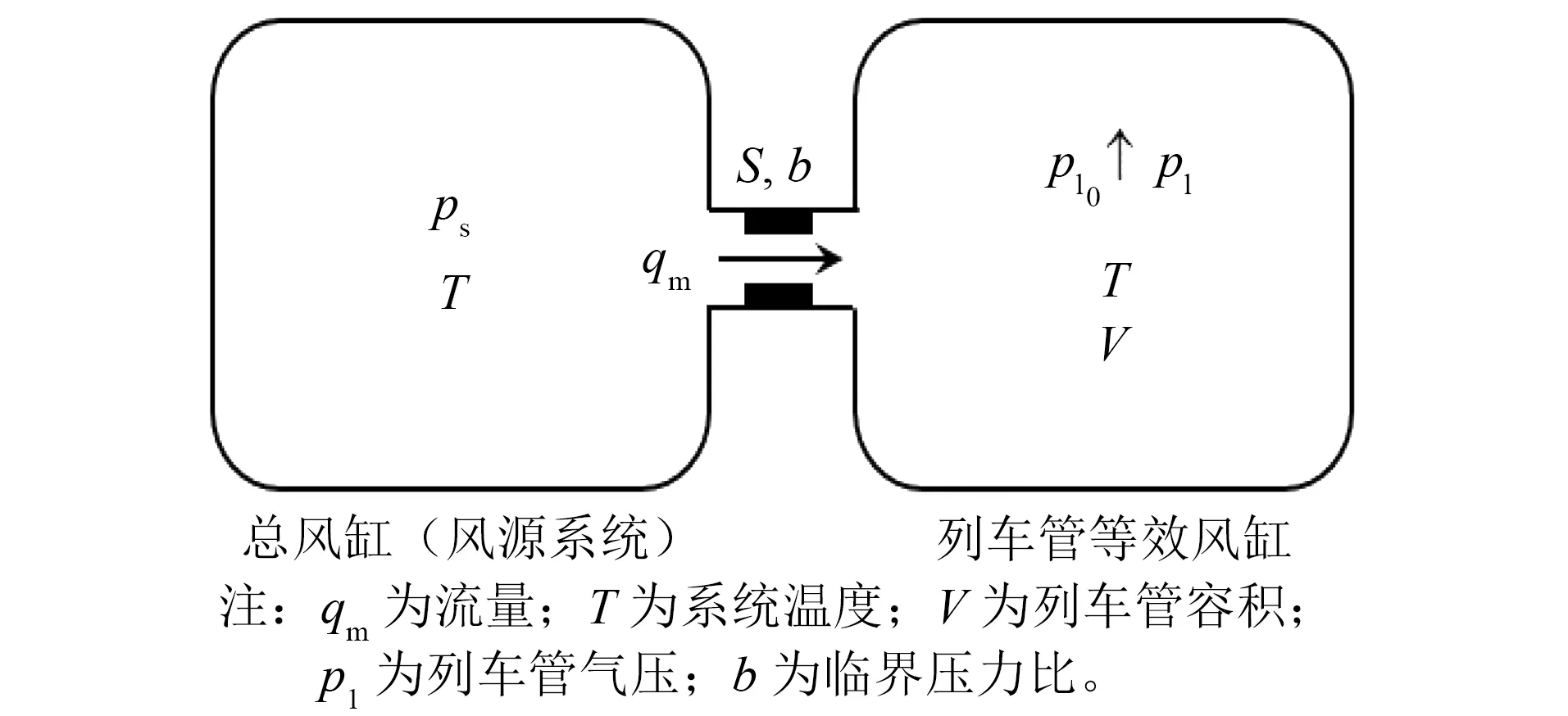
图4 列车管初充气简化模型
在列车管从无空气压力充至500 kPa的过程中,气体的流动在理论上应该包括声速与亚声速两个过程。而气体在声速与亚声速状态下经过通路的质量和流量是不同的,所以初充气过程中列车管压力随时间的变化也应存在声速和亚声速两个阶段。
列车管的容积V(单位为m3)为:
(1)
式中:
N——车辆数,辆;
L——单车的列车管主管长度,m;
D2——列车管支管的直径,m;
L2——单车的列车管支管长度,m。
根据气体在等温充气放气时的方程,可得pl关于时间t的函数(见式(2))。
设定风源压力为ps(单位为kPa),系统温度为T(单位为K),列车管主管的长度为L(单位为m),列车管初始压力为pl0(单位为kPa),则列车管初充气时,pl(单位为kPa)随t(单位为s)变化的关系式为:
(2)
3.2 列车管制动工况
在常用制动列车管减压的研究过程中,可将列车管减压模型简化为如图5所示的模型。列车管的放气特性将根据气容放气特性来近似模拟,该过程产生的误差,通过结合修正函数及影响因子进行修正。图5 a)表示列车管发生第1阶段局减作用时的简化模型,初始压力为pl0的列车管压力空气排入大气的同时进入局减室;图5 b)表示列车管发生第2阶段局减作用时的简化模型,第1阶段局减结束后,列车管压力空气排入大气的同时进入制动缸。列车管减压时的复杂通路初步简化为一个等效的节流孔。同时,增加局减影响参数k来表示局减阶段因气体流动的通路不同而导致的减压特性。
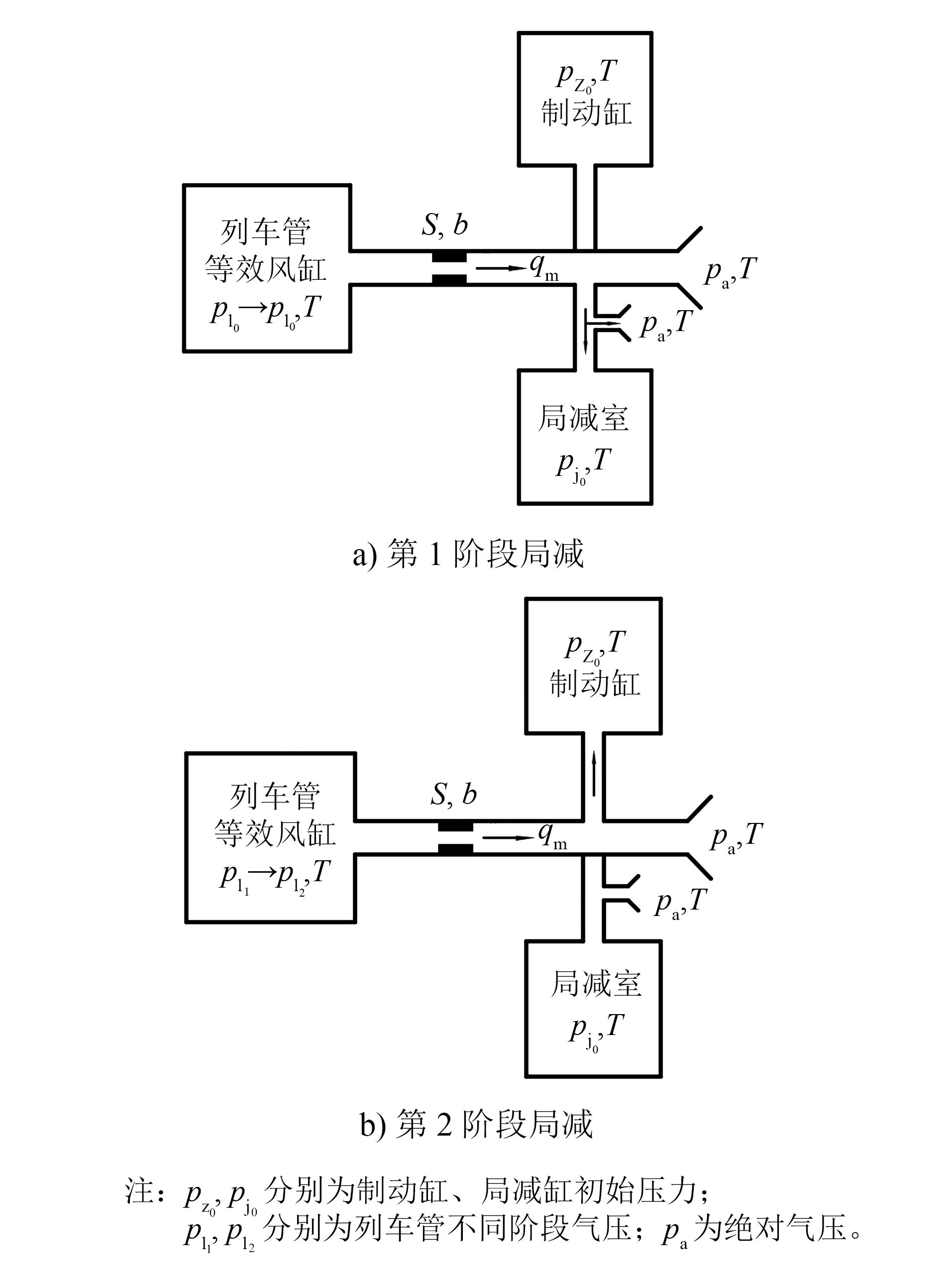
图5 常用制动列车管减压简化模型
根据判断条件,列车管放气过程包括声速放气和亚声速放气两个过程,则:
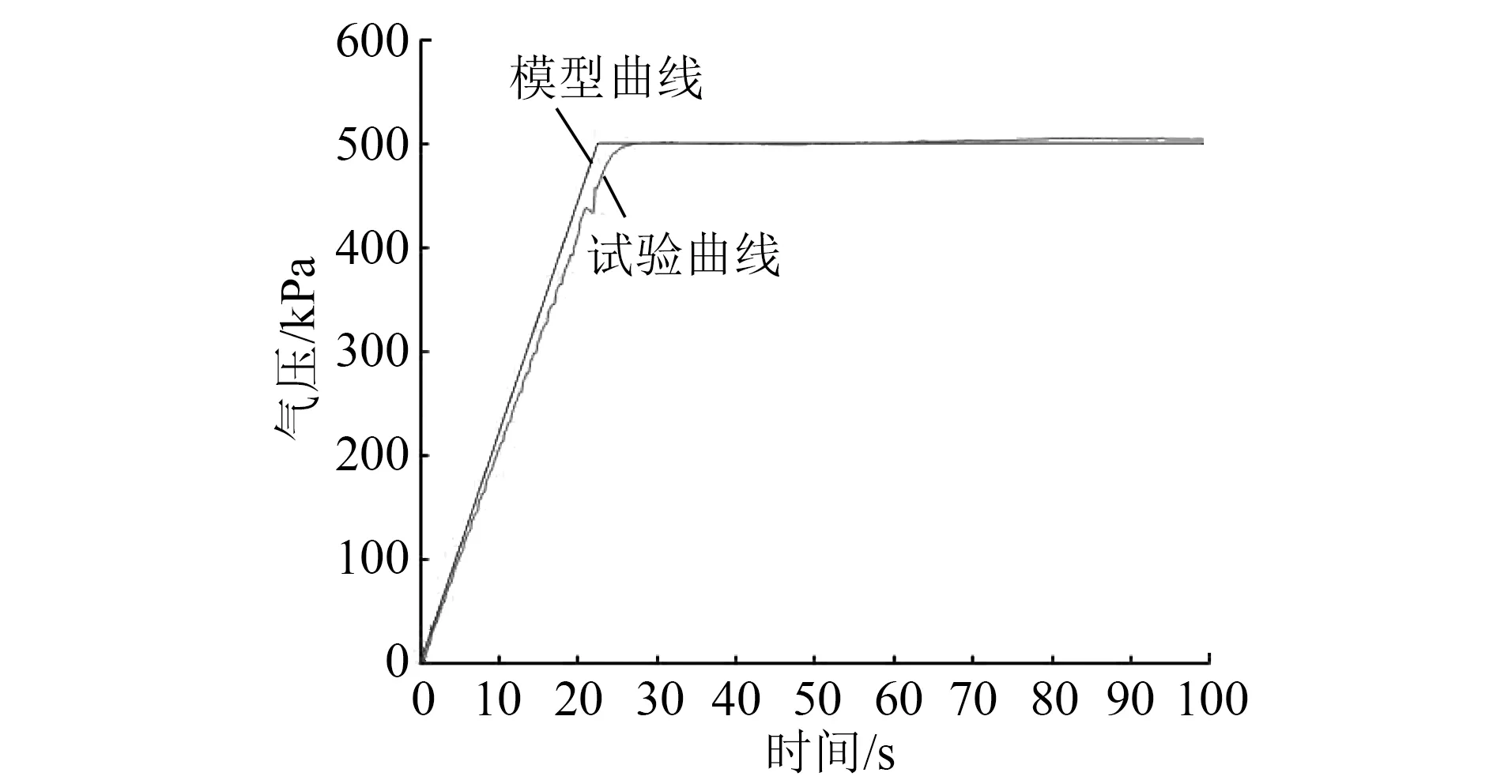
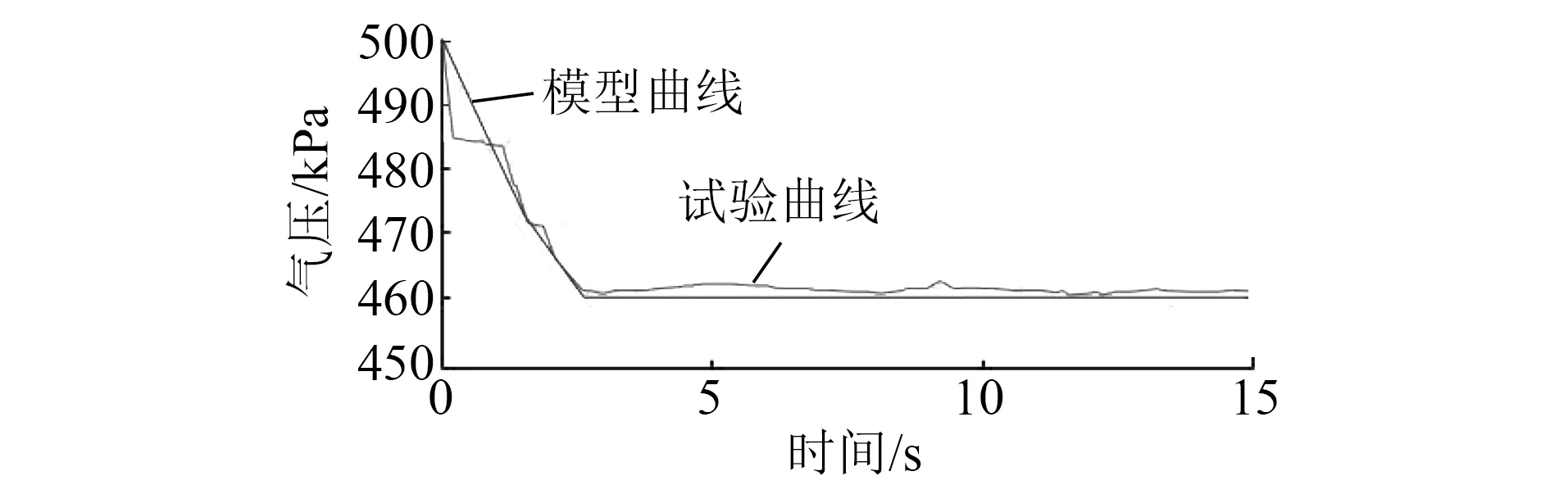
当5pa≤pl (3) 当pl0-r≤pl<5pa时, (4) 其中: (5) 式中: pl2——第2阶段局减结束后的列车管气压,kPa; r——列车管减压量,kPa; ω——空气波速,m/s,取336 m/s; t0——初始时间,s。 最终达到所需减压量时,列车管停止减压。此时,列车管内压力pl=pl0-r。根据以上数学模型,编制仿真程序,随着有效节流系数S值的确定,模拟不同编组列车一级制动工况下列车管内部不同位置气压变化状态。 列车管压力变化速率η的经验公式[11]为: (6) 式中: 将式(5)通过傅里叶级数展开,对照仿真和试验曲线曲率差异,以二次函数为气动系统流体方程式的修正函数,并以aex形式为基础函数对列车充放气数学模型进行修正。 为了验证以上模型的适用性,对单车制动系统(即N=1)列车管的初充气及制动过程气压变化分别进行了试验,结果如图6、图7所示。 图6 单车初充气列车管试验曲线 图7 单车一级制动列车管试验曲线 由图6可见,模型计算曲线与试验曲线几乎接近,两曲线的气压上升变化规律也大致相同,在25 s左右几乎同时到达500 kPa稳压状态。由图7可见,试验曲线一直在模型曲线上下一定范围内波动。所以可以得出结论,用容积充放气模型附加修正函数修正其他因素的影响,这一仿真试验方法对于近似模拟单车实际试验工况是可行的,这对于实现半实物仿真的实时性来说有着相当关键的作用。 建立了半实物仿真平台,通过虚拟的列车管数字模型控制实物列车制动系统进行初充气、制动及缓解。通过将传感器采集制动系统中列车管路及风缸上的气压数据,传入硬件控制系统中进行实时处理,验证上位机中虚拟的制动机数字模型,结合修正系数及因子对气动力学模型进行实时性精确修正。 本研究考虑的是用显性函数代替偏微分方程,结合列车管的制动波与缓解波传播规律,推导列车管容积充放气模型。该模型优势在于列车编组数量、气缸容积量可根据条件进行设置,并能准确得到相关的试验仿真结果。此解析法充分考虑了气体在管道内部压力变化规律,气体流动变化规律类似于指数函数,所以用指数函数aex反映主要列车管气压特征,以该函数为主导对模型进行修正。实际列车管制动或缓解过程中涉及的其它影响因素,通过进一步用特征函数来代替其产生的影响。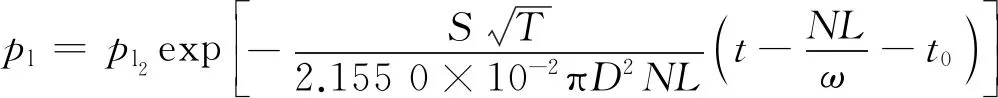
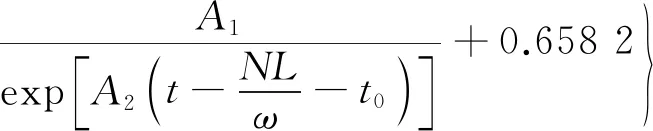
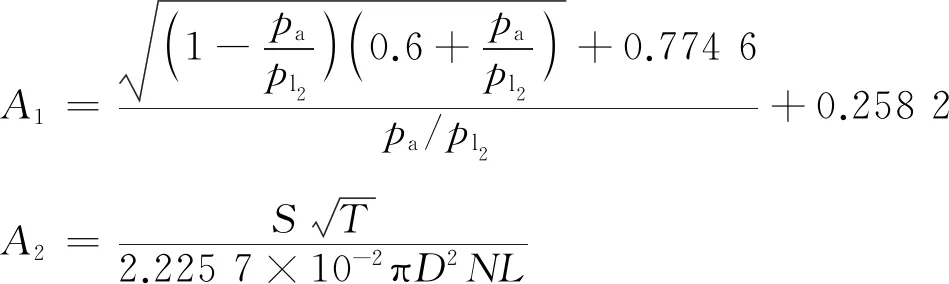
4 试验结果验证
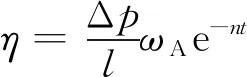
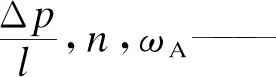
5 结语

