基于MIKE3流场模型的河流上游明渠弯道水流三维数值模拟研究

师于杰

(新疆维吾尔自治区塔里木河流域干流管理局，新疆 库尔勒 841000)

1 概 述

弯道中水流作曲线运动，在惯性离心力和水流自身重力的作用下，原有的水流结构遭到破坏，水流流态变得异常复杂[1]。这主要是因为多了一个离心力作用，使得水流流态失衡，产生凹岸高、凸岸低的水面横比降，并且由于上层水流流速大，受到的离心力大[2]。因此，在纵向流速和横向流速共同作用下，弯道水流呈表流指向凹岸、底流指向凸岸的螺旋流运动状态，在弯道环流的作用下，泥沙进行横向输移，导致弯道床底凹岸的冲刷、凸岸的淤积，造成弯道河床的横向比降[3]。明渠弯道水流运动主要的研究方向包括弯道水面横比降及超高、流速重分布、床面切应力、输沙特性及河床变形等方面[4]。

2 模型建立与工况

2.1 模型建立

DHIMIKE软件是专业的水力学软件，是经过大量的实际工程验证并且得到水力学研究人员广泛认同的商业软件。本文主要利用该软件中的水动力模块(HD)及泥沙输移模块(ST)。计算模型中，采用分层的网格，每一个网格单元均为三角形的棱柱体，即在垂直方向为矩形网格，水平方向为非结构三角形网格，分别对3种型式(圆弯道、缓圆缓弯道和对称凸型弯道)的弯道进行网格划分，见图1。

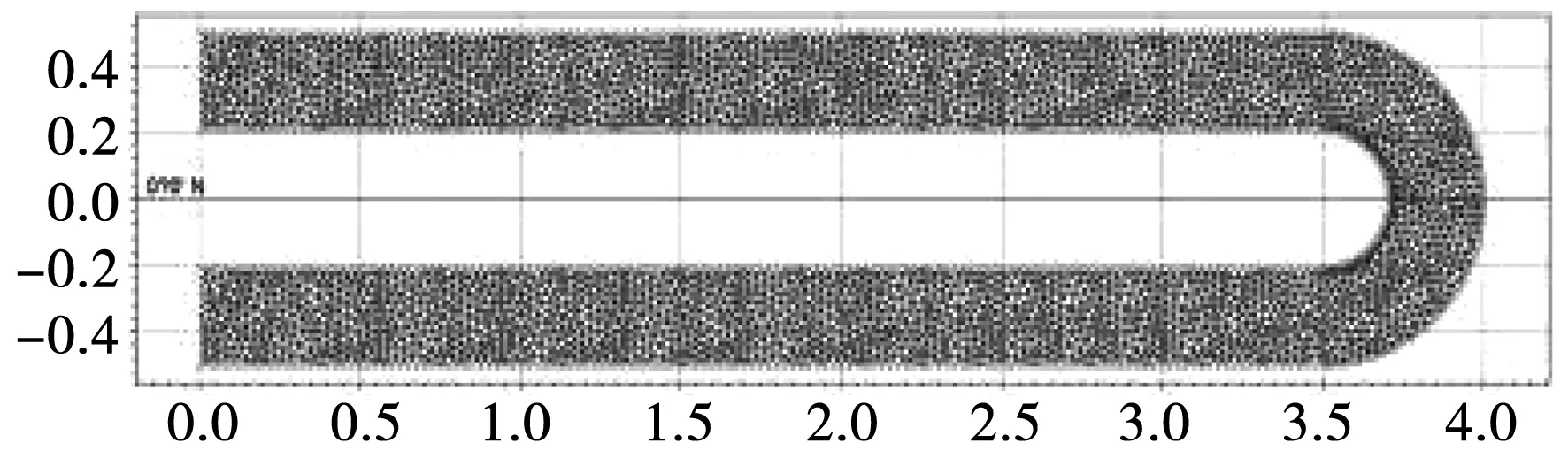
图1 模型计算图

2.2 清水定床模型工况

清水定床模型参数见表1。在计算过程中，固壁按照定边界条件进行计算处理。

表1 清水定床模型参数

2.3 清水冲刷模型工况

对于清水冲刷模型，首先在弯道底部进行铺沙，铺沙参数见表2。

表2 铺沙参数

将其他条件与清水定床模型的工况保持一致。在天然河道中，沙子的运动形式既有推移质也有悬移质，且泥沙一般为非均匀沙。在数值模拟计算时，想要实现混合粒径的泥沙颗粒以不同形态运动还是比较困难的，而且想要实现从上游补给推移质也有一定难度。在本文的清水冲刷模型中，弯道底部所铺沙子的粒径为0.22 mm，铺沙厚度为10 cm，进口水流为清水，需要考虑环流的影响。在计算过程中，对于弯道的几何形态，本文进行一定的简化处理，即边壁在计算中按照定边界进行处理，这样就只能定性地分析水流对堤脚、堤身的冲蚀破坏作用，并且局限于分析水流泥沙对河床的冲刷、淤积作用。

本文以圆弯道、缓圆缓弯道和对称凸型弯道为模拟计算对象，清水定床模型主要模拟水流流态及水面形态，通过HD模块模拟计算，模拟计算时间为1 h；清水冲刷模型主要模拟河床冲刷规律，通过ST模块模拟计算，取模拟时间为2 h。根据模拟结果图，绘制水流水面线图、流速图、环流图和河底冲淤趋势图等，定性对比分析3种典型弯道的水流形态及河床冲淤情况[5]。

3 数值模拟结果与分析

当水流由顺直河道进入弯曲河道时，在直道段的水流流过弯道处，由于轴线的曲率在弯道处的曲率难以适应，水流便会在此产生离心力，离心力的方向为指向凹岸，这样使得原有水流结构达到的平衡状态变得不平衡，由于水面的调整便会产生横比降。弯道处水面产生横比降后，会进一步引起弯道水流结构的调整。水流入弯之后产生的次生流与纵向主流叠加在一起，形成弯道特有的螺旋流，进而引起水流对堤身的冲蚀破坏及河床的冲淤变形。

3.1 水流结构变化分析

本文采用清水定床模型，在弯道水流流态稳定的情况下，分别对圆弯道、缓圆缓弯道和对称凸型弯道3种弯道状态进行对比分析。通过分析水面超高、比降以及平面流速的分布得到相应的结论。

3.1.1 水面超高和比降

对于水流的流向，当水流进入弯道后，不仅会受到水自身的重力作用，同时由于弯道的曲率、水流的流速方向发生改变，便会受到离心力的作用。所以，当水流的各个质点开始作离心运动时，弯道上的自由水面的平衡状态便开始发生改变，导致弯道处的凸岸水面低于凹岸水面，在弯道的横向自由面会形成具有一定倾斜程度的水面横比降。弯道水面超高的产生引起整个弯道水面形态的变化，进一步会引起弯道中水流结构的重新调整以及流速的重分布。见图2。

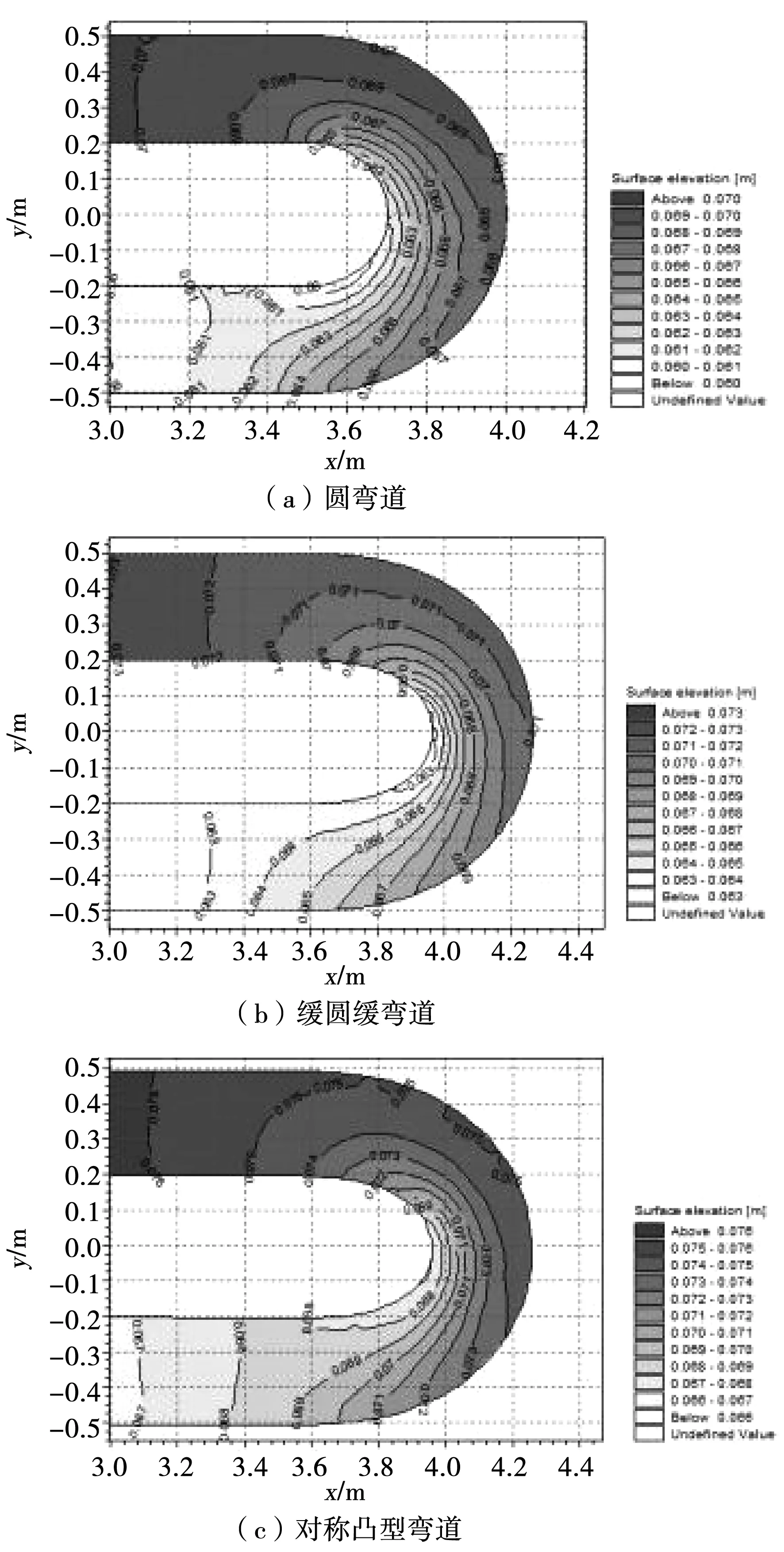
图2 弯道水位等值线图

图2为弯道的水位等值线图。从图2中可以看出3种弯道的水面形态有着相似之处：在弯道入口处，由于水流受到惯性影响，水位有雍高趋势；当弯道凹岸侧的水位逐渐壅高以后，在0°～90°断面的区域，水流动后，由于水流的流速产生的动能，将会转化为一定的势能，产生的结果会出现水位升高、流速减小的现象，此处的状态为高水位低流速区；当弯道的流动水流水位上升到最高时，由于水流受到惯性作用的影响，水位将会产生下降的趋势，此时由于势能转化为动能，即出现水位降低、流速增大的水流现象，也即低水位高流速区在90°～180°断面区域。

3.1.2 横比降纵向变化

3个典型纵剖面的水面线沿流程变化过程线见图3。

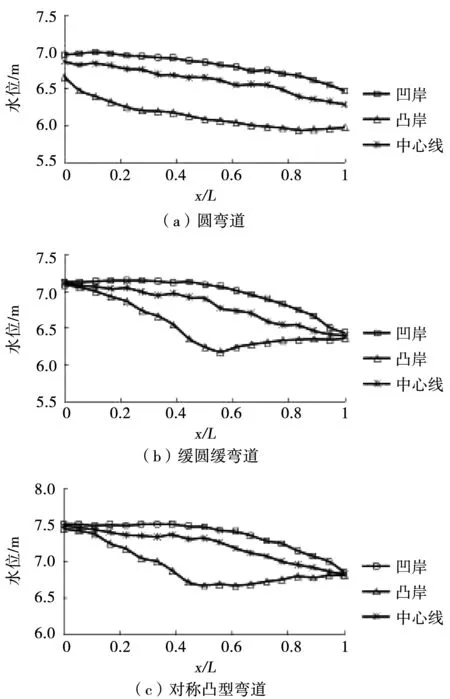
图3 弯道水面线沿程变化

由图3可知，这3种弯道水面线沿流程变化呈现的规律为：凹岸处的水面线、中心线水面线均呈上凸的曲线，凸岸水面线呈下凹曲线，且凸岸水面线较凹岸水面线变化更为激烈；弯道最大水位差一般会出现在弯顶断面附近，并向上下游两个方向逐渐减少；在弯道进口附近，缓圆缓弯道和对称凸型弯道的凹岸、凸岸及中心线的水面线较齐平，而圆弯道的3条水面线有水位差，表明在圆弯道进口断面前就有凹凸岸水位差发生；在弯道段，凸岸水位明显低于凹岸水位，而中心线水位界于两者之间；在弯道出口段，缓圆缓弯道和对称凸型弯道的凹岸、凸岸及中心线的水面线较齐平，而圆弯道的3条水面线有水位差，表明在圆弯道出口断面后凹凸岸还有水位差。以上情况表明，缓圆缓弯道和对称凸型弯道减少了发生水位差的弯道长度，其有效改善了弯道水面形态。

3.2 平面流速分布

通过得到不同水深处的U-V矢量图，分析弯道水流水平速度矢量在不同水深处的分布。本文选取3个水深，分别为z/h=1、0.5和0.1，所得到的结果见图4。

图4 圆弯道U-V矢量场

从图4中可以看出，3种弯道的水平速度矢量有相似的规律性：

1) 水深z/h=1处的速度值最大，水深z/h=0.1处的速度值最小。

2) 水流刚进入弯道时，各层水流流速表现为在靠凸岸侧流速增大，靠凹岸侧流速减小；水流经过弯道后，各层水流流速也一致表现为靠凹岸侧流速增大，靠凸岸侧流速减小。

3) 在弯道段，z/h=1处属于表面流层，其主流向明显偏向凹岸，在距离床面一定距离后，即z/h=0.5时，主流向近似与边界平行，z/h=0.1属于近底流层则明显偏向凸岸，表明弯道水流底部流向和表层流向交错的重要特征，产生了螺旋流运动；水流在弯道下游出口段逐渐趋向一致，与槽边平行。过去泥沙起动多用断面平均流速表示，事实上，近底流速对泥沙颗粒起动的影响最为重要。图5为3种弯道处的凹岸、凸岸和中心线的近底流速对比图。

图5 弯道近底表层流场图

通过图5的对比分析可知，缓圆缓弯道和对称凸型弯道的流速大小和变化范围基本相似。在凹岸处，近底流速小于圆弯道；在凸岸处，弯道进口附近及过弯顶断面后这两种弯道近底流速较圆弯道明显减小，表明插入缓变曲线后的弯道有效减少了过大、过小近底水流流速的出现，对壁岸、床底的淘刷程度将会小于圆弯道。

4 结 论

对圆弯道、缓圆缓弯道和对称凸型弯道水槽3种弯道的水面形态、水流流态及河床冲淤变形等进行数值模拟计算，然后对比分析，得出以下结果：

1) 插入缓变曲线的弯道可以明显改善边界对水流的约束力，有效改善水面形态，表现在可以有效改善除弯顶断面附近以外的水面超高、水面比降，但在弯顶附近的区域，改善水面形态效果不太理想。

2) 一般情况下，弯道有两个高流速区：一个出现在凸岸，从进口断面到弯顶断面之间；另一个出现在凹岸，大约从弯顶断面到出口断面及下游。位于凹岸出口下游附近的高流速区，将引起该位置的床面冲刷，形成冲刷部位。