利用多源数据建立GA-BP算法模型估算PM2.5的研究

胡娟 郑军 许文龙 邱玉珺 胡方超

(1 南京信息工程大学 环境科学与工程学院，南京 210044；2 南京信息工程大学 网络信息中心，南京 210044； 3 南京信息工程大学 大气物理学院，南京 210044；4 常州市环境科学研究院，江苏 常州 213022)

引 言

PM2.5是指悬浮在空中的空气动力学当量直径小于或等于2.5 μm的细颗粒物，严重影响环境、气候，甚至危害人体健康[1-2]。尽管环境监测站对近地面PM2.5直接测量的精度很高，但在监测样本点的数量与分布上有一定的局限性，难以反映PM2.5的时空变化，而利用遥感卫星测量则可对其进行大范围的区域监测。目前诸多研究是在卫星遥感反演产品AOD (Aerosol Optical Depth)的基础上对PM2.5质量浓度进行估计[3]。现今卫星探测传感器可为大气气溶胶监测提供数据产品，尤以MODIS的气溶胶光学厚度AOD L2产品Terra MOD04与Aqua MYD04为典型，因其反演算法成熟、产品质量可靠、时间连续性好，所以应用最为广泛[4]，特别是在大气环境监测领域。

利用卫星遥感技术对PM2.5进行长时间、大范围、高空间分辨率的监测也是当前大气污染治理的一项重要内容。已有研究表明，AOD与近地面PM2.5具有强相关性[5]，利用卫星估算近地面PM2.5质量浓度几乎都是基于AOD展开的[6]，主要有线性或多元回归模型[7-8]、地理加权回归及神经网络的高级统计模型[9-10]。一般而言，卫星AOD包括实际大气整层信息，需结合气象数据或再分析资料做相应的高度与湿度订正，这样与PM2.5的相关性更高。

由于PM2.5的时空变化会受到大气环境、气象、地理等诸多因素的影响，随着近年来机器学习技术的发展，已有学者利用BP(Back Propagation)神经网络[11]、随机森林RF(Random Forest)[12-14]、支持向量机SVM(Support Vector Machine)[15]等方法来估算中国东部PM2.5[16]。机器学习模型既不需详细了解大气污染的物理化学过程[17]，也不需对卫星遥感的机理进行更深入的研究，只要根据统计学原理，利用机器学习的特定算法即可。理论上，输入的信息越多，机器学习的效果越好。由于地面PM10包含PM2.5，两者明显正相关，且常常是通过AOD一起估算，而能见度(VIS)数据包括大气成分、相对湿度等多因素，其与PM10很少被用来估算PM2.5，但能见度也代表了近地面信息，与AOD联合可用来表示气溶胶的标高，但近年来已有研究在机器学习算法中应用VIS与PM10来估算PM2.5[14，18-19]。

因此，通过机器学习进行卫星遥感反演PM2.5是一种更具应用潜力的监测方法。基于遗传算法的GA-BP(Genetic Algorithm-Back Propagation)神经网络作为BP神经网络的发展，被用于估算PM2.5的研究还不多见[20]。本文尝试结合地面站点的气象、环境监测数据，通过GA-BP机器学习算法来训练表达卫星遥感反演得到的AOD与近地面PM2.5之间复杂的非线性关系，从而估计PM2.5的质量浓度。

1 数据来源及算法原理

1.1 研究区域

选取南京地区各站点所代表的区域作为研究区域，研究区域内的气象观测站点(简称气象站，下同)与环境监测站点(简称环保站，下同)分布如图1所示。在进行数据站点匹配处理时，按照最近距离原则，即每一个环保站总是要找到一个最近的气象站与之匹配对应。

图1 南京地面站点分布(单位：km)

1.2 数据来源

卫星遥感数据来自美国地球观测系统EOS(Earth Observation System)系列卫星上的Terra和Aqua卫星所携带的MODIS提供的Level 2产品数据AOD，上午为Terra MOD04_3 km， 下午为Aqua MYD04_3 km，地面分辨率均为3 km，每日上、下午各一次，可提取有关日期(Date)、经度(Lon，(°))、纬度(Lat，(°))及AOD等信息。

气象数据为中国地面气象站逐小时观测资料，包括日期(Date)、站号(Station_Id_C)、纬度(Lat，(°))、经度(Lon，(°))、气温(TEM，℃)、气压(PRS，hPa)、相对湿度(RHU，%)、2 min平均风向(角度)(WIN_D_Avg_2 min，(°))、2 min平均风速(WIN_ S_Avg_2 min，m·s-1)、能见度(VIS，m)、天气特征(WEP)。其中WEP表示测站所观测到的各种天气现象，变化范围从00～198。

国家环保部地面监测站点数据来自中国环境监测总站的全国城市空气质量实时发布平台，使用其逐小时空气质量数据，包括日期(Date)、PM2.5、PM10质量浓度等。

1.3 研究方法

1.3.1 BP神经网络工作原理

BP神经网络(Back Propagation neural network)由Rumelhart，et al[21]提出，在神经网络训练中引入了δ学习规则(用于调整各层神经元的权值和阈值的方法)，是一种按误差反向传播算法训练的多层前向反馈神经网络，由信息的正向传播和误差的反向传播两个过程组成。

正向传播过程指的是输入层各节点接收输入信息(如本文输入AOD、能见度、相对湿度、气温等)，并将信息传递给隐含层的各个节点，最后由输出层向外界输出信息处理结果(图2)。当实际输出与期望输出(本文输出为PM2.5质量浓度)没达到最小均方误差(Mean Square Error， MSE)条件时，则进入误差的反向传播，即误差通过输出层，按误差梯度下降的方式修正各层权值，向隐含层、输入层逐层再反向传递。就这样循环不断地调整各层权值和阈值，进行网络学习训练一直到MSE减少至可以接受的条件，或学习次数达到预设值为止。

图2 BP神经网络结构

由于BP神经网络中的初始权重和阈值一般是随机的，且梯度下降法的自变量范围被限制在单调区间内，这样容易导致陷入局部最优解而不是全局最优解，而且还存在学习收敛速度慢、泛化能力弱、存在欠拟合等缺陷[22]。

1.3.2 GA-BP网络算法

遗传算法(Genetic Algorithm，GA)是Holland[23]基于生物进化规律演变而得到的一种优化算法，它对复杂的、无明确关系的、多变量的、非线性的逼近效率较高，且能够按照适应度函数进行智能搜索以求得全局最优解。而遗传算法与BP神经网络相结合的GA-BP算法采用优化的初始化权值与阈值，能够在整个定义域内实现变量取值最大可能地接近全局最优解。

1.4 GA-BP优化算法建模

本文采用GA-BP算法结合MODIS AOD、地面气象站数据包括气温(℃)、气压(hPa)、相对湿度(%)、2 min平均风向(°)、2 min平均风速(m·s-1)、能见度(m)，以及地面环保站点PM10等数据建模估算地面PM2.5质量浓度(μg·m-3)。利用GA-BP神经网络训练，不断更新BP网络的权值和阈值直至满足条件判断并输出测试结果。GA-BP神经网络流程如图3所示。

图3 GA-BP神经网络流程

1.4.1 原始数据采集及时空匹配数据源(训练集和测试集)

其中，时空匹配站点，获取数据源包括：

(1)地面环保站点与气象站点时空匹配

将两者按时间和空间(站点经纬度最近距离)匹配，匹配后用经纬度标识(图1)。表1为匹配结果。选取六合、仪征两个气象站点，9个环保站点，其中5个用于训练，4个用于测试，如表1所示。

表1 国家环保站点与气象站点时空匹配数据

(2)地面站点与MODIS AOD时空匹配

表1中的中点经度、中点纬度是匹配后的环保站与气象站两站点之间中点的经纬度。对在此中点30 km范围内， 15 min时间内相应的MODIS AOD数据进行匹配，所用到的地表两点间(大圆)距离公式为：

L=Re×arccos[sin(lat1)sin(lat2)+cos(lat1)cos(lat2)cos(lon1-lon2)]

(1)

其中：地球半径Re=6 378.137 km；(lat1，lon1)、(lat2，lon2)分别为A、B两点的经纬度。

(3)PM2.5变量因子的相关性分析

不同时空范围内，AOD、PM10及气象条件因子和PM2.5质量浓度的相关性也存在差异，表2为对各站点某些变量因子与PM2.5作相关分析确定的网络输入层的特征因子。

表2 PM2.5与PM10、AOD和气象条件的相关性分析(相关系数R)

(4)确定输入变量组合试验

为了在模型中考查多源数据中地面数据的输入变量对卫星AOD输入变量的影响，构建了9个组合试验(表3)，分别用试验1，2，…，9表示。

表3 9组试验的各输入变量

1.4.2 GA-BP神经网络训练及仿真测试过程

在网络训练前首先要对样本数据统一进行归一化(Normalization)处理，然后随机选取样本进行网络训练，经过多次训练确定网络优化参数。将网络估算的PM2.5质量浓度和实际值的误差平方和的倒数作为遗传算法的个体适应度函数，通过选择、交叉、变异最终确定适应值最优的个体，即确定最优的权值和阈值并将其赋值于BP神经网络，再经过网络训练进行仿真测试，并将输出数据反归一化处理，得到网络模型估算的PM2.5。

1.4.3 BP及GA-BP模型性能评价

性能指标定义及公式，包括：

(1)决定系数(Coefficient of Determination)：

(2)

其中:E表示估算值;T表示实际值。

(2)相对误差(ei)、平均绝对误差(Mean Absolute Error， MAE)：

ei=|E-T|/T

(3)

(4)

(3)均方根误差(Root Mean Squared Error， RMSE)，用来衡量预测值与实际值之间的偏离程度：

(5)

(4)准确率(Accuracy)：把估算值的相对误差超过其实际值的20%视为不准确数据。

选取样本采用随机选取每个匹配站点数据的90%进行神经网络训练，并用匹配数据的10%进行仿真测试，并根据多次训练仿真测试保存训练最好的网络用于南京其他站点的验证试验，即在9个环保站中选用5个站点训练选出最好的网络来估算其他4个测试站点的PM2.5。

2 结果与讨论

2.1 影响PM2.5估计的各相关因子分析

以南京各站点为例进行分析，试验利用皮尔逊相关系数估计变量x、y间的相关。公式如下：

(6)

就南京地区2017年和2018年的数据分析来看(表2)，各变量因子与PM2.5相关性系数R按平均值大小依次为： PM10(0.771)、WEP(0.467)、PRS(0.312)、AOD(0.186)、WIN_D_Avg_2 min(0.061)、RHU(0.008)、WIN_S_Avg_2 min(-0.135)、TEM(-0.370)、VIS(-0.625)。从相关系数绝对值的大小划分相关强度，PM10、VIS为中度相关，WEP、PRS、TEM、AOD为低度相关，其他因子相关相对较弱。不同的年度、季节和月份相关性也存在一定的差别，同一站点PM10与PM2.5相关性，2017年要明显高于2018年。表2中WEP多数为无云、有雾或霾的情况，但由于2017年南京夏季WEP匹配后的数据全为0(表示未观测或观测不到云的发展)，故当训练模型采取分站点分季节训练时，不再考虑WEP作为变量因子，最多使用8个输入变量作为变量因子，如表3试验6所示。

由于受到匹配样品数量的限制，需要把数据分为同站点不同年度、不同季节进行网络训练、仿真测试和验证试验。

2.2 BP与GA-BP网络模型性能比较

2.2.1 BP网络与GA-BP网络训练性能指标评价结果比较

对南京各环保站和气象站按最近空间距离匹配，站点匹配结果并按“环保站_气象站”的格式来表示。匹配后的网络训练站点(5组)分别为：迈皋桥_仪征、玄武湖_仪征、草场门_六合、瑞金路_仪征、中华门_六合。匹配后的试验测试站点(4组)分别为：山西路_六合、浦口_六合、奥体中心_六合、仙林大学城_仪征。

在输入数据中使用“试验6”的变量组合，对BP与GA-BP的训练结果比较见表4，可以看出，GA-BP整体上比BP(除了春季外)性能表现优越。尽管在春季时，BP表现较GA-BP好，但在其他大量试验中，春季的BP常出现比GA-BP表现欠佳的情况。

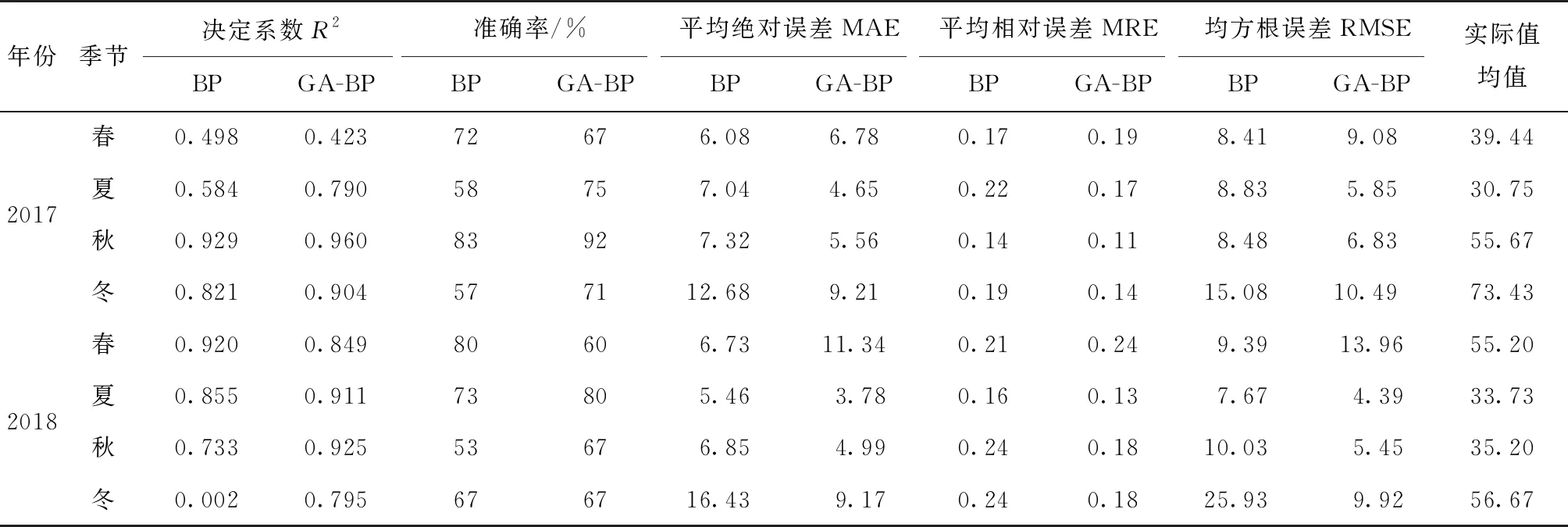
表4 BP与GA-BP网络训练及仿真测试的主要性能评价指标值

2.2.2 网络训练及仿真测试效果

同上也选择试验6组合，对BP网络和GA-BP网络预测样本的估算值与实际值进行比较，分析两个网络的训练及仿真测试的效果，如图4所示。可以看出，2018年除了春季外，其他3个季节GA-BP的R2与RMSE表现均较BP好，尤其是夏秋两季，特别是在冬季匹配数据很少的情况下，BP几乎不能起到估计的作用，而GA-BP网络R2与RMSE的表现，其优势则比较明显。故下文就采用GA-BP网络设计做进一步的试验。

图4 2018年南京匹配站点样本BP与GA-BP估算PM2.5结果对比：(a)春季；(b)夏季；(c)秋季；(d)冬季

2.2.3 试验1—9结果比较

图5a、b可以看出，从试验1到试验5，每组试验均增加一个变量因子，每增加一个变量因子时，对输出PM2.5的R2与RMSE，其影响是不同的。在1—6组试验中，与其他5组试验相比，试验1中AOD的R2较小，RMSE较大。这主要是因为AOD表征的是大气整层的气溶胶的影响，而其他变量因子均是在近地面几个参数的测量，均一定程度上反映了近地面的信息，所以与PM2.5有着更好的相关性。在试验2—5中，由于变量因子PM10的加入，各个季节试验2中R2较试验1有大幅度地增加，而在春季试验5中由于TEM的加入使R2较试验4略有下降；在秋季由于PRS(气压)加入，试验3中R2较试验2也略有下降；在春季试验4中VIS的加入，较试验3 2018年的R2增加较大，而2017年时的R2却略有降低；在试验6中，除了2017年秋季，加入相对湿度与平均风速、平均风向后，R2均有所增加。作为试验1—6的对照试验，增加了试验7—9，分别考虑没有VIS与PM10及两者都没有的情况。但从试验7—9的仿真测试的效果看，对比试验6，除了2017年秋冬季R2略有增大外，其他季节大多是R2减小RMSE增大。

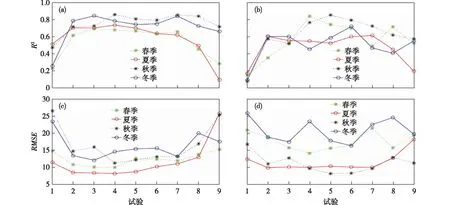
图5 南京站点9组试验各季节R2与RMSE的变化：(a)2017年R2；(b)2018年R2；(c)2017年RMSE；(d)2018年RMSE

总体来看，对于RMSE几乎都随着R2的增大而减小。四季中秋季相关性最高，2017年的R2与RMSE总体要好于2018年，而且在9组试验中试验6总体也表现较好。

以仙林大学城_仪征的匹配站点为例，仅选用了试验1与试验6进行比较，如图6所示。可知， 图6A、C为试验1， 图6B、D为试验6 ，2017年的R2与RMSE均是试验6较好；四季表现为秋季>冬季>夏季>春季，秋季R2最大为0.91，RMSE=11.79;春季最小R2=0.65，RMSE=8.67。而图6C、D分别为2018年试验1与试验6分季节情况，2018年的R2与RMSE也是试验6较好，但四季表现为秋季>春季>冬季>夏季，秋季的最大R2=0.87，RMSE=7.50;夏季最小R2=0.56，RMSE=6.46。总体上看2018年R2虽较2017年小，但RMSE也较小。

图6 仙林大学城_仪征站点试验1 (A：2017；C：2018)与试验6(B：2017；D：2018)网络测试效果(a—d分别为春夏秋冬；横坐标为估算样本的时间序列)

图5、6均表明，试验6的效果总体上要较前面试验表现较好，这是因为，对GA-BP而言，输入相关的变量因子越多，用于网络学习的信息就越多，对诸多变量因子所组成的非线性关系就表达的越好，对PM2.5的估计效果也较明显。

3 结论

(1)在有足够数据样本的情况下，不同季节的表现有时差别很大，需要进行分季节考虑。

(2)影响PM2.5估计的多源数据的各输入变量因子中，PM10与VIS(能见度)变量为相对高相关因子，其他输入变量 PRS(气压)、TEM(气温)、AOD等为低度相关，并在此基础上构建了9组基于卫星AOD作为基本输入变量的多源数据分季节估算PM2.5的试验，试验6的整体表现较好。

(3)利用GA-BP算法估计PM2.5比BP算法总体表现较好，所建立的多源数据GA-BP算法模型也为估算PM2.5的提供了一种新的机器学习的方法。