含导热块封闭方腔自然对流格子玻尔兹曼模拟研究

郑竟波 杨伟林 陈 磐* 韩 奎 廉正阳 倪 虎

(南京工程学院能源与动力工程学院,江苏 南京211167)

封闭方腔自然对流现象广泛存在于太阳能集热器的集热过程、温室型太阳房的设计、电子元件的散热、双层玻璃窗的生产等[1-3]工业领域中，是传热与流动学科中的一个经典问题，具有广阔的实际应用背景。在方腔自然对流这一问题中，速度场和温度场相互耦合，流动情况比较复杂，可呈现不同的流动结构，因此，对方腔内部的流动及传热问题的研究一直是各国学者普遍关注的研究热点。

至今为止已有不少研究者致力于研究封闭腔体内的自然对流特性，由于其影响因素繁多，机理复杂，故研究者们都力求一种更为高效的数值计算方法。基于分子动理论的格子玻尔兹曼方法[4，5]由于其清晰的物理背景、高效的并行效率及算法简单等优异特征，近年来受到越来越多的关注，并在自然对流流动换热领域得到了很好的应用。如王立海[6]采用格子Boltzmann方法研究了方腔内自然对流换热问题，并对该换热现象进行了理论分析。董长青[7]以压力分布函数和内能密度分布函数为演化变量，构建了新的双分布热格子Boltzmann模型，对封闭方腔内自然对流进行了数值研究。曹先齐等[8]采用格子Boltzmann方法构建了非稳态方腔自然对流的数学模型，并进行模型验证，重点讨论了瑞利数R a、倾斜角度θ对方腔内非稳态流动特性和传热特性的影响。文献[9]采用格子Boltzmann方法，分析研究侧壁面为正弦温度分布条件下的方腔自然对流，并研究了瑞利数以及高宽比变化时其对腔体流线分布和等温线分布的影响规律。文献[10]采用格子Boltzmann方法对倾斜二维封闭方腔自然对流换热进行研究，重点讨论了倾斜角对自然对流换热的影响。文献[11]用格子Boltzmann方法对方腔内二维多孔介质自然对流传热问题进行了研究，并详细讨论了孔隙度及孔隙度变化时其对自然对流传热的影响。文献[12]另辟蹊径，应用格子Boltzmann方法（LBM）研究了三角形腔内的水的自然流动问题，分析了不同瑞利数和三角形方腔倾角对流场和温度场的影响规律。文献[13]采用格子Boltzmann方法研究了多孔介质方腔底部局部加热的自然对流传热，主要分析了高温热源位置及尺寸对流场、温度场的影响规律。

然相比于封闭方腔自然对流问题，实际工程应用中的方腔结构更为复杂，方腔中含有导热块更是非常普遍的情况，因此，本文以内含导热体的方腔自然对流为研究对象，采用格子玻尔兹曼方法，以探讨瑞利数、导热块大小及位置等因素对方腔自然对流流动规律的影响，分析自然对流过程中的流场特性和温度分布规律，以期获得对带有导热块的方腔自然对流研究及相似领域研究提供有益参考。

1 问题描述及控制方程

方腔内含导热块自然对流的物理模型如图1所示。腔体的水平宽度为L，垂直高度为H，腔体高宽比K=H/L=1.0 。腔体左侧壁面为高温壁面，温度为Th，右侧壁面为低温壁面，温度为Tc，上下壁面绝热边界。在腔体内部正中心处有一正方形导热固体块，其宽度为W。模拟时假设导热块的热扩散系数与腔内介质热扩散系数相同。

图1 自然对流示意图

宏观控制方程如下：

方程（1-4）中u、T、ρ、p、v、λ、cp、β、Tref、t分别为宏观速度、温度、密度、压力、运动粘性系数、导热系数、比热、热膨胀系数、参考温度、时间。

控制输运过程的无量纲准则数是普朗特数Pr和瑞利数Ra，分别为：

式中a、ΔT为热扩散系数、特征温度差。

2 格子Boltzma nn方程模型

采用基于Boussinesq假设的耦合双分布函数模型来模拟封闭方腔自然对流[14]，速度场和温度场的耦合通过速度分布函数演化方程中增加一外力项来实现。其速度场和温度场分布函数分别为：

式（6-7）中r为空间矢量位置，t为时间，ei为格子离散速度，Δt为时间步长，т、тT为无量纲松弛时间，fieq、gieq、Fi为平衡态速度分布函数、平衡态温度分布函数和外力项，其表达式分别为：

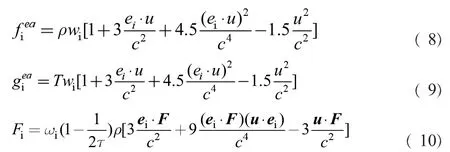
式中wi为权系数，ρ密度，格子速度c=Δx/Δt，Δx为格子步长。

宏观密度和速度可计算如下：

松弛时间系数т、тT

采用非平衡外推方法[15]进行固体壁面速度边界的处理，其整体精度为2阶，具有较好的数值稳定性。

式中rw代表边界上的点，rn位离边界点最近一个内部点。

3 模拟结果讨论

3.1 模型验证

图2为方腔内不含导热块的流线图和等温线图。从图2（a）可以看出，瑞利数Ra为103时，流动的特点是方腔中央出现一个近似圆形的涡，而在图2（b）等温线图中，瑞利数Ra为103时其等温线近似垂直。这与文献[6,7,15]的计算结果基本一致。为了进一步验证模型的准确性，还将本文获得的方腔中央涡的位置与文献[6，7，15]中的涡位置进行比较，其涡位置也基本一致，见表1所示。说明本文构建的格子Boltzmann模拟程序是可靠的。

图2 瑞利数Ra=103时,方腔内不含导热块时流线图和等温线图

表1 自然对流涡的位置(Ra=103)

3.2 瑞利数Ra数的影响

图3-4展示了方腔内含导热块自然对流在不同Ra数下流动稳定后的流线、等温线变化趋势图，其中固体块宽度W=H/3。对于流线图，由图可以看出，随着瑞利数Ra的变化，其流线变化显著。当Ra数较小（Ra=103）时，其流线表现为绕着中心导热块的多层同心圆。当瑞利数增加至105时，在导热块左右附近出现了两个涡。当Ra=106时，浮升力增加，竖壁边界层的作用也大大增加，因而涡的卷起作用增强，在导热块左右附近产生的两个涡偏离方腔中心的导热块，分别向左上壁面和右下壁面移动，且两个涡都分别出现了两个次级涡。

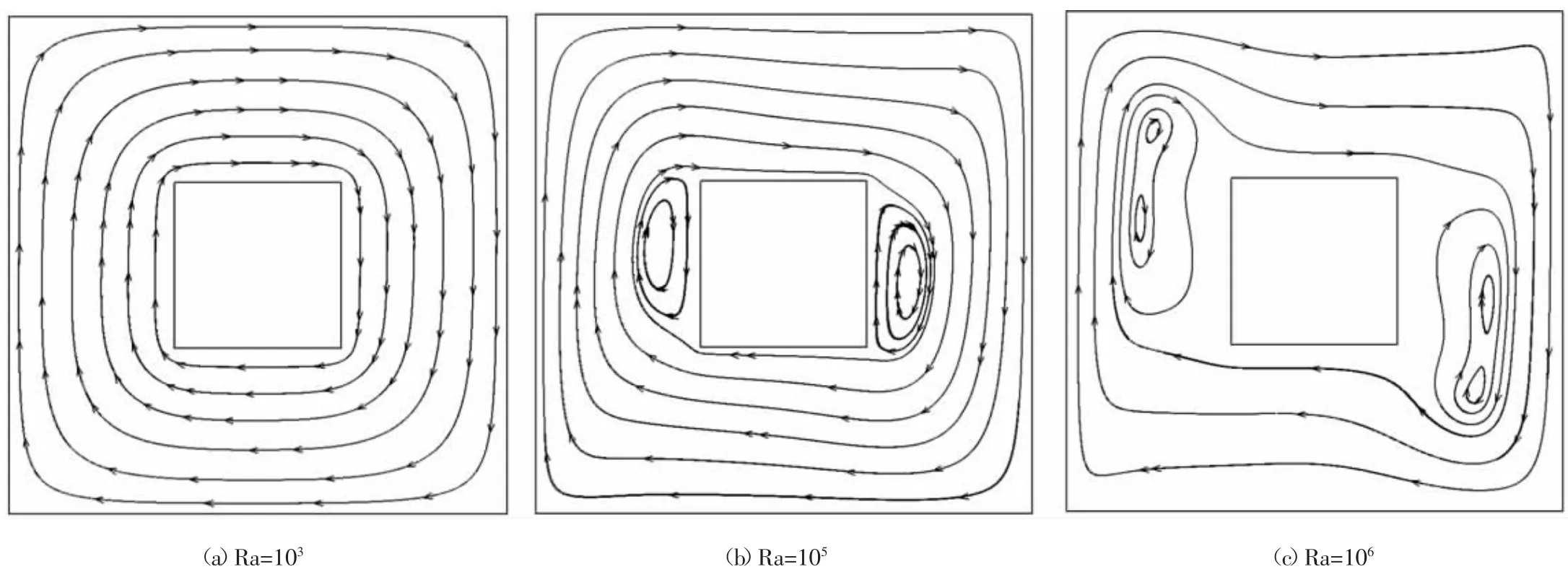
图3 不同瑞利数下流线分布情况

对于等温线图，在Ra数较小（Ra=103）时，观察图4（a）等温线图，可知其等温线几乎是垂直的，表明在瑞利数偏低时冷热壁之间的传热主要由热传导引起的，即热传导占主要地位；观察图4（b）-（c）等温线图，随着瑞利数Ra不断增加，等温线在方腔中央近似呈水平分布，而热壁面和冷壁面的等温线保持垂直，且越来越密集，形成一层薄边界层，说明腔体内对流加剧，热传导逐渐减弱，对流占据主导地位。其中，由于固体块位于方腔中央，且模拟时假设固体块的热扩散系数和腔体内介质一致，因此腔体内加入导热块和无导热块时其等温线区别不大。

图4 不同瑞利数下等温线分布情况

3.3 导热块宽度W的影响

图5-6展示了不同导热块宽度下的流线、等温线变化趋势图，其中Ra数固定为106。对于流线图的变化，对比图3（c）和图5（a）-（c）,可以看出，导热块宽度W比较大（W=0.6 H）时，在左右两侧高低温壁面条件作用下，形成了一个绕导体块的大涡流，且从图5（a）还可发现在导体块左右附近的两个次级涡。当W减小至H/3时，固体块附近的两个次级涡向左上和右下移动，且分别又产生了两个三级涡，见图3（c）。随着W的继续减小，流线变得不规则，左右两侧的两个三级涡其中一个逐渐消失。当W减小至H/15时，在固体块左右分裂出两个小涡。

图5 不同导热块宽度时流线分布情况

对于等温线图，对比图4（c）和图6,可以看出，随着W的减小，其等温线没有显著区别。只有在W特别大时，其水平分布的区域比较大一些，也更平直一些，见图6（a）所示。

图6 不同导热块宽度时等温线分布情况

3.4 导热块在方腔内位置的影响

图6-7展示了导热块在方腔不同位置下的流线、等温线变化趋势图，其中Ra数固定为106。对于流线图的变化，对比图3（c）和图7,可以发现，导热块在方腔不同位置，其流线变化显著不同。当导热块位于方腔上部时，方腔右下部靠近低温壁面处出现一个涡心，包含两个小涡。当导热块位于方腔下部时，涡心则在方腔左上部靠近高温壁面出现。另外，导热块偏上或者偏下，由于导热块的存在，流线在导热块附近都发生了扭曲。

图7 导热块在方腔位置不同时流线分布情况

对于等温线图，对比图4（c）和图8，可以发现，当导热块位置偏上或者偏下时，方腔中部等温线水平分布区域减小，导热块区域等温线倾斜分布，热壁面和冷壁面等温线保持垂直，形成的薄边界层仍相同，没有发生变化。

图8 导热块在方腔位置不同时等温线分布情况

4 结论

本文建立了内含导热块的方腔自然对流格子Boltzmann方程模型并进行了数值模拟，重点分析了不同瑞利数Ra和导热块宽度及位置对腔体流线分布和温度分布的影响，具体结论如下：

4.1 随着瑞利数的增加，在导热块左右位置处出现两个次级涡，随着瑞利数的继续增加，导热块附近的两个涡分别向左上、右下移动，且两个次级涡都又分裂出两个三级涡。

4.2 不同的导热块大小对腔体内流体流型影响较大。当腔内导热块比较大时，形成了绕导体块的大涡流，以及导体块左右附近的两个次级涡，流线比较规则。随着导热块宽度减小，流线变得不规则，腔内漩涡的数量增加。

4.3 改变瑞利数及导热块大小其温度场与不含导热块方腔自然对流的温度场相比，区别不大。

4.4 导热块位置对腔内流型及温度场影响都比较大。当导热块位于方腔上部时，方腔右下部靠近低温壁面处出现一个涡心。当导热块位于方腔下部时，涡心则在方腔左上部靠近高温壁面出现。当导热块位置偏上或者偏下时，等温线在导热块区域是倾斜分布的。