3-RHUR/PUS+PP混联机器人构型与性能分析

田 昕 赵铁石 王 唱 李二伟 盛 煜

(1.燕山大学河北省并联机器人与机电系统实验室， 秦皇岛 066004；2.燕山大学先进锻压成形技术与科学教育部重点实验室， 秦皇岛 066004)

0 引言

与串联机构相比，并联机构具有结构紧凑、刚度高、承载能力大等优点，因此有关学者对此进行了广泛研究[1-5]。但并联机构工作空间相对较小，串并混联机构可以结合串联机构和并联机构的优点，更易满足机器人工作空间和高刚度的综合性能需求。Tricept系列[6-7]和Exechon系列[8]机器人以及TriVariant混联机械手[9-10]等，通过采用两转一移三自由度并联机构串联两自由度摆头的混联形式，取得了良好效果。但由于工作空间小、双摆头结构复杂和制造精度要求高等原因，影响了其推广使用。采用并联头串联移动导轨形式的混联机器人，如搭载3-PRS 机构的ECOSPEED系列混联机器人[11-12]，其自身刚度更易保障，且易获得导轨移动方向更大的工作空间。由于3-PRS 机构工作空间与RS铰链间连杆长度成正相关，影响了其大工作空间的刚度性能。TIAN等[13]提出了四自由度并联头串联移动导轨的五自由度机器人构型，但由于并联机构的限制，其Y方向移动量很小，只适用于该方向小范围移动的情况。

在提升机器人综合性能方面，LIU等[14-15]提出了运动/力传递性能指标，并对3-PRS并联机构进行了优化和尺寸设计。ZHANG等[16]采用遗传算法对球形机构的全局条件数和工作空间进行了优化。ZHANG等[17]采用差分进化算法对3-UPU并联机构的刚度和可达工作空间进行了优化。文献[18]考虑机构的动力学性能、速度性能和刚度性能，采用改进的加权求和法进行了多目标优化。文献[19]根据工作空间与力传递效率性能指标对五自由度混联机器人R(2RPR)R/SP+RR进行了尺寸优化。文献[20]建立了2-PUR-PSR并联机构尺度综合多目标优化数学模型，并验证了MPSO算法的有效性。

为进一步提升串并混联机器人大行程刚度等综合性能，本文提出一种带随动滑筒的3-RHUR/PUS并联头串联XY双导轨的混联五自由度机器人构型，对其位姿及运动学进行分析，研究混联机器人的方向刚度，并采用OptLHS采样与三次插值结合的算法对混联机器人进行多目标优化。

1 五自由度混联机器人

1.1 机器人构型

本文提出的3-RHUR/PUS并联头串联XY双导轨机构如图1所示。

串联双导轨方向与并联头驱动H副轴线方向两两互相垂直。如图2所示，并联头包含3条RHUR驱动分支和1条PUS随动分支，其螺旋副(H副)和移动副(P副)平行固定于并联头基座，H副沿半径为R的圆周均匀布置，由各分支第一转动副(R副)驱动，P副过该圆中心。为了保证并联头大行程刚度，避免H副伸出杆大行程时对机器人性能的影响，该中间PUS随动分支的P副设计为随动滑筒结构，为3条RHUR驱动分支的H副提供大行程移动支撑，从而解决了并联头刚度精度降低问题。H副通过万向铰(U副)连接长度为L的连杆，连杆另一端与并联头动平台通过第二转动副连接。随动分支连杆通过U副和球副(S副)分别连接随动分支P副和并联头动平台。动平台上3个第二转动副沿圆周均布，半径为r，S副位于该圆圆心。并联头连接及尺寸关系如图3所示。

1.2 机器人自由度

据修正的G-K公式[21]计算3-RHUR/PUS空间机构的自由度为

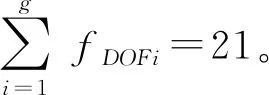
五自由度混联机器人为并联头串联双移动导轨形成的3-RHUR/PUS+PP混联机构。该3-RHUR/PUS+PP机器人具有沿X、Y、Z轴移动和绕X、Y轴转动自由度。

2 运动学与刚度

2.1 混联机器人位置正反解

建立包含工件坐标系{W}、混联机器人基坐标系{B}、并联头基坐标系{F}以及并联头动平台坐标系{M}4个坐标系的坐标系系统，如图1所示。其中，工件坐标系{W}、基坐标系{B}与定系{F}仅存在平移而无方位改变，其相对关系可表示为

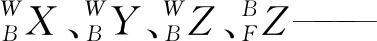
并联头动平台坐标系称动系{M}。坐标系固定于并联头动平台，原点M位于S副圆心，初始位置时，坐标轴方向与工件坐标系{W}、基坐标系{B}、定系{F}均一致，其X轴始终过第一分支上平台转动铰链点A1。

采用偏转角θ和方位角φ对末端执行器进行描述，可更清晰地表达其方向，令末端点到机器人方向为其正方向，其方向向量为

n=[sinθcosφsinθsinφcosθ]T

且θ∈[0°,90°]，φ∈[0°,360°]。

由于工件坐标系{W}、基坐标系{B}与定系{F}方位完全一致，3-RHUR/PUS三自由度并联机构的运动姿态在3个坐标系中的表达相同。且动系{M}的Z轴方向向量与刀具方向向量相同，满足nz=n。采用ZYZ欧拉角对动系{M}姿态进行描述，其旋转变换矩阵为

假设末端点T在工件坐标系{W}中的位姿参数为

T=(WTx，WTy，WTz，φ，θ)

其中，WT=[WTxWTyWTz]T为末端点T在工件坐标系{W}中坐标位置参数，由此易知末端点T在基坐标系{B}中的坐标为BT。令末端点T到动系{M}原点的距离为Lt，可得动系{M}原点在基坐标系{B}的坐标为BM，在定系{F}中的坐标为FM。

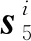
第i分支U副绕H副轴线转动角，即丝母被动转动量

若H副节距为Pd，则并联头转动驱动Ri为

根据连杆长度L恒定，并由转动副运动特性知，连杆方向始终与分支第二转动副轴线方向垂直，建立约束方程

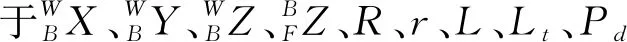
FMx=BMx-Px
FMy=BMy-Py

同理，该混联机器人由驱动到末端的正解位姿亦可求得，将5个驱动参数q=[R1R2R3PxPy]T作为输入，由6个非线性约束方程组可解得T的5个末端参数及转角ψ。

2.2 混联机器人速度与加速度

末端点在工件坐标系{W}的速度VT和加速度AT为包含角速度ωT=[ωTxωTyωTz]T、线速度vT=[vTxvTyvTz]T和角加速度εT=[εTxεTyεTz]T、线加速度aT=[aTxaTyaTz]T的六维速度矢量，且末端角速度ωT和角加速度εT与ZYZ欧拉角速度的关系为

式中sφ表示sinφ，cφ表示cosφ，sθ表示sinθ，cθ表示cosθ。

因此，末端在工件坐标系{W}的旋量速度WVT和旋量加速度WAT为

其中

WωT=wTWvT=vT-wT×WT

WεT=εT
WaT=aT-ωT×WT-ωT×(ωT×WT)

在整个混联机器人系统中，末端在工件坐标系{W}和基坐标系{B}的旋量速度WVT、BVT和旋量加速度WAT、BAT满足

(1)

(2)

(3)

(4)

其中

式中BVTF——末端点相对于并联头定系{F}在基坐标系{B}的旋量速度

FVTF、FATF——末端点相对于并联头定系{F}在定系{F}的旋量速度和旋量加速度

BVF、BAF——并联头相对机器人基坐标系{B}在基坐标系{B}的旋量速度和旋量加速度

在定系{F}中并联头各关节的运动螺旋表示为

第i(i=1,2,3)驱动分支各关节到末端的速度和加速度映射关系为

其中

其逆解为

(5)

(6)

其中

定系{F}相对于基坐标系{B}的运动只有X和Y导轨的移动，并无转动及沿Z方向的移动，因此并联头相对于基坐标系{B}的旋量速度BVF和旋量加速度BAF为

(7)

其中BωF=[0 0 0]T

(8)

其中

求逆得

其中

综上可得，串并混联机器人正逆运动学映射关系为

其中

q=[R1R2R3PxPy]T=qH(1:3,5,6)

2.3 混联机器人机构刚度

对该混联机器人而言，如连杆、关节连接件等相对于传动及伺服系统的变形可忽略，因此着重研究混联机器人的机构刚度，即只考虑驱动关节的变形对机器人的影响。少自由度机构在无自由度方向上无变形产生，该混联机器人不具有绕Z轴的转动，其绕Z方向的转动刚度为无穷大，本文利用其柔度矩阵分析该机构的方向刚度[23-25]。

令Kq=diag(kq1,kq2,kq3,kq4,kq5)，kqi为各驱动关节的刚度系数，则关节处变形与受力的关系为

τ=Kqdq

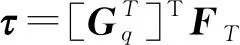
混联机器人末端位移与受力之间的关系为

D=CFT

令机器人末端所受外力为δF=δFf，且f为方向向量，则在f方向上，混联机器人刚度为

当f=[0t]T时，可得混联机器人移动的方向刚度，当f=[r0]T时，可得混联机器人转动的方向刚度。

3 尺寸优化

3.1 优化指标

(1)转动能力指标θm

该3-RHUR/PUS+PP混联机器人工作空间约束条件主要包含各驱动器的行程及并联头各关节的运动限制。关节限制如图5所示，上平台与连杆夹角即向量PBiAi与向量PMAi的夹角α满足α∈[20°,160°]，连杆与并联头Z方向即向量FPBiAi与[0 0 1]T夹角β满足β>100°，上平台转动副R2与并联头Z方向夹角，即向量FR2i与[0 0 1]T夹角γ满足γ∈[40°,140°]。

由于混联机器人驱动均沿坐标系方向，易知该机器人工作空间为长宽高为X、Y导轨与H副移动量的长方体空间与3-RHUR/PUS并联头产生伴随移动的并集。除了H副处于极限位置及其附近时，并联头运动产生的转动和伴随运动都一致。考虑机器人的实际应用需求，极限位置处产生的伴随移动并不能满足需求，其实际工作空间为长宽高为X、Y导轨与H副驱动移动量的长方体空间。

由于该构型混联机器人的转动自由度全部由并联头决定，为实现机器人的五自由度工作，其转动能力是优化中需要重点考虑的因素。规定刀具方向(即动系{M}Z轴)与基坐标系{B}Z轴方向的夹角为并联头偏转角，以可以实现的最大偏转角θ来衡量机器人的转动能力。

θm为可实现绕Z轴360°转动的最大偏转角。

(2)力传递性能指标Γ

为保证机器人在其工作范围内稳定的力传递，建立并联头的全局力传递性能指标，采用并联机构分支传动角对全局力传递性能指标进行分析。

并联头驱动三分支沿圆周均匀布置，其传动角可表示为∠MAiBi(i=1,2,3)或其补角，如图6所示。

为保证机器人在其工作范围内稳定的力传递，建立机构的全局力传递性能指标为

χi=sinμi为局部力传递性能指标，μi为3-HRUR/PUS并联机构单分支传动角。且Γ∈(0，1)，取值越大，机器人的力传递性能越好。

(3)速度性能指标κ

选取速度雅可比矩阵的条件数在工作空间的全局值κ作为全局速度性能指标计算式为

式中kmax、kmin——混联机器人速度雅可比矩阵奇异值的最大值和最小值

κ∈[1，∞)，越接近于1，机器人的速度各向同性越好。

(4)刚度性能指标σ

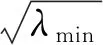
3.2 目标函数

通过上述分析，利用线性加权组合法，对全局转动能力指标θm、全局力传递性能指标Γ、全局速度性能指标κ和全局刚度性能指标σ进行综合考虑，实现混联机器人的多目标优化。

将上述优化指标的目标函数分别表示为

式中 Min()、Max()——不同指标在参数变化范围内的最小值和最大值

综合考虑4个指标的影响，建立混联机器人多目标综合优化函数

式中τj——优化指标权重系数

3.3 优化步骤

3-HRUR/PUS+PP混联机器人，从自由度考虑，绕X、Y轴的转动自由度由3-HRUR/PUS并联头产生，完全受并联头各关节相对位置的影响；X、Y、Z轴3个方向的移动，由于驱动方向均沿X、Y、Z轴方向，因此可直接根据需求选择满足要求的驱动。综上所述，该混联机器人尺寸优化确定为并联头各关节位置的优化，即R、r、L的尺寸优化问题。由于R、r、L3个尺寸参数比例关系一定时，机构性质相同。利用初始传动角μ和长径比δ建立R、r、L尺寸参数的关系，初始传动角μ为并联头在3个H副驱动值相同时的分支传动角，长径比δ为连杆长度与驱动所在圆半径的比值，即

由于全局优化算法收敛速度较慢，局部优化算法对初值选择的敏感性较高，只能收敛到局部极值。为了提高运算速度并获得全局最优结果，采用试验加插值的方法进行混联机器人尺寸优化。通过试验对优化尺寸参数进行抽样，对目标优化函数结果进行插值，得到全尺寸区间的多目标综合优化函数值，流程如图7所示。

(1)给定尺寸优化范围及各优化指标权重系数

根据实际应用中整体尺寸轻巧性的需求，给定优化尺寸参数范围为μ∈[10°,80°]，δ∈[0.1,0.8]。优先考虑机器人并联头摆动范围和速度性能指标，给定τ1=0.5，τ2=0.05，τ3=0.4，τ4=0.05。

(2)确定试验方法

采用拉丁超立方抽样(Latin hypercube sampling，LHS)对机器人优化尺寸参数进行试验设计：在n维空间中，将每一维坐标区间等分为m个区间，保证每个因子的每个水平只研究一次，完成n维空间m个样本数的拉丁超立方抽样。此方法可以有效地对空间进行填充，减少研究点数。为了避免样本点的随机和不均衡性，对拉丁超立方抽样方法进行优化(记为OptLHS)，使所有点尽量均匀地分布在设计空间中，即实现两点距离最小值的最大化[26]。

本文将分别采用LHS和OptLHS对尺寸参数进行试验。此外，建立优化尺寸参数μ和δ的全因子尺寸参数矩阵，以便对抽样优化方法的准确性进行验证。

(3)试验结果及比较

设定m=29，分别采用LHS和OptLHS试验设计方法对优化尺寸参数进行抽样，建立2×29的尺寸参数。对优化尺寸参数μ和δ按照15×15进行均匀离散，建立全因子的尺寸参数矩阵，图8为LHS、OptLHS与全因子尺寸参数对比。

(4)对多目标加权综合优化函数进行计算

对包含各评价指标的混联机器人多目标综合优化函数进行计算，得到各抽样尺寸的加权综合优化函数值。

(5)对优化目标结果进行插值

采用三次插值法对LHS和OptLHS加权综合优化目标值F(x)进行插值，得到与全因子尺寸参数一致的15×15的综合优化指标F(x)矩阵。

(6)结果及准确性验证

在同样配置的环境中进行计算，全因子、LHS和OptLHS的最优参数值、目标函数值和所有时间结果对比如表1所示。

由表1可以看出，采用LHS加插值运算的优化方法的最优参数值与全因子计算的结果不一致，其误差由其采样随机性引起。采用均匀布置采样点的OptLHS加插值运算的优化方法保证了整体优化数据空间的完整性，比LHS加插值运算的优化方法更可靠，保证了优化准确率。采用OptLHS采样与插值运算结合的优化方法，所用时间仅为全因子优化的8%，极大地提高了优化效率。

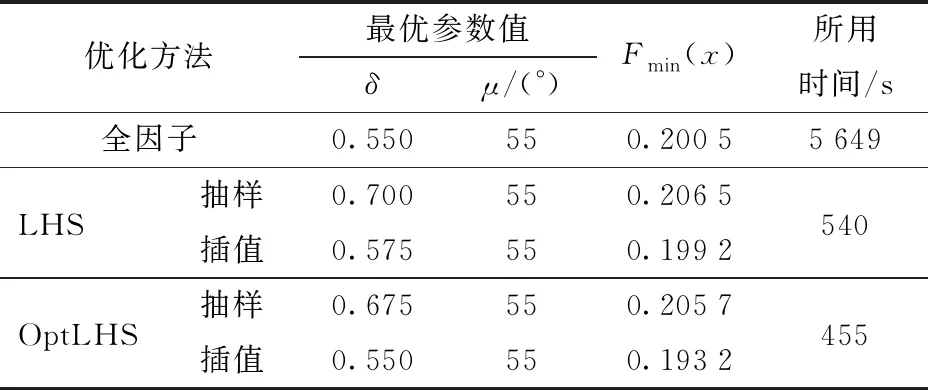
表1 全因子、LHS和OptLHS结果对比

3.4 性能图谱

通过3.3节计算，得到全尺寸设计空间的混联机器人转动能力θm、力传递性能Γ、速度性能κ和刚度性能σ指标的性能图谱，如图9所示。

4 优选尺寸及性能

根据具体应用条件，混联机器人X、Y导轨行程为800 mm，H副行程为600 mm，驱动分支H副所在圆半径R=86 mm。根据表1所示优化结果，设计参数取长径比δ=0.5，初始传动角μ=50°，圆整尺寸后可得并联头R2副所在圆半径r=113 mm，分支连杆长度L=43 mm。

对该优选尺寸下混联机器人的性能进行研究，其转角关系如图10所示。

可见，该尺寸下3-RHUR/PUS+PP五自由度混联机器人可实现全方位35°的摆动，在φ=60°、180°、300°附近时，可以达到55°摆动。

给定混联机器人X、Y导轨和并联头驱动同步输入的单位输入速度球体，得到混联机器人末端移动速度球体如图11所示。由图11可知，该五自由度混联机器人沿X、Y、Z方向移动输出速度满足各向同性，各方向速度传递性能相同。

给定并联头H副驱动单位输入速度球体，得到并联头末端转动和移动速度椭球体如图12所示。由图12可以看出，并联头沿X、Y方向转动速度和移动速度输出相同，且无Z方向转动速度输出。

混联机器人在初始位置和并联头摆角30°时的方向刚度如图13所示。由图13可以看出，混联机器人方向刚度与并联头末端方位有关，并沿方位轴线垂面对称。

5 结论

(1)提出一种带随动滑筒的并联头串联双导轨的混联五自由度机器人构型3-RHUR/PUS+PP，通过优化确定了混联机器人尺寸，并对其性能进行了分析。

(2)基于螺旋理论建立了串并混联的正逆运动学映射关系，为混联机器人整体性能研究奠定了基础。

(3)综合考虑混联机器人的转动能力、力传递性能、速度性能和刚度性能，建立了多目标加权综合优化函数，提出OptLHS采样与三次插值相结合的优化算法，以此对混联机器人进行多目标优化。该优化方法所需优化时间仅为同量级全因子优化的8%，证明了优化方法的有效性。