深刻认识“功能关系”
■张志强 李海燕
一、理解“功能关系”
1.重力做的功等于重力势能的变化量。重力做正功,重力势能减少;重力做负功(物体克服重力做功),重力势能增加。(重力势能的变化量与零势能参考平面的选取无关)
2.弹力做的功等于弹性势能的变化量。弹力做正功,弹性势能减少;弹力做负功,弹性势能增加。
3.合外力对物体做的功(各个外力做功的代数和)等于物体动能的改变量。合外力做正功,动能增加;合外力做负功,动能减少。(动能定理)
4.在只有重力或弹力做功的物体系统内,系统的总机械能保持不变。(机械能守恒定律)
5.除重力和弹簧弹力外,其他力做的总功等于物体机械能的改变量。其他力做正功,机械能增加;其他力做负功,机械能减少。(机械能守恒定律的引申)
二、应用“功能关系”
1.应用功能关系求解多过程运动问题。
例1 如图1所示,abc是竖直面内的光滑固定轨道,水平轨道ab段的长度为2R,四分之一圆弧轨道bc段的半径为R,两段轨道相切于b点。一质量为m的小球,始终受到与重力大小相等的水平外力F的作用,从a点由静止开始向右运动,重力加速度为g。小球在从a点开始运动到其能够到达的最高点的过程中,机械能的增加量为( )。
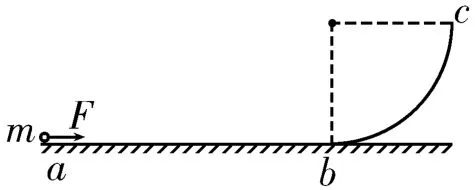
图1
A.2mgRB.4mgR
C.5mgRD.6mgR
点拨:小球能够到达的最高点不一定是c点,小球可能到不了c点,也有可能经过c点继续做斜上抛运动。

答案:C


图2

答案:AD
2.应用功能关系求解变力做功问题。

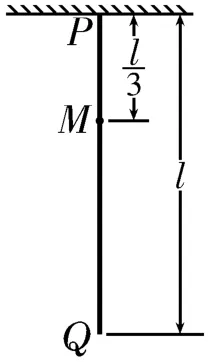
图3

点拨:用外力将细绳的下端Q缓慢地竖直向上拉起至M点的过程中,整段细绳只有下半段MQ运动,且做平动,除重力以外其他力做的功等于机械能的增加量。
我们先将矩形ABCD剪拼为边长分别为a″、b″的矩形A″B″C″D″,其中此处可参照文[1]中的方法;再对矩形A″B″C″D″执行(ⅰ)中的操作.

答案:A
变式:如图4所示,一根质量为m,长度为l的均匀链条一半放在光滑的水平桌面上,另一半悬在桌边,桌面足够高,桌角处约束链条的挡板光滑。将一个质量为m的小球分别拴在链条左端和右端,如图5甲、乙所示。在这三种情况下,将链条均由静止释放,当整根链条刚离开桌面时,关于它们的速度(设三种情况下三根链条的速度分别为va、vb、vc)大小关系,下列判断中正确的是( )。
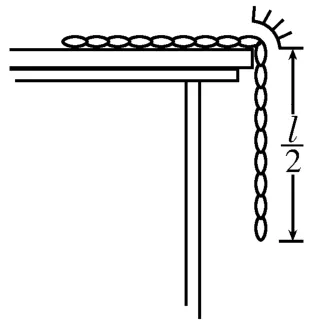
图4
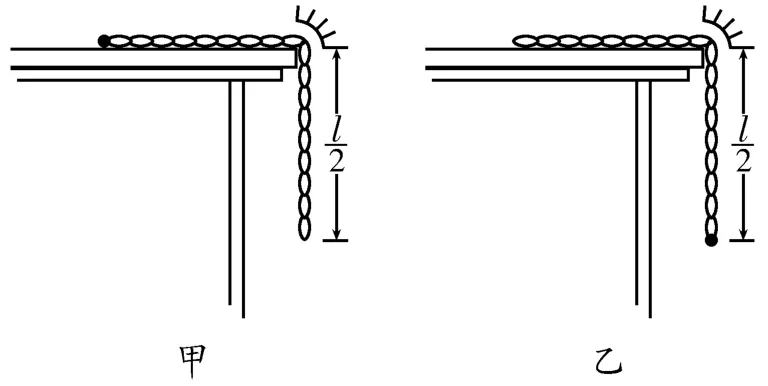
图5
A.va=vb=vc
B.va<vb<vc
C.vc>va>vb
D.va>vb>vc


答案:C


2.静止在水平地面上的一个小物体,在竖直向上的拉力作用下向上运动,运动过程中,物体的机械能与位移的关系图像如图6所示,其中0~h1过程的图像是曲线,h1~h2过程的图像为平行于横轴的直线,不计空气阻力。下列说法中正确的是( )。
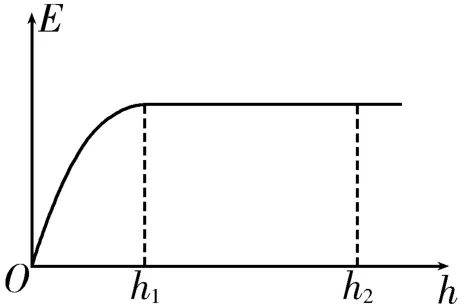
图6
A.0~h1过程中,物体所受的拉力是变力,且不断减小
B.h1~h2过程中,物体做匀速直线运动
C.0~h2过程中,物体的动能先增大后减小
D.0~h2过程中,物体的加速度先减小再反向增大,最后保持不变且等于重力加速度g
3.如图7所示,一条长度为L的均匀金属链条,一半在倾角为θ的光滑斜面上,另一半竖直向下垂在空中,斜面顶端约束链条的挡板光滑。当链条刚好全部滑出斜面的瞬间,它的速度为多大?
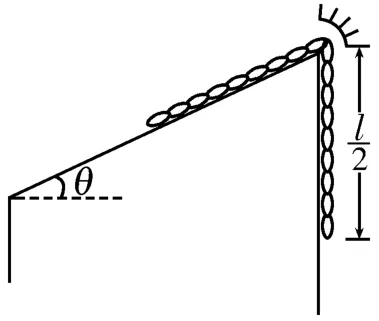
图7

图8
(1)传送带对物体做的功为多少?
(2)因摩擦产生的热量为多少?
(3)因传送物体,电动机多消耗的电能为多少?
参考答案:
1.A
2.ACD
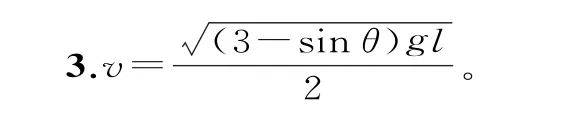
4.(1)W=255J;(2)Q=15J;(3)W多=270J。

