Deformation Argument under PSP Condition and Applications
Silvia Cingolaniand Kazunaga Tanaka
1 Dipartimento di Matematica, Universit`a degli Studi di Bari Aldo Moro, Via E.Orabona 4,70125 Bari,Italy
2 Department of Mathematics,School of Science and Engineering,Waseda University,3-4-1 Ohkubo,Shijuku-ku,Tokyo 169-8555,Japan
Abstract. In this paper we introduce a new deformation argument,in which C0-group action and a new type of Palais-Smale condition PSP play important roles. This type of deformation results are studied in[17,21]and has many different applications[10,11,17,21] et al. Typically it can be applied to nonlinear scalar field equations. We give a survey in an abstract functional setting. We also present another application to nonlinear elliptic problems in strip-like domains. Under conditions related to[5,6],we show the existence of infinitely many solutions. This extends the results in[8].
Key Words: Deformation theory,nonlinear elliptic equations,radially symmetric solutions,striplike domains,Pohozaev functional.
1 Introduction
We study nonlinear differential equations with scaling properties via variational methods. A typical example is the following nonlinear scalar field equations:

whereN ≥2 and we consider the existence of radially symmetric solutions. This type of problem appears in many models in mathematical physics and is well-studied by many authors. Especially Berestycki and Lions [5,6] and Berestycki, Gallou¨et and Kavian [7]obtained almost necessary and sufficient conditions for the existence of non-trivial solutions. More precisely they consider(1.1)under the following conditions
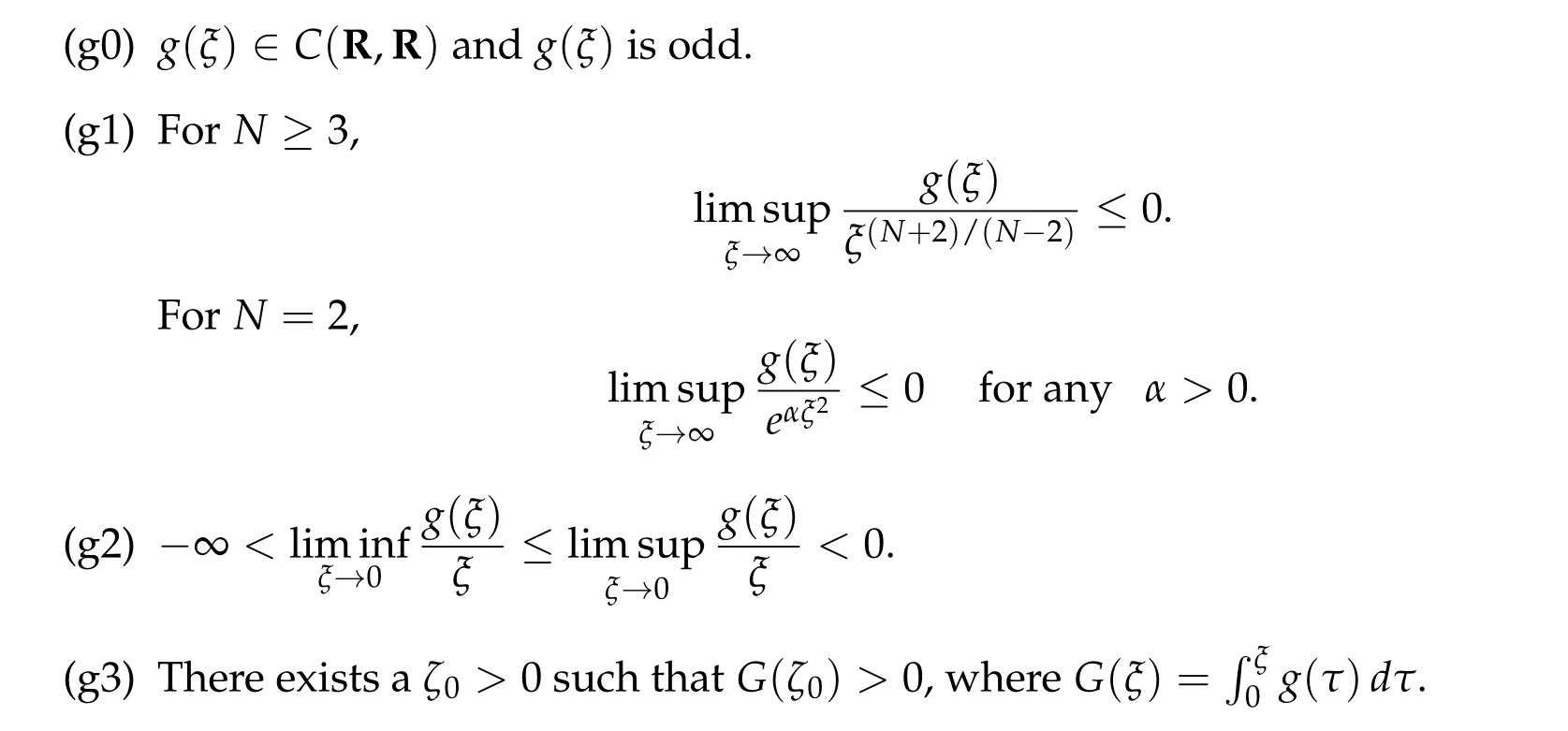
The[5,6](forN ≥3)and[7](forN=2)showed the existence of a positive solution of(1.1)and infinitely many possibly sign-changing radially symmetric solutions. We note that in[5–7]solutions are found as critical points of constraint functional

after a suitable scaling and solutions satisfy Pohozaev identity. See Coleman,Glazer and Martin [12] for related argument. We also note that a positive solution is obtained as a minimizer after scaling and it is a least energy solution.
Remark 1.1.WhenN= 2, in [7] the existence of solution is obtained under slightly stronger conditions(g0),(g1),(g3)and
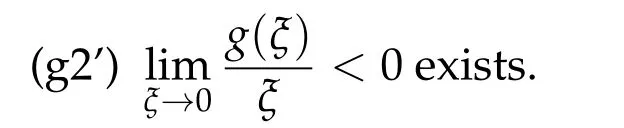
In[16], Hirata, Ikoma and the second author introduced a new approach to(1.1), in which we try to apply minimax argument to the natural functional associated to(1.1):
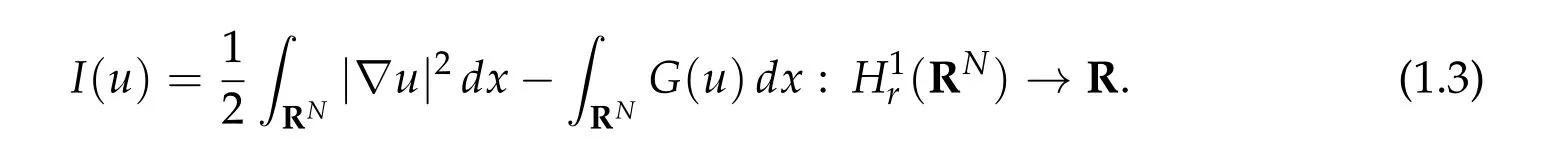
We note that it is difficult to verify so-called Palais-Smale condition ((PS) in short) forI(u) and we cannot apply the standard deformation argument directly toI(u). We also remark that the constraint functional(1.2a)and(1.2b)satisfy(PS)condition.
To avoid lack of (PS) condition, we make use of a special scaling property of the functionalI(u)and we introduce following Pohozaev functional:
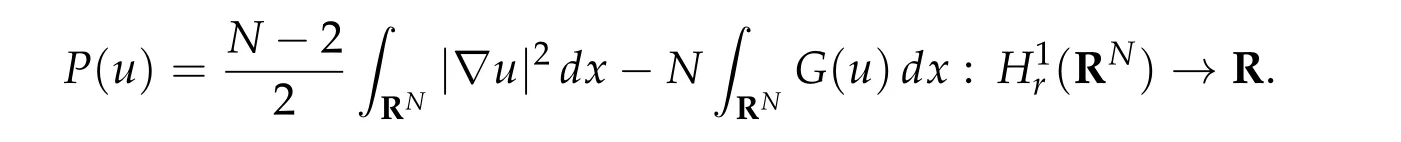
Using the scalinguλ(x)=u(x/λ),we have formally

In[16],Hirata,Ikoma and the second author found a(PS)sequence with an extra property at minimax levelb=infγ∈Γmaxξ∈D I(γ(ξ)).That is,there exists a sequence(uj)∞j=1⊂H1r(RN)such that asj →∞

For example,at a mountain pass level forI(u),they find a sequence(uj)∞j=1with(1.4a)–(1.4c) and under the condition (g0)–(g3) and moreover they show that (uj)∞j=1has a strongly convergent subsequence whose limit is a solution of (1.1). See Remark 4.1 in Section 4.
The condition (1.4c) means (uj)∞j=1satisfies Pohozaev identityP(u) = 0 asymptotically and we call such sequence(uj)∞j=1as(PSP)sequences.
Existence of such (PSP) sequences was firstly found by the second author. Jeanjean [22] used the second author’s approach forL2normalized solutions forL2super critical problems and in [16], we studied nonlinear scalar field equation (1.1) through(PSP) sequence and showed the existence of positive radially symmetric solutions via mountain pass method.
Such a strategy turned out to be useful for various problems with suitable scaling properties. See [23] for an application for nonlinear Choquard equations, [2,18–20] for fractional scalar field equations, [9] for FitzHugh-Nagumo elliptic systems, [8] for nonlinear elliptic equations in strip-like domains,[3]for nonlinear Schr¨odiger-Maxwell systems,[4]for nonlinear eigenvalue problems.
For even functionals, it is natural to ask the existence of infinitely many solutions.We note that our argument in [16] does not provide a deformation theory forI(u) and we cannot apply genus theory directly toI(u). So to find infinitely many solutions, we need to use some comparison argument to ensure the existence of unbounded sequence of minimax values. See[2,9,16].
In this paper we give a survey of some deformation theorems contained in previous papers [10,11,17,21] and a new application to semilinear elliptic equations in strip-like domains. Our deformation result works forI(u)under(g0)–(g3)and enables us to apply genus theory directly toI(u). It also shows that critical points with Pohozaev identity are essential in the deformation argument(see Corollary 3.1 and Remark 3.1 in Section 3). A special scaling property and a new type of Palais-Smale condition,which we call(PSP)condition and which claims any(PSP)sequence has a strongly convergent subsequence,play important roles in our argument.We give our deformation result in a general setting in Sections 2–3. We also give an existence result for(PSP)sequence at a minimax level in Section 4.
We note that such a deformation argument is firstly given in [17] forL2normalized problem for nonlinear scalar field equations. We also refer to [21] forL2super critical problems and [10,11] for our recent works onL2normalized solutions for nonlinear Choquard equations and fractional nonlinear scalar field equations.
In Section 5,we give a new application to a nonlinear elliptic problem in a strip-like domain:
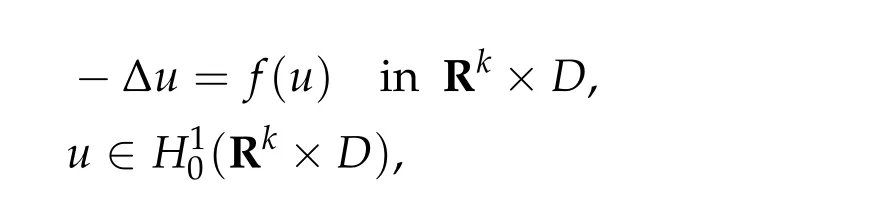
wherek ≥2. Under conditions(f0)–(f3)in Section 5, which are related to (g0)–(g3), we show the existence of infinitely many solutions.
2 Deformation argument under(PSP)
We give our deformation argument in an abstract framework. Let(E,)be a Hilbert space and Φ :R→L(E);θ ■→Φθbe a continuous group action ofR. ForI ∈C1(E,R)we assume
Assumption 2.1.
(i)Φθ is a C0-group action,that is,

(ii) Let M=R×E and we regard M as a Hilbert manifold and we introduce a metric by
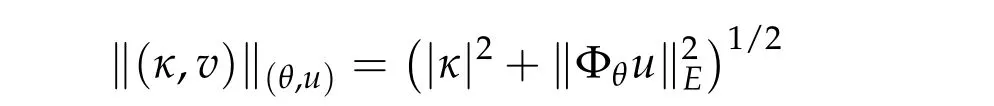
for all(κ,v)∈R×E=T(θ,u)M and(θ,u)∈M. We assume‖·‖(θ,u)is a metric of class C2.
(iii) Let

Then we assume that J(θ,u)∈C1(M,R).
Under the Assumption 2.1,we introduce
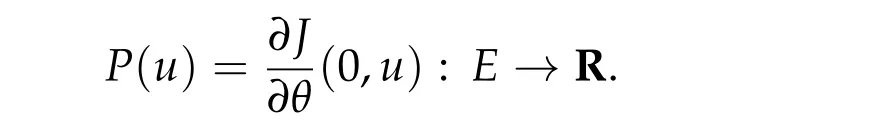
Forb ∈Rwe request the following Palais-Smale type condition(PSP)bforI(u).(PSP)bAssume that(uj)∞j=1⊂Esatisfies

Then(uj)∞j=1has a strongly convergent subsequence.
Under the above assumptions,we have the following deformation result in which we use notation:

We note thatKbis different from the usual critical set at levelband it requestsP(u)=0.
Theorem 2.1.Assumption2.1and for b ∈R(PSP)b holds. Then
(i)Kb is compact in E.
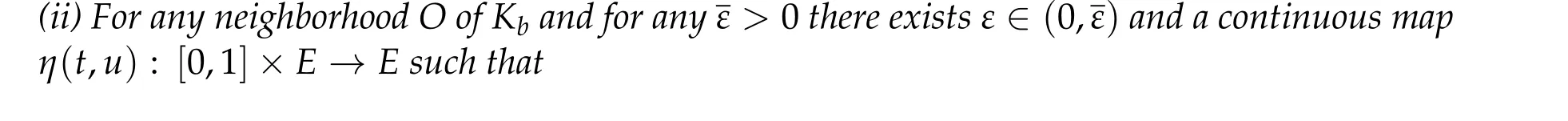
(1) η(0,u)=u for all u ∈E.
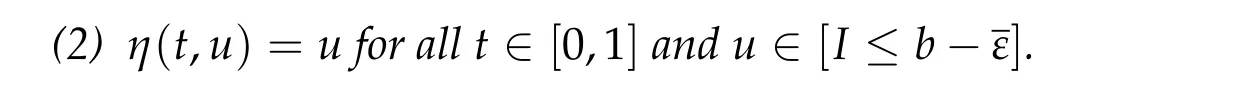
(3) I(η(t,u))≤I(u)for all(t,u)∈R×E.
(4) η(1,[I ≤b+ε]O)⊂[I ≤b −ε],η(1,[I ≤b+ε])⊂[I ≤b −ε]∪O.
(5) If Kb= ∅,then η(1,[I ≤b+ε])⊂[I ≤b −ε].
(6) If I(u)is an even functional,then η(t,−u)=−η(t,u)for all(t,u)∈R×E.
A typical situation, where the Assumption 2.1 is satisfied, is given in the following example.
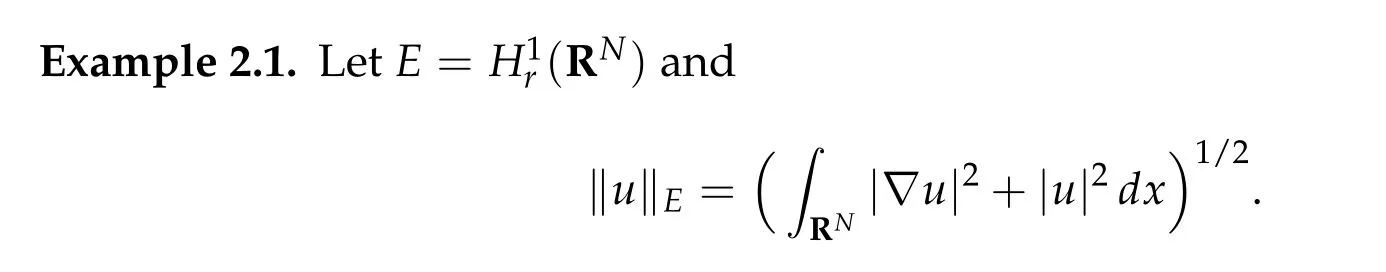
We consider the following action Φ :R→L(H1r(RN))defined by
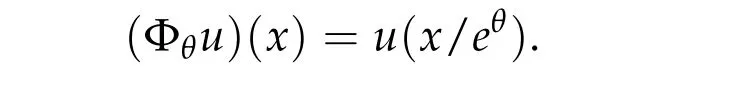
Then we have

ForI(u)∈C1(E,R)given in(1.3),we have

We note thatΦθuis not of classC1in general butJ(θ,u)is of classC1. That is,E,Φθsatisfy the Assumption 2.1. We also note that

We also note that under(g0)–(g3),I(u)satisfies(PSP)bcondition for allb ∈R(see Proposition 6.1 in[17])and we can find infinitely many solutions via symmetric mountain pass theorem.
The statement (i) of Theorem 2.1 is a direct consequence from (PSP)b. In Section 3,we give an outline of the proof of the statement(ii).
Remark 2.1.Theorem 2.1 can be generalized to the setting, where a functionalI(u) is defined on a submanifold inE. See[21], where applications toL2normalized solutions are also given.
3 Outline of the proof of Theorem 2.1
Proof of Theorem 2.1 is given using a deformation flow forJ(θ,u) :M →R. We begin with some notation. First we define the standard distance distMonMby
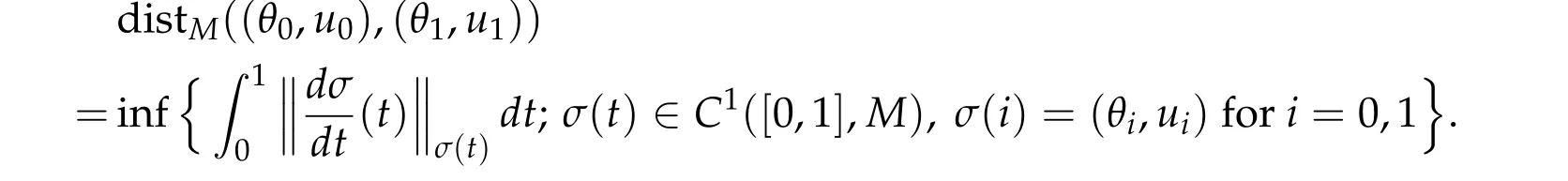
We have easily that
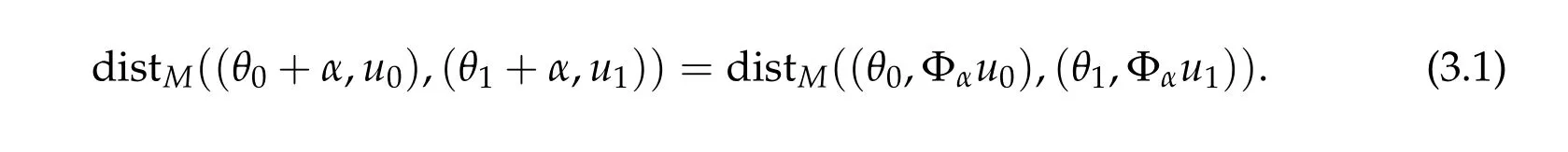
ForF ∈T∗(θ,u)M,we define its norm by
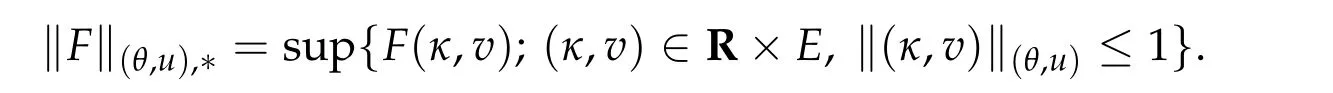
WritingD=(∂θ,∂u),we have
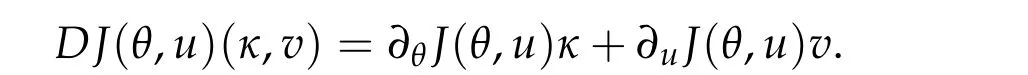
By the definition ofJ(θ,u),we have for(θ,u)∈M

In particular,

Finally forb ∈R,we set
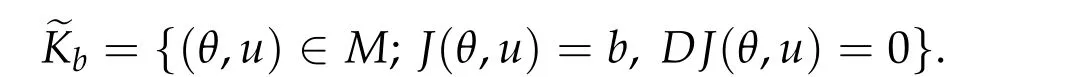
We note that

From the above properties we have
Lemma 3.1.Suppose Assumption2.1holds and for b ∈Rassume(PSP)b. Then(i)Let(θj,uj)⊂M satisfies
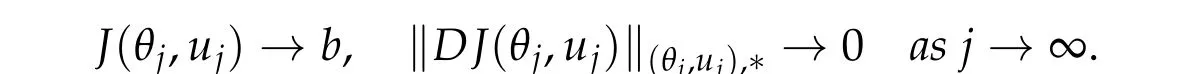
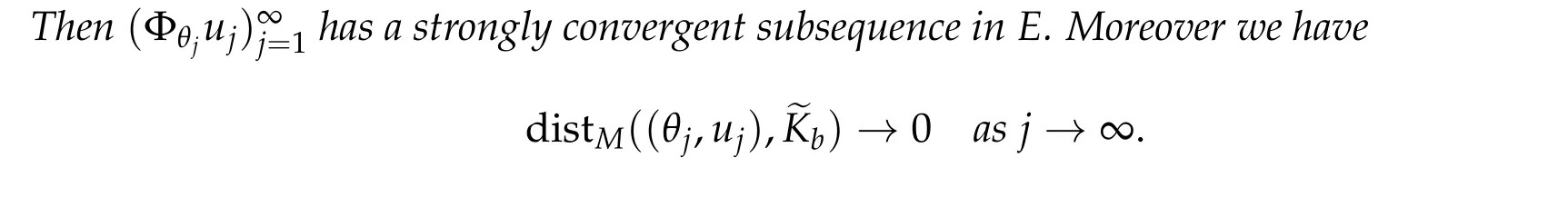
(ii)Suppose Kb/= ∅,i.e.,~Kb/= ∅. Then for any ρ>0there exists δρ>0such that
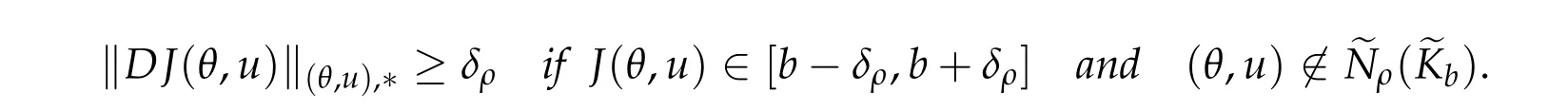
Here
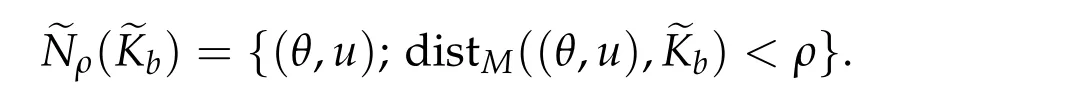
(iii)If Kb= ∅,i.e.,~Kb= ∅,there exists δ0>0such that

Proof.By(3.3)and(PSP)b,(i)follows. (ii)and(iii)follow from(i)easily.
We use notation
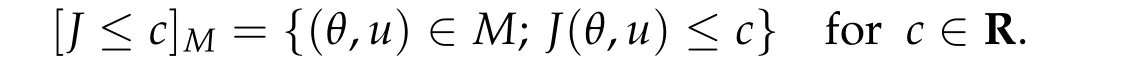

we consider the following ODE inM:

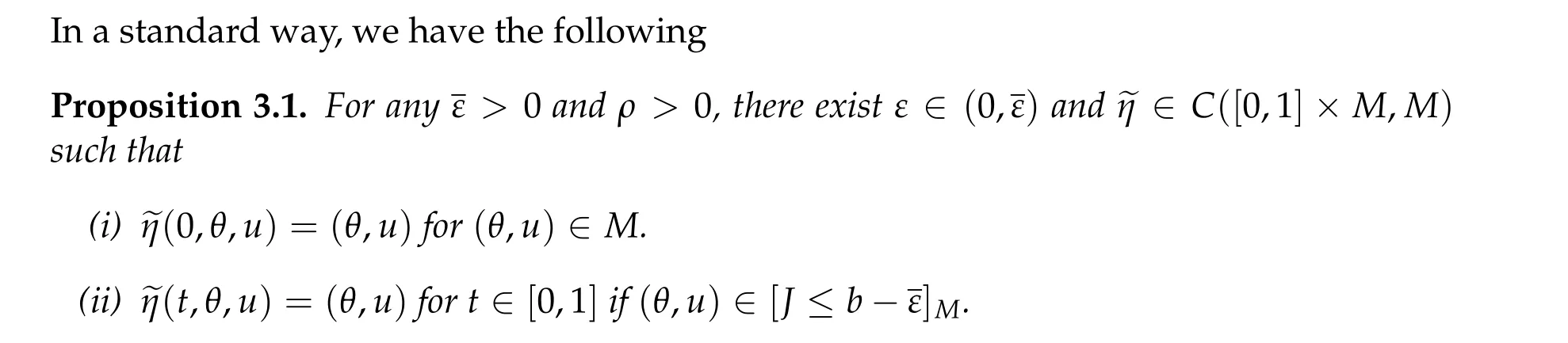
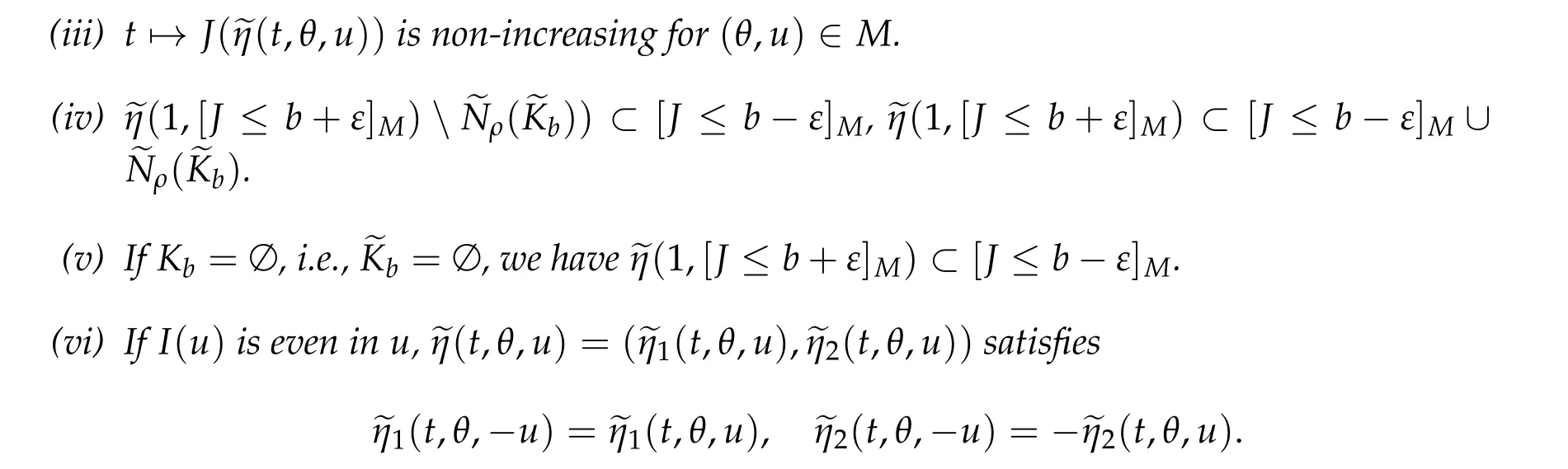
Our Theorem 2.1 can be derived from Proposition 3.1. We need the following operator:
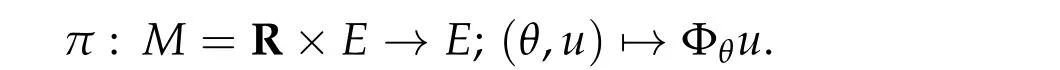
We need the following lemma.
Lemma 3.2.For any ρ>0there exists a R(ρ)>0such that

Here

Proof.Suppose that(θ,u)∈~Nρ(~Kb). By(3.1),note that

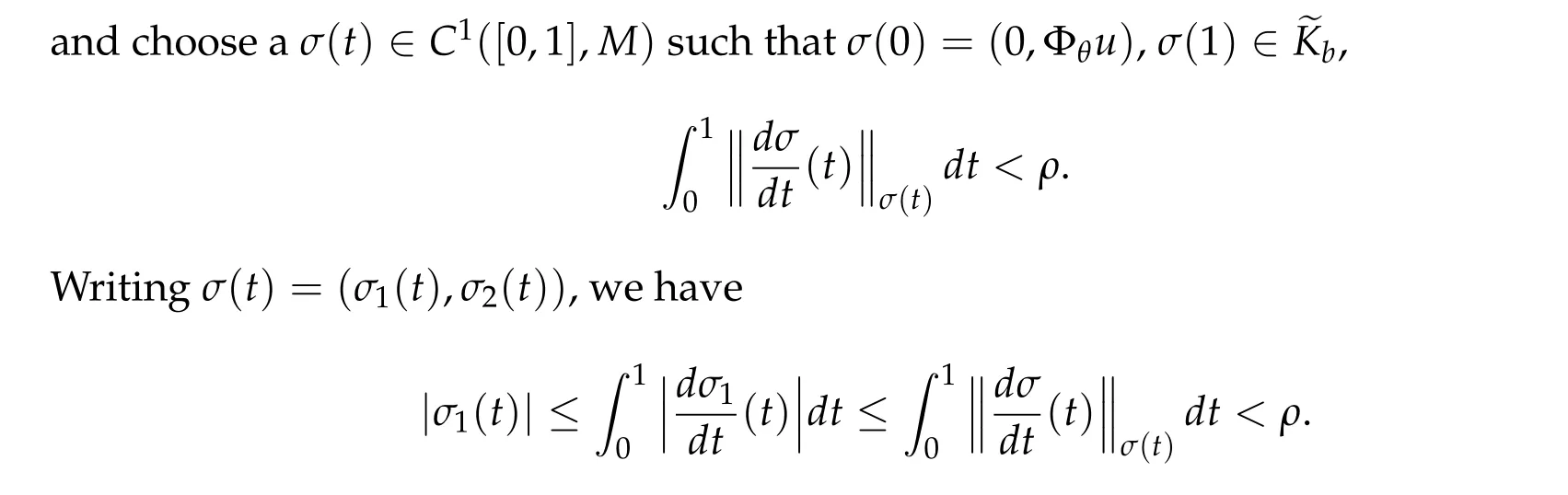
We note that there existscρ>0 such that for someδ ∈(0,1]
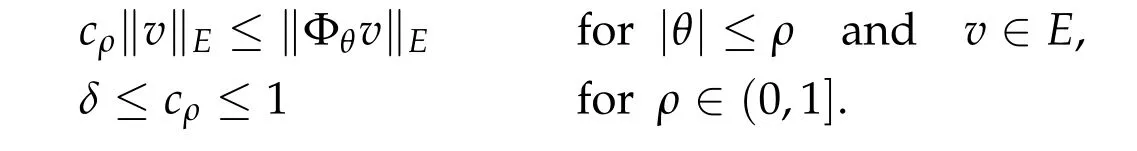
Thus
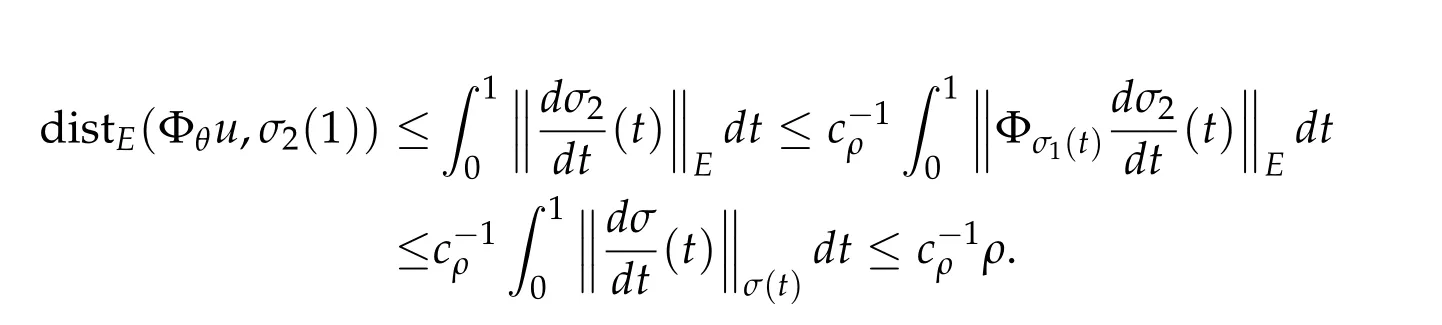
Therefore,noting Φσ1(1)σ2(1)∈Kb,
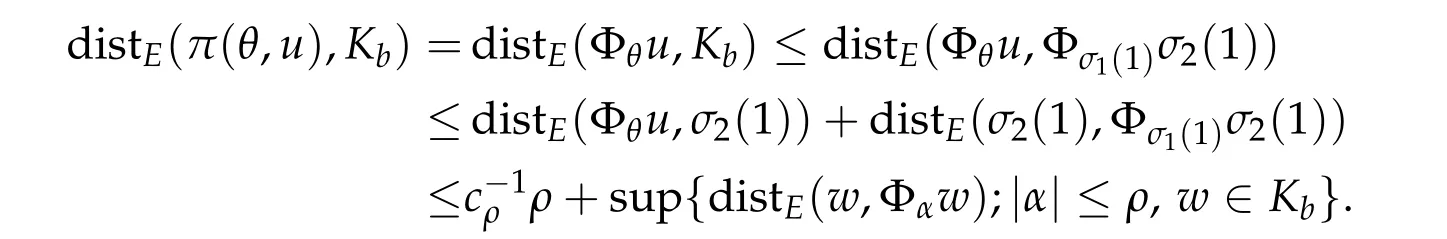
SinceKbis compact by(PSP)b,we have
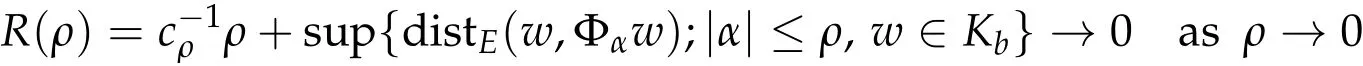
and(3.5a)and(3.5b)hold.
Proof of Theorem2.1(ii).For a given neighborhoodOofKb,we chooseρ>0 so small thatNR(ρ)(Kb)⊂O. By Lemma 3.2,we have
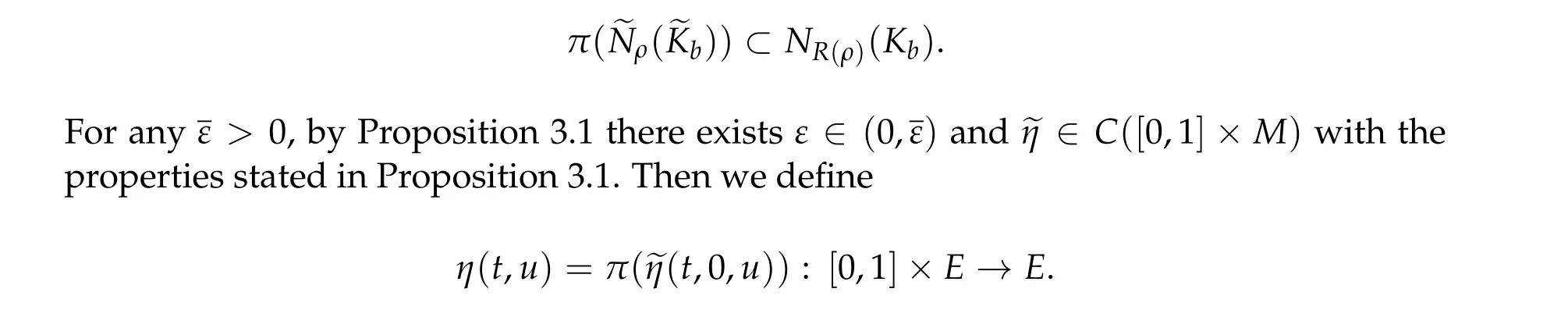
Then we can see thatηhas the desired properties.
As a corollary to Theorem 2.1,we have
Corollary 3.1.Suppose that Assumption2.1and(PSP)b hold. Moreover suppose Kb= ∅.Then there exists ε>0such that[I ≤b+ε]is deformable into[I ≤b −ε].
Remark 3.1.From Corollary 3.1, if (PSP)bholds forb ∈RandKb= ∅, then even if the standard critical set ^Kb={u ∈E;I(u) =b,I′(u) = 0}is not empty, [I ≤b+ε] is deformable into[I ≤b −ε]. Thus,critical points without Pohozaev identityP(u)=0 do not affect topology of level sets ofI.
4 Generation of(PSP)sequences at minimax level
Under the Assumption 2.1 (but without assuming (PSP) condition), we have the following existence result for (PSP) sequence at minimax levels. It can be regarded as a refinement of Ekeland’s principle under Assumption 2.1.
For the sake of simplicity,we state the result for Mountain Pass Theorem due to Ambrosetti and Rabinowitz[1].
Theorem 4.1.Suppose that Assumption2.1holds and I(u)has a mountain pass geometry. That is,for e ∈E with e/=0,set
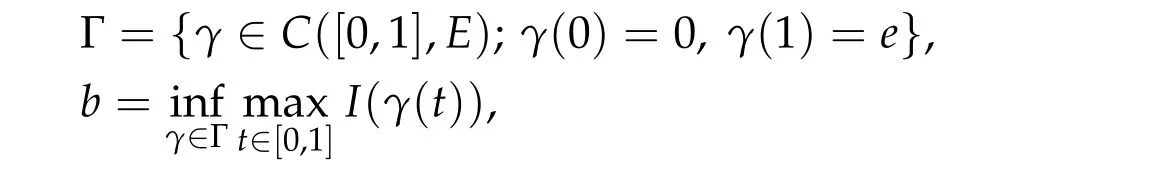
and assume

Thusη(t,u) =π(~η(t,0,u)) satisfies (1)–(3)and (5) in Theorem 2.1(ii). Now take a pathγ ∈Γ with maxt∈[0,1]I(γ(t)) This sequence is obtained by applying Ekeland’s principle toJ(θ,u)in[16]. Clearly in this setting,(Φθjuj)is a(PSP)bsequence forI(u). See also[23]for generation of(PSP)sequences. Our abstract results can be applied to many problems. For example, nonlinear scalar fields equations,nonlinear Choquard equations,etc. Here we give an application to a nonlinear elliptic problems in a strip-like domain: wherek ≥2 andD ⊂Rℓ(ℓ ≥1)is a bounded open domain with a smooth boundary∂D. formally we have We setN=k+ℓ ≥3 and we assume (f0)f(ξ)∈C(R,R)andf(ξ)is odd. To find critical points ofI(u),we restrictI(u)to a space of axially symmetric functions inx: Our main result in this section is Theorem 5.1.Assume(f0)–(f3). Then I(u) :H1s,0(Rk×D)→Rhas a unbounded sequence of critical values. In particular,(5.1)has infinitely many solutions which are axially symmetric in x,that is u(x,y)=u(|x|,y). Remark 5.1.Introducing a suitable truncation off(ξ), the condition(f1)can be relaxed to(see[8,Section 2]) Remark 5.2.(i) Under condition(f0),(f1’),(f2),(f3)but without oddness off(ξ),existence of a least energy solution is shown in[8]. (ii) We refer to Esteban[13]and Grossinho[15]for earlier works. In[13,15],they study the case whereG(s)/s−θis non-decreasing in[0,∞)for someθ>2. Remark 5.3.In view of (5.2), conditions (f0)–(f3) are analogies of (g0)–(g3) for elliptic problems in strip-like domains(5.1). It seems difficult to take an approach in spirit of[5,6]: find critical points of Then andE,Φθsatisfy the Assumption 2.1. We also defineP(u) :E →Rby setting We have the following Proposition 5.1.Assume(f0)–(f3). Then for any b ∈R, I(u)satisfies(PSP)b. This proposition is essentially shown in [8, Sections 5–6]. In fact, in [8], it is shown that if(θj,uj)∈R×Esatisfies then(θj,uj)has a convergent subsequences. Consider a special caseθj ≡0. It is nothing but(PSP)bcondition. By Proposition 5.1 we can apply Theorem 2.1 toI(u)and we have deformation flow forI(u). We apply Symmetric Mountain Pass Theorem toI(u). First we note that by(f2)and(f1) Sincem0<λ1(D),we have for somer0,ρ0>0 To find symmetric mountain pass geometry,we need the following result due to[6]. To state it,we need some notation. Forn ≥1,we set Berestycki and Lions[6]showed the following Proposition 5.2.For R> 0there exists a continuous map τn,R:πn−1→Lip([0,∞),R)such that (1)suppτn,R(ξ)⊂[0,R]for all ξ ∈πn−1. (2)τn,R(ξ)(r)∈[−1,1]for all ξ ∈πn−1and r ∈[0,∞). (3)τn,R(−ξ)(r)=−τn,R(ξ)(r)for all ξ ∈πn−1and r ∈[0,∞). (4)For each ξ ∈πn−1,τn,R(ξ)(r)∈{+1,−1}on[0,R]except in at most n intervals J1,···, Jp of[0,R],each of these intervals has length at most one. Moreover This proposition is shown in Sections 9.2a,9.2b in[6](setζ=1 in the argument in[6]).We note thatτn,R(ξ)is explicitly given in[6]. Regarding we have We also see that Forξ ∈Rk,we write and we defineγ0n:Rn →Eby Hereζ0(y)is given in(f3). We also note that by(5.4) Lemma 5.1.For each n ∈Nthere exists Rn>0such that Proof.Letu(x,y) =γ0n(ξ)(x,y) for|ξ|1=R. We have by the definition ofτn,R(ξ) and Proposition 5.2(1)–(4) Here we use notation:BR={x ∈Rk;|x|≤R}. Since so Thus,settingC1=2 ∫ D|ζ0(y)|2dy, On the other hand,settingC2=maxt∈[0,1]|G(tζ0(y))|,we have Thus we have Since G(ζ0)> 0, we haveI(u)< 0 for largeR. Thus for largeRn> 0 we have the conclusion of Lemma 5.1. Proof of Theorem5.1.By Lemma 5.1,we chooseR1,R2,···,so that such that We may also assume wherer0>0 is given in(5.3). Now we define a sequence of minimax values. We set forn ∈N and we define We note that by(5.7) Thus,bn ≥ρ0for eachn ∈Nand we can see thatbnis a critical value ofI(u) for eachn ∈N.To show the multiplicity of critical points,we need another set of minimax values.Modifying the definition in[24],we set Here genus(Y)is the genus ofY. Clearly we have By our deformation result (Theorem 5.1), we can apply the argument in [24] tocn. In particular,sinceI(u)satisfies(PSP)bfor anyb ∈R,we have ThusI(u)has unbounded sequence of critical values. Acknowledgments The first author is supported by PRIN 2017JPCAPN”Qualitative and quantitative aspects of nonlinear PDEs”and by INdAM-GNAMPA.The second author is supported in part by Grant-in-Aid for Scientific Research(JP19H00644,JP18KK0073,JP17H02855,JP16K13771 and JP26247014)of Japan Society for the Promotion of Science.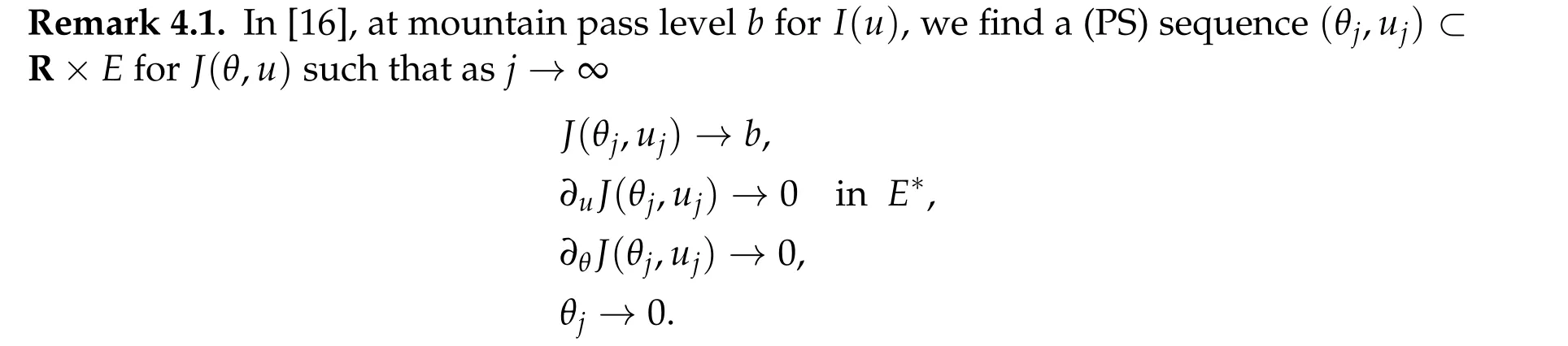
5 An application to nonlinear elliptic problems in strip-like domains

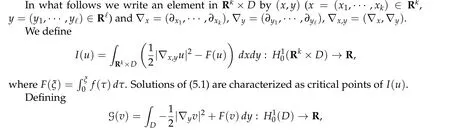
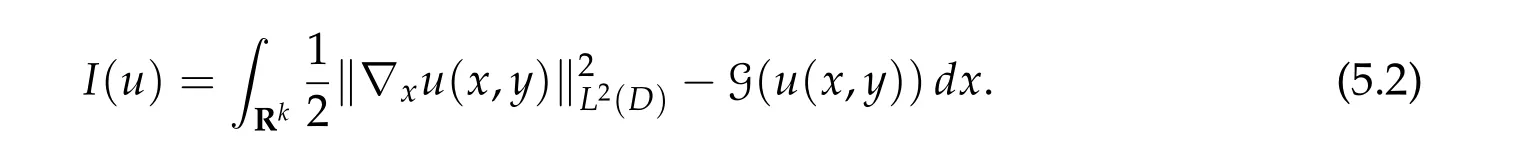



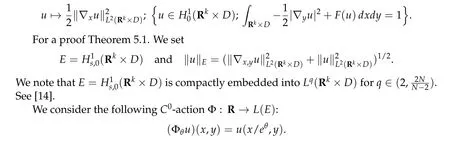


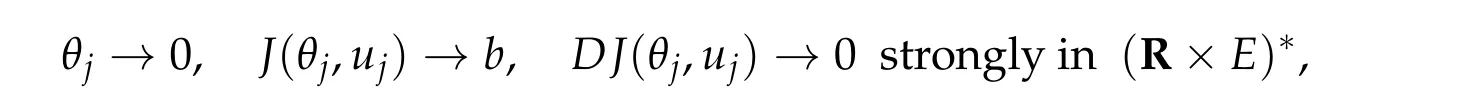
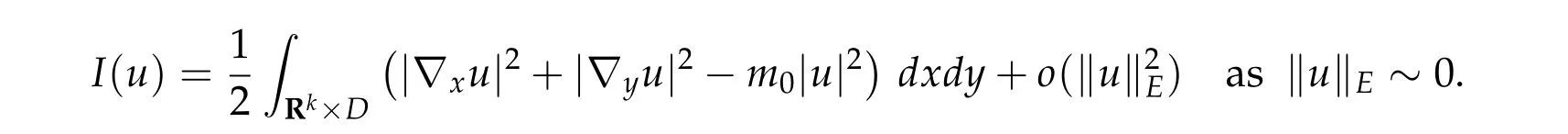
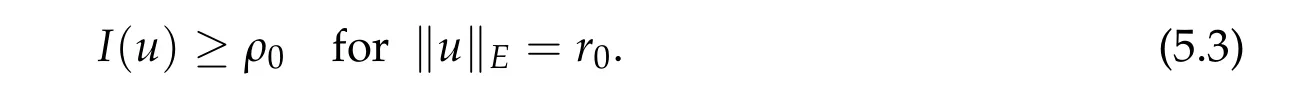
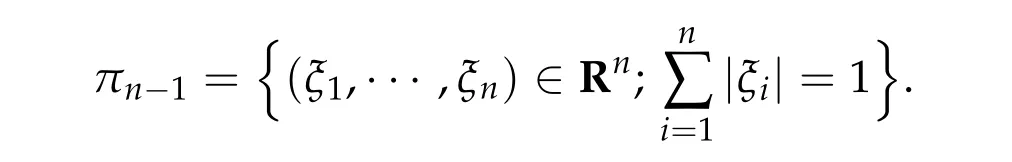

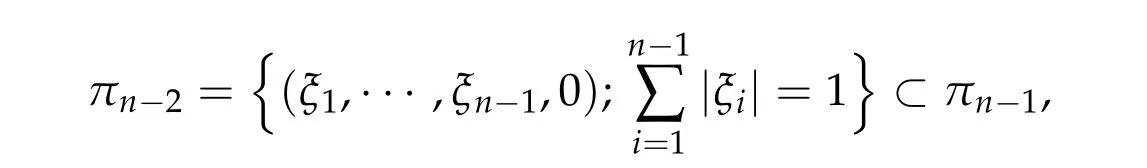




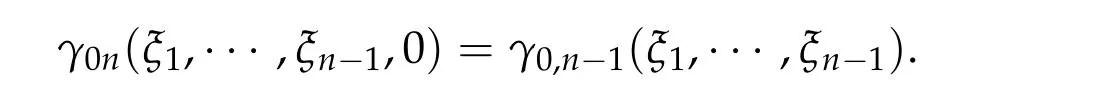
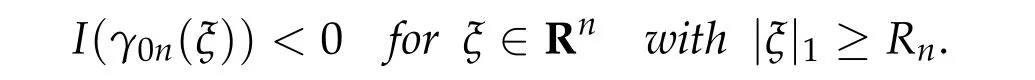

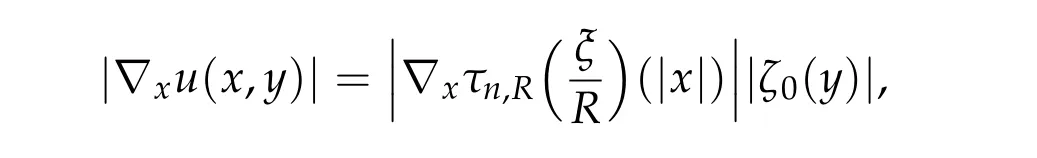
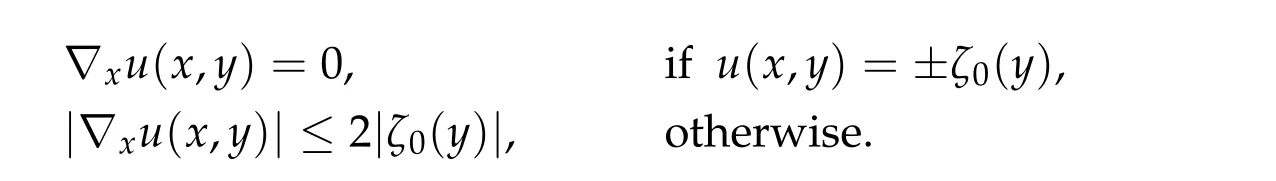
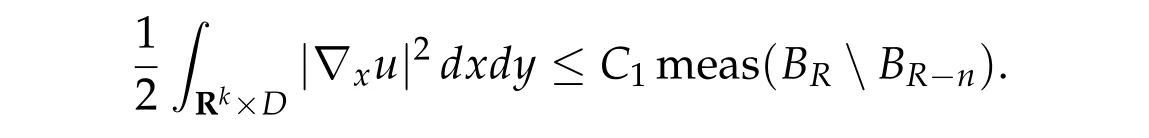
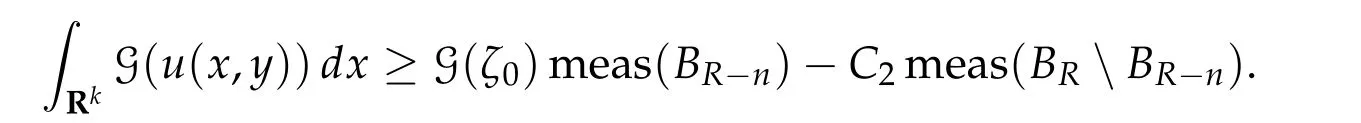

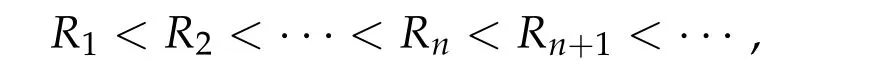








 Analysis in Theory and Applications2021年2期
Analysis in Theory and Applications2021年2期
- Analysis in Theory and Applications的其它文章
- Classification of Positive Ground State Solutions with Different Morse Indices for Nonlinear N-Coupled Schr¨odinger System
- Ground States to the Generalized Nonlinear Schrdinger Equations with Bernstein Symbols
- Index Iteration Theory for Brake Orbit Type Solutions and Applications
- Diffusion with a Discontinuous Potential: a Non-Linear Semigroup Approach
- Multiple Sign-Changing Solutions for Quasilinear Equations of Bounded Quasilinearity
- Ground States to the Generalized Nonlinear Schr¨odinger Equations with Bernstein Symbols
