基于Prophet算法的快销服装销售预测∗

苏 新

（江苏科技大学 镇江 212000）

1 引言

生成产品级销售预测是服装电商平台成功运营的关键因素。准确可靠的产品销售预测，可以及时把握客户需求的新动向，从而推出适销对路的产品和高质量的服务。实现优质的库存计划，可以减少对饱和市场过量不必要的冗余生产，降低成本。准确的调包计划任务，有效降低供需不匹配情况出现的概率，提高有效销售转化率，从而实现利润的最大化。

相较于传统行业，电商平台的商业环境是高度动态且不稳定的，这主要是由假日效应，竞争者行为等因素引起［1］。而与一般产品相比，快销服装的销售情况除了受商品自身品质，市场供求关系等因素影响，还在很大程度上跟节假日效应，产品宣传与推广促销活动等客观因素息息相关，而这部分变化往往是非线性和随机的，单纯使用线性模型很难预测出良好的结果。由于产品本身更迭速度很快，生命周期短，造成有效可用业务数据较少，且由于具有季节性、周期性、趋势性和主观性的特点，销售数据很大程度上也会受到地域、天气等因素的影响，从而呈现出较为复杂特殊的情况［5～6］。

本文提出一种基于Prophet的优化算法［4］，优化时间序列分解得到的各因式项模型，并综合考虑了真实销售中存在的诸多影响因素。解决了以往的模型在数据噪声大的情况下预测精度差的问题［2～3］，并且当数据量有限时，其预测结果也较为可靠。最终实验表明本文优化算法预测准确度要优于算法。

2 数据预处理

从数据库抽取原始业务数据，清洗数据集并对缺失数据，异常值和分类数据进行特征工程处理。

出于对业务数据的理解。销售时间上，将销售数据的日期换算成对应农历，数据向量增加节气特征。由于农历二十四节气对应地球公转位置，相较而言比公历的十二月份更能准确地反应不同阶段气温变化。销售空间上，由于具体到某家线下店铺的销售数据量过少，且不同店铺销售情况受地段、客流等复杂因素影响呈非规律性变化，因此精准预测具体店铺销售量显然不现实。中国地跨几十个纬度，温度梯度的水平变化明显，从南向北，气温随纬度增高而递减，随之带来的影响是不同区域产品的生命周期有着极大的差异。例如海南地区的夏季短袖产品的生命周期要比东三省长的多。考虑将所有店铺以省市划分，可以将空间上温度规律性变化体现在数据向量上。气温对于服装销售影响巨大，因此为提高预测准确率，考虑气温影响因素，将业务数据向量空间上以省市归类划分，时间上以农历阶段划分。

3 Prophet算法实现

服装销售预测是标准的复合型时间序列。一般来说，在实际生活和生产环节中，除了季节项、趋势项、剩余项之外，通常还有节假日的效应。将时间序列y(t)分解［7～10］，考虑以上四项，有：

其中g(t)表示趋势项，表示时间序列在非周期上面的变化趋势；s(t)表示周期项，或者称为季节项，一般来说是以周或者年为单位；h(t)表示节假日项，表示在当天是否存在节假日；εt表示误差项或者称为剩余项。通过拟合以上四项累加可以得到时间序列的预测值。

3.1 趋势项模型g(t)

选择基于逻辑回归的函数进行趋势项计算。逻辑回归的一般形式如：

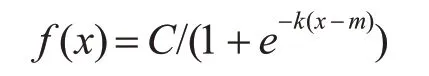
C称为曲线的最大渐进值，k表示曲线的增长率，m表示曲线的中点。当C=1，k=1，m=0时形成sigmoid函数形式［11］。它满足微分方程：y′=y(1-y)。

使用分离变量法来求解微分方程就可以得到：

但是在现实环境中，函数f(x)=C/(1+e-k(x-m))的三个参数C、k、m不可能都是常数，而很有可能是随着时间的迁移而变化的，因此考虑把这三个参数全部换成了随着时间而变化的函数，也就是C=C(t)，k=k(t)，m=m(t)。

3.2 季节性趋势s(t)

由于时间序列通常会随着天、周、月、年等季节性的变化而呈现季节性的变化，也称为周期性的变化。使用傅立叶级数来模拟时间序列的周期性。假设P表示时间序列的周期，P=365.25表示以年为周期，P=7表示以周为周期［12］。它的傅里叶级数形式为

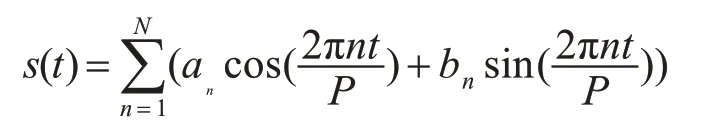
对于以年为周期的序列（P=365.25），N=10。对于以周为周期的序列（P=7），N=3。参数形成列向量：

当N=10时

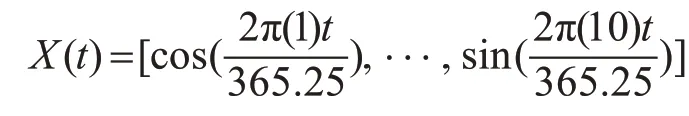
当N=3时

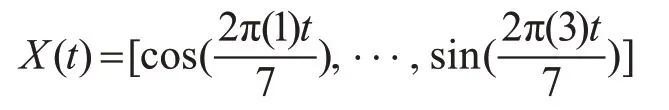
时间序列的季节项是s(t)=X(t)β，而β的初始化是 β～Normal(0，σ2)。σ值越大，表示季节效应越明显，值越小，表示季节效应越不明显。

3.3 节假日效应h(t)

在现实环境中，除了日常周末，节假日所产生的额外客流也会大幅度影响销量。由于每个节假日持续时间不同，例如春节、国庆节是七天的假期，而劳动节等假期时间较短。前后时间窗口值不同，对时间序列的影响程度不一样，因此不同的节假日可以看成相互独立的模型，并且可以为不同的节假日设置不同的前后窗口值，表示该节假日会影响前后一段时间的时间序列［13］。

对与第i个节假日来说，Di表示该节假日的前后一段时间，Ki表示节假日的影响范围。假设有L个节假日，那么其中

其中k～Normal(0，v2)，并且该正态分布是受到v这个指标影响的。参数v用来控制节假日的灵活度。默认值是10，当值越大时，表示节假日对模型的影响越大；当值越小时，表示节假日对模型的效果越小。

3.4 模型拟合

如上，时间序列已经可以通过趋势项、季节项、节假日项来构建完成：

使用了pyStan开源工具中的L-BFGS方法来进行函数的拟合，能够在较快的时间内得到需要预测的结果。

4 实验验证

数据库抽取原始业务数据经特征处理后，随机选择某时间段，将特征向量传入拟合模型中，将预测结果与实际值对比绘图。黑点表示原始的时间序列离散点，深蓝色的线表示使用时间序列来拟合所得到的取值，绿色橙色上下两条线表示时间序列的一个置信区间，表示合理预测的上下界。实验结果说明本文提出方法可以有效地应用于快销服装的销售预测。

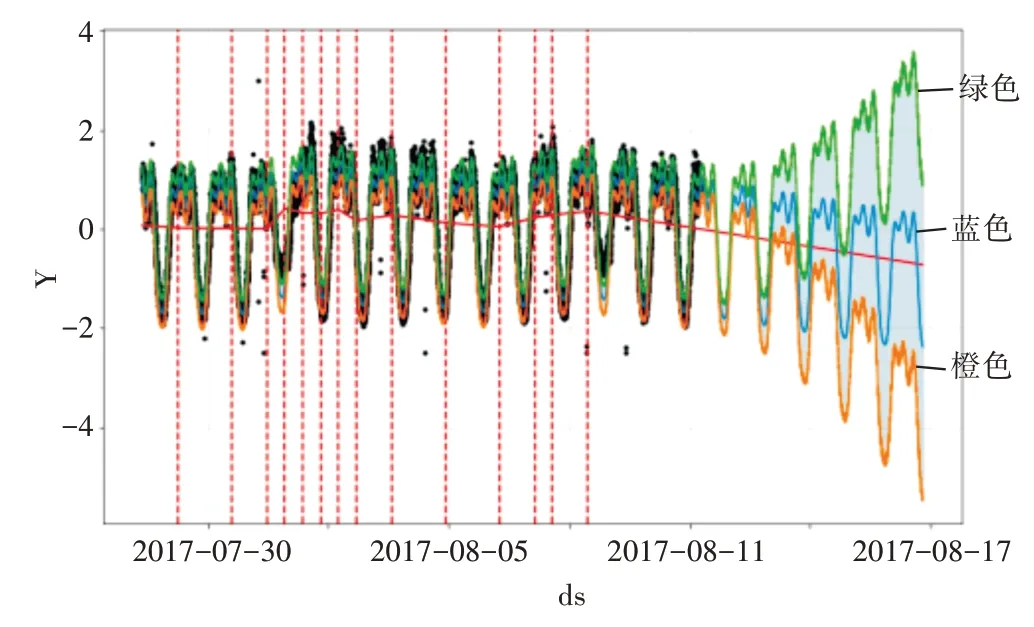
图1 基于模型预测的置信区间与真实值对照

5 结语

将优化后的Prophet算法模型同其他几种常见时序预测方法对比，并使用MAPE指标衡量模型优劣。根据实验结果，相比其他传统时序模型，优化后的Prophet表现优异，显著降低了预测误差。

其中naive是仅利用上一时刻序列值预测之后所有值的方法。snavie类似于naive方法，不过它考虑了季节性因素，周期性的以上一时刻数据预测下一周期相同位置时刻的数据。mean方法使用了数据平均值预测。arima是自回归综合移动平均方法。ets是指数平滑方法。

根据如上折线图对比观察，可以看出Prophet通过多项拟合，加入节假日数据做决策树准，并通过指定变点引导趋势项，使它在实验结果上表现优异，同其他常见的模型相比具有一定优势。但是它作为传统时间序列预测方法的延展，加不了除日期外的其他特征，考虑后期可利用机器学习模型取长补短，通过模型融合来进一步提高精确度。