计及预测误差影响的电力系统异质多能源经济调度研究∗

刘起兴 王 科 聂涌泉 徐克强 金朝意

（1.中国南方电网电力调度控制中心 广州 510663）（2.南京南瑞继保电气有限公司 南京 211102）

1 引言

在大力发展可再生能源相关政策的引导下，风力发电和太阳能发电因具有清洁无污染和成本低廉等优势，目前已成为可再生能源领域最具发展前景的能源形式［1］，风力发电和太阳能发电接入电网的规模越来越大，为能源战略带来了多方面的效益，但风能和太阳能具有很强的不确定性，电力系统的经济调度也受到了很多不利的影响［2］。为使得风力发电和太阳能发电等可再生能源得到更好的发展，同时提高电力系统的经济运行水平及安全稳定性，需对风力、太阳能的不确定性给电力系统带来的影响进行深入的研究。

针对风光等可再生能源对电力系统的影响，国内外学者进行相关的研究工作。文献［3］研究了风力发电不确定性给电力系统造成的影响，引入了风电出力不确定成本，将电力系统经济优化调度中的不确定性问题转换成了确定性的区间问题，从而有效地降低了电力系统经济调度模型的复杂程度。文献［4］对太阳能发电的不确定性问题进行了研究，在电力系统经济调度模型中考虑了太阳能发电预测误差的影响，优化模型中引入经济补偿成本。文献［5］将电力系统调度模型中的风力发电出力和太阳能发电出力分别等效为模糊随机变量和模糊变量，建立了双重不确定环境下的机会约束模糊随机经济调度优化模型。以上文献在对含风光经济调度的研究都未计及风光发电互补及由风光发电预测误差造成的补偿和惩罚成本。

本文建立了一种计及风能、太阳能出力预测误差影响的异质多能源电力系统经济调度优化模型，通过包含风能、太阳能和火力发电的经济调度仿真模型验证了本文方法的有效性。

2 风光预测误差分布分析

2.1 太阳能发电出力预测误差分布

太阳能发电中的光伏阵列一般均采用最大功率点跟踪控制的策略，太阳能发电出力的大小直接由光照强度决定［6］。因此，太阳能发电出力的预测值直接由光照强度的预测值决定，太阳能发电出力的预测误差和光照强度的预测误差两者之间紧密相关。假设光照强度预测误差服从均值为0且标准差为sk的正态分布，则根据光照强度和太阳能发电中光伏阵列输出功率函数关系可得

式中：ηs表示光伏阵列的转换效率，Is表示光照强度，单位为kW/m2，Ss表示太阳能光伏阵列的总面积大小，单位为m2。

根据式（1）中所示的线性关系，基于正态分布的性质可得不同时刻光伏出力预测误差仍然服从正态分布，表示为，其概率密度函数可表示为

2.2 风电出力预测误差分布

风电出力预测的研究主要包括直接预测和先预测风速再计算风电出力。风电出力预测误差受预测时间尺度、风电场规模大小和风速大小等多种因素的影响，预测结果仍然存在着很多不确定性，统计结果表明，风电出力预测误差水平在不同的风速段差别较大，风电出力预测误差尚无准确的分布形式来进行描述，虽然风速预测误差服从正态分布，但风电出力预测误差不服从该分布［7］。模糊随机变量具有模糊性和随机性，本文引入模糊随机变量风电出力预测误差来描述，则时刻t风电出力预测误差的表达式为

3 计及预测误差影响的经济调度模型

3.1 经济调度模型目标函数

计及风光预测误差的影响，电力系统经济调度的目标函数可表示为

式中：F1表示火力发电的经济成本，F2表示环境污染的经济成本，F3表示风力发电和太阳能发电的经济成本。

火力发电的经济成本F1可表示为［8］

式中：T=24h表示研究周期的时段数，N表示系统中火力发电的机组总台数，pit和 （fpi）t分别表示机组i在时刻t的发电功率和运行费用，Sit表示机组i在时刻t的开机成本，uit表示机组i在时刻t的开停机状态，开机状态、停机状态分别对应的值为1和0，ai、bi、ci分别表示机组i的耗量特性系数。

环境污染的经济成本F2可表示为［9］

式中：Cg、f（gpi）t分别表示环境污染的成本价格和机组i污染气体的排放量，αi、βi、γi、ζi、λi分别表示机组i的排污特性系数。

风力和太阳能发电的经济成本F3可表示为

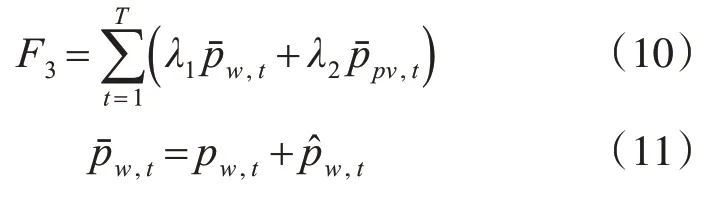
式中：λ1、λ2分别表示风力发电和太阳能发电的发电单价，分别表示时刻t风力发电和太阳能发电的输出功率实际值和预测功率值。

3.2 经济调度模型约束条件

在风力发电预测值和太阳能发电预测值给定的情况下，电力系统需满足的功率平衡约束条件可以表示为

式中：pL，t表示电力系统时刻t的负荷大小。

系统中各机组在时刻t的出力约束可表示为

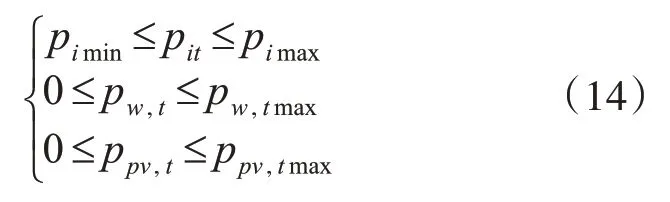
式中：pimin、pimax分别表示火力发电机组i在时刻t所允许的最小和最大出力，pw，tmax、ppv，tmax分别表示风力发电和太阳能发电在时刻t计划出力的最大值。

火力发电机组和风力发电机组在时刻t还需满足如下形式的爬坡约束［10］：

式中：rt，iu、rt，id分别表示火力发电机组i在时刻t的上、下爬坡速率，rt，wu、rt，wd分别表示风力发电机组在时刻t的上、下爬坡速率，T表示在时刻t内的任意一时间点，ΔT表示相邻时间点的时间间隔大小。

电力系统备用约束包括机组的正、负旋转备用约束和旋转备用总量约束［11］，可表示为

4 经济调度模型求解方法

电力系统经济调度优化模型是一个高维数、离散、非线性的大规模复杂工程优化问题，本文采用遗传算法与粒子群算法相结合的智能算法来对模型进行优化求解。遗传算法具有全局搜索能力强的优点，但其局部搜索能力较差［12］，而粒子群算法具有较强的局部搜索能力，但其全局搜索能力较差［13］，两种算法之间有很强互补性，将遗传和粒子群进行有效融合能取得更好的优化效果。两种算法的融合基本思路：利用粒子群算法对获得的初步解进行局部搜索寻优，以获得局部最优解，再将获得的局部最优解传递给遗传算法进行选择、交叉、变异操作以进行全局寻优。遗传算法中交叉概率和变异概率的值对算法的性能有重要影响，结合相关文献资料［14］，为改善算法的寻优搜索性能，本文按照算法中个体的性能表现来选取相应的交叉概率和变异概率，改进后的交叉概率和变异概率的表达式为

式中：fmax、favg分别表示种群中最大及平均适应度值，f′为交叉操作的两个个体中较大的适应度值，f为变异操作的个体的适应度值。

传统粒子群算法存在着初始粒子相似的情况，导致算法收敛速度较慢，为保证初始化粒子群的随机性和多样性，结合相关文献资料［15］，本文将混沌序列思想应用于粒子群算法，粒子群位置和速度初始化的表达式为

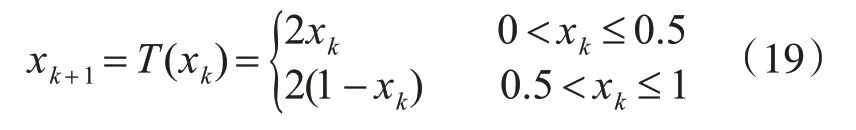
当xk=0，0.25，0.5，0.75或xk=xk-m（m=1，2，3，4）则使用如下公式：

根据式（4）和式（5）产生混沌向量β（k，i）（k=1、2、3∙∙∙N－1；i=1、2、3、∙∙∙m），然后将获得的混沌变量映射到变量取值范围，得到第k粒子第i维的值，映射公式如下：

本文遗传粒子两种算法的融合基本思路：利用粒子群法对获得的初步解进行局部搜索寻优，以获得局部最优解，再将获得的局部最优解传递给遗传算法进行选择、交叉、变异操作以进行全局寻优。

5 经济调度分析实例

本文以四台火力发电机组（G1，G2，G3，G4）、一个风力发电站（GW）和一个太阳能发电站（GG）组成的异质多能源发电系统为例，对本文提出的计及预测误差影响的电力系统经济调度模型的实用价值进行验证。选取某地区某日的数据进行计算分析，日负荷曲线如图1所示。火力发电机组的相关参数如表1所示。风力发电站的装机容量为80MW，太阳能发电站的装机容量为60MW，风力发电在各风速段的出力预测误差分布情况如表2所示，太阳能发电在各时段的出力预测误差分布情况如表3所示。

表1 火力发电机组相关参数

表2 风力发电出力预测误差分布情况

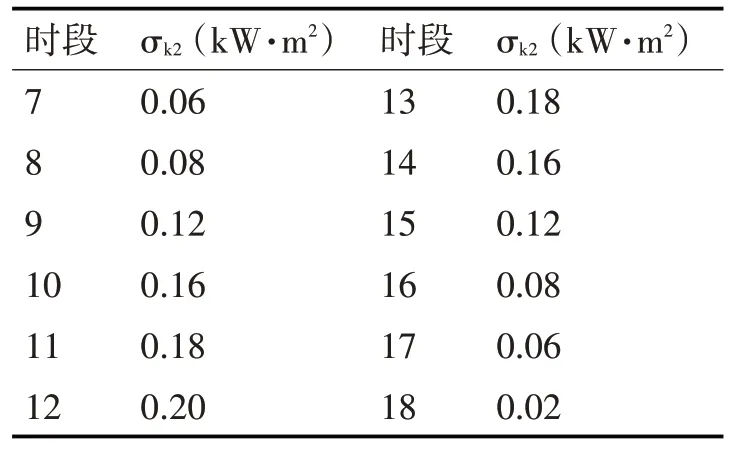
表3 太阳能发电出力预测误差分布情况

图1 某地区日负荷曲线图

采用本文改进的遗传粒子群算法对计及预测误差的经济调度模型目标函数进行优化分析，得到的计及预测误差影响的各时段机组出力情况如图2所示。为验证本文计及预测误差影响模型的有效性，同时对无光无风和不计及预测误差的运行方式进行计算分析，得到的计及预测误差和不计及预测误差的风力和太阳能机组出力情况如图3所示，不同方式下的运行成本如表4所示。

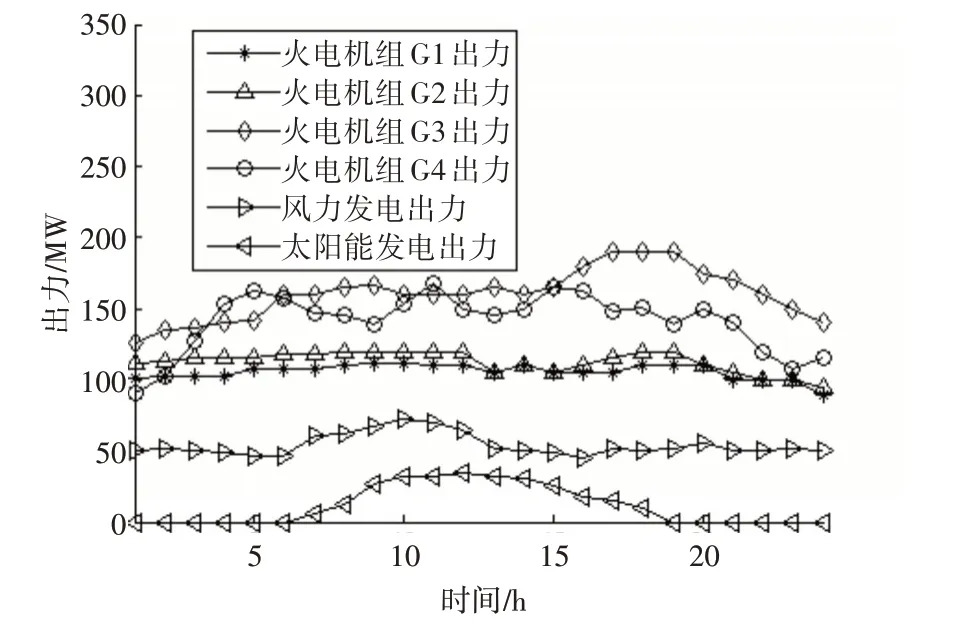
图2 各机组出力情况图

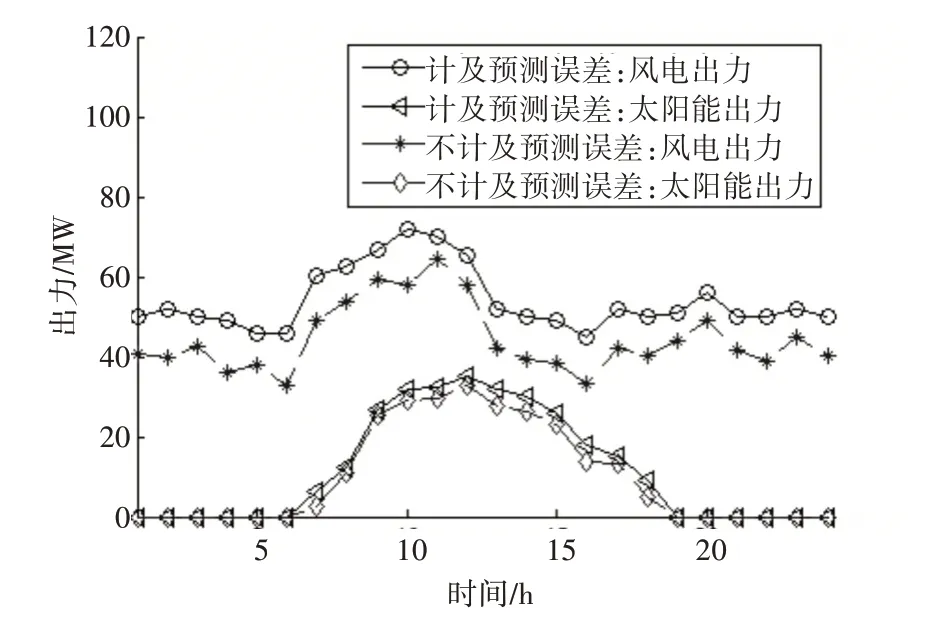
图3 风光机组出力情况图

表4 不同方式下的运行成本

根据经济调度模型优化结果可知，计及预测误差影响和不计及预测误差影响时，电力系统各发电机组的出力情况有所不同，风力和太阳能的发电出力均有所增加，表明计及预测误差影响时可以增大风力和太阳能的出力，提高了风光清洁能源的消纳能力，同时计及预测误差影响时可有效降低发电总成本，计及预测误差影响的总成本要比无光无风时降低约7.22%、比不计及预测误差影响时降低约2.18%，本文计及预测误差影响的经济调度模型具有很好的优越性。

6 结语

为使得风能和太阳能等清洁能源得到更好的发展和利用，在对风能和太阳能出力预测误差分布情况进行分析的基础上，本文提出了一种计及风能、太阳能出力预测误差影响的风能、太阳能和火力异质多能源电力系统经济调度优化模型，并建立了包含风能、太阳能和火力发电的仿真计算模型，结果表明本文计及预测误差影响的经济调度模型可以增大风力和太阳能的出力，提高风光清洁能源的消纳能力，同时还可以有效降低系统的发电总成本，计及预测误差影响的总成本要比无光无风时降低约7.22%、比不计及预测误差影响时降低约2.18%。本文方法可为包含风能和太阳能的电力系统经济调度提供有效的参考和技术指导。