石墨烯纳米复合材料热膨胀特性分析综述
孙晋媛
(西安医学院,陕西西安710021)
近年来,科学技术的迅速发展,特别是尖端科学技术的突飞猛进,不断考验材料的各种性能并对其提出越来越高、越来越严和越来越多的要求。相对于传统的单一材料,复合材料具有较强的可塑性,将不同的材料通过不同的制备工艺,可特定增强其某一性能或得到综合性能更加优异的材料。高分子基纳米复合材料是复合材料中的一种,由基体相和填充相两部分组成,一般,基体相为树脂、橡胶等高分子材料,填充相为碳纳米管、石墨烯等纳米材料[1]。
其中,纳米增强材料所具有的纳米尺寸效应和特殊的力学性能使高分子基纳米复合材料有着比其它复合材料更加优异的综合性能,在体育器材、航天航空、船舶、车辆制造、电器设备等领域都已呈现出广泛的应用前景。在体育器材领域,如跳高撑杆,大都会采用50%以上的复合材料,提高其综合性能短时间内产生较大变形以吸收冲击能,后又可复原,即在大变形下能保持弹性。当高分子基纳米复合材料涉及到温度波动较剧烈的使用环境时,很容易产生残余热应力和热变形,从而破坏材料的结构。尤其应用于精密仪器领域时,微小的变形就会破坏仪器的精密程度,最终影响其使用寿命。但是,当材料填充热膨胀系数较低或负热膨胀系数的材料时,材料整体的热膨胀系数会降低,热学性能得到改善[2]。因此为了纳米复合材料更好、更广泛地应用于各个领域,则要求知晓纳米复合材料的热膨胀特性,并且寻求更好的纳米填充材料,降低高分子基纳米复合材料的热膨胀系数,提高其热学性能。
1 理论综述
1.1 石墨烯纳米复合材料
石墨烯是一种由碳原子以sp2杂化形成的六方蜂巢晶格状的二维碳纳米材料,在经过包裹、卷曲、堆叠后,可以分别形成零维富勒烯(C60)、一维碳纳米管和三维石墨,所以石墨烯也被称为“碳材料之母”。石墨烯特殊的单原子层结构使其具有高强度、高比表面积、低比重、小尺寸效应和界面效应等特殊性能,且相对于之前研究比较火热的碳纳米管,其制作成本更低,且在制造过程中不容易出现团聚及分散不均匀等现象。因此石墨烯在作为增强填充材料、储能材料、吸附材料和超导材料等时有着更为显著的优势。
在温度升高的过程中,石墨烯的热变形同时存在着膨胀和收缩,膨胀的原因很普遍,主要是因为碳原子之间的键长增加,但同时碳原子会向石墨烯二维结构以外扩展,微观下变为三维结构,形成表面褶皱,产生石墨烯受热收缩的现象。该情况也同样存在于低温环境下,虽然石墨烯宏观上看似平整,但细观上其表面是褶皱的,褶皱的产生是为了保证石墨烯在温度骤变环境中的结构稳定性。温度的升高会使石墨烯褶皱的程度提高,出现受热收缩的现象。通过分子动力学研究了石墨烯的热膨胀系数,结果显示,在0~1200 K温度范围内时,石墨烯的碳原子向外扩展的程度大于其键长增加的程度,其表面褶皱始终占主导,所以热膨胀系数在该温度范围内为负值。
纳米复合材料是以高分子或金属为基体,在基体中填充适量的纳米材料,通过特殊的方法制备出的具有优异性能的复合材料。该复合材料发挥了纳米填料的纳米尺寸效应,将纳米填料所具备的机械、热力学和电学等性能与基体材料本身所具有的可加工性能好、耐腐蚀、固化效果优良等优点相互融合,使复合材料的整体宏观性能得到较大的提高。石墨烯负热膨胀特性使其在改良复合材料热学性能方面成为十分重要的纳米填料,填充少量的石墨烯可有效地降低复合材料的热膨胀系数,提高其热稳定性。
1.2 热膨胀系数
纳米复合材料作为宏观均匀但细观非均匀介质,其有效性质的研究多采用细观力学进行分析。代表性体积单元法是复合材料细观力学分析中最直接且有效的方法,而对于复合材料热膨胀特性的细观力学研究,即采用“均匀化”的思想,将复合材料整体的热膨胀行为通过各个组分的材料性质来体现[3]。
对于石墨烯纳米复合材料,石墨烯作为夹杂体,在基体中难以分散均匀,且石墨烯的大小、形状、方向不一致,难以对其建立一个完善的理论模型。因为分散在基体中的石墨烯的形状为不规则的片状夹杂,其Eshelby张量不均匀,即在均匀外载下,夹杂内部的弹性场不均匀。因此,将石墨烯的形状理想化,看作内部弹性场均匀、长径比很小的扁椭球形夹杂,便于整个理论模型的简化。如图1所示,将石墨烯作为扁椭球形夹杂,基体材料作为包裹,再将基体与夹杂组成的二相胞元放置于一个无限大的等效介质中,建立广义自洽模型。

图1 石墨烯纳米复合材料热膨胀系数理论模型建立流程图Fig.1 The flow chart of the theoretical model of thermal expansion coefficient of graphene nanocomposites
在广义自洽模型的基础上,令其边界上受到的远场均匀载荷,而使环境温度改变。此时若采用等效夹杂理论,本征应变不光包括相应变,还包括因基体与夹杂的热膨胀系数不同所导致的热失配应变。通过广义自洽模型,我们可以得到二相胞元的纵向和横向热膨胀系数,再通过应力应变换轴公式,将材料的热膨胀应变变为所有二相胞元的热膨胀应变对某一轴向取随机角度的均值。因此,石墨烯纳米复合材料最终可以简化为扁椭球形二相胞元随机分布在等效介质中的三相模型[4]。
2 研究结果综述
纳米复合材料的热膨胀率也近似为不同斜率的直线,即在30~100 ℃,其热膨胀系数为一常数。图2 是所采用的理论研究方法评价的质量分数为1.0%~5.0%的石墨烯/环氧树脂纳米复合材料的热膨胀系数,其趋势与Shapery方程和Schneider方程的评价结果相似,纳米复合材料的热膨胀系数随石墨烯含量的增加而不断降低,但降低的趋势越来越小。说明石墨烯的增强效果会受到其含量的限制,当石墨烯的含量达到某一值时,该纳米复合材料的CTE不再随着石墨烯含量的增加而降低。评价结果还显示,当石墨烯含量为5%时,该纳米复合材料的CTE降低了31.2%。虽然与Schneider方程的石墨烯的增强效果不相上下,将石墨烯的形状看作扁椭球形,而不是纤维状,更接近石墨烯真实的形状[5-6]。

图 2 石墨烯纳米复合材料的热膨胀系数(30~110 ℃)Fig.2 Thermal expansion coefficient of graphene nanocomposites
由图3 可知,长径比在0~0.1范围内时,该纳米复合材料的热膨胀系数随长径比的增大而增大。长径比对评价结果影响会受到自身的限制,其在0~0.1范围内时的影响程度明显大于0.1~1范围,ρ=0.1相对于ρ=0的纳米复合材料,其CTE增大了29.2%,而ρ=1相对于ρ=0.1的纳米复合材料,其CTE只增大了3.4%。石墨烯片很薄,但片层的重叠会导致长径比增大,影响填充后纳米复合材料的热膨胀特性,所以在制备石墨烯及其纳米复合材料时,应尽量使石墨烯较好的剥离,获得较小的长径比[7]。

图3 石墨烯3%纳米复合材料的热膨胀系数Fig .3 Thermal expansion coefficient of graphene 3%nanocomposites
3 石墨烯纳米复合材料热膨胀特性
石墨烯纳米复合材料的细观模型十分复杂,一般的建模软件难以实现。Digimat软件主要针对于多尺度复合材料结构预测及建模分析,所以其在复合材料的细观建模方面更为简单、更具优势,但其自带的求解器求解能力较弱。因此采用ABAQUS与Digimat联合进行数值模拟,通过Digimat的FE模块,建立石墨烯/环氧树脂纳米复合材料的细观RⅤE模型,并施加相应的边界条件和载荷,再将模型导入ABAQUS,利用其强大的求解能力进行仿真分析[6]。最终,可得到石墨烯含量为1%~5%的纳米复合材料在30~110 ℃温度范围内的热膨胀仿真结果,同时分析石墨烯的尺寸大小、长径比、取向分布和团聚对其的影响。
3.1 仿真分析
在Digimat中需定义填料的形状尺寸,石墨烯是一种无固定形状的二维纳米材料,计算模型将其简化为长径比ρ=0.001的扁椭球形。扁椭球形具有曲率较大的过渡边,且在RⅤE的边缘处易产生形状极不规则的夹杂,不利于网格的划分。薄圆柱片与扁椭球形外形相似,但其结构更简单,截面形状多为规则的四边形,网格划分也更容易。由于Digimat软件的限制,石墨烯的含量越大,其长径比的大小就越受限制。当石墨烯的含量为5%时,其长径比至少为0.024时,才能建模成功。当石墨烯的形状尺寸固定时,RⅤE中片数规模会随石墨烯质量分数的增加而增大。由于石墨烯是随机分布的,片数规模小时,分布均匀性弱,得到的结果便不稳定;片数规模大时,结构复杂性高,模型计算时间长。因此,在保证计算效率的前提下,每个模型必须有足够规模的片数,且至少大于50片。当石墨烯的质量分数和长径比一定时,片数规模由薄圆柱片的直径决定。因此,为了得到计算效率高、稳定收敛的结果,令石墨烯的直径为0.2。此时,当石墨烯含量为1%~5%,其片数规模为69~343,该范围内的片数规模对结果影响微弱,可忽略不计,较为合理。综上考虑,最终将石墨烯简化为直径为0.2,长径比为0.024的薄圆柱片[7-8]。
石墨烯的形状尺寸确定后,在Digimat-FE模块分别建立石墨烯含量为1%~5%的石墨烯/环氧树脂纳米复合材料的RⅤE模型(图4(a)),再对模型进行网格划分(图4(b)),同时施加周期性边界条件和温度载荷。最后,将模型导入ABAQUS进行仿真计算,得到石墨烯/环氧树脂纳米复合材料在110℃的温度载荷下的热膨胀如图5所示。

图4 RVE模型(3%)Fig.4 RVE Model (3%)

图5 热膨胀云图(3%)Fig.5 Thermal expansion cloud (3 %)
数值模拟结果显示,与混合定律、Kerner方程、Wang&Kwei方程、Chow方程类似,该纳米复合材料的热膨胀系数与石墨烯含量之间几乎满足线性关系,CTE随着石墨烯的含量的增加而不断降低。但石墨烯在数值模拟结果中的增强效果更好,当石墨烯的含量为5%时,该纳米复合材料的CTE降低了31.3%。
3.2 影响因素分析
石墨烯纳米复合材料的热膨胀系数的影响因素众多,现统一石墨烯的含量为1%,形状为薄圆柱片,分析讨论石墨烯的尺寸大小、长径比、取向分布和团聚四个方面的影响。在温度载荷达到30℃、40℃、50℃、…、110℃时,每个模型针对每个温度载荷,都会得到三个方向的变形量,分别计算每个方向上的热膨胀系数,取平均值作为该模型模拟的有效热膨胀系数,并计算三个方向上的偏差。
(1)石墨烯的尺寸大小
石墨烯的含量为1%时,若将石墨烯的形状统一为薄圆柱片,则其尺寸大小可用圆柱片的直径d表示,同时其长径比可取更小为0.01。考虑到石墨烯片数规模的影响,分别建立圆柱直径为0.15、0.18、0.20、0.22和0.25的RⅤE模型。图6为圆柱片的直径为0.15~0.25范围内的石墨烯/环氧树脂纳米复合材料的CTE,结果显示石墨烯在该范围内的尺寸大小变化对其填充材料的CTE影响不大。但尺寸大小的变化影响了模型中石墨烯的片数规模,随着石墨烯尺寸的增大,其片数减少,分布均匀性减弱,导致x、y、z三个方向的热膨胀值的差别也愈加明显,从而对最终结果产生了微弱的间接影响。

图6 石墨烯尺寸大小的影响(ρ=0.01)Fig .6 Effect of size of graphene (ρ=0.01)
(2)石墨烯的长径比
石墨烯的尺寸大小对其填充材料的CTE影响不大,所以为了得到较大片数规模的石墨烯,选取石墨烯的尺寸大小d=0.15,分别建立长径比为0.01、0.02、0.03、0.04和0.05的石墨烯/环氧树脂纳米复合材料的细观RⅤE模型,可得到较为稳定的结果,如图7所示。可以看出,石墨烯纳米复合材料的热膨胀系数随着长径比的增大而增大。石墨烯片层的堆叠和片径尺寸的减小是导致CTE增大的两个主要因素,所以为得到热膨胀性能更好的石墨烯纳米复合材料,应使石墨烯更好地剥离、分散在基体材料中的同时,保证其尺寸的完整性。

图7 石墨烯长径比的影响(d=0.2)Fig.7 The effect of graphene aspect ratio (d=0.2)
(3)石墨烯的取向分布
石墨烯的取向分布是纳米复合材料内部一个十分重要的显微特征,影响材料的统计均匀性,可能使其在宏观上变得各向异性。令石墨烯的长径比为0.01,薄片直径为0.2,分别建立取向分布为3D随机、2D随机、与y、z轴定向呈90°和45°的四种RⅤE模型,如图8所示。
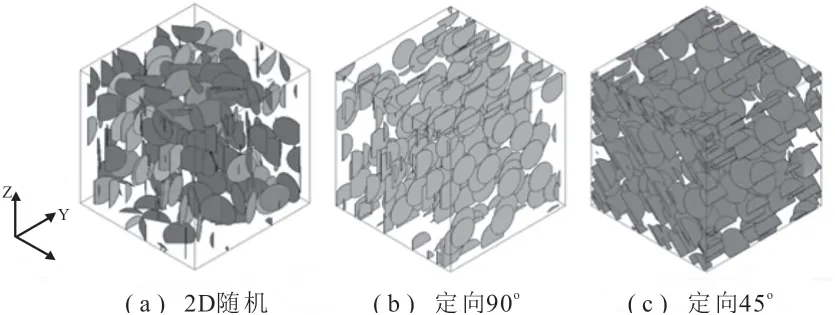
图8 石墨烯的取向分布Fig.8 Orientation distribution of graphene
图8 显示了模型分别在x、y、z方向上的线热膨胀系数和其平均值,由图可知,尽管石墨烯的取向分布不同,但其均能有效降低填充材料的CTE,只是降低程度不同。石墨烯随机分布的纳米复合材料在三个方向的CTE的差别较小,特别是3D随机分布,其具有宏观各向同性,综合热膨胀性能也相对较好。而石墨烯的定向分布破坏了该纳米复合材料的统计均匀性,使其变得各向异性,三个方向上的CTE差异较大,综合热膨胀性也较弱。薄圆柱形夹杂具有二维约束,不同于具有三维约束的球形夹杂,与具有一维约束的纤维状夹杂类似,当其定向分布在基体中时,复合材料将不再具有统计均匀性,x,y,z三个方向上的CTE具有明显差异。
3 结语
上述理论研究评价了石墨烯纳米复合材料的热膨胀系数,并分析了石墨烯的含量、长径比等诸多影响因素,可知:当石墨烯的长径比越小,分散程度越高时,其增强效果越好,可得到热学性能更加优异的石墨烯纳米复合材料。因此,在制备石墨烯纳米复合材料时,应使石墨烯在基体中较好地剥离、分散,且保持片层的完整性。石墨烯作为填充物,可有效降低纳米复合材料的热膨胀系数,且随着石墨烯含量的增加,热膨胀系数不断降低,有利于减小残余热应力和热变形。有些体育器材使用常年在外放置,环境高温等都会对材质有很大的影响。因此为了纳米复合材料更好、更广泛地应用于体育器材等各个领域,则需要了解纳米复合材料的热膨胀特性,并且寻求更好的纳米填充材料,降低高分子基纳米复合材料的热膨胀系数。

