利用等频面分析各向异性晶体的双折射

张利伟，李 娟

（安庆师范大学数理学院，安徽安庆 246133）

光学是一门既古老又年轻的学科，是物理学中一个重要的分支，是研究光的本性、光的传播以及光与物质相互作用规律及其应用的科学。光学与信息科学、生命科学、精密机械与制造和微电子技术等领域密切交叉和相互渗透，光学工程以及光学产业的发展很大程度上推动了社会和科技的进步，例如，利用晶体的双折射效应可以设计出各种晶体光学器件，其中有许多是由多块光轴取向不同的晶体级联构成的，如偏振分光镜、波片、渥拉斯顿棱镜等，利用弧形波晶片还可以产生矢量光束实现强聚焦特性[1]。晶体的双折射现象是指当一束光由各向同性介质入射到各向异性晶体表面时，在晶体内产生两束折射光的现象[2]。晶体的双折射主要是由于晶体结构的各向异性造成的，与构成晶体的原子晶格结构密切相关。有些晶体的晶格结构属于单轴各向异性，有些属于双轴各向异性。晶体材料结构的特殊性质导致了各向异性的电学、光学等特性，比如弹性系数、热膨胀、导热、电导率等。这些各向异性性质在偏振光电器件、偏振热电器件、偏振光探测器等领域有重要的应用。这里我们主要讨论各向异性晶体界面处的双折射问题。单轴各向异性晶体中的双折射最早由惠更斯借助波面作图法进行了解释，此方法虽简单易解，但缺乏系统的理论支撑，学生对这部分内容理解得不深不透。对于单轴晶体和单轴晶体的界面来说，相对比较复杂，可以出现双折射双反射性质，宋哲等人通过作图法进行了分析[3]。为了加深学生对双折射物理图像的理解，本文从光波的电磁理论出发，通过推导光波在各向异性介质中传播的色散关系，利用等频面的方法对各向异性晶体界面处的双折射进行直观地分析和模拟，这种具有理论支撑的方法不但能分析单轴各向异性晶体的双折射，还能分析双轴各向异性晶体以及光轴与坐标轴有任意夹角的情况，此外，借助等频面还能直观地解释超材料的反常折射、反射性质[4-5]。

1 光在各向异性介质中传播的色散关系

各向异性介质的介电常数ε为二阶张量（非磁性介质），为了简单起见，采用对角化的形式，在笛卡尔坐标系中

其中，当εx≠εy≠εz时，称为双轴各向异性介质；当εx=εy≠εz时，称为单轴各向异性介质；当εx=εy=εz时，介质则退化为各向同性。介质中传播的平面波的电场形式为E=E0ei(ωt-k·r)，磁场为H=H0ei(ωt-k·r)，根据麦克斯韦方程组[D]=[ε][E]，∇×H=jωD和∇×E=-jμH很容易推导出角频率为ω的平面波在各向异性介质中传播时满足的色散关系[6-7]：

对一定角频率，满足式（2）的波矢构成的面就是等频面，kx、ky和kz分别为波矢的x分量、y分量和z分量。

这里主要考虑各向同性介质与单轴各向异性晶体界面双折射的情况。假设一平面波从空气斜入射到单轴各向异性介质中，x-y平面为界面，z轴为光轴，垂直交界面，则各向异性晶体中x-z平面内光波满足的色散关系为

kx和kz满足的曲线就是等频线，kx=k0sinθ，k0=ω/c，θ为入射角。从时间平均坡印亭矢量的定义S=可得，

E0′和H0′分别为折射光的电场、磁场振幅，折射波矢的z分量kz的正负符号选取要保证能量远离界面，能量折射角θs=arctan(Sx/Sz)。另外，根据电磁场边界条件可得界面处o光和e光的反射系数为

2 单轴各向异性晶体界面的折射

为了直观地分析各向异性介质中的双折射，首先计算非磁性单轴各向异性晶体中两种光波的等频面，这里选择e 光主轴折射率是o 光主轴折射率的两倍，kx、ky和kz相对于k0进行了归一化，如图1（a）所示。很显然，等频面是个双层面，椭球面代表的是e光的等频面，球面代表的是o光的等频面。根据各向异性介质介电常数张量和磁导率张量的取值，其等频面会有更复杂的形状[6]。现在考虑空气与单轴各向异性晶体界面的折射情况(ɛx=ɛy)，分界面为x-y面，z＞0为单轴晶体，z＜0为空气，x-z面是入射面，如图1（b）所示。θin为入射角，θo和θe分别为o光和e光的能量折射角。根据式（3）计算出空气中光波传播满足的等频线是圆，如图1（c）中的点线圆所示，单轴各向异性晶体中o光和e光的2维等频线，分别对应圆和椭圆，这里取ɛx=ɛy=4，ɛz=1.5。根据电磁理论，电磁波的能量传播方向与群速度∇k(ω)k相同，这意味着群速度与等频面垂直[8]，即光束在波矢面上任一点的传播方向为该点切线的法线方向。根据边界处电磁场的切向分量连续的性质，界面两侧的入射波矢和折射波矢的x分量相等。基于这些基本规则，就可借助等频面定性、定量地分析各向异性晶体中的o 光和e 光的折射。

图1 （a）单轴各向异性晶体中o光和e光的3维等频面示意图；（b）空气与单轴各向异性晶体的界面折射；（c）单轴各向异性晶体中o光和e光的等频线，不同颜色的箭头线分别代表入射光，o光折射和e光折射

在一定的入射角θ下，入射波矢的x分量kx=k0sinθ，当θ=30°时，kx/k0=0.5，如图1（c）中的竖直点线所示。根据光波在界面上相位相等的条件，o光和e光的折射光的x分量也应该是0.5k0。这条kx=0.5k0的竖线分别与空气中光的等频线，o 光和e 光的等频线相交于a(a′)，b(b′)和c(c′)点。由于入射波沿z轴正方向，所以只能通过在a、b和c三点处分析其入射和折射情况。连接坐标原点与a点的矢量就代表入射光，其与z轴之间的夹角也就是入射角。在b和c点作垂直于等频线且指向传播方向的矢量就是o 光和e 光的折射光，它们与z轴之间的夹角也就是o光和e光的折射角。从图1（c）可以看出，o光和e光折射角不同，并且会随着等频线形状的变化而改变，也就是随着各向异性介质主轴介电常数和磁导率的不同而发生变化。

图2（a）是单轴各向异性晶体界面o光和e光在不同入射角下的能量折射角，从图中可以看出，无论是o光还是e光，其能量折射角的值均随着入射角的增大而增大。根据式（2），发现o光的等频面与ɛz无关，只由ɛx和ɛy决定，而e 光的等频面与ɛz有很大的关系。在图2（a）中，保持ɛx=ɛy=4 不变，分别取ɛz为1.5、2、2.5，发现随着ɛz的增加，e 光的折射角逐渐减小。对于这样的单轴各向异性介质界面，其反射率随着入射角也会有所不同。图2（b）是ɛx=ɛy=4，ɛz=1.5条件下，o光和e光的界面反射率，可以看出，o光的反射率随着入射角的增大而增大，而e 光的界面反射率随着入射角的增大先减小后增大，在满足布鲁斯特角时会出现零反射。

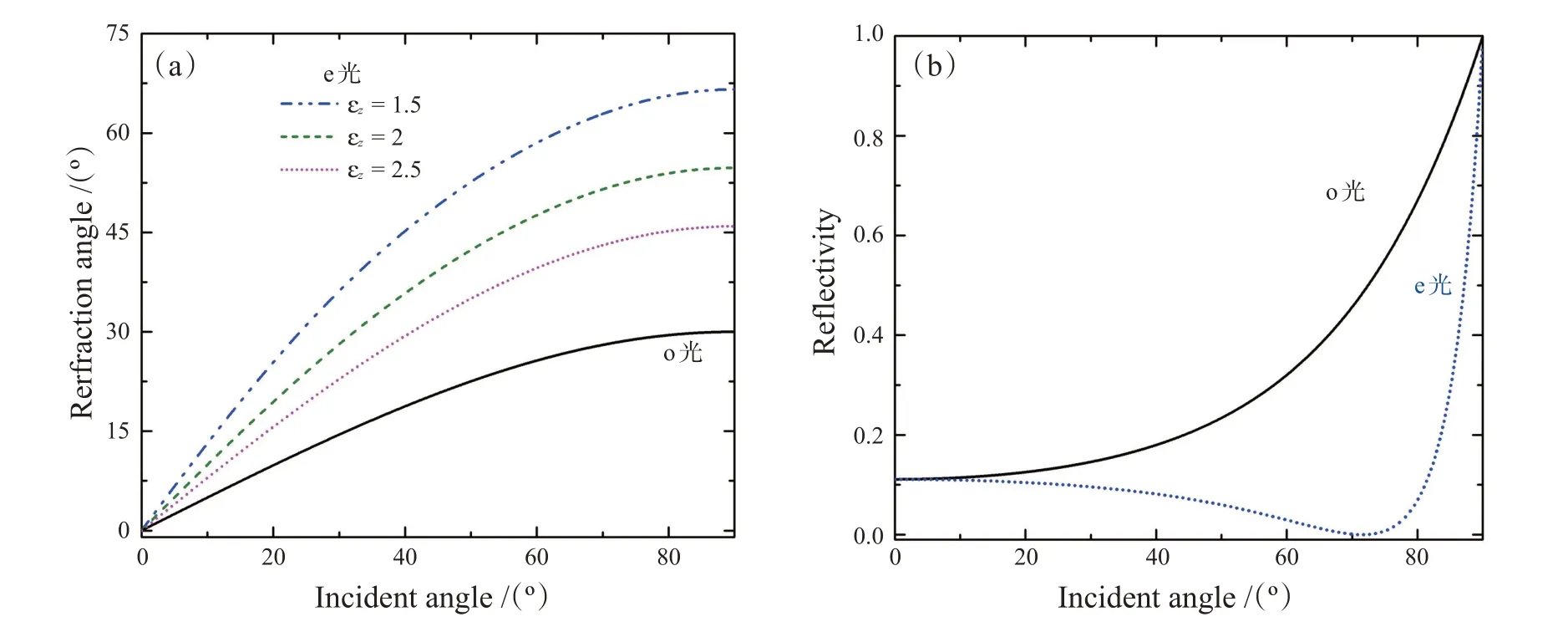
图2 （a）单轴晶体界面o光和e光的折射角与z轴介电常数的关系；（b）ɛz=1.5，ɛx=ɛy=4，o光和e光的界面反射率

为了直观地理解双折射的物理图像，对30°入射角的o光和e光的界面折射情况进行了电磁仿真模拟。图3（a）和（b）分别是使用电磁仿真软件Comsol进行模拟的e光和o光折射的场分布情况，白色箭头线和蓝色箭头线分别代表入射和折射光。很显然折射电磁场和入射场分别处在法线的两侧，说明为正折射，并且e光和o光的折射角分别是35°和14°，与理论分析也非常的吻合。

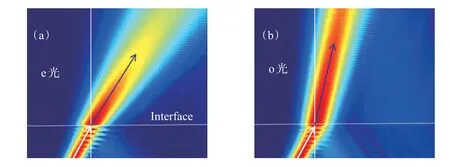
图3 （a）和（b）分别是模拟的e光和o光折射的场分布情况，其中ɛz=1.5，ɛx=ɛy=4，入射角为30°

3 超材料界面的折射性质

在前面的讨论中，无论是e光或o光，晶体的主轴介电常数和磁导率都是正值，所以其3维的等频面是椭球面，2维的等频面是椭圆。随着光学的发展，一些具有奇异特性的超材料在实验上制备出来。超材料[9]是指一些具有天然材料所不具备的超常物理性质的人工复合结构，多是一些亚波长金属或介质微结构，通过局域共振机制或米氏散射机制实现了任意的有效介电常数和有效磁导率，从而导致新奇的光调控能力，如负折射、超分辨成像、隐身、场局域和增强自发辐射等[7,10]。由于奇异的电磁性质和应用，超材料成为国际上光学、凝聚态物理、信息科学等学科的前沿研究领域，不但可以调控光的全吸收、全透射和反射相位等，而且可以调控空间场的分布。对于超材料来说，介电常数和磁导率的张量参数可以具有不同的符号（正或负）和数值，在应用上具有很大的灵活性。这里考虑超材料的磁导率也是各向异性的，取ɛz=1.5，ɛx=ɛy=4，μx=μy=1，μz=-1，很显然这是一个单轴各向异性材料，根据式（2）和（3），可以计算e光和o光的3维和2维等频面。图4（a）是这一单轴各向异性超材料中o光和e光的2维等频线，o光的色散关系为一双曲线，透射波的波矢＞0总是成立的，e光的色散关系为一椭圆，其中红色点线代表空气中光波的等频线。根据能流公式（4）中So的表达式，需要选择双曲线的上半支(kz＞0)以保证能量沿z方向传播。根据前面介绍的判断能量折射的方法，就可画出e光和o光的折射情况。

在图4（a）中不同颜色的箭头线分别代表入射光、o光折射和e光折射，在一定入射角下，e光具有正的能量折射角，而o光总是具有负的能量折射角。图4（b）是空气和单轴各向异性超材料界面处o光和e光不同入射角下的能量折射角，无论是o 光还是e 光，其能量折射角的值均随着入射角的增大而增大。为了直观地印证这一点，对30°入射角的情况进行了电磁仿真模拟。

图4 （a）单轴各向异性超材料中o光和e光的2维等频线，点线代表空气中光波的2维等频面，不同颜色的箭头线分别代表入射光、o光折射和e光折射，垂直点线代表的是30°入射角；（b）单轴各向异性超材料界面o光和e光在不同入射角下的能量折射角，其中，ɛz=1.5，ɛx=ɛy=4，μz=-1

图5（a）和（b）分别是模拟e光和o光折射的场分布情况，可见折射角分别是35°和-14°。根据超材料主轴介电常数和磁导率的取值情况，超材料界面会出现o光或e光的全反射、全透射和负折射，此外双轴各向异性介质界面的复杂折射情况也可以借助等频面进行直观地理解和分析。

图5 （a）和（b）分别是e光和o光折射的场分布，其中ɛz=1.5，ɛx=ɛy=4，μz=-1，入射角为30°

4 结论

综上所述，本文主要利用等频面分析了单轴各向异性介质界面处的光学反射与折射性质，计算了e光和o光在单轴各向异性晶体中的折射情况。在理论分析的基础上，利用电磁仿真软件对各向异性介质中光的双折射场分布进行了模拟。利用等频面方法还分析、计算了双曲色散超材料中的负折射，使学生对光学前沿课题有所了解。这种采用等频面分析与软件模拟相结合的方法，加深了学生对双折射物理图像的深刻理解，激发了学生的学习兴趣，提高了课程教学效果。