调频广播外辐射源雷达中的目标方向估计方法

宋 聪，黎 杨*，2

1.武汉工程大学电气信息学院，湖北 武汉430205；2.湖北省视频图像与高清投影工程技术研究中心，湖北 武汉430205

近年来，基于第三方非合作辐射源的外辐射源雷达系统，由于具有潜在的隐蔽、反隐身目标和抗干扰等特性，受到了特别关注［1-2］。外辐射源雷达利用第三方非协作辐射源进行目标探测，由于其本身不发射信号，因此相对于传统的有源雷达，具有很多的优势，如成本低、体积小、对电磁环境无污染和具有探测隐身目标的潜力等［3］。

目前，多种外辐射源信号被用做无源探测，如调频（frequency modulation，FM）广播信号［4］、移动通信基站［6］、数字/模拟电视信号［5］等。FM广播信号具有站点多、覆盖范围广、组网潜力大、模糊函数距离分辨率高等优点，被认为是最适合用于无源探测的辐射源之一［7］。

在外辐射源雷达中，天线接收微弱的目标散射波信号，同时还会接收到很强的直达波、多径和杂波干扰。由于散射波的信噪比（signal-to-noise ratio，SNR）通常极低（接收到散射波的SNR典型值约为-40 dB左右），同时还存在很强的直达波干扰（直达波与散射波的功率之比的典型值大于90 dB）［8］，散射波的波达方向（direction-of-arrival，DOA）估计问题是一个极强干扰、极低信噪比情况下的DOA估计问题。

近几十年来，出现了很多的算法用于估计信号DOA，例如：多重信号分类（multiple signal classification，MUSIC）［9］、旋转不变子空 间（estimation of signal parameters via rotational invariance technique，ESPRIT）［10］，以及各种特殊应用场景的方法［11］等。然而，现有方法很少能适用于微弱信号DOA估计。在微弱信号DOA估计方面，文献［12］提出了一种基于软稀疏表示的DOA估计方法，该方法基于稀疏性的前提下，应用迭代加权最小方差法求解软稀疏解，最后估计目标方位。文献［13］提出了一种协方差矩阵的重构方法，该方法能够明显地提高协方差矩阵的信噪比，将新的协方差矩阵应用到最小方差无畸变响应算法进行DOA估计，改善了低信噪比条件下的DOA估计性能。文献［14］提出了一种适用于低信噪比场景的正交线性预测传播算子算法（orthogonal propagator method-linear prediction，OPM-LP）方法，该方法利用线性预测原理，重构降噪的数据协方差矩阵，然后使用正交传播算法进行DOA估计，但是该方法不适用于-40 dB极低信噪比情况。尽管上述方法一定程度上能够估计微弱信号的DOA，但并不适用于本文信噪比极低，同时还存在很强的直达波干扰的应用场景。

在外辐射源雷达目标散射波估计方面，文献［15］提出了一种利用四元Adcock天线阵列测量目标散射波DOA估计方法，该方法预先计算每一个通道的接收信号与参考信号的互模糊函数，在距离多普勒图上消除了直达波、多径和杂波干扰之后，再利用成对监视信号之间的角度关系估计回波方向，但是该方法依赖于特定的Adcock天线阵列结构。文献［16］提出了一种适用于外辐射源雷达的比幅测角方法，该方法利用八单元均匀圆阵天线结合方向图综合技术形成覆盖全空域的18个波束，用以对目标进行扫描。文献［17］使用了2个监视天线，通过计算距离-多普勒图上的相位差来估计目标散射波。尽管上述方法在应用中能获得一些强目标的方向，但是依赖于特定的天线配置，并且其精度和分辨率均很低。

针对目标散射波的DOA估计难题，本文提出一种距离多普勒域阵列信号处理（range-doppler domain array signal processing，RD-ASP）方法，在估计其散射波的DOA之前增强期望散射波信号。“增强”一词意味着分别极大地提高了期望散射波信号的功率与直达波信号的功率、与干扰散射波信号的功率、以及与噪声的功率之比。该方法首先计算直达波信号与天线各个阵元接收信号之间的互模糊函数，然后在互模糊函数上抽取特定时差和多普勒的数据构建单个采样点虚拟阵列信号，再将单个采样点虚拟阵列信号扩展为多个采样点虚拟阵列信号，最后通过频率扫描的方式，用MUSIC算法进行空间谱估计得到二维DOA-多普勒图，最终可获得散射波的DOA，及其对应的多普勒频率。

1 问题描述

1.1 FM广播信号

FM广播信号一般由主信道信号、副信道信号和导频信号组成的立体声复合信号。主信道信号是左声道信号和右声道信号的和信号，副信道信号是左声道和右声道信号的差信号，导频信号是为了接收而传送的辅助信号。t时刻的立体声复合信号m(t)可表示为［18］：

1.2 阵列信号模型

考虑一个均匀直线阵列（uniform linear array，ULA），阵元为全向性天线。假设无同频干扰信号，接收信号由一个直达波和多个散射波组成。接收到的阵列信号x (k)可表示为：

其中k是采样点数；i=S表示直达波，i≥1表示散射波；ai，i=S,1,…,L是第i个信号的导向矢量；s(k)是时域中的直达波；ηi，τi和νi是第i个信号（相对于直达波）的幅度衰减，时差和多普勒频移；FS是采样率；n(k)表示噪声。x(k)，ai和n(k)的维数为M×1维，其中M表示阵元数。假定噪声是高斯白噪声。在本文中，阵列信号x(k)称为“实际阵列信号”。

1.3 MUSIC空间谱

MUSIC空间谱可表示为：

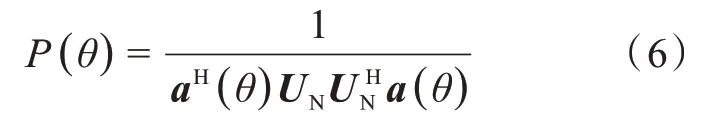
其中谱的峰值对应的角度θ为波达方向。

1.4 直达波参考信号获取

波束形成技术用于空间滤波。参考通道中的直达波信号由yR(k)=wHx(k)获得，其中wH是波束形成器指向直达波方向时的权矢量，可近似认为经过波束形成后yR(k)=s(k)。

1.5 模糊函数

雷达信号的模糊函数定义为：

其中τ表示时延，ν表示多普勒频移。模糊函数的一个性质是在A(0,0)处响应最大。

2 新方法介绍

2.1 虚拟阵列信号构建

参考信号yR(k)与第m个天线的接收信号xm(k)的互模糊函数表达式为：

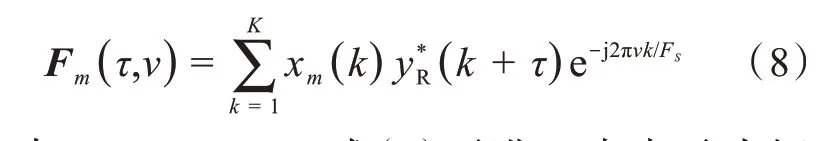
其中m=1,2…M。式（8）可进一步表示为矩阵形式的阵列互模糊函数F(τ,ν)：

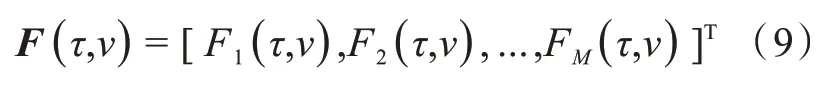
矩阵F(τ,ν)具有与实际阵列信号相似的形式，在本文中称为“虚拟阵列信号”。虚拟阵列信号F(τ,ν)具有3个虚拟信号分量：具有导向矢量aS的信号分量，称为“虚拟直达波信号”；具有导向矢量ai的信号分量，称为“虚拟散射波信号”；含n(k)的分量称为“虚拟噪声信号”。

假设一个期望散射波信号的导向矢量为a1，时差为τ1，多普勒频移为ν1，且yR(k)=s(k)，则虚拟阵列信号F(τ1,ν1)可以表示为：

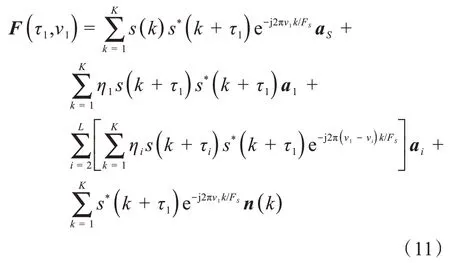
2.2 期望散射波信号的增强

因此，虚拟阵列信号δ的值比实际阵列信号大。

将虚拟期望散射波信号与虚拟干扰散射波信号的功率的比值定义为ε，则虚拟阵列信号F(τ1,ν1)的ε为：

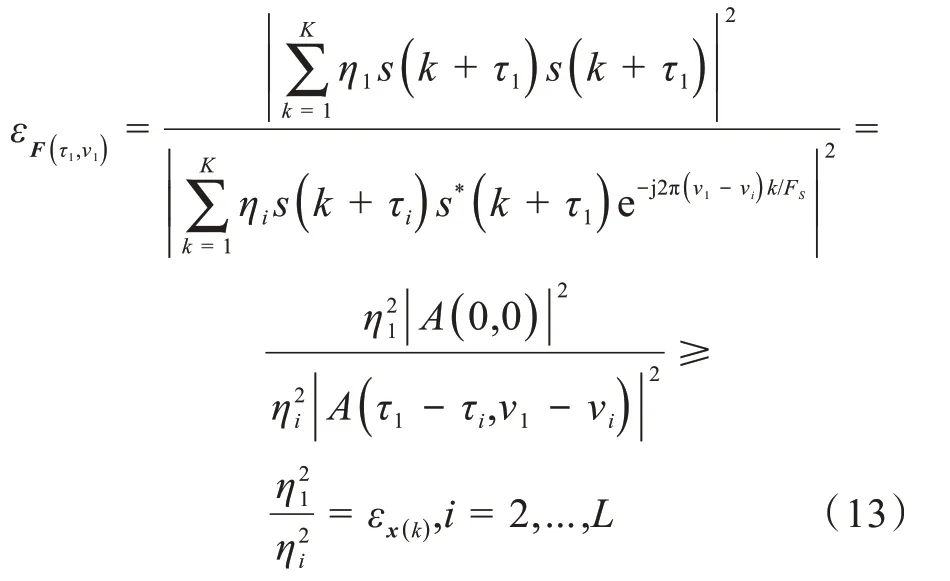
因此，虚拟阵列信号F(τ1,ν1)的ε比实际阵列信号x(k)大。

对于噪声，将虚拟期望散射波信号与虚拟噪声信号的功率比定义为γ，使用柯西-施瓦茨不等式可证明虚拟阵列信号F(τ1,ν1)的γ比实际阵列信号x(k)大。

其中PS是直达波信号的功率，PN是噪声的功率。

由式（12）～式（14）可知，导向矢量为a1的虚拟期望散射波信号经过式（11）处理后被增强了。从式（12）和式（13）可以看出δ和ε与模糊函数图形上的峰值到底平面的差有关，γ与处理时长有关，因此可以通过增加处理时间，进一步增强期望散射波信号。

然而式（11）中的虚拟阵列信号F(τ1,ν1)只有单个采样点，很难直接使用传统的DOA估计方法。下面将单个采样点的虚拟阵列信号扩展为多个采样点的虚拟阵列信号。将多普勒频移设定的区间范围(-νmax,νmax)均匀划分为Lν个点ν=linspace(-νmax,νmax,Lν)，对于频率νFix∈(-νmax,νmax)，可 以 获 得Lt个 矩 阵：F[t(1),νFix],F[t(2),νFix],…,F[t(Lt),νFix]，每个矩阵的维数为M×1，构建一个M×Lt维矩阵Gν：

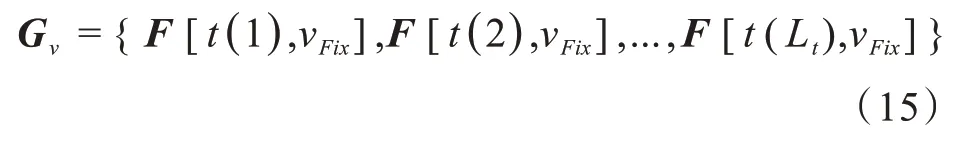
Gν矩阵被称为“多个采样点的虚拟阵列信号”。

2.3 散射波DOA估计

采用MUSIC算法进行空间谱估计。对于多个采样点的虚拟阵列信号Gν，其采样数据协方差矩阵可表示为：

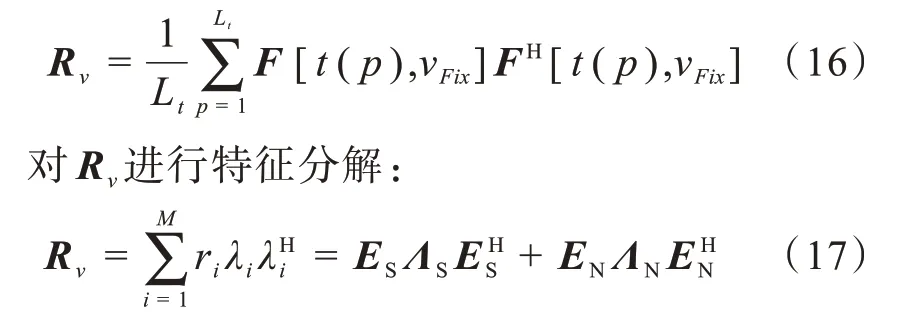
其中：ri和λi是Rν的特征值和对应的特征向量；特征值按降序排列，即r1＞…＞rd＞＞rd+1=…=rM；Rν的前d个大特征值对应的特征向量组成虚拟的信号子空间ES=[ λ1,…,λd]；剩下的M-d个小特征值对应的特征向量组成虚拟的噪声子空间EN=[λd+1,…,λM]。

最后用MUSIC算法进行空间谱估计：

其中P (θ,νFix)的峰值表示具有νFix频移信号的DOA。如果扫描所有多普勒频移区间，则可以获得所有散射波和直达波信号的DOA，以及它们对应的多普勒频移，最后可以组合得到DOA-多普勒频移图。

2.4 实现步骤

算法流程如图1所示，主要步骤总结如下：

步骤1：估计直达波信号的DOA：θS。

步骤2：对直达波方向进行波束形成，获得直达波信号yR。

步骤3：通过式（8）计算yR和每个天线接收信号的互模糊函数，然后将它们抽取组合构造单个 采样点的虚拟阵列信号F(τ,ν)，接着将多普勒频移设定的区间范围均匀划分为Lν个点v=linspace(-νmax,νmax,Lν)来构建多个采样点的虚拟阵列信号Gν。

步骤4：对多个采样点的虚拟阵列信号Gν应用MUSIC算法进行空间谱估计。

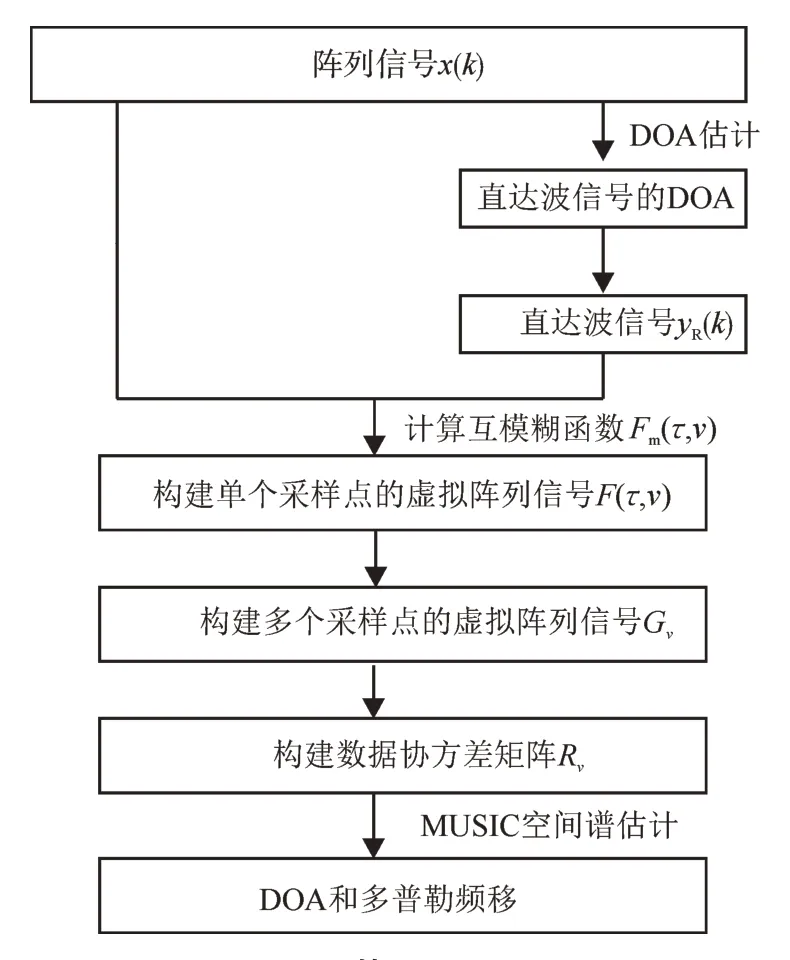
图1 算法流程图Fig.1 Flowchart of algorithm

3 仿真分析

3.1 FM辐射源信号

以采样频率为44.1 kHz从一段语音信号中截取时间为2 s的语音信号，将此语音信号作为基带信号进行FM调制，将此调制信号进行下变频，下变频后的采样率为300 kHz。图2（a）和图2（b）分别为经过下变频后2 s时长的FM信号的功率谱图和模糊函数图。其中P表示FM信号功率，f表示FM信号频率，SNR的值为κ，R表示距离差，ν表示多普勒频移，χ=20log10||A()

τ,ν。

图2 下变频后的FM信号：（a）功率谱图，（b）模糊函数图Fig.2 FM signal after down-conversion：（a）power spectrum chart，（b）ambiguity function diagram

3.2 阵列信号参数

接收阵列为M=16的均匀直线阵，假设阵列流型已知，并忽略耦合效应，2 s长的信号经天线阵接收后进行下变频，得到接收阵列信号。表1给出了直达波信号和5个散射波信号的仿真参数。用于扫描的多普勒频移区间从-40 Hz变化到40 Hz，步长为0.25 Hz，距离差区间从-100 km变化到100 km，步长为1 km。

表1 仿真参数Tab.1 Simulation parameters

3.3 散射波DOA估计

在第一个仿真例子中，使用本文提出的方法，即步骤1～4，计算DOA-多普勒图。如图3所示，图3（a）结果表明：1）在DOA为30°时出现一条“脊线”，贯穿整个多普勒频移区间。2）“脊线”的峰值表示多普勒频移为0 Hz和DOA为30°的直达波信号。3）在图3（a）中可观测到5个以上具有不同的DOA和对应的多普勒频移的峰。

图3（b）给出的是移除直达波信号所在区域后的DOA-多普勒频移图，可清晰地观察到5个峰值，分别对应于5个散射波信号。其中SNR的值为-40 dB的散射波信号3的DOA也被成功检测到。

图3 DOA-多普勒频移图：（a）所有角度，（b）部分角度Fig.3 DOA-Doppler-shift spectra：（a）all directions，（b）some directions

3.4 性能对比

为了与其他方法进行性能比较，将二维的DOA-多普勒图沿着多普勒维投影成一维的空间谱。其中ξ=10log10[P(θ,νFix)]。

图4（a）给出的是低信噪比情况下的3种算法性能比较图，从图4（a）中可以看到MUSIC算法、OPM-LP算法、RD-ASP算法在低信噪比情况下都能够分辨直达波和5个散射波信号的DOA。

图4（b）给出的是极低信噪比情况下的3种算法性能比较图，从图4（b）中可以观察到OPM-LP和MUSIC均不能分辨极低SNR的散射波，而本文提出的RD-ASP方法能够清晰地分辨5个散射波的DOA。

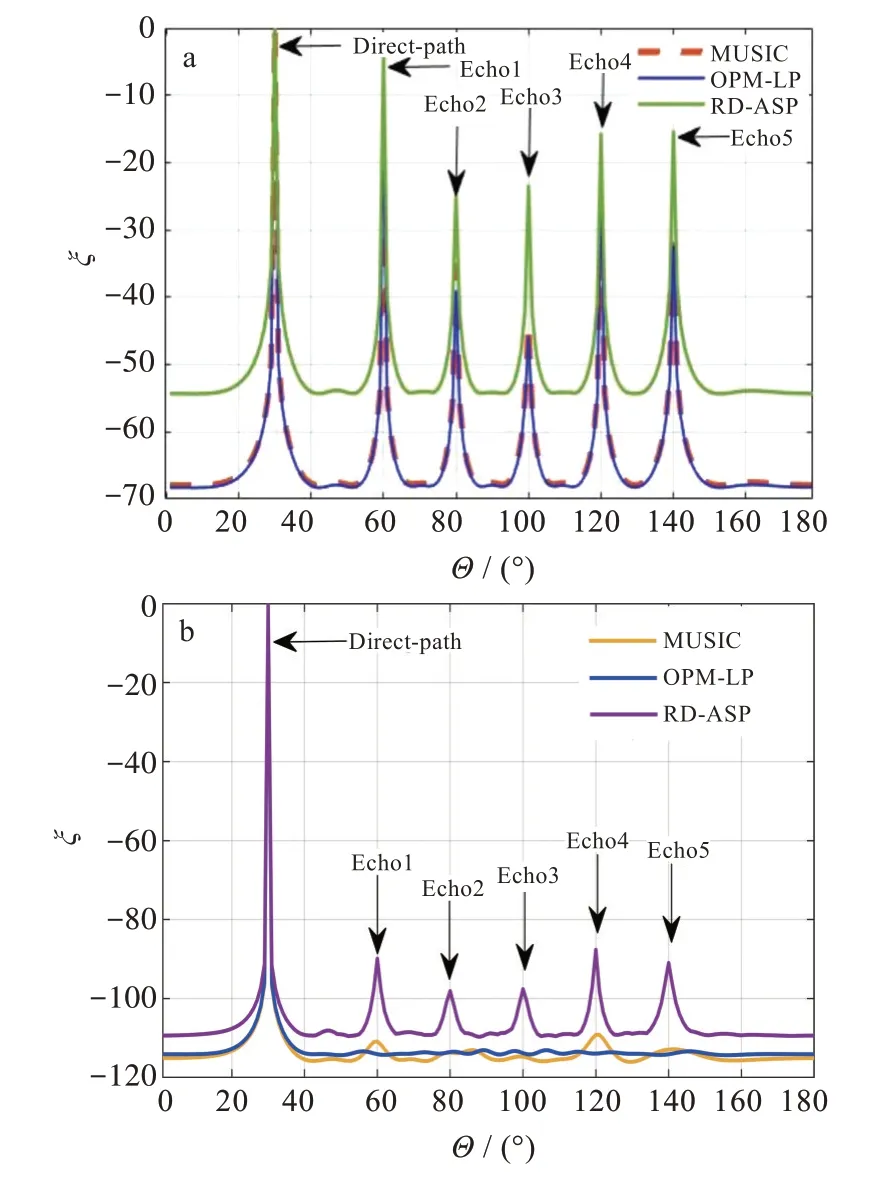
图4 3种算法的性能比较：（a）低信噪比，（b）极低信噪比Fig.4 Performance comparison of threealgorithms：（a）low signal-to-noiseratio，（b）extremely low signal-to-noiseratio

4 结 论

本文提出了一种距离多普勒域阵列信号处理方法，用于估计FM外辐射源雷达散射波信号的DOA。通过计算直达波信号与天线各个阵元接收信号的互模糊函数，然后抽取数据组成多个采样点的虚拟阵列信号。理论分析表明期望散射波信号在虚拟阵列信号中被显著增强，接下来可使用MUSIC算法估计散射波信号的DOA。仿真结果表明，本文所提出的方法能够在强直达波干扰情况下成功估计极低信噪比散射波的DOA，及其对应的多普勒频率。