High speed ghost imaging based on a heuristic algorithm and deep learning∗
Yi-Yi Huang(黄祎祎) Chen Ou-Yang(欧阳琛)Ke Fang(方可) Yu-Feng Dong(董玉峰)Jie Zhang(张杰) Li-Ming Chen(陈黎明) and Ling-An Wu(吴令安)
1Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China
2University of Chinese Academy of Sciences,Beijing 100049,China
3IFSA Collaborative Innovation Center and School of Physics and Astronomy,Shanghai Jiao Tong University,Shanghai 200240,China
4College of Engineering Physics,Shenzhen Technology University,Shenzhen 518118,China
Keywords: high speed computational ghost imaging,heuristic algorithm,deep learning
1. Introduction
Ghost imaging(GI),an unconventional imaging method,has received increased attention over the past few decades. In GI,image reconstruction is achieved by the correlation of two beams: the object beam and the reference beam. The former interacts with the object and is collected by a single-pixel bucket detector,while the latter never interacts with the object but is recorded by a high-spatial-resolution detector. GI was first demonstrated by using entangled photon pairs,[1]but later it was discovered that GI can be achieved by other sources with associated properties. Besides visible light,[2,3]now it has been demonstrated with x-rays[4,5]and even various particle sources such as electrons,[6]atoms,[7]and neutrons.[8]If the spatial speckle distribution of the reference beam can be precalibrated or preset, by using, for example, a spatial light modulator (SLM), then GI can be computed by the known modulation patterns and the corresponding signals acquired by the bucket detector. This scheme is known as computational ghost imaging(CGI),[9,10]and is particularly suitable for lowlight environments,[11]multispectral imaging,[12]information security,[13,14]remote sensing,[15,16]and other practical applications.
Even though ghost imaging has made great progress and extended into many related fields, imaging speed is still not satisfactory. In discrete measurements of CGI, according to the Nyquist–Shannon sampling theorem,[17]the number of modulation patternsMused to illuminate the object image should be at least equal to the total number of speckle pixelsN. To obtain high-resolution images,Mshould be as large as possible. In practice,however,the sequential display of a large set of illumination patterns by the SLM is timeconsuming due to its low frame rate,[18]and a largerMdemands more imaging time. Effort has been made to improve the imaging speed,such as by multiplexing the SLM,[19]or replacing it with a programmable light emitting diode array.[20]Another approach is to use efficient imaging algorithms to reduce the number of sampling exposures, for example, by using highly incoherent modulating patterns, e.g.,the reordering of Hadamard bases,[21–25]or using compressed sensing(CS)[26–28]and other iterative algorithms.[29–31]Compressed sensing can certainly reduce the sampling rate greatly and thus reduce the imaging time, but it requires a large amount of computation,which then requires long signal processing time,so the ultimate imaging speed is still limited. Recently, deep learning has been proposed to solve inverse problems in optical imaging[8,32–37]and has demonstrated better performance than the basic correlation algorithm or CS,when there is a sufficient number of training samples,especially at low sampling ratesβ=M/N,β ≤1. It can greatly improve the efficiency of data collection and has significant potential in practical applications.
Most previous works on GI have been concerned with static targets,but in practical remote sensing applications there is usually relative motion between the imaging system and the target, and imaging a moving target is much more meaningful.Although Ref.[23]described a Hadamard basis reordering method to realize real-time video imaging,it was not designed for moving objects and did not use the motion characteristics to shorten the modulation process and sampling time. In our work,we find that the imaging speed can be greatly improved within a certain range by using a condensed mask based on a Hadamard basis and overlapping sampling scheme,as we will explain below. For simplicity, we will discuss a simple scenario in which an object moves in a straight line across the field of view of the bucket detector with a constant unknown speed relative to the illumination patterns.
This paper is organized as follows. The basic principle of our overlapping sampling scheme and generation of the condensed illumination patterns will be described in Section 2.The neural network based scheme for high-speed deep learning GI(DLGI)will be presented in Section 3,and the simulation results will be shown in Section 4. The conclusion is in Section 5.
2. Generation of the illumination patterns
Our dynamic overlapping sampling scheme is based on illumination patterns designed by a heuristic algorithm. We first analyze the limits of the imaging speed of the dynamic GI,then design our condensed overlapping matrix mask. Next, a heuristic algorithm is used to minimize losses and redundancy of information in optimizing the matrices. Finally, we verify that the condensed matrices are much better than the random matrices.
2.1. Strategy for dynamic ghost imaging
The scheme of CGI for a moving-object is shown in Fig.1(a). For simplicity,we focus on two-dimensional imaging in the (x,y) plane, and assume that the object is just in front of the mask moving along thexdirection with constant velocityvobj. We consider a mask composed of a series ofMmatrices, aligned in a row, each matrix consisting of, for example,32×32 pixel patterns. In traditional CGI,each matrix would be illuminated in sequence one by one, and the total length of the mask would be 32M. However, we contract the mask in our dynamic CGI scheme,so that the matrices overlap horizontally in thexdirection, with each consecutive matrix overlapping 31 pixel columns with the previous one;the total length of the mask is thus only (M+31) pixels. The beam from a light source is expanded to illuminate the object and the entire width of the modulation mask, and is then focused by a lens onto the bucket detector.
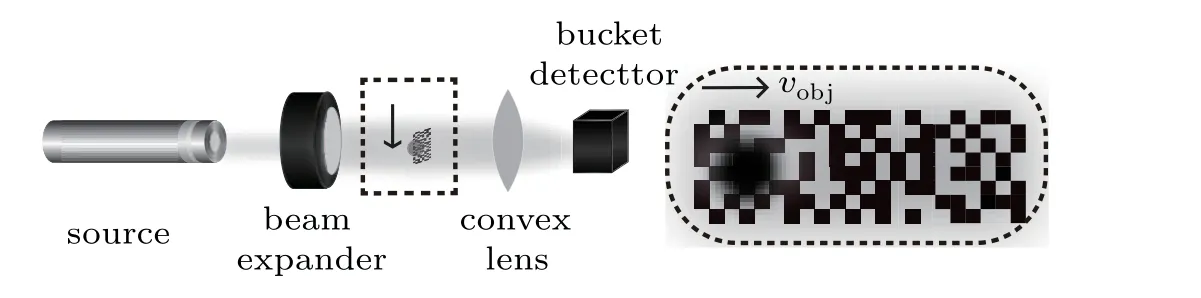
Fig. 1. CGI scheme of high-speed GI for a moving object. The black arrows represent the direction of motion of the object, which has a velocity vobj. Inset:enlargement of the dashed box,showing the position of the object relative to the mask.
If the object is moving across a static illumination patternI(x,y)with velocityvobj,its relative motion can be used to map the spatial information of the object into a 1D train of temporal signals. The signals are collected by a bucket detector at a sampling frequencyfs, and can be mathematically described as
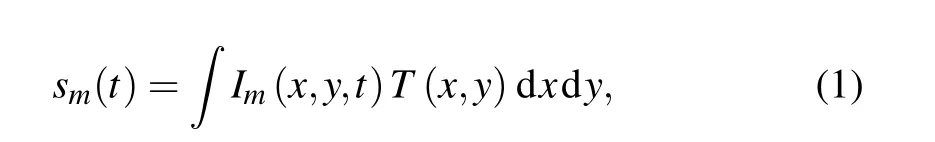
whereImis the pattern of them-th matrix,m=1,2,...,M,andT(x,y)is the transmissivity function of the object.
The image of the object is recovered from the correlation of the photon counts collected by the bucket detector with the spatial distribution of the modulation matrices through
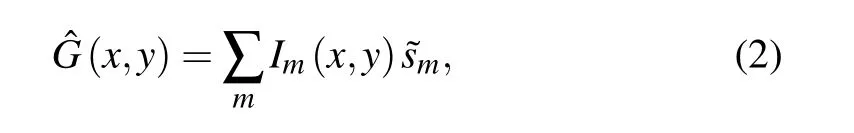
According to Rayleigh’s criterion, the images of two nearby points are indistinguishable when the center of the point spread function of one of the points falls on the first minimum of that of the other point. When the quasistatic approximation is employed,the ghost imaging has an important property. It is insensitive to an object’s weak dithering if its dithering amplitude is less thanlc, wherelcis the transverse coherent length of the light source. For a detector sampling frequency offs=1/ts,wheretsis the duration of a single exposure,the movement of the object can be considered indistinguishable if the distance travelled through during the timetsof one exposure is less thanlc,and the object can be considered to be stationary during the process. The maximum speedvmaxof the object for the quasistatic approximation to be valid[39]is
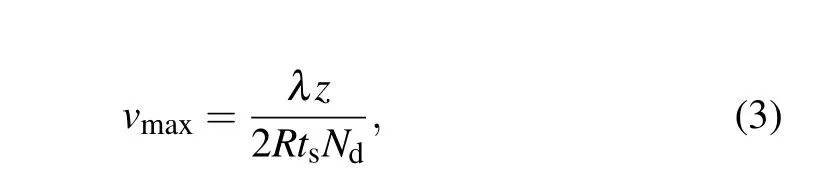
whereλis the central wavelength of the light,zthe distance between the target and mask,Rthe size of the smallest detail of the target, andNdthe minimum number of exposures required for the joint detection. Suppose that the total length of the illumination mask isL,then the shortest time required for sampling all the matrix patterns should beL/vmax. Obviously,the total imaging time required can be greatly decreased by shorteningL,increasing the sampling frequency,and reducing the required number of exposures. Note thatlcmust be much smaller than the minimum sizeµof the illumination pixels,in which case the resolution of the imaging system isµ.
2.2. Generation of the condensed overlapping matrix mask
In traditional GI,[5,8,39]the method shown in Fig. 2(a),which is called independent sampling,exposes each illumination pattern independently and sequentially. In this case,a set of orthogonal normalized Hadamard matrices can be used to obtain high quality images with a lower sampling rate, compared with random speckle patterns. In our work,we shorten the total lengthLand the imaging time of the illumination patterns through the overlapping sampling method as shown in Fig. 2(b), where the distance between the adjacent mask patterns is one pixel column, i.e., after each sampling the target has moved through one pixel column, or equivalently, the illumination mask has moved one pixel relative to the object before the next sampling. Assuming that the area of the target isP×Ppixels,then the lengthLolof the overlap between them-th and then-th patterns isP −(n −m) pixels, whenP >(n −m)>0. For complete independent sampling with a Hadamard mask,P2exposures would be required and the total lengthLof the illumination mask would beP3. However,for overlapping sampling,the length would be onlyP2+P−1,which means that the imaging time can be shortened nearlyPtimes. On the other hand, in this case the adjacent illumination patterns are highly overlapping, which means that there will be some redundant information and inherent noise,so the quality of the recovered image is degraded for the same number of samplings. Moreover,for random illumination patterns,overlapped sampling will perform even worse. To overcome this we use a heuristic algorithm to create a new condensed modulation maskMHCbased on the original Hadamard matrices,which can greatly improve the quality of the recovered image.

Fig. 2. Sampling methods. (a) Independent sampling: each matrix is completely independent of other adjacent matrices. (b) Overlapped sampling:each sampling covers a matrix that is positioned one pixel to the right of the former matrix,thus adjacent illumination patterns in this case are highly overlapping.
The basic idea of our overlap contraction is to make each illumination pattern as similar as possible to one of a set of Hadamard matrices, which means we need to rerank the Hadamard matrices. We thus run a program to minimize the difference between each illumination pattern and its corresponding Hadamard matrix,as follows:
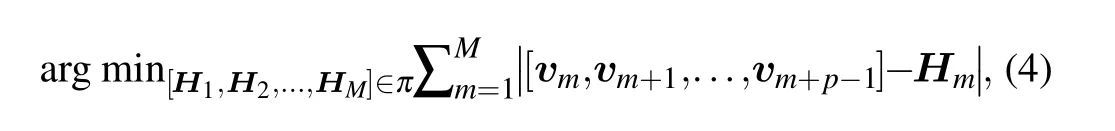
whereHmis them-th Hadamard matrix,m=1,2,...,M,viis thei-th column of the condensed mask,i=1,2,...,M+P−1,πis the set ofMHadamard matrices of different sequences,and[vm,vm+1,...,vm+P−1]represents an illumination pattern corresponding toHm. It can be proved that Eq.(4)has an exact solution when the sequence of the Hadamard matrices is fixed. When we rearrange the matrices and then overlap them in the way shown in Fig.2(b),Eq.(4)can be simplified as
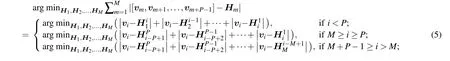
whereHkmrepresents thekth column of them-th Hadamard matrix. Since the sequence ofHmis known, everyHkmis known, thenviof the condensed mask can be found by calculating the mean value of a given pixel in all the overlapping layers. From Eq. (5) we can obtain a precise matrix where the value of each pixel lies between 0 and 1. However, what we ultimately want is a binary matrix,so to binarize the condensed matrixv, when the mean value is greater or less than 0.5,the pixel value is set as 1 or 0,respectively;when the mean value is equal to 0.5,the value is set as 0 or 1 randomly with a probability of 0.5.
In order to reduce the loss of information, the mean of each pixel value should be as close to 0 or 1 as possible.However, there areP2! ways to arrange the Hadamard matrix,which is an NP-hard(non-deterministic polynomial-time hard)problem. For overlapped sampling,the more similar the overlapping part of adjacent matrices, the less information is lost. Since it is impossible to enumerate all the possible arrangements of the Hadamard matrices, we only consider two adjacent matrices, and arrange the matrices by the principle that the overlapping portions of two adjacent matrices should be as similar as possible,which is a heuristic algorithm.
We try two ways of rearrangement,random and heuristic,to form two new condensed matrices,MRCandMHC, respectively. In the following,we will demonstrate through simulation results that the heuristic sorting is far more effective than the random one.
2.3. GI reconstruction using traditional and condensed masks
In traditional GI,the image is reconstructed from the correlation of the bucket intensity fluctuations with the illumination patterns,as given in Eq.(2).
In CSGI,we can use the orthogonal matching pursuit algorithm (OMP)[40]to solve the following optimization problem:

wheregis the time signal of the vector,Ithe matrix reshaped fromIm,iis a vector reshaped from the image of the input object,and‖•‖represents theL2norm.
To compare the images obtained with various modulation matrices through CS,we have selected a binary digital object(Fig. 3(a)), and examined how the number of exposures,M,affects the reconstructed image. For the three different cases ofMequal to 1024, 512 and 256, i.e., sampling ratios ofβ=M/1024 equal to 100%,50%,and 25%,respectively,the corresponding images are shown in the first,second,and third columns of Fig.3(b). The first and second rows were obtained by using the heuristic and random condensed matrices, while the third row from random matrices. We can see that when the sampling rate is reduced to 50%, the heuristic condensed matrices perform better than the random or random condensed matrices. However,when the sampling rate is further reduced(β <50%), no matter which mask is used the images are always fuzzy.

Fig. 3. (a) Digital object; (b) GI images recovered with sampling rates of 100%,50%,and 25%for different matrices through compressive sensing.
For an object with binary transmission,the image quality of the image can be quantified using the contrast-to-noise ratio(CNR),which is defined as[41]
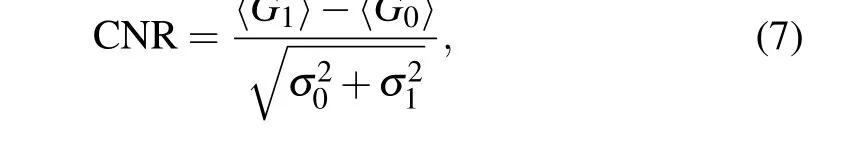
where〈G0〉and〈G1〉are the ensemble averages of the ghost image signal at any pixel where the transmission is and 1,respectively,andσ20andσ21are the corresponding variances.
For a more qualitative comparison between the three types of matrices, we plot the CNR of the different reconstruction methods as a function of sampling rate in Fig. 4. It is evident that the heuristic condensed mask always improves the CNR, even at low sampling rates, which shows that the heuristic condensed matrices can greatly reduce the inherent noise, with much better performance than random matrices.To further reduce the inherent noise,we can use a deep learning algorithm as will be discussed below.
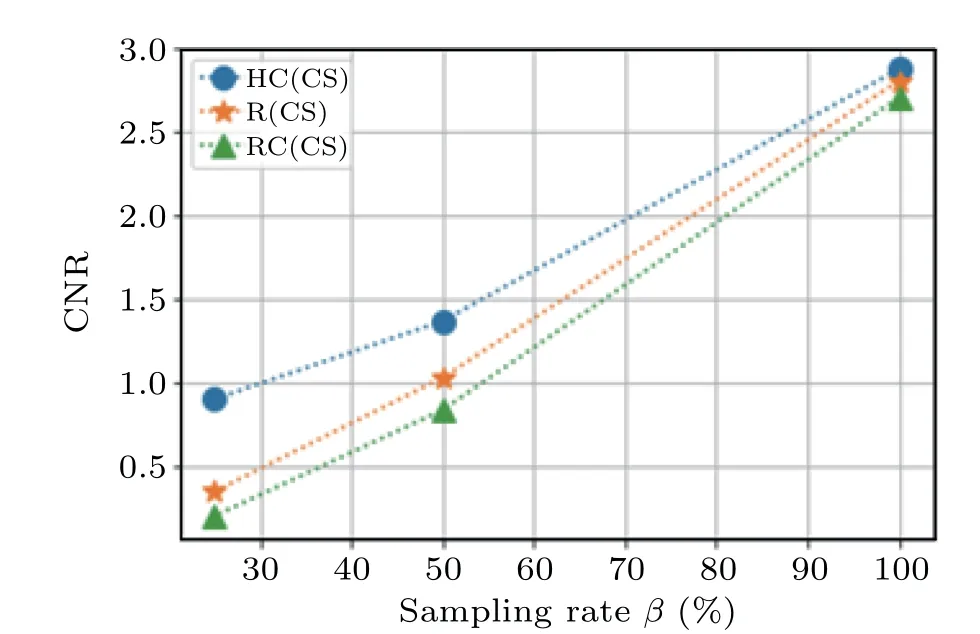
Fig.4. The CNR of CS(dashed lines)vs. sampling rate using heuristic condensed(HC,dots),random condensed(RC,triangles),and random(R,stars)matrices modulation.
3. Learning-based algorithm
The method we propose here employs a deep neural network to reconstruct the ghost image, through the following expression:



3.1. Design of a convolutional neural network
We propose here a neural network,the structure of which is shown in Fig.5. The input of the network is the normalized bucket signal of lengthMand the pre-designed condensed matrices,while the output should be the image of the object. Due to the multiple overlapping of adjacent illumination patterns,there will be some correlation between the one-dimensional bucket signals,that is,the value of a given bucket signal will be related to the previous and subsequent values. Therefore, we use the bi-directional long short-term memory (LSTM) layer scheme[43–45]to learn the correlation between time-dependent bucket signalsS(t), and then it is combined with the heuristic condensed matrices and LSTM output to obtain the preliminary image information. Next, the convolutional neural network (CNN)[46–48]commonly used in computer vision is used for noise reduction processing. Inspired by the YOLOv4 algorithm,[48]we have used CSPDarknetlike as the backbone to reduce the risk of the gradient disappearing. In addition,we have used 3 independent paths, each of which has an upsampling layer to up-sample the incoming feature map, creating 3 independent data flows. Each data flow is then sent to a set of identical residual blocks,which are used to extract feature maps at different scales. Following the residual layers, there are up-sampling layers that can restore the size of the feature maps back to 32×32, after which the 3 paths are concatenated into one. The concatenated image then passes through a residual block to yield the reconstructed image. In Fig.5,a digit in the format of(W,H,C)is placed in each layer to denote the size of its output. We also use dropout layers and batch-normalization layers to prevent overfitting.

Fig. 5. Proposed neural network architecture to learn the GI image restoration from the pre-designed illumination patterns and measured intensities.
3.2. Network training
As mentioned before,the training of the network is a process to optimize the values of the parameters in the set Θ.These parameters include the weighting factors and bias connecting the neurons in two neighboring layers. In the case of supervised learning as in our study,we need a substantial collection of known images and their bucket signals as constraints to iteratively optimize the neural network so that it can reconstruct an expected image from a bucket signal in the test set.In the training process,we define the loss functionL(G,learn)as the mean square error between the reconstructed image and the corresponding known image(ground truth)
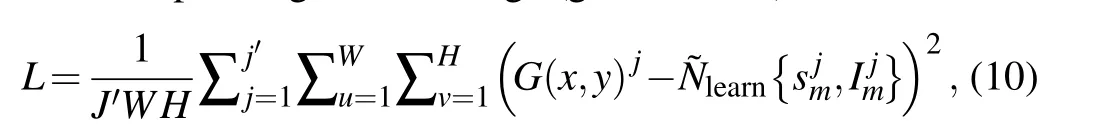
whereWandHare the width and height of the reconstructed image,respectively,andJ'=64 is the mini-batch size. In our simulation, we have used 20000 images for training from the MNIST handwritten digit databases,and binarized and resized these images to 32×32 so thatN=1024. We have adopted the Adam optimizer to optimize the weights and set the learning rate to 0.1. The epoch was 600. The program was implemented in Pytorch 1.3.1. In our study, we have considered 5 different cases for sampling ratios ofβ=100%, 50%, 25%,12.5%,and 6.25%.
4. Results and discussion
For comparison, we have plotted the images of the numeral 2 retrieved by CSGI and DLGI withβ=100%, 50%,25%,12.5%,and 6.25%. From the results shown in Fig.6(b)it can be seen that,compared with CSGI,deep learning is able to reconstruct the image (upper row) much better even at a very low sampling rate. To examine the generalization of the trained neural network model,we have also used it to recover the images of 2000 targets and they are different from those in the training set.As an example,Fig.6(c)shows the simulation results of 10 of the 2000 targets, numerals 0 to 9, and proves that the proposed method can approximately reconstruct the image even at a sampling rate of 6.25%, which means that the total lengthLof all the illumination patterns can be further shortened to reduce the imaging time. For example,if the size of the recovered image is 32×32 pixels,the required sampling timetsis on the order of microseconds and the resolution is 50 µm, so from Eq. (2) we can estimate the total imaging time to be on the order of milliseconds. Moreover, a plot of the CNR of CSGI and DLGI as a function of sampling ratio is shown in Fig.7. As expected,traditional correlation-based CGI fares the worst, while DLGI has the best overall performance,which is consistent with the results shown in Fig.6(b).

Fig.6. (a)Digital object. (b)Images recovered with different sampling rates β (shown at the top)using DLGI and CSGI.(c)Different images recovered by DLGI for a sampling rate of β =6.25%;upper row: recovered images;lower row: digital objects.

Fig.7. The CNR of GI(dots),CSGI(stars),and DLGI(diamonds)vs. sampling rate β.
5. Conclusion
We have proposed an overlapping sampling scheme for the ghost imaging of fast moving targets,which can greatly reduce the imaging time. When the illumination area is limited,this method can shorten the total length of the illumination mask as well as increase the field of view. Our newly designed heuristic condensed mask can greatly reduce the redundant information and inherent noise, with much better performance than random matrices. Moreover, deep learning can further improve the image quality even at very low sampling rates. To reduce the imaging time even further, we can envisage using multiple singlepixel cameras in parallel so that high resolution images can be obtained over a wide field of view in even shorter time.
In conclusion,our condensed matrix GI scheme may enjoy potential practical applications in wide-ranging fields such as target tracking,biomedical analysis,and autonomous vehicle technology.
- Chinese Physics B的其它文章
- Coarse-grained simulations on interactions between spectrins and phase-separated lipid bilayers∗
- Constraints on the kinetic energy of type-Ic supernova explosion from young PSR J1906+0746 in a double neutron star candidate∗
- Computational model investigating the effect of magnetic field on neural–astrocyte microcircuit∗
- Gas sensor using gold doped copper oxide nanostructured thin films as modified cladding fiber
- Exact explicit solitary wave and periodic wave solutions and their dynamical behaviors for the Schamel–Korteweg–de Vries equation∗
- Suppression of ferroresonance using passive memristor emulator

