基于NSGA-II 遗传算法的智能飞行器航迹快速规划

张伟聪，韩伟娜，白雪丽，韩 旭，任 宽，田丽丽

（1.北华航天工业学院机电工程学院；2.北华航天工业学院遥感信息工程学院，河北廊坊 065000）

0 引言

现代飞行器技术经过多年发展，结构和操作越来越复杂，在安全突防任务难度愈来愈大的情况下，智能飞行器航迹规划占有重要地位。快速准确的航迹规划可有效节约能源提高效率，其研究具有重大意义。

智能飞行器航迹规划通常存在约束工况比较复杂和优化规模较大等问题时，一般情形会采用启发式智能优化算法，如蚁群算法、粒子群算法、模拟退火算法、遗传算法等［1］。Patcher 等［2］讨论了路径规划问题中的关键优化技术及其复杂性；Dong 等［3］、Zhang 等［4］、Nikolos 等［5］系统研究了路径规划中进化算法的优化原理；Wu 等［6］最早将遗传算法应用于航行器的路径规划问题；朱海斌等［7］引入量子遗传算法克服了遗传算法早熟问题；李文广等［8］改进转弯航迹规划算法，降低了15%路径。近年有关智能飞行器航迹规划优化研究主要集中于对启发式智能优化算法进行改进［9-13］。

传统的遗传算法在搜索空间和目标函数方面要求不高，具有范围广、鲁棒性高以及全局搜索能力较强的优点，但是容易陷入局部求解，且收敛结果易反复。非支配排序遗传算法（NSGA）经过个体支配关系的分层，在速度上有了很大提升。本文利用带精英策略的非支配排序遗传算法（NSGA-II）应用于智能飞行器的航迹规划问题中，主要解决NSGA 的排序速度慢以及找到最优解时收敛容易反复的缺陷。

1 航迹规划问题

智能飞行器航迹规划指在环境及战场危险情况如飞行时间、燃油消耗等全方位约束条件下，找到一条自给定起点至目标点的优质飞行轨迹，这是一个典型的多目标优化问题［14］。

复杂环境下的航迹快速规划是智能飞行器控制课题的重要组成部分，飞行器的定位系统往往由于其自身结构限制无法做到精准定位，当误差累积达到一定程度会导致整体任务失败。

1.1 航迹规划基本要求

假设智能飞行器飞行区域中出发点为A 点，目的地为B 点，其航迹约束如下：

（1）飞行器在空间飞行过程中需要实时定位，其定位误差包括垂直误差和水平误差。飞机每飞行1m，垂直误差和水平误差将增加δ个专用单位（以下简称单位），到达终点时垂直误差和水平误差均小于θ个单位。为简化问题，假设当垂直误差和水平误差均小于θ个单位时飞行器仍可按照规划路径飞行。

（2）飞行器在飞行过程中需要对定位误差进行校正。飞行区域中存在一些安全位置（称之为校正点）可用于误差校正，当飞行器到达校正点即可根据该位置的误差校正类型进行误差校正。校正垂直和水平误差的位置可根据地形在航迹规划前确定。若垂直误差、水平误差都能得到及时校正，则飞行器可以按照预定航线飞行，通过若干个校正点进行误差校正后最终到达目的地。

（3）在出发地A 点，飞行器的垂直和水平误差为0；飞行器在垂直误差校正点校正后，其垂直误差将变成0，水平误差保持不变；飞行器在水平误差校正后，其水平误差将变成0，垂直误差保持不变；飞行器在垂直误差不大于α1个单位、水平误差不大于α2个单位时才能进行垂直误差校正；在垂直误差不大于β1个单位、水平误差不大于β2个单位时才能进行水平误差校正。

（4）飞行器在转弯时受到结构和控制系统限制，无法完成即时转弯，最小转弯半径设为200m。

1.2 智能飞行器航迹问题

本文研究智能飞行器的航迹规划是根据2019 年全国研究生数学建模竞赛F 题中的问题二改编［15］。综合考虑优化目标，要求航迹长度尽可能小，在校正区域进行校正的次数尽可能少。绘制出数据集的航迹规划，并求出飞行器从起点出发经过误差校正点的编号及校正前误差，讨论算法的有效性。

2 智能飞行器航迹规划

2.1 航迹规划数学模型

在智能飞行器起点A 到终点B 的航迹规划中，根据问题要求假设飞行器从一个校正节点到另一个校正节点之间始终进行匀速直线运动，记C=[c1,c2,c3...,ci,...,cn]为校正点集，n 为校正点个数；U=[u1,u2,u3...,ui,...,um]为水平校正集，V=[v1,v2,v3...,vi,...,vQ]为垂直校正集，m 为水平校正点个数，Q 为垂直校正点个数。

智能飞行器飞行路程目标函数为：

飞行器经过校正点的目标函数为：

式中：

上一个点到下一个点的路程长度为：

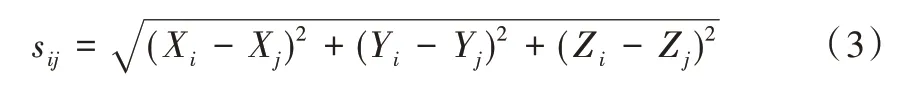
基于基本要求的约束条件如下：

其中Pij是两个校正点之间的误差增量。

对最小转弯半径约束为：

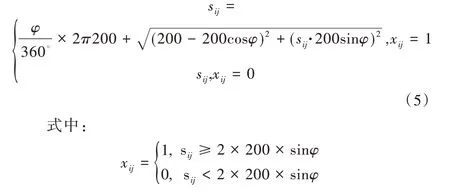
2.2 NSGA-II 算法求解过程

NSGA-II 算法的核心是父代与子代的合并，基于传统遗传算法进行基本操作。

（1）基于NSGA-II 遗传算法的智能飞行器航迹规划算法流程如图1 所示。

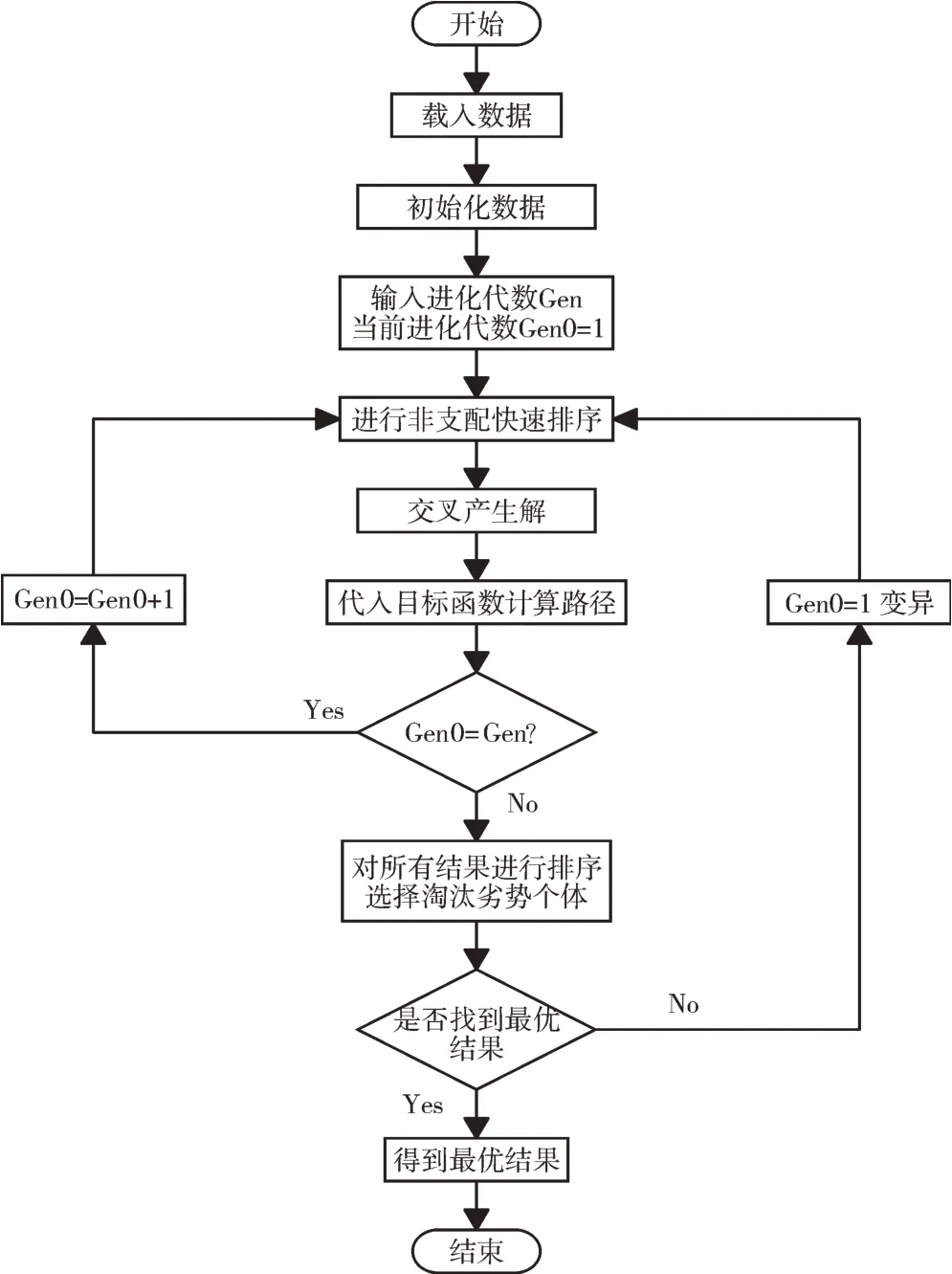
Fig.1 Route planning flow of intelligent vehicle based on NSGA-II genetic algorithm图1 基于NSGA-II 遗传算法的智能飞行器规划航迹流程

（2）智能飞行器航迹规划算法添加以下约束：①当前后两个校正节点距离超过最大误差和单位距离误差的比值时，解无效，生成的下一个节点间距离必须小于最大误差和单位距离误差的比值；②水平校正点和垂直校正点需分开进行约束，且节点到达下一个校正后才能校正误差，利用当前误差余量对下一个解的距离进行约束；③每个节点只能用一次，节点到达B 点附近就可尝试直接连接B 点。

（3）产生的新解带入目标函数找到优化目标下的最佳航迹：①利用交叉和变异因子产生新解；②输出可行解，得出最优航迹；③记录遍历的校正点，得出最优航迹对应的最优校正点。

3 仿真结果

根据数据集中附件1 的数据，利用NSGA-II 算法将数据带入约束进行迭代，本次迭代次数为30 次，得出对应的智能飞行器最优航迹规划如图2 所示，其中A 点代表起点，B 点代表终点，其它点分别是垂直和水平校正点。

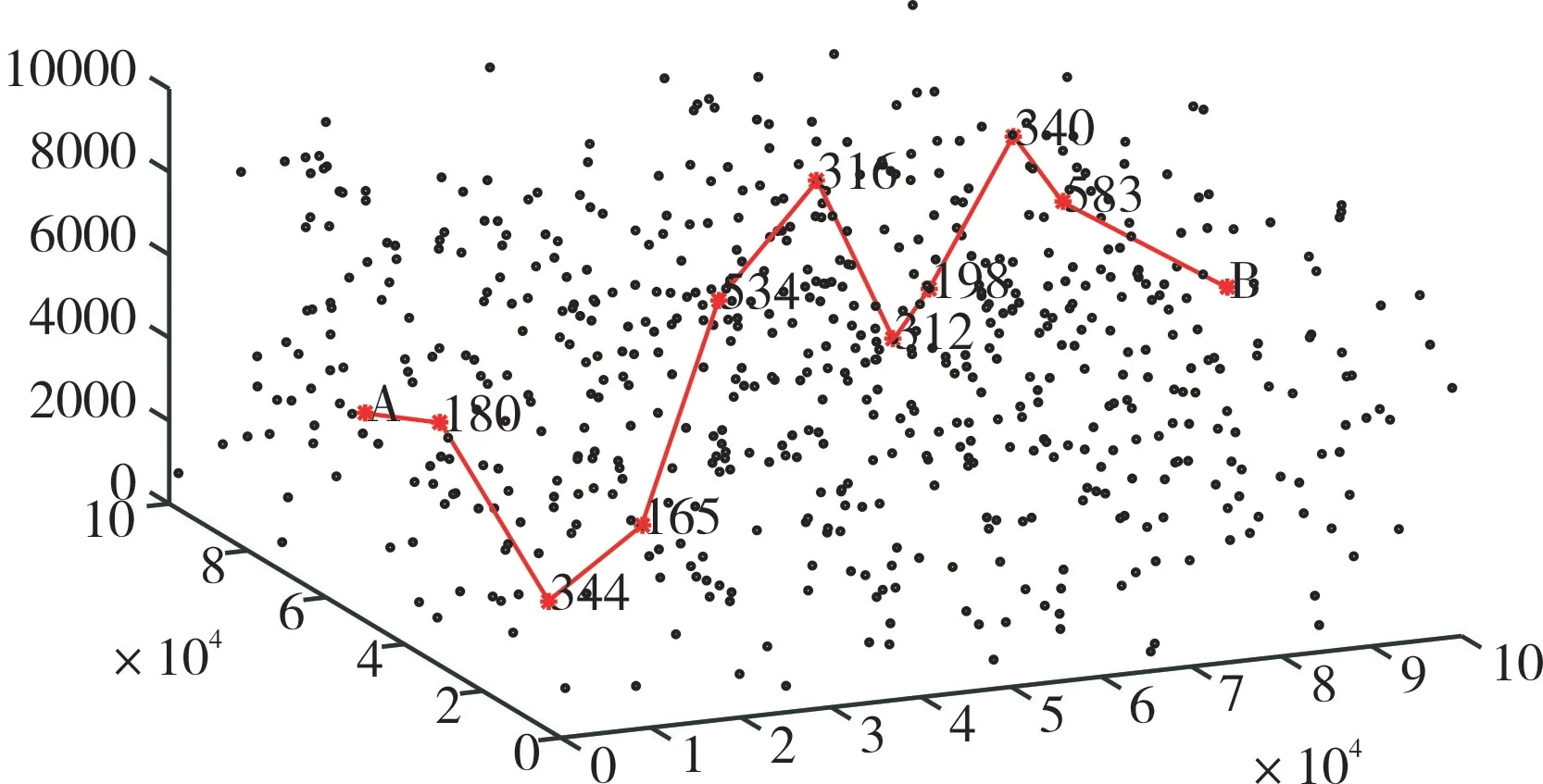
Fig.2 NSGA-II genetic algorithm for optimal path planning of intelligent vehicle图2 NSGA-II 遗传算法智能飞行器规划最优航迹

通过NSGA-II 算法综合考虑实际情况，得到一条从起点A 到终点B 的最优路径长度、最佳校正节点数的航迹规划：起 点A→180→344→165→534→316→312→198→340→583→终点B。根据算法得到多约束规划的值分别为：

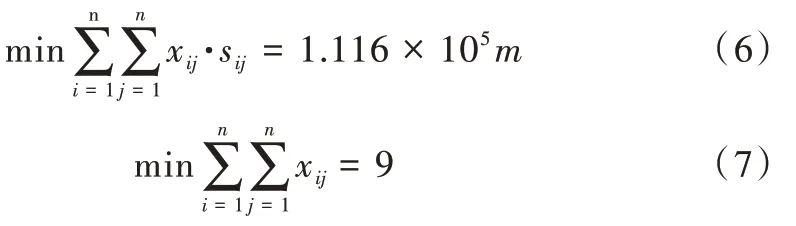
从图2 得到智能飞行器从起点A 出发经过误差校正点的编号及校正前的误差结果如表1 所示。

Table 1 Route planning results表1 航迹规划结果

与NSGA 算法相比，NSGA-II 算法能实现快速、准确的搜索性能。分析智能飞行器航迹规划总路径和校正次数后发现，NSGA-II 算法相对于NSGA 算法收敛速度快了一倍，且最优结果不易反复。在同时迭代50 次后，NSGA-II算法与NSGA 算法的对比结果如图3 和图4 所示。

Fig.3 Total distance iterative curve of intelligent vehicle based on two genetic algorithms图3 两种遗传算法智能飞行器总路程迭代曲线

Fig.4 Two kinds of genetic algorithms for intelligent vehicle calibration图4 两种遗传算法智能飞行器校正次数迭曲线

图中虚线代表采用NSGA 算法进行规划的结果迭代情况，实线代表采用NSGA-II 算法进行规划的结果迭代情况。从图中可以很容易看出，NSGA-II 算法避免了NSGA 算法的一些缺点，可以更准确快速地获得智能飞行器在满足约束条件下的最优轨迹，并且在找到最优轨迹时收敛不会出现局部反复。

4 结语

本文采用NSGA-II 算法进行了多约束条件下智能飞行器的航迹规划。实验表明该算法能快速且准确得出最优轨迹，解决了NSGA 算法最终结果不收敛的问题。值得指出的是，改进的遗传算法越来越多，无疑对解决智能飞行器的航迹规划问题提供了保障，但同时每次都需要通过对比实验进行改进，在很大程度上限制了遗传算法的发展速度。